EAM_Dynamo_HepburnAckland_2008_FeC__MO_143977152728_005
EAM_Dynamo_HepburnAckland_2008_FeC__MO_143977152728_005
| Title
A single sentence description.
|
EAM potential (LAMMPS cubic hermite tabulation) for the FeC system developed by Ackland and Hepburn (2008) v005 |
|---|---|
| Description
A short description of the Model describing its key features including for example: type of model (pair potential, 3-body potential, EAM, etc.), modeled species (Ac, Ag, ..., Zr), intended purpose, origin, and so on.
|
Potential model for iron-carbon incorporation covalent bonding effects. At time of publication this was the only potential which binds properly to vacancies and NOT to interstitials. This gives it the right energetics in a dislocation core, and at a surface. Good clustering of C behavior and fct martensite. Solution energy -7.13eV, migration energy 0.89eV (i.e. diffuses more slowly than vacancies). Compatible with Ackland-Mendelev '04 iron. |
| Species
The supported atomic species.
| C, Fe |
| Disclaimer
A statement of applicability provided by the contributor, informing users of the intended use of this KIM Item.
|
Does not describe cementite. Does not describe Carbon. |
| Content Origin | http://www.ctcms.nist.gov/potentials/C.html |
| Contributor |
Graeme J. Ackland |
| Maintainer |
Graeme J. Ackland |
| Developer |
Derek J. Hepburn Graeme J. Ackland |
| Published on KIM | 2018 |
| How to Cite | Click here to download this citation in BibTeX format. |
| Citations
This panel presents information regarding the papers that have cited the interatomic potential (IP) whose page you are on. The OpenKIM machine learning based Deep Citation framework is used to determine whether the citing article actually used the IP in computations (denoted by "USED") or only provides it as a background citation (denoted by "NOT USED"). For more details on Deep Citation and how to work with this panel, click the documentation link at the top of the panel. The word cloud to the right is generated from the abstracts of IP principle source(s) (given below in "How to Cite") and the citing articles that were determined to have used the IP in order to provide users with a quick sense of the types of physical phenomena to which this IP is applied. The bar chart shows the number of articles that cited the IP per year. Each bar is divided into green (articles that USED the IP) and blue (articles that did NOT USE the IP). Users are encouraged to correct Deep Citation errors in determination by clicking the speech icon next to a citing article and providing updated information. This will be integrated into the next Deep Citation learning cycle, which occurs on a regular basis. OpenKIM acknowledges the support of the Allen Institute for AI through the Semantic Scholar project for providing citation information and full text of articles when available, which are used to train the Deep Citation ML algorithm. |
This panel provides information on past usage of this interatomic potential (IP) powered by the OpenKIM Deep Citation framework. The word cloud indicates typical applications of the potential. The bar chart shows citations per year of this IP (bars are divided into articles that used the IP (green) and those that did not (blue)). The complete list of articles that cited this IP is provided below along with the Deep Citation determination on usage. See the Deep Citation documentation for more information. 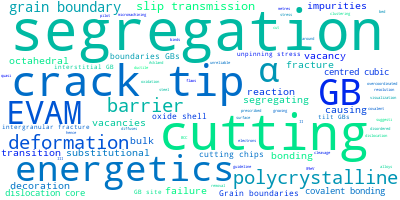
108 Citations (48 used)
Help us to determine which of the papers that cite this potential actually used it to perform calculations. If you know, click the .
USED (definite) S. Goel, F. D. Martinez, S. Chavoshi, N. Khatri, and C. Giusca, “Molecular dynamics simulation of the elliptical vibration-assisted machining of pure iron,” Journal of Micromanufacturing. 2018. link Times cited: 27 Abstract: It is well known that diamond wears out rapidly (within seve… read more USED (definite) C. Healy and G. Ackland, “Molecular dynamics simulations of compression–tension asymmetry in plasticity of Fe nanopillars,” Acta Materialia. 2014. link Times cited: 79 USED (definite) N. Rhodes, M. Tschopp, M. Tschopp, and K. Solanki, “Quantifying the energetics and length scales of carbon segregation to α-Fe symmetric tilt grain boundaries using atomistic simulations,” Modelling and Simulation in Materials Science and Engineering. 2012. link Times cited: 52 Abstract: Segregation of impurities to grain boundaries (GBs) plays an… read more USED (high confidence) B. Waters, D. S. Karls, I. Nikiforov, R. Elliott, E. Tadmor, and B. Runnels, “Automated determination of grain boundary energy and potential-dependence using the OpenKIM framework,” Computational Materials Science. 2022. link Times cited: 5 USED (high confidence) Z. Cheng and H. Wang, “A multi-grid sampling multi-scale method for crack initiation and propagation,” ArXiv. 2021. link Times cited: 2 USED (high confidence) L. Xiang, L. Liang, Y. Wang, Y. Chen, H. Wang, and L. Dai, “One-step annealing optimizes strength-ductility tradeoff in pearlitic steel wires,” Materials Science and Engineering: A. 2019. link Times cited: 21 USED (high confidence) I. Adlakha and K. Solanki, “Role of hydrogen on the incipient crack tip deformation behavior in α-Fe: An atomistic perspective,” Journal of Applied Physics. 2018. link Times cited: 16 Abstract: A crack tip in α-Fe presents a preferential trap site for hy… read more USED (high confidence) G. Aral, Y. Wang, S. Ogata, and A. Duin, “Effects of oxidation on tensile deformation of iron nanowires: Insights from reactive molecular dynamics simulations,” Journal of Applied Physics. 2016. link Times cited: 28 Abstract: The influence of oxidation on the mechanical properties of n… read more USED (high confidence) I. Adlakha and K. Solanki, “Critical assessment of hydrogen effects on the slip transmission across grain boundaries in α-Fe,” Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences. 2015. link Times cited: 25 Abstract: Grain boundaries (GBs) play a fundamental role in the streng… read more USED (high confidence) D. Terentyev, A. Bakaev, and E. Zhurkin, “Effect of carbon decoration on the absorption of 〈100〉 dislocation loops by dislocations in iron,” Journal of Physics: Condensed Matter. 2014. link Times cited: 11 Abstract: This work closes a series of molecular dynamics studies addr… read more USED (high confidence) M. Rajagopalan, M. Tschopp, and K. Solanki, “Grain Boundary Segregation of Interstitial and Substitutional Impurity Atoms in Alpha-Iron,” JOM. 2013. link Times cited: 81 USED (high confidence) V. Jansson and L. Malerba, “Simulation of the nanostructure evolution under irradiation in Fe-C alloys,” Journal of Nuclear Materials. 2013. link Times cited: 51 USED (low confidence) S. LYu, Y. Gao, A. Wang, and Y. Hu, “Research on Representative Volume Element Fex-Cy High-Temperature Mechanical Model Based on Response Surface Analysis,” Applied Sciences. 2023. link Times cited: 0 Abstract: In this research, a multi-scale representative volume elemen… read more USED (low confidence) K. Wang et al., “Multiscale Analysis of Wheel-Rail Rolling Contact Wear and Damage Mechanisms using Molecular Dynamics and Explicit Finite Elements,” Tribology International. 2023. link Times cited: 2 USED (low confidence) T. Xu, W. Wang, H. Jiang, and G. He, “Study on micro crack propagation mechanism of ferrite–pearlite gas transmission pipeline steel with lamellar structure,” Scientific Reports. 2022. link Times cited: 1 USED (low confidence) W. Liang, C.-he Jiang, K. Li, J. Zhang, and Z. Bi, “Effect of Graphene Wrinkle Degree on the Interfacial Behavior Between Iron and Graphene: Atomic Simulation,” Journal of Molecular Liquids. 2022. link Times cited: 0 USED (low confidence) Z. Song, X. Tang, X. Chen, T. Fu, H. Zheng, and S. Lu, “Nano-indentation and nano-scratching of pure nickel and NiTi shape memory alloy thin films: an atomic-scale simulation,” Thin Solid Films. 2021. link Times cited: 12 USED (low confidence) C.-he Jiang, K. Li, J. Zhang, M. Sun, and Z. Bi, “Structural characteristics of liquid iron with various carbon contents based on atomic simulation,” Journal of Molecular Liquids. 2021. link Times cited: 3 USED (low confidence) L. Wang et al., “Effect of interfacial bonding on dislocation strengthening in graphene nanosheet reinforced iron composite: A molecular dynamics study,” Computational Materials Science. 2021. link Times cited: 8 USED (low confidence) B. Zhang et al., “Atomic modeling of the segregation of vacancies on 111 dislocations in α-iron by diffusive molecular dynamics simulations,” Journal of Alloys and Compounds. 2020. link Times cited: 2 USED (low confidence) Á. A. Izquierdo-Sánchez, A. Oila, and A. Charles, “Atomistic simulation of tensile tests on iron and ferrite,” Materialia. 2020. link Times cited: 4 USED (low confidence) C.-he Jiang et al., “Molecular dynamics simulation study on the wetting behavior of liquid iron and graphite,” Journal of Molecular Liquids. 2020. link Times cited: 4 USED (low confidence) J. Li, H.-cai Xie, W.-qing Meng, X.-ming Zhang, W. Zhao, and G. Shi, “Evolution mechanism of subsurface defect structure in particle micro-cutting iron–carbon alloy process,” Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology. 2020. link Times cited: 10 Abstract: In order to explore the evolution mechanism of subsurface de… read more USED (low confidence) R. M. Gerasimov and P. Volegov, “Modeling of interaction of edge dislocations and microvoids using molecular dynamic approach.” 2020. link Times cited: 1 USED (low confidence) H. Qu et al., “Molecular Dynamics Simulation of Gas Pipeline Steel Based on LAMMPS Parallel Computing Platform,” DEStech Transactions on Computer Science and Engineering. 2019. link Times cited: 0 Abstract: Along with the advent of the fourth industrial revolution, t… read more USED (low confidence) H. Nguyen, C. Tran, G. Coman, H. Q. Nguyen, and V. Q. Dinh, “Thermodynamic properties of interstitial alloy FeC with BCC structure under pressure,” IOP Conference Series: Materials Science and Engineering. 2019. link Times cited: 1 Abstract: The analytic expressions for the thermodynamic quantities su… read more USED (low confidence) C. Tran, G. Coman, H. Q. Nguyen, H. T. Nguyen, and V. Q. Dinh, “The melting temperature of BCC perfect ternary alloy FeCrC under pressure,” IOP Conference Series: Materials Science and Engineering. 2019. link Times cited: 2 Abstract: The analytic expressions of the mean nearest neighbour dista… read more USED (low confidence) T. Wang, J. Du, and F. Liu, “Modeling Competitive Precipitations Among Iron Carbides During Low-Temperature Tempering of Martensitic Carbon Steel,” ChemRN: Metals & Alloys (Topic). 2019. link Times cited: 8 Abstract: Upon tempering of martensitic carbon steels, transition carb… read more USED (low confidence) H. Luu and N. Gunkelmann, “Pressure-induced phase transformations in Fe-C: Molecular dynamics approach,” Computational Materials Science. 2019. link Times cited: 24 USED (low confidence) T. Shimokawa, T. Niiyama, M. Okabe, and J. Sawakoshi, “Interfacial-dislocation-controlled deformation and fracture in nanolayered composites: Toward higher ductility of drawn pearlite,” Acta Materialia. 2019. link Times cited: 33 USED (low confidence) L. Qiao, T. Han, H. T. Wang, L. Han, and S. Gu, “Microscopic Study on Mechanical Properties of Different Microregions during In-Service Welding,” Materials Science Forum. 2019. link Times cited: 1 Abstract: In-service welding has been gaining considerable attentions … read more USED (low confidence) K. Saitoh, K. Oda, K. Yoshida, M. Takuma, Y. Takahashi, and T. Sato, “Atomistic Simulation of Heavily Plastic Deformation of Pearlitic Steel: Nano-sized Processes of Wiredrawing and Indentation,” IOP Conference Series: Materials Science and Engineering. 2018. link Times cited: 1 Abstract: We conduct molecular dynamics (MD) simulations of pearlitic … read more USED (low confidence) G. Bonny, N. Castin, A. Bakaev, and D. Terentyev, “Kinetic Monte Carlo model for 1-D migration in a field of strong traps: Application to self-interstitial clusters in W-Re alloys,” Computational Materials Science. 2018. link Times cited: 13 USED (low confidence) X. Chen, S. Lu, Z. Yang, T. Fu, C. Huang, and X. Peng, “Molecular dynamic simulation on nano-indentation of NiTi SMA,” Materials Science and Engineering A-structural Materials Properties Microstructure and Processing. 2018. link Times cited: 41 USED (low confidence) P. Ghosh, K. Ali, A. Vineet, A. Voleti, and A. Arya, “Study of structural, mechanical and thermal properties of θ-Fe3C, o-Fe7C3 and h-Fe7C3 phases using molecular dynamics simulations,” Journal of Alloys and Compounds. 2017. link Times cited: 12 USED (low confidence) M. A. Bhatia, S. Groh, and K. Solanki, “Atomic-scale investigation of point defects and hydrogen-solute atmospheres on the edge dislocation mobility in alpha iron,” Journal of Applied Physics. 2014. link Times cited: 36 Abstract: In this study, we present atomistic mechanisms of 1/2 [111](… read more USED (low confidence) F. Granberg, D. Terentyev, K. Henriksson, F. Djurabekova, and K. Nordlund, “Interaction of Dislocations with Carbides in BCC Fe Studied by Molecular Dynamics,” Fusion Science and Technology. 2014. link Times cited: 21 Abstract: Iron carbide (Fe3C), also known as cementite, is present in … read more USED (low confidence) B. Wang, E. Sak-Saracino, N. Gunkelmann, and H. Urbassek, “Molecular-dynamics study of the α ↔ γ phase transition in Fe–C,” Computational Materials Science. 2014. link Times cited: 37 USED (low confidence) H. Y. Li, X. Li, J. H. Li, J. Ma, and Y. Zhang, “Molecular Dynamics Simulation of TRIP Steel Residual Austenite Stacking Fault Development,” Advanced Materials Research. 2013. link Times cited: 0 Abstract: TRIP (Transformation induced plasticity) steel has a good co… read more USED (low confidence) N. Gunkelmann, E. Bringa, K. Kang, G. Ackland, C. Ruestes, and H. Urbassek, “Polycrystalline iron under compression: Plasticity and phase transitions,” Physical Review B. 2012. link Times cited: 85 USED (low confidence) Y. Abe, T. Suzudo, S. Jitsukawa, T. Tsuru, and T. Tsukada, “Effects of Carbon Impurity on Microstructural Evolution in Irradiated α-Iron,” Fusion Science and Technology. 2012. link Times cited: 12 Abstract: It is known that the presence of even a small amount of impu… read more USED (low confidence) J. Wallenius, N. Sandberg, and K. Henriksson, “Atomistic modelling of the Fe–Cr–C system,” Journal of Nuclear Materials. 2011. link Times cited: 3 USED (low confidence) R. M. Gerasimov, P. Volegov, and D. Gribov, “Modeling of microcracks and edge dislocations trapping of impurity atoms in Fe-C: MD simulation,” 29TH RUSSIAN CONFERENCE ON MATHEMATICAL MODELLING IN NATURAL SCIENCES. 2021. link Times cited: 0 USED (low confidence) R. M. Gerasimov and P. Volegov, “Modeling of microvoids as a mechanism of microdamages: MD simulations.” 2018. link Times cited: 1 USED (low confidence) R. Khanna and V. Sahajwalla, “Atomistic Simulations of Properties and Phenomena at High Temperatures.” 2014. link Times cited: 3 USED (low confidence) Y. Abe, T. Tsuru, and S. Jitsukawa, “Effect of Carbon Impurity Content on Microstructural Evolution in Neutron-Irradiated Alpha Iron: Cluster Dynamics Modeling,” MRS Proceedings. 2013. link Times cited: 0 USED (low confidence) D. Terentyev, N. Anento, and A. Serra, “Interaction of 〈1 0 0〉 loops with Carbon atoms and 〈1 0 0〉 dislocations in BCC Fe: An atomistic study,” Journal of Nuclear Materials. 2012. link Times cited: 15 USED (low confidence) E. Hristova, R. Janisch, R. Drautz, and A. Hartmaier, “Solubility of carbon in α-iron under volumetric strain and close to the Σ5(3 1 0)[0 0 1] grain boundary: Comparison of DFT and empirical potential methods,” Computational Materials Science. 2011. link Times cited: 46 NOT USED (low confidence) X. Fan, S. Gao, J. Zhang, and K. Jiao, “Analysis of the structure and viscosity of iron melts containing titanium at various concentration,” Journal of Molecular Liquids. 2023. link Times cited: 1 NOT USED (low confidence) S. S. M. N. Souq, F. A. Ghasemi, and M. M. S. Fakhrabadi, “Performance of different traditional and machine learning-based atomistic potential functions in the simulation of mechanical behavior of Fe nanowires,” Computational Materials Science. 2022. link Times cited: 0 NOT USED (low confidence) Y. Lei et al., “An Embedded-Atom Method Potential for studying the properties of Fe-Pb solid-liquid interface,” Journal of Nuclear Materials. 2022. link Times cited: 1 NOT USED (low confidence) S. Gao, K. Jiao, J. Zhang, X. Fan, and Y. Zong, “Association of atomic clusters and free volume with the viscosity of Fe-C melts,” Chemical Physics Letters. 2022. link Times cited: 1 NOT USED (low confidence) S. S. Sarangi and A. Kanjarla, “An atomistic study of the influence of carbon on the core structure of screw dislocation in BCC Fe and its consequences on non-Schmid behavior,” Materials Today Communications. 2022. link Times cited: 4 NOT USED (low confidence) U. Tewary et al., “The Origin of Graphite Morphology in Cast Iron,” Acta Materialia. 2022. link Times cited: 13 NOT USED (low confidence) K. Hyodo, S. Munetoh, and T. Tsuchiyama, “Empirical interatomic potential for Fe-C system using original Finnis-Sinclair potential function,” Computational Materials Science. 2020. link Times cited: 3 NOT USED (low confidence) L. S. I. Liyanage et al., “From Electrons to Atoms: Designing an Interatomic Potential for Fe-C Alloys.” 2018. link Times cited: 0 NOT USED (low confidence) M. Melnykov and R. Davidchack, “Characterization of melting properties of several Fe-C model potentials,” Computational Materials Science. 2018. link Times cited: 8 NOT USED (low confidence) M. Guziewski, S. Coleman, and C. Weinberger, “Atomistic investigation into the atomic structure and energetics of the ferrite-cementite interface: The Bagaryatskii orientation,” Acta Materialia. 2016. link Times cited: 34 NOT USED (low confidence) C. Barouh, T. Schuler, C. Fu, and M. Nastar, “Interaction between vacancies and interstitial solutes (C, N, and O) inα−Fe: From electronic structure to thermodynamics,” Physical Review B. 2014. link Times cited: 75 NOT USED (low confidence) R. Veiga, C. Becquart, and M. Perez, “Comments on ‘Atomistic modeling of an Fe system with a small concentration of C,’” Computational Materials Science. 2014. link Times cited: 35 NOT USED (low confidence) N. Anento and A. Serra, “Carbon–vacancy complexes as traps for self-interstitial clusters in Fe–C alloys,” Journal of Nuclear Materials. 2013. link Times cited: 38 NOT USED (low confidence) N. Gunkelmann, H. Ledbetter, and H. Urbassek, “Experimental and atomistic study of the elastic properties of α′ Fe–C martensite,” Acta Materialia. 2012. link Times cited: 38 NOT USED (low confidence) G. Ackland, “Temperature dependence in interatomic potentials and an improved potential for Ti,” Journal of Physics: Conference Series. 2012. link Times cited: 11 Abstract: The process of deriving an interatomic potentials represents… read more NOT USED (low confidence) D. Terentyev, N. Anento, A. Serra, V. Jansson, H. Khater, and G. Bonny, “Interaction of carbon with vacancy and self-interstitial atom clusters in α-iron studied using metallic-covalent interatomic potential,” Journal of Nuclear Materials. 2011. link Times cited: 57 NOT USED (low confidence) L. Malerba et al., “Comparison of empirical interatomic potentials for iron applied to radiation damage studies,” Journal of Nuclear Materials. 2010. link Times cited: 210 NOT USED (low confidence) N. Gao, M. Samaras, and H. Swygenhoven, “A new Fe–He pair potential,” Journal of Nuclear Materials. 2010. link Times cited: 22 NOT USED (low confidence) J. Crocombette and F. Willaime, “Ab Initio Electronic Structure Calculations for Nuclear Materials,” Comprehensive Nuclear Materials. 2020. link Times cited: 11 NOT USED (low confidence) G. Ackland and G. Bonny, “Interatomic Potential Development,” Comprehensive Nuclear Materials. 2020. link Times cited: 4 NOT USED (low confidence) G. Ackland, “1.10 – Interatomic Potential Development.” 2012. link Times cited: 10 NOT USED (high confidence) A. Front et al., “Simulation of thermodynamic properties of magnetic transition metals from an efficient tight-binding model: The case of cobalt and beyond,” Physical Review B. 2021. link Times cited: 0 Abstract: Alexis Front, ∗ Georg Daniel Förster, 2, † Van-Truong Tran, … read more NOT USED (high confidence) Z. Cheng, H. Wang, and G.-rong Liu, “Fatigue crack propagation in carbon steel using RVE based model,” ArXiv. 2021. link Times cited: 11 NOT USED (high confidence) S. A. Fadhil, J. H. Azeez, and M. Hassan, “Derivation of a new multiscale model: I. Derivation of the model for the atomic, molecular and nano material scales,” Indian Journal of Physics. 2020. link Times cited: 5 NOT USED (high confidence) X. W. Zhou, M. E. Foster, J. Ronevich, and C. S. Marchi, “Review and construction of interatomic potentials for molecular dynamics studies of hydrogen embrittlement in Fe─C based steels,” Journal of Computational Chemistry. 2020. link Times cited: 7 Abstract: Reducing hydrogen embrittlement in the low‐cost Fe─C based s… read more NOT USED (high confidence) N. Hoc, L. Việt, and N. Dũng, “On the Melting of Defective FCC Interstitial Alloy γ-FeC under Pressure up to 100 GPa,” Journal of Electronic Materials. 2019. link Times cited: 15 NOT USED (high confidence) L. Wang, J. Jin, P. Yang, Y. Zong, and Q. Peng, “Graphene Adhesion Mechanics on Iron Substrates: Insight from Molecular Dynamic Simulations,” Crystals. 2019. link Times cited: 8 Abstract: The adhesion feature of graphene on metal substrates is impo… read more NOT USED (high confidence) T. Wen et al., “Development of a deep machine learning interatomic potential for metalloid-containing Pd-Si compounds,” Physical Review B. 2019. link Times cited: 30 Abstract: Interatomic potentials based on neural-network machine learn… read more NOT USED (high confidence) S. Teus and V. Gavriljuk, “Molecular Dynamics Study of the Hydrogen and Carbon Effect on Mobility of Grain Boundaries in α-Iron,” METALLOFIZIKA I NOVEISHIE TEKHNOLOGII. 2019. link Times cited: 0 NOT USED (high confidence) H. Luu, R. Veiga, and N. Gunkelmann, “Atomistic Study of the Role of Defects on α → ϵ Phase Transformations in Iron under Hydrostatic Compression,” Metals. 2019. link Times cited: 13 Abstract: It has long been known that iron undergoes a phase transform… read more NOT USED (high confidence) I. A. Alhafez and H. Urbassek, “Influence of tip adhesion on nanoindentation and scratching,” Modelling and Simulation in Materials Science and Engineering. 2019. link Times cited: 9 Abstract: Using molecular dynamics simulation, we study the influence … read more NOT USED (high confidence) G. Bonny, A. Bakaev, and D. Terentyev, “Energetic Stability of Vacancy‐Carbon Clusters in Solid Solution Alloys: The Fe‐Cr‐C Case,” physica status solidi (b). 2019. link Times cited: 4 Abstract: In carbon‐containing alloys, the energetic stability of vaca… read more NOT USED (high confidence) J. Wang et al., “Greater diffusion rate of carbon atoms from nonlinear migration in micro-cell and spatially heterogeneous stable states in FCC iron,” Journal of Materials Science. 2018. link Times cited: 2 NOT USED (high confidence) R. Candela, N. Mousseau, R. G. A. Veiga, C. Domain, C. Becquart, and C. Becquart, “Interaction between interstitial carbon atoms and a ½ 〈1 1 1〉 self-interstitial atoms loop in an iron matrix: a combined DFT, off lattice KMC and MD study,” Journal of Physics: Condensed Matter. 2018. link Times cited: 4 Abstract: A static and kinetic study of the interaction between a 19 ½… read more NOT USED (high confidence) Y.-T. Zheng, M. He, G. Cheng, Z.-xiao Zhang, F. Xuan, and Z. Wang, “Molecular dynamics simulation of tensile strain-altered hydrogen behaviour and its effects on local plasticity,” Molecular Simulation. 2018. link Times cited: 2 Abstract: Using molecular dynamics simulation, local plasticity of bcc… read more NOT USED (high confidence) D. Dragoni, T. Daff, G. Csányi, and N. Marzari, “Achieving DFT accuracy with a machine-learning interatomic potential: thermomechanics and defects in bcc ferromagnetic iron,” arXiv: Materials Science. 2017. link Times cited: 167 Abstract: We show that the Gaussian Approximation Potential machine le… read more NOT USED (high confidence) K. Matous, M. Geers, V. Kouznetsova, and A. Gillman, “A review of predictive nonlinear theories for multiscale modeling of heterogeneous materials,” J. Comput. Phys. 2017. link Times cited: 365 NOT USED (high confidence) J. Janssen, N. Gunkelmann, and H. Urbassek, “Influence of C concentration on elastic moduli of α′-Fe1-xCx alloys,” Philosophical Magazine. 2016. link Times cited: 9 Abstract: The elastic constants of tetragonally distorted - crystallit… read more NOT USED (high confidence) C. P. Chui, W. Liu, Y. Xu, and Y. Zhou, “Molecular Dynamics Simulation of Iron — A Review.” 2015. link Times cited: 3 Abstract: Molecular dynamics (MD) is a technique of atomistic simulati… read more NOT USED (high confidence) M. E. Ford, D. Pettifor, and R. Drautz, “Non-collinear magnetism with analytic Bond-Order Potentials,” Journal of Physics: Condensed Matter. 2015. link Times cited: 8 Abstract: The theory of analytic Bond-Order Potentials as applied to n… read more NOT USED (high confidence) T. Kumagai, K. Nakamura, S. Yamada, and T. Ohnuma, “Simple bond-order-type interatomic potential for an intermixed Fe-Cr-C system of metallic and covalent bondings in heat-resistant ferritic steels,” Journal of Applied Physics. 2014. link Times cited: 1 Abstract: It is known that M23C6(M = Cr/Fe) behavior in heat-resistant… read more NOT USED (high confidence) B. Wang, E. Sak-Saracino, L. Sandoval, and H. Urbassek, “Martensitic and austenitic phase transformations in Fe–C nanowires,” Modelling and Simulation in Materials Science and Engineering. 2014. link Times cited: 17 Abstract: Using molecular-dynamics simulation, we study the austenitic… read more NOT USED (high confidence) N. Hatcher, G. Madsen, and R. Drautz, “Parameterized electronic description of carbon cohesion in iron grain boundaries,” Journal of Physics: Condensed Matter. 2014. link Times cited: 7 Abstract: We employ a recently developed iron–carbon orthogonal tight-… read more NOT USED (high confidence) M. E. Ford, R. Drautz, T. Hammerschmidt, and D. Pettifor, “Convergence of an analytic bond-order potential for collinear magnetism in Fe,” Modelling and Simulation in Materials Science and Engineering. 2014. link Times cited: 20 Abstract: Analytic bond-order potentials (BOPs) for magnetic transitio… read more NOT USED (high confidence) T. Shimokawa, T. Oguro, M. Tanaka, K. Higashida, and T. Ohashi, “A multiscale approach for the deformation mechanism in pearlite microstructure: Atomistic study of the role of the heterointerface on ductility,” Materials Science and Engineering A-structural Materials Properties Microstructure and Processing. 2014. link Times cited: 24 NOT USED (high confidence) E. Sak-Saracino and H. Urbassek, “Free energies of austenite and martensite Fe–C alloys: an atomistic study,” Philosophical Magazine. 2014. link Times cited: 12 Abstract: We investigate the influence of C interstitials on the phase… read more NOT USED (high confidence) K. Henriksson, C. Björkas, and K. Nordlund, “Atomistic simulations of stainless steels: a many-body potential for the Fe–Cr–C system,” Journal of Physics: Condensed Matter. 2013. link Times cited: 65 Abstract: Stainless steels found in real-world applications usually ha… read more NOT USED (high confidence) D. Terentyev, N. Anento, and A. Serra, “Interaction of dislocations with carbon-decorated dislocation loops in bcc Fe: an atomistic study,” Journal of Physics: Condensed Matter. 2012. link Times cited: 16 Abstract: Properties of ferritic Fe-based alloys are highly sensitive … read more NOT USED (high confidence) Y. You and M. Yan, “Many-body potential for nitrogen in α-iron,” Philosophical Magazine Letters. 2012. link Times cited: 3 Abstract: N atom is one of the most frequent foreign interstitial atom… read more NOT USED (high confidence) D. Terentyev, G. Bonny, A. Bakaev, and D. V. Neck, “On the thermal stability of vacancy–carbon complexes in alpha iron,” Journal of Physics: Condensed Matter. 2012. link Times cited: 20 Abstract: In this work we have summarized the available ab initio data… read more NOT USED (high confidence) G. Ackland, T. P. C. Klaver, and D. Hepburn, “First Principles Calculations of Defects in Unstable Crystals: Austenitic Iron,” arXiv: Materials Science. 2011. link Times cited: 0 Abstract: First principles calculations have given a new insight into … read more NOT USED (high confidence) L. Malerba et al., “Ab initio calculations and interatomic potentials for iron and iron alloys : Achievements within the Perfect Project,” Journal of Nuclear Materials. 2010. link Times cited: 65 NOT USED (high confidence) C. Borchers, Y. Chen, M. Deutges, S. Goto, and R. Kirchheim, “Carbon-defect interaction during recovery and recrystallization of heavily deformed pearlitic steel wires,” Philosophical Magazine Letters. 2010. link Times cited: 21 Abstract: Cold-drawn pearlitic steel wires are known to exhibit increa… read more NOT USED (high confidence) G. Bonny and R. Pasianot, “Gauge transformations to combine multi-component many-body interatomic potentials,” Philosophical Magazine Letters. 2010. link Times cited: 19 Abstract: Many-body interatomic potentials play an important role in a… read more NOT USED (high confidence) A. Duff and M. Sluiter, “Diagnostic Structures for Interatomic Potentials,” Materials Transactions. 2010. link Times cited: 3 Abstract: unrelaxed structures are easily reproducible, enabling them … read more NOT USED (high confidence) L. Lymperakis, M. Friák, and J. Neugebauer, “Atomistic calculations on interfaces: Bridging the length and time scales,” The European Physical Journal Special Topics. 2009. link Times cited: 8 NOT USED (high confidence) K. Henriksson and K. Nordlund, “Simulations of cementite: An analytical potential for the Fe-C system,” Physical Review B. 2009. link Times cited: 72 Abstract: An analytical bond-order interatomic potential has been deve… read more NOT USED (definite) J. Meiser and H. Urbassek, “Effect of Alloying Elements on the α-γ Phase Transformation in Iron,” Materials. 2019. link Times cited: 2 Abstract: Small concentrations of alloying elements can modify the α-γ… read more NOT USED (definite) S. Karewar, J. Sietsma, and M. Santofimia, “Effect of C on the Martensitic Transformation in Fe-C Alloys in the Presence of Pre-Existing Defects: A Molecular Dynamics Study,” Crystals. 2019. link Times cited: 19 Abstract: Molecular dynamics simulations are used to investigate the a… read more NOT USED (definite) G. J. Ackland, K. D’Mellow, S. L. Daraszewicz, D. J. Hepburn, M. Uhrin, and K.Stratford, “The MOLDY short-range molecular dynamics package,” Comput. Phys. Commun. 2011. link Times cited: 37 |
| Funding | Not available |
| Short KIM ID
The unique KIM identifier code.
| MO_143977152728_005 |
| Extended KIM ID
The long form of the KIM ID including a human readable prefix (100 characters max), two underscores, and the Short KIM ID. Extended KIM IDs can only contain alpha-numeric characters (letters and digits) and underscores and must begin with a letter.
| EAM_Dynamo_HepburnAckland_2008_FeC__MO_143977152728_005 |
| DOI |
10.25950/a38f2843 https://doi.org/10.25950/a38f2843 https://commons.datacite.org/doi.org/10.25950/a38f2843 |
| KIM Item Type
Specifies whether this is a Portable Model (software implementation of an interatomic model); Portable Model with parameter file (parameter file to be read in by a Model Driver); Model Driver (software implementation of an interatomic model that reads in parameters).
| Portable Model using Model Driver EAM_Dynamo__MD_120291908751_005 |
| Driver | EAM_Dynamo__MD_120291908751_005 |
| KIM API Version | 2.0 |
| Potential Type | eam |
| Programming Language(s)
The programming languages used in the code and the percentage of the code written in each one. "N/A" means "not applicable" and refers to model parameterizations which only include parameter tables and have no programming language.
| N/A |
| Previous Version | EAM_Dynamo_HepburnAckland_2008_FeC__MO_143977152728_004 |
| Grade | Name | Category | Brief Description | Full Results | Aux File(s) |
|---|---|---|---|---|---|
| P | vc-species-supported-as-stated | mandatory | The model supports all species it claims to support; see full description. |
Results | Files |
| P | vc-periodicity-support | mandatory | Periodic boundary conditions are handled correctly; see full description. |
Results | Files |
| P | vc-permutation-symmetry | mandatory | Total energy and forces are unchanged when swapping atoms of the same species; see full description. |
Results | Files |
| B | vc-forces-numerical-derivative | consistency | Forces computed by the model agree with numerical derivatives of the energy; see full description. |
Results | Files |
| F | vc-dimer-continuity-c1 | informational | The energy versus separation relation of a pair of atoms is C1 continuous (i.e. the function and its first derivative are continuous); see full description. |
Results | Files |
| P | vc-objectivity | informational | Total energy is unchanged and forces transform correctly under rigid-body translation and rotation; see full description. |
Results | Files |
| P | vc-inversion-symmetry | informational | Total energy is unchanged and forces change sign when inverting a configuration through the origin; see full description. |
Results | Files |
| N/A | vc-memory-leak | informational | The model code does not have memory leaks (i.e. it releases all allocated memory at the end); see full description. |
Results | Files |
| P | vc-thread-safe | mandatory | The model returns the same energy and forces when computed in serial and when using parallel threads for a set of configurations. Note that this is not a guarantee of thread safety; see full description. |
Results | Files |
| P | vc-unit-conversion | mandatory | The model is able to correctly convert its energy and/or forces to different unit sets; see full description. |
Results | Files |
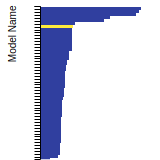
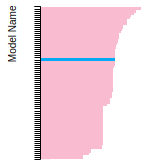
BCC Lattice Constant
This bar chart plot shows the mono-atomic body-centered cubic (bcc) lattice constant predicted by the current model (shown in the unique color) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
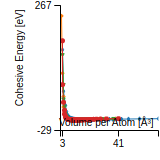
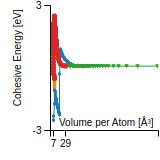
Cohesive Energy Graph
This graph shows the cohesive energy versus volume-per-atom for the current mode for four mono-atomic cubic phases (body-centered cubic (bcc), face-centered cubic (fcc), simple cubic (sc), and diamond). The curve with the lowest minimum is the ground state of the crystal if stable. (The crystal structure is enforced in these calculations, so the phase may not be stable.) Graphs are generated for each species supported by the model.
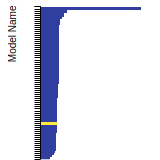
Diamond Lattice Constant
This bar chart plot shows the mono-atomic face-centered diamond lattice constant predicted by the current model (shown in the unique color) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
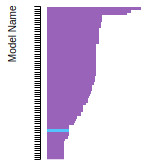
Dislocation Core Energies
This graph shows the dislocation core energy of a cubic crystal at zero temperature and pressure for a specific set of dislocation core cutoff radii. After obtaining the total energy of the system from conjugate gradient minimizations, non-singular, isotropic and anisotropic elasticity are applied to obtain the dislocation core energy for each of these supercells with different dipole distances. Graphs are generated for each species supported by the model.
(No matching species)FCC Elastic Constants
This bar chart plot shows the mono-atomic face-centered cubic (fcc) elastic constants predicted by the current model (shown in blue) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
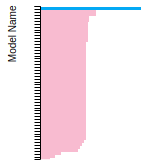
FCC Lattice Constant
This bar chart plot shows the mono-atomic face-centered cubic (fcc) lattice constant predicted by the current model (shown in red) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
FCC Stacking Fault Energies
This bar chart plot shows the intrinsic and extrinsic stacking fault energies as well as the unstable stacking and unstable twinning energies for face-centered cubic (fcc) predicted by the current model (shown in blue) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
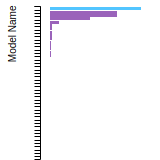
(No matching species)FCC Surface Energies
This bar chart plot shows the mono-atomic face-centered cubic (fcc) relaxed surface energies predicted by the current model (shown in blue) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
(No matching species)SC Lattice Constant
This bar chart plot shows the mono-atomic simple cubic (sc) lattice constant predicted by the current model (shown in the unique color) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
Cubic Crystal Basic Properties Table
Species: CSpecies: Fe
Disclaimer From Model Developer
Does not describe cementite. Does not describe Carbon.
Creators: Daniel S. Karls
Contributor: karls
Publication Year: 2018
DOI: https://doi.org/10.25950/c6746c52
This Test Driver uses LAMMPS to compute the cohesive energy of a given monoatomic cubic lattice (fcc, bcc, sc, or diamond) at a variety of lattice spacings. The lattice spacings range from a_min (=a_min_frac*a_0) to a_max (=a_max_frac*a_0) where a_0, a_min_frac, and a_max_frac are read from stdin (a_0 is typically approximately equal to the equilibrium lattice constant). The precise scaling and number of lattice spacings sampled between a_min and a_0 (a_0 and a_max) is specified by two additional parameters passed from stdin: N_lower and samplespacing_lower (N_upper and samplespacing_upper). Please see README.txt for further details.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Cohesive energy versus lattice constant curve for sc Carbon | view | 14515 |
Creators:
Contributor: karls
Publication Year: 2019
DOI: https://doi.org/10.25950/64cb38c5
This Test Driver uses LAMMPS to compute the cohesive energy of a given monoatomic cubic lattice (fcc, bcc, sc, or diamond) at a variety of lattice spacings. The lattice spacings range from a_min (=a_min_frac*a_0) to a_max (=a_max_frac*a_0) where a_0, a_min_frac, and a_max_frac are read from stdin (a_0 is typically approximately equal to the equilibrium lattice constant). The precise scaling and number of lattice spacings sampled between a_min and a_0 (a_0 and a_max) is specified by two additional parameters passed from stdin: N_lower and samplespacing_lower (N_upper and samplespacing_upper). Please see README.txt for further details.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Cohesive energy versus lattice constant curve for bcc C v004 | view | 47895 | |
| Cohesive energy versus lattice constant curve for bcc Fe v004 | view | 73314 | |
| Cohesive energy versus lattice constant curve for diamond C v004 | view | 49547 | |
| Cohesive energy versus lattice constant curve for diamond Fe v004 | view | 58592 | |
| Cohesive energy versus lattice constant curve for fcc C v004 | view | 44099 | |
| Cohesive energy versus lattice constant curve for fcc Fe v004 | view | 62058 | |
| Cohesive energy versus lattice constant curve for sc Fe v004 | view | 63251 |
Creators:
Contributor: ilia
Publication Year: 2024
DOI: https://doi.org/10.25950/888f9943
Computes the elastic constants for an arbitrary crystal. A robust computational protocol is used, attempting multiple methods and step sizes to achieve an acceptably low error in numerical differentiation and deviation from material symmetry. The crystal structure is specified using the AFLOW prototype designation as part of the Crystal Genome testing framework. In addition, the distance from the obtained elasticity tensor to the nearest isotropic tensor is computed.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Elastic constants for CFe in AFLOW crystal prototype A2B5_mC28_15_f_e2f at zero temperature and pressure v000 | view | 1841393 |
Creators: Junhao Li
Contributor: jl2922
Publication Year: 2018
DOI: https://doi.org/10.25950/75393d88
Computes the cubic elastic constants for some common crystal types (fcc, bcc, sc) by calculating the hessian of the energy density with respect to strain. An estimate of the error associated with the numerical differentiation performed is reported.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Elastic constants for sc C at zero temperature | view | 3079 |
Creators: Junhao Li and Ellad Tadmor
Contributor: tadmor
Publication Year: 2019
DOI: https://doi.org/10.25950/5853fb8f
Computes the cubic elastic constants for some common crystal types (fcc, bcc, sc, diamond) by calculating the hessian of the energy density with respect to strain. An estimate of the error associated with the numerical differentiation performed is reported.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Elastic constants for bcc C at zero temperature v006 | view | 1727 | |
| Elastic constants for bcc Fe at zero temperature v006 | view | 2047 | |
| Elastic constants for fcc C at zero temperature v006 | view | 1567 | |
| Elastic constants for fcc Fe at zero temperature v006 | view | 1759 | |
| Elastic constants for sc Fe at zero temperature v006 | view | 2079 |
Creators: Junhao Li
Contributor: jl2922
Publication Year: 2018
DOI: https://doi.org/10.25950/2e4b93d9
Computes the elastic constants for hcp crystals by calculating the hessian of the energy density with respect to strain. An estimate of the error associated with the numerical differentiation performed is reported.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Elastic constants for hcp C at zero temperature | view | 3959 |
Creators: Junhao Li
Contributor: jl2922
Publication Year: 2019
DOI: https://doi.org/10.25950/d794c746
Computes the elastic constants for hcp crystals by calculating the hessian of the energy density with respect to strain. An estimate of the error associated with the numerical differentiation performed is reported.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Elastic constants for hcp Fe at zero temperature v004 | view | 1846 |
Creators:
Contributor: ilia
Publication Year: 2024
DOI: https://doi.org/10.25950/2f2c4ad3
Computes the equilibrium crystal structure and energy for an arbitrary crystal at zero temperature and applied stress by performing symmetry-constrained relaxation. The crystal structure is specified using the AFLOW prototype designation. Multiple sets of free parameters corresponding to the crystal prototype may be specified as initial guesses for structure optimization. No guarantee is made regarding the stability of computed equilibria, nor that any are the ground state.
Creators:
Contributor: ilia
Publication Year: 2025
DOI: https://doi.org/10.25950/866c7cfa
Computes the equilibrium crystal structure and energy for an arbitrary crystal at zero temperature and applied stress by performing symmetry-constrained relaxation. The crystal structure is specified using the AFLOW prototype designation. Multiple sets of free parameters corresponding to the crystal prototype may be specified as initial guesses for structure optimization. No guarantee is made regarding the stability of computed equilibria, nor that any are the ground state.
Creators: Brandon Runnels
Contributor: brunnels
Publication Year: 2019
DOI: https://doi.org/10.25950/4723cee7
Computes grain boundary energy for a range of tilt angles given a crystal structure, tilt axis, and material.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Relaxed energy as a function of tilt angle for a 112 symmetric tilt grain boundary in fcc Fe v000 | view | 112385754 |
Creators:
Contributor: brunnels
Publication Year: 2022
DOI: https://doi.org/10.25950/2c59c9d6
Computes grain boundary energy for a range of tilt angles given a crystal structure, tilt axis, and material.
Creators: Junhao Li
Contributor: jl2922
Publication Year: 2018
DOI: https://doi.org/10.25950/f3eec5a9
Equilibrium lattice constant and cohesive energy of a cubic lattice at zero temperature and pressure.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Equilibrium zero-temperature lattice constant for sc C | view | 1649 |
Creators: Daniel S. Karls and Junhao Li
Contributor: karls
Publication Year: 2019
DOI: https://doi.org/10.25950/2765e3bf
Equilibrium lattice constant and cohesive energy of a cubic lattice at zero temperature and pressure.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Equilibrium zero-temperature lattice constant for bcc C v007 | view | 3231 | |
| Equilibrium zero-temperature lattice constant for bcc Fe v007 | view | 3103 | |
| Equilibrium zero-temperature lattice constant for diamond C v007 | view | 3775 | |
| Equilibrium zero-temperature lattice constant for diamond Fe v007 | view | 5630 | |
| Equilibrium zero-temperature lattice constant for fcc C v007 | view | 5758 | |
| Equilibrium zero-temperature lattice constant for fcc Fe v007 | view | 6110 | |
| Equilibrium zero-temperature lattice constant for sc Fe v007 | view | 3647 |
Creators: Junhao Li
Contributor: jl2922
Publication Year: 2018
DOI: https://doi.org/10.25950/25bcc28b
Calculates lattice constant of hexagonal bulk structures at zero temperature and pressure by using simplex minimization to minimize the potential energy.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Equilibrium lattice constants for hcp C | view | 14515 |
Creators: Daniel S. Karls and Junhao Li
Contributor: karls
Publication Year: 2019
DOI: https://doi.org/10.25950/c339ca32
Calculates lattice constant of hexagonal bulk structures at zero temperature and pressure by using simplex minimization to minimize the potential energy.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Equilibrium lattice constants for hcp Fe v005 | view | 31008 |
Creators:
Contributor: mjwen
Publication Year: 2024
DOI: https://doi.org/10.25950/9d9822ec
This Test Driver uses LAMMPS to compute the linear thermal expansion coefficient at a finite temperature under a given pressure for a cubic lattice (fcc, bcc, sc, diamond) of a single given species.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Linear thermal expansion coefficient of bcc Fe at 293.15 K under a pressure of 0 MPa v002 | view | 363709 |
Creators: Matt Bierbaum
Contributor: mattbierbaum
Publication Year: 2019
DOI: https://doi.org/10.25950/6c43a4e6
Calculates the surface energy of several high symmetry surfaces and produces a broken-bond model fit. In latex form, the fit equations are given by:
E_{FCC} (\vec{n}) = p_1 (4 \left( |x+y| + |x-y| + |x+z| + |x-z| + |z+y| +|z-y|\right)) + p_2 (8 \left( |x| + |y| + |z|\right)) + p_3 (2 ( |x+ 2y + z| + |x+2y-z| + |x-2y + z| + |x-2y-z| + |2x+y+z| + |2x+y-z| +|2x-y+z| +|2x-y-z| +|x+y+2z| +|x+y-2z| +|x-y+2z| +|x-y-2z| ) + c
E_{BCC} (\vec{n}) = p_1 (6 \left( | x+y+z| + |x+y-z| + |-x+y-z| + |x-y+z| \right)) + p_2 (8 \left( |x| + |y| + |z|\right)) + p_3 (4 \left( |x+y| + |x-y| + |x+z| + |x-z| + |z+y| +|z-y|\right)) +c.
In Python, these two fits take the following form:
def BrokenBondFCC(params, index):
import numpy
x, y, z = index
x = x / numpy.sqrt(x**2.+y**2.+z**2.)
y = y / numpy.sqrt(x**2.+y**2.+z**2.)
z = z / numpy.sqrt(x**2.+y**2.+z**2.)
return params[0]*4* (abs(x+y) + abs(x-y) + abs(x+z) + abs(x-z) + abs(z+y) + abs(z-y)) + params[1]*8*(abs(x) + abs(y) + abs(z)) + params[2]*(abs(x+2*y+z) + abs(x+2*y-z) +abs(x-2*y+z) +abs(x-2*y-z) + abs(2*x+y+z) +abs(2*x+y-z) +abs(2*x-y+z) +abs(2*x-y-z) + abs(x+y+2*z) +abs(x+y-2*z) +abs(x-y+2*z) +abs(x-y-2*z))+params[3]
def BrokenBondBCC(params, x, y, z):
import numpy
x, y, z = index
x = x / numpy.sqrt(x**2.+y**2.+z**2.)
y = y / numpy.sqrt(x**2.+y**2.+z**2.)
z = z / numpy.sqrt(x**2.+y**2.+z**2.)
return params[0]*6*(abs(x+y+z) + abs(x-y-z) + abs(x-y+z) + abs(x+y-z)) + params[1]*8*(abs(x) + abs(y) + abs(z)) + params[2]*4* (abs(x+y) + abs(x-y) + abs(x+z) + abs(x-z) + abs(z+y) + abs(z-y)) + params[3]
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Broken-bond fit of high-symmetry surface energies in bcc Fe v004 | view | 17722 |
Creators:
Contributor: efuem
Publication Year: 2023
DOI: https://doi.org/10.25950/fca89cea
Computes the monovacancy formation energy and relaxation volume for cubic and hcp monoatomic crystals.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Monovacancy formation energy and relaxation volume for bcc Fe | view | 367293 |
Creators:
Contributor: efuem
Publication Year: 2023
DOI: https://doi.org/10.25950/c27ba3cd
Computes the monovacancy formation and migration energies for cubic and hcp monoatomic crystals.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Vacancy formation and migration energy for bcc Fe | view | 3996562 |
| Test | Error Categories | Link to Error page |
|---|---|---|
| Elastic constants for diamond C at zero temperature v001 | other | view |
| Elastic constants for diamond Fe at zero temperature v001 | other | view |
EquilibriumCrystalStructure__TD_457028483760_000
| Test | Error Categories | Link to Error page |
|---|---|---|
| Equilibrium crystal structure and energy for Fe in AFLOW crystal prototype A_tP28_136_f2ij v000 | other | view |
EquilibriumCrystalStructure__TD_457028483760_003
| Test | Error Categories | Link to Error page |
|---|---|---|
| Equilibrium crystal structure and energy for CFe in AFLOW crystal prototype A2B5_aP28_2_4i_10i v003 | other | view |
| Equilibrium crystal structure and energy for Fe in AFLOW crystal prototype A_tP1_123_a v003 | other | view |
GrainBoundaryCubicCrystalSymmetricTiltRelaxedEnergyVsAngle__TD_410381120771_003
| Test | Error Categories | Link to Error page |
|---|---|---|
| Relaxed energy as a function of tilt angle for a 112 symmetric tilt grain boundary in fcc Fe v001 | other | view |
LatticeConstant2DHexagonalEnergy__TD_034540307932_002
| Test | Error Categories | Link to Error page |
|---|---|---|
| Cohesive energy and equilibrium lattice constant of graphene v002 | other | view |
LatticeConstantCubicEnergy__TD_475411767977_006
| Test | Error Categories | Link to Error page |
|---|---|---|
| Equilibrium zero-temperature lattice constant for diamond C | other | view |
| Equilibrium zero-temperature lattice constant for diamond Fe | other | view |
LatticeConstantCubicEnergy__TD_475411767977_007
| Test | Error Categories | Link to Error page |
|---|---|---|
| Equilibrium zero-temperature lattice constant for sc C v007 | other | view |
LatticeConstantHexagonalEnergy__TD_942334626465_005
| Test | Error Categories | Link to Error page |
|---|---|---|
| Equilibrium lattice constants for hcp C v005 | other | view |
LinearThermalExpansionCoeffCubic__TD_522633393614_002
| Test | Error Categories | Link to Error page |
|---|---|---|
| Linear thermal expansion coefficient of diamond C at 293.15 K under a pressure of 0 MPa v002 | other | view |
| EAM_Dynamo_HepburnAckland_2008_FeC__MO_143977152728_005.txz | Tar+XZ | Linux and OS X archive |
| EAM_Dynamo_HepburnAckland_2008_FeC__MO_143977152728_005.zip | Zip | Windows archive |
This Model requires a Model Driver. Archives for the Model Driver EAM_Dynamo__MD_120291908751_005 appear below.
| EAM_Dynamo__MD_120291908751_005.txz | Tar+XZ | Linux and OS X archive |
| EAM_Dynamo__MD_120291908751_005.zip | Zip | Windows archive |