EAM_Dynamo_MendelevSordeletKramer_2007_CuZr__MO_120596890176_005
EAM_Dynamo_MendelevSordeletKramer_2007_CuZr__MO_120596890176_005
| Title
A single sentence description.
|
Finnis-Sinclair potential (LAMMPS cubic hermite tabulation) for the Cu-Zr system developed by Mendelev, Sordelet and Kramer (2007) v005 |
|---|---|
| Description
A short description of the Model describing its key features including for example: type of model (pair potential, 3-body potential, EAM, etc.), modeled species (Ac, Ag, ..., Zr), intended purpose, origin, and so on.
|
We propose a method of using atomistic computer simulations to obtain partial pair correlation functions from wide angle diffraction experiments with metallic liquids and their glasses. In this method, a model is first created using a semiempirical interatomic potential and then an additional atomic force is added to improve the agreement with experimental diffraction data. To illustrate this approach, the structure of an amorphous Cu64.5Zr35.5 alloy is highlighted, where we present the results for the semiempirical many-body potential and fitting to x-ray diffraction data. While only x-ray diffraction data were used in the present work, the method can be easily adapted to the case when there are also data from neutron diffraction or even in combination. Moreover, this method can be employed in the case of multicomponent systems when the data of several diffraction experiments can be combined. Note that the version published in [M.I. Mendelev, M.J. Kramer, R.T. Ott, D.J. Sordelet, D. Yagodin and P. Popel, Phil. Mag. 89, 967-987 (2009).] is better for simulation of liquid/glass structure. |
| Species
The supported atomic species.
| Cu, Zr |
| Disclaimer
A statement of applicability provided by the contributor, informing users of the intended use of this KIM Item.
|
The authors note in the paper that this potential was never intended for serious simulation. An improved Cu-Zr model can be found in KIM item https://openkim.org/id/MO_609260676108_000. |
| Content Origin | http://www.ctcms.nist.gov/potentials/Cu.html |
| Contributor |
Mikhail I. Mendelev |
| Maintainer |
Mikhail I. Mendelev |
| Developer |
Dan J. Sordelet Matthew J. Kramer Mikhail I. Mendelev |
| Published on KIM | 2018 |
| How to Cite | Click here to download this citation in BibTeX format. |
| Citations
This panel presents information regarding the papers that have cited the interatomic potential (IP) whose page you are on. The OpenKIM machine learning based Deep Citation framework is used to determine whether the citing article actually used the IP in computations (denoted by "USED") or only provides it as a background citation (denoted by "NOT USED"). For more details on Deep Citation and how to work with this panel, click the documentation link at the top of the panel. The word cloud to the right is generated from the abstracts of IP principle source(s) (given below in "How to Cite") and the citing articles that were determined to have used the IP in order to provide users with a quick sense of the types of physical phenomena to which this IP is applied. The bar chart shows the number of articles that cited the IP per year. Each bar is divided into green (articles that USED the IP) and blue (articles that did NOT USE the IP). Users are encouraged to correct Deep Citation errors in determination by clicking the speech icon next to a citing article and providing updated information. This will be integrated into the next Deep Citation learning cycle, which occurs on a regular basis. OpenKIM acknowledges the support of the Allen Institute for AI through the Semantic Scholar project for providing citation information and full text of articles when available, which are used to train the Deep Citation ML algorithm. |
This panel provides information on past usage of this interatomic potential (IP) powered by the OpenKIM Deep Citation framework. The word cloud indicates typical applications of the potential. The bar chart shows citations per year of this IP (bars are divided into articles that used the IP (green) and those that did not (blue)). The complete list of articles that cited this IP is provided below along with the Deep Citation determination on usage. See the Deep Citation documentation for more information. 
282 Citations (243 used)
Help us to determine which of the papers that cite this potential actually used it to perform calculations. If you know, click the .
USED (definite) D. Şopu, X. Yuan, F. Moitzi, M. Stoica, and J. Eckert, “Structure–Property Relationships in Shape Memory Metallic Glass Composites,” Materials. 2019. link Times cited: 23 Abstract: Metallic glass composites with shape memory crystals show en… read more USED (definite) K. E. Avila, S. Küchemann, I. A. Alhafez, and H. Urbassek, “Shear-Transformation Zone Activation during Loading and Unloading in Nanoindentation of Metallic Glasses,” Materials. 2019. link Times cited: 26 Abstract: Using molecular dynamics simulation, we study nanoindentatio… read more USED (definite) P.-wei Wang, H. Li, and L. Yang, “Free Volume Contributing to the Different Yield Behaviors between Tension and Compression Deformations in Metallic Glasses.” 2017. link Times cited: 8 Abstract: The different deformation behaviors in the yield stage, in p… read more USED (definite) C. Zhong et al., “Non-localized deformation in CuZr multi-layer amorphous films under tension,” Journal of Alloys and Compounds. 2016. link Times cited: 36 USED (definite) X. Huang, Z. Ling, Y. Wang, and L. Dai, “Intrinsic structural defects on medium range in metallic glasses,” Intermetallics. 2016. link Times cited: 16 USED (definite) D. Şopu, C. Soyarslan, B. Sarac, S. Bargmann, M. Stoica, and J. Eckert, “Structure-property relationships in nanoporous metallic glasses,” Acta Materialia. 2016. link Times cited: 87 USED (definite) M. Sepulveda-Macias, N. Amigo, and G. Gutiérrez, “Onset of plasticity and its relation to atomic structure in CuZr metallic glass nanowire: A molecular dynamics study,” Journal of Alloys and Compounds. 2016. link Times cited: 17 USED (definite) C. Li, Y. Wei, and X. Shi, “Reformation Capability of Short-Range Order and Their Medium-Range Connections Regulates Deformability of Bulk Metallic Glasses,” Scientific Reports. 2015. link Times cited: 4 USED (definite) Z. W. Wu, F. Li, C. Huo, M. Li, W. Wang, and K. Liu, “Critical scaling of icosahedral medium-range order in CuZr metallic glass-forming liquids,” Scientific Reports. 2015. link Times cited: 32 USED (definite) M. Khandpekar, A. Shrivastava, D. Gowtam, M. Mohape, and V. Deshmukh, “Prediction of glass forming ability in Cu xzr 1-x alloys using molecular dynamics.” 2015. link Times cited: 1 Abstract: Binary CuxZr1−x (x = 0.46, 0.50, 0.58, 0.62) alloy systems w… read more USED (high confidence) S. Sayad, M. Khanzadeh, G. Alahyarizadeh, and N. Amigo, “A molecular dynamics study on the mechanical response of thermal-pressure rejuvenated CuxZr100−x metallic glasses,” Scientific Reports. 2023. link Times cited: 0 USED (high confidence) Y.-T. Sun et al., “Distinct relaxation mechanism at room temperature in metallic glass,” Nature Communications. 2023. link Times cited: 4 USED (high confidence) K. E. Avila, S. Küchemann, R. Pinzón, and H. Urbassek, “Influence of stoichiometry on indentation-induced plasticity in CuZr glasses,” Applied Physics A. 2021. link Times cited: 3 USED (high confidence) Y. Zhang, J. Li, H. Zhou, Y. Hu, S. Ding, and R. Xia, “Cold welding behavior of metallic glass nanowires: Insights from large-scale numerical simulations,” Journal of Materials Science. 2021. link Times cited: 10 USED (high confidence) K. E. Avila, V. Vardanyan, and H. Urbassek, “Transition to chip serration in simulated cutting of metallic glasses,” The European Physical Journal B. 2021. link Times cited: 3 USED (high confidence) A. Abdelmawla, T. Phan, L. Xiong, and A. Bastawros, “A combined experimental and computational analysis on how material interface mediates plastic flow in amorphous/crystalline composites,” Journal of Materials Research. 2021. link Times cited: 3 Abstract: In this work, we study the deformation behavior in amorphous… read more USED (high confidence) W. Wu, D. Şopu, and J. Eckert, “Molecular Dynamics Study of the Nanoindentation Behavior of Cu64Zr36/Cu Amorphous/Crystalline Nanolaminate Composites,” Materials. 2021. link Times cited: 10 Abstract: Amorphous/crystalline nanolaminate composites have aroused e… read more USED (high confidence) S. Zhang, W. Wang, and P. Guan, “Dynamic Crossover in Metallic Glass Nanoparticles*,” Chinese Physics Letters. 2021. link Times cited: 3 USED (high confidence) X. Zhou, L. Wang, and C. Chen, “Atomistic investigation of mechanical properties of metallic glass nanocomposites,” Modelling and Simulation in Materials Science and Engineering. 2020. link Times cited: 1 Abstract: In this paper, tensile deformation of metallic glass (MG) na… read more USED (high confidence) J. Ma, H. Y. Song, J. Y. Wang, J. Dai, and Y. L. Li, “Influence of composition on the mechanical properties of metallic nanoglasses: Insights from molecular dynamics simulation,” Journal of Applied Physics. 2020. link Times cited: 3 Abstract: The introduction of a glass–glass interface is an effective … read more USED (high confidence) G. Mahmud, H. Zhang, and J. Douglas, “Localization model description of the interfacial dynamics of crystalline Cu and Cu64Zr36 metallic glass films.,” The Journal of chemical physics. 2020. link Times cited: 7 Abstract: Recent studies of structural relaxation in Cu-Zr metallic gl… read more USED (high confidence) X. Bian et al., “Signature of local stress states in the deformation behavior of metallic glasses,” NPG Asia Materials. 2020. link Times cited: 33 USED (high confidence) W. Wu, D. Şopu, X. Yuan, and J. Eckert, “Aspect ratio-dependent nanoindentation behavior of Cu64Zr36 metallic glass nanopillars investigated by molecular dynamics simulations,” Journal of Applied Physics. 2020. link Times cited: 8 Abstract: In this paper, we study nanoindentation in Cu64Zr36 metallic… read more USED (high confidence) Z. Wu and R. Li, “Revisiting the breakdown of Stokes-Einstein relation in glass-forming liquids with machine learning,” Science China Physics, Mechanics & Astronomy. 2020. link Times cited: 3 USED (high confidence) K. E. Avila, S. Küchemann, I. A. Alhafez, and H. Urbassek, “An atomistic study of shear-band formation during cutting of metallic glasses,” Journal of Applied Physics. 2020. link Times cited: 17 Abstract: Using molecular dynamics simulations, we study the generatio… read more USED (high confidence) C. Wu and R.-E. Li, “Effects of alloy composition, cavity aspect ratio, and temperature of imprinted ZrCu metallic glass films: a molecular dynamics study,” Applied Physics A. 2020. link Times cited: 7 USED (high confidence) C. Wu and R.-E. Li, “Effects of alloy composition, cavity aspect ratio, and temperature of imprinted ZrCu metallic glass films: a molecular dynamics study,” Applied Physics A. 2020. link Times cited: 0 USED (high confidence) M.-fei Li, B. Liao, Y. Wang, and L. Yang, “Structural mechanisms of the high glass-forming ability in CuZrTiPd metallic glass,” Journal of Materials Science. 2019. link Times cited: 3 USED (high confidence) Z. Chen et al., “Chiral metallic glass nanolattices with combined lower density and improved auxeticity.,” Physical chemistry chemical physics : PCCP. 2019. link Times cited: 6 Abstract: Auxetic materials are promising structural and functional ca… read more USED (high confidence) K. E. Avila, S. Kuchemann, and H. Urbassek, “Stucture and size of the plastic zone formed during nanoindentation of a metallic glass,” Journal of Non-Crystalline Solids. 2019. link Times cited: 9 USED (high confidence) K. E. Avila, S. Kuchemann, I. A. Alhafez, and H. Urbassek, “Nanoscratching of metallic glasses – An atomistic study,” Tribology International. 2019. link Times cited: 42 USED (high confidence) Q. Zhang, Q. Li, S. Zhao, W. Wang, and M. Li, “Structural characteristics in deformation mechanism transformation in nanoscale metallic glasses,” Journal of Physics: Condensed Matter. 2019. link Times cited: 1 Abstract: Deformation of metallic glasses is closely related to their … read more USED (high confidence) Y. Zhang et al., “Atomic-level crystallization in selective laser melting fabricated Zr-based metallic glasses.,” Physical chemistry chemical physics : PCCP. 2019. link Times cited: 16 Abstract: As a promising additive manufacturing technique, selective l… read more USED (high confidence) B. Cheng and J. Trelewicz, “Interfacial plasticity governs strain delocalization in metallic nanoglasses,” Journal of Materials Research. 2019. link Times cited: 12 Abstract: Intrinsic size effects in nanoglass plasticity have been con… read more USED (high confidence) F. Chen and D. Xu, “3D surface condensation of large atomic shear strain in nanoscale metallic glasses under low uniaxial stress,” Journal of Physics: Condensed Matter. 2018. link Times cited: 1 Abstract: Nanoscale metallic glasses (MGs) are frequently used in expe… read more USED (high confidence) Z. Ling, X. Huang, and L. Dai, “Probe Embryonic Damage Evolution in Bulk Metallic Glasses under Plate-impact Loading.” 2018. link Times cited: 1 Abstract: Microdamage in very short stress durations of spallation pro… read more USED (high confidence) Z. Wu, W. Kob, W.-H. Wang, and L. Xu, “Stretched and compressed exponentials in the relaxation dynamics of a metallic glass-forming melt,” Nature Communications. 2018. link Times cited: 47 USED (high confidence) S. Scudino et al., “Ductile bulk metallic glass by controlling structural heterogeneities,” Scientific Reports. 2018. link Times cited: 42 USED (high confidence) B. Demaske, S. Phillpot, and D. Spearot, “Atomic-level deformation of CuxZr100-x metallic glasses under shock loading,” Journal of Applied Physics. 2018. link Times cited: 18 Abstract: Plastic deformation mechanisms in CuxZr100-x bulk metallic g… read more USED (high confidence) Y. F. Wang, H. Y. Li, and L. Yang, “Radiation-induced structural evolution in Zr2Cu metallic glass,” Journal of Materials Science. 2018. link Times cited: 17 USED (high confidence) P. Wen, B. Demaske, D. Spearot, and S. Phillpot, “Shock compression of CuxZr100−x metallic glasses from molecular dynamics simulations,” Journal of Materials Science. 2018. link Times cited: 21 USED (high confidence) L. Yang et al., “Structural responses of metallic glasses under neutron irradiation,” Scientific Reports. 2017. link Times cited: 27 USED (high confidence) B. Liao, S.-yang Wu, and L. Yang, “Free volume: An indicator of the glass-forming ability in binary alloys,” AIP Advances. 2017. link Times cited: 6 Abstract: As a specific concept, free volume is proposed to affect the… read more USED (high confidence) X. Zhao, C. Wang, H. Zheng, Z.-an Tian, and L. Hu, “The role of liquid-liquid transition in glass formation of CuZr alloys.,” Physical chemistry chemical physics : PCCP. 2017. link Times cited: 37 Abstract: Some glass-forming liquids have different liquid phases that… read more USED (high confidence) W. Jian, L. Wang, B. Li, X. Yao, and S. Luo, “Improved ductility of Cu64Zr36 metallic glass/Cu nanocomposites via phase and grain boundaries,” Nanotechnology. 2016. link Times cited: 27 Abstract: We investigate tensile deformation of metallic glass/crystal… read more USED (high confidence) W. Jian, X. Yao, L. Wang, X. C. Tang, and S. Luo, “Short- and medium-range orders in Cu46Zr54 metallic glasses under shock compression,” Journal of Applied Physics. 2015. link Times cited: 26 Abstract: We investigate short- and medium-range orders in Cu46Zr54 me… read more USED (high confidence) Q. Zhang, Q. Li, and M. Li, “Internal stress and its effect on mechanical strength of metallic glass nanowires,” Acta Materialia. 2015. link Times cited: 20 USED (high confidence) D. Şopu and K. Albe, “Influence of grain size and composition, topology and excess free volume on the deformation behavior of Cu–Zr nanoglasses,” Beilstein Journal of Nanotechnology. 2015. link Times cited: 44 Abstract: The influence of grain size and composition on the mechanica… read more USED (high confidence) X. Huang, Z. Ling, and L. Dai, “Ductile-to-brittle transition in spallation of metallic glasses,” Journal of Applied Physics. 2014. link Times cited: 29 Abstract: In this paper, the spallation behavior of a binary metallic … read more USED (high confidence) S. Chill et al., “EON: software for long time simulations of atomic scale systems,” Modelling and Simulation in Materials Science and Engineering. 2014. link Times cited: 56 Abstract: The EON software is designed for simulations of the state-to… read more USED (high confidence) Y. Zhang, N. Mattern, and J. Eckert, “Strong correlation of atomic thermal motion in the first coordination shell of a Cu-Zr metallic glass,” Applied Physics Letters. 2013. link Times cited: 8 Abstract: We demonstrate a strong correlation of atomic thermal motion… read more USED (high confidence) Z. W. Wu, M. Li, W.-Q. Wang, W. Song, and K. Liu, “Effect of local structures on structural evolution during crystallization in undercooled metallic glass-forming liquids.,” The Journal of chemical physics. 2013. link Times cited: 18 Abstract: The effect of local structures on structural evolution durin… read more USED (high confidence) Y. Ritter and K. Albe, “Chemical and topological order in shear bands of Cu64Zr36 and Cu36Zr64 glasses,” Journal of Applied Physics. 2012. link Times cited: 43 Abstract: Shear bands in binary Cu64Zr36 and Cu36Zr64 metallic glasses… read more USED (high confidence) P. Murali, Y. W. Zhang, and H. Gao, “On the characteristic length scales associated with plastic deformation in metallic glasses,” Applied Physics Letters. 2012. link Times cited: 21 Abstract: Atomistic simulations revealed that the spatial correlations… read more USED (high confidence) K. N. Lad, N. Jakse, and A. Pasturel, “Signatures of fragile-to-strong transition in a binary metallic glass-forming liquid.,” The Journal of chemical physics. 2012. link Times cited: 82 Abstract: Classical molecular dynamics investigations of the evolution… read more USED (high confidence) H. Peng, M. Li, W. Wang, C. Wang, and K. Ho, “Effect of local structures and atomic packing on glass forming ability in CuxZr100−x metallic glasses,” Applied Physics Letters. 2010. link Times cited: 174 Abstract: Molecular dynamics simulations are performed for CuZr metall… read more USED (high confidence) Y. Sun, J. Shen, and A. A. Valladares, “Atomic structure and diffusion in Cu60Zr40 metallic liquid and glass: molecular dynamics simulations,” Journal of Applied Physics. 2009. link Times cited: 33 Abstract: Temperature effects on the structural evolution and diffusiv… read more USED (high confidence) V. K. Sutrakar and D. Mahapatra, “Comment on ‘Pseudoelasticity of Cu–Zr nanowires via stress-induced martensitic phase transformations’ [Appl. Phys. Lett. 95, 021911 (2009)],” Applied Physics Letters. 2009. link Times cited: 9 Abstract: Recently, a novel stress-induced phase transformation in an … read more USED (high confidence) D. Şopu, K. Albe, Y. Ritter, and H. Gleiter, “From nanoglasses to bulk massive glasses,” Applied Physics Letters. 2009. link Times cited: 78 Abstract: Molecular dynamics simulations are presented that provide ev… read more USED (high confidence) M. Mendelev, R. Ott, M. Kramer, and D. Sordelet, “Determining strain in amorphous alloys: Uncertainties with analyzing structural changes during deformation,” Journal of Applied Physics. 2009. link Times cited: 1 Abstract: Molecular dynamics simulations were utilized to test the rel… read more USED (high confidence) M. Mendelev, D. Rehbein, R. Ott, M. Kramer, and D. Sordelet, “Computer simulation and experimental study of elastic properties of amorphous Cu-Zr alloys,” Journal of Applied Physics. 2007. link Times cited: 57 Abstract: Molecular-dynamics simulations were performed to determine t… read more USED (high confidence) N. Fayzullayev, J. Kurbonov, L. U. Uktamov, R. J. Kurbonova, and J. Kurbonov, “The effect of reagents on the production of highly nanocomposite bentonite sorbents using zol-gel technology,” E3S Web of Conferences. 2023. link Times cited: 0 Abstract: In this study, the analysis of the study of the effect of re… read more USED (high confidence) A. Anggono et al., “Combined Effects of Annealing and Cyclic Loading on Structural Rejuvenation and Mechanical Properties of CuZr Metallic Glass: A Molecular Dynamics Study,” Materials Research. 2022. link Times cited: 3 Abstract: 2021 Structural rejuvenation is one of the key topics in the… read more USED (high confidence) Y.-chen Cui, Y. Shibutani, P. Huang, F. Wang, K. Xu, and T. Lu, “Interface-Related Shear Banding Deformation of Amorphous/Crystalline CuZr/Cu Nanolaminates by Molecular Dynamics Simulations,” Materials Transactions. 2017. link Times cited: 1 Abstract: 1State-key Laboratory for Mechanical Behavior of Material, X… read more USED (high confidence) L. Dai, X. Huang, and Z. Ling, “Cavitation instability in bulk metallic glasses.” 2015. link Times cited: 0 Abstract: Recent experiments have shown that fracture surfaces of hulk… read more USED (high confidence) S. Biwa, S. Kishiwada, C. Inserra, and E. Matsumoto, “Modeling of Flexural Wave Propagation in a Plate with Contacting Interfaces,” Journal of Solid Mechanics and Materials Engineering. 2010. link Times cited: 5 Abstract: Propagation characteristics of a flexural wave in a thin pla… read more USED (low confidence) A. Agrawal, S. Bakhtiari, R. Mirzaeifar, D. Jiang, H. Yang, and Y. Liu, “A comparative study of the amorphization of NiTi-B2 structure by anti-site defects,” Journal of Alloys and Compounds. 2024. link Times cited: 0 USED (low confidence) W. Song, Y. Meng, L. Xiao, and S. Liu, “Tuning dynamic mechanical properties of Cu50Zr50 nanoglasses/ nanopolycrystalline Cu composites investigated by molecular dynamics simulation,” Journal of Non-Crystalline Solids. 2024. link Times cited: 0 USED (low confidence) H. Ma et al., “Roots seeking of multiple shear-bands in amorphous alloys at the atomic scale,” Journal of Non-Crystalline Solids. 2024. link Times cited: 0 USED (low confidence) X. Fu et al., “The innate interfacial elastic strain field of a transformable B2 precipitate embedded in an amorphous matrix,” npj Computational Materials. 2023. link Times cited: 0 USED (low confidence) Y. Luo, J. Huang, X. Yu, G. Liu, S. Cao, and D. Fan, “The effect of crystalline structure on the mechanical behavior in Zr-based amorphous materials: A molecular dynamics simulation,” Journal of Non-Crystalline Solids. 2023. link Times cited: 0 USED (low confidence) K. E. Avila, V. Vardanyan, T. Zhu, S. Küchemann, M. Smaga, and H. Urbassek, “Plasticity in cyclic indentation of a Cu-Zr-based bulk metallic glass after tensile loading: An experimental and molecular dynamics simulation study,” Journal of Non-Crystalline Solids. 2023. link Times cited: 1 USED (low confidence) Z. Zhou et al., “Effect of precipitate shape and distribution on mechanical behavior of shape memory metallic glass composites by molecular dynamics method,” Journal of Alloys and Compounds. 2023. link Times cited: 0 USED (low confidence) J. Xi, F. Yang, X. Zhang, and H. Zhou, “Effect of geometry of crystalline dendrite on the uniaxial tension behavior of metallic glass matrix composites based on molecular dynamics simulations,” Materials Today Communications. 2023. link Times cited: 0 USED (low confidence) Y. Liu et al., “Investigations into the effect of cutting speed on nano-cutting of metallic glass by using molecular dynamics simulation analysis,” The International Journal of Advanced Manufacturing Technology. 2023. link Times cited: 1 USED (low confidence) P. Hopur, W. Chen, Y. Zhou, J. Zhou, and T. Wang, “The Correlation among the Atomic Structure, Electronic Valence Band and Properties of Zr-Cu-Al-Ag Bulk Metallic Glasses,” Metals. 2023. link Times cited: 0 Abstract: Investigating the relationship between the glass-forming abi… read more USED (low confidence) X. Cui et al., “Investigations into effect of tool rake angle on nanocutting process for Zr-based amorphous alloy by molecular dynamics simulation,” The International Journal of Advanced Manufacturing Technology. 2023. link Times cited: 0 USED (low confidence) P. Garg and T. Rupert, “Local structural ordering determines the mechanical damage tolerance of amorphous grain boundary complexions,” Scripta Materialia. 2023. link Times cited: 0 USED (low confidence) X. Kong, W. Wang, M. Wang, and N. Hou, “Nanocutting mechanisms of Cu50Zr50 amorphous alloy: A molecular dynamics simulation,” Journal of Non-Crystalline Solids. 2023. link Times cited: 2 USED (low confidence) Y.-li Li, W. Wu, D. Şopu, and J. Eckert, “Effects of void shape and location on the fracture and plastic deformation of Cu (crystalline) /Cu64Zr36 (amorphous) composites,” Journal of Materials Research and Technology. 2023. link Times cited: 2 USED (low confidence) Y. Tang and H. Zhou, “High pressure heat treatment tuning cavitation behavior in FeP metallic glass,” Acta Mechanica Sinica. 2023. link Times cited: 0 USED (low confidence) W. H. Ryu et al., “Sustainable steady-state serrated flow induced by modulating deformation sequence in bulk metallic glass,” Journal of Alloys and Compounds. 2023. link Times cited: 2 USED (low confidence) B. Waters, D. S. Karls, I. Nikiforov, R. Elliott, E. Tadmor, and B. Runnels, “Automated determination of grain boundary energy and potential-dependence using the OpenKIM framework,” Computational Materials Science. 2022. link Times cited: 5 USED (low confidence) A.-S. Tran, D.-Q. Doan, and V. Chu, “Molecular simulation study on mechanical properties and elastic recovery of nanoimprinted CuAgAu metallic glasses,” Journal of Non-Crystalline Solids. 2022. link Times cited: 4 USED (low confidence) Z. Xie, Y. Zhang, S. Huang, Z. Li, Q. Cheng, and J. Zhou, “Towards quantitative determination of atomic structures of amorphous materials in three dimensions,” National Science Open. 2022. link Times cited: 1 Abstract: : Amorphous materials such as glass, polymer and amorphous a… read more USED (low confidence) L. Zhang et al., “Shear-band blunting governs superior mechanical properties of shape memory metallic glass composites,” Acta Materialia. 2022. link Times cited: 9 USED (low confidence) D. Şopu et al., “Rejuvenation engineering in metallic glasses by complementary stress and structure modulation,” NPG Asia Materials. 2022. link Times cited: 1 USED (low confidence) L.-li Zhou et al., “Topologically close-packed structure characteristics of the plastic deformation regions of amorphous Cu64.5Zr35.5,” Journal of Materials Research and Technology. 2022. link Times cited: 2 USED (low confidence) Y. Zhang, J. Xu, Y. Hu, S. Ding, and R. Xia, “Cold welding of ultrathin metallic glass nanowires with side-to-side contact using molecular dynamics simulations,” Materials Today Communications. 2022. link Times cited: 4 USED (low confidence) C. Liu, S. Yuan, J. Im, F. D. de Barros, S. Masri, and P. S. Branicio, “Mechanical Properties, Failure Mechanisms, and Scaling Laws of Bicontinuous Nanoporous Metallic Glasses,” Acta Materialia. 2022. link Times cited: 7 USED (low confidence) I. Patra, A. Abdulhadi, F. S. Fahim, B. S. Bashar, T. Alawsi, and M. Salmani, “The Effects of Temperature and Impact Velocity on the Shock Wave Response of Pore-Embedded Metallic Glasses,” Advances in Materials Science and Engineering. 2022. link Times cited: 2 Abstract: In this work, the shock wave response of a pore-embedded CuZ… read more USED (low confidence) W. Wu, Z.-S. Peng, D. Şopu, and J. Eckert, “Molecular dynamics study of fracture and plastic deformation of Cu/Cu64Zr36 crystalline/amorphous composites with a pre-existing void,” Journal of Non-Crystalline Solids. 2022. link Times cited: 4 USED (low confidence) G. Wei, J. Cui, W. Wang, X. Guo, J. Ren, and W. Wang, “Short-to-medium range structure and glass-forming ability in metallic glasses,” Physical Review Materials. 2022. link Times cited: 0 USED (low confidence) Y. Zhang, M. Cheng, L. Meng, and X. Yao, “Microstructural evolution of shear bands formation of metallic glasses under different loading conditions and strain rates,” Journal of Non-Crystalline Solids. 2022. link Times cited: 3 USED (low confidence) J. Zhang, X. Wang, M. Zhang, L. Deng, and P. Gong, “The shock forming process of Cu50Zr50 metallic glasses studied via molecular dynamics simulation,” Journal of Non-Crystalline Solids. 2022. link Times cited: 6 USED (low confidence) D. Bokov et al., “The effects of initial rejuvenation on the cold joining behavior of Cu60Zr40 metallic glass,” Applied Physics A. 2022. link Times cited: 2 USED (low confidence) G. Katakareddi and N. Yedla, “The effect of loading methods on the microstructural evolution and degree of strain localization in Cu50Zr50 metallic glass composite nanowires: A molecular dynamics simulation study.,” Journal of molecular graphics & modelling. 2022. link Times cited: 1 USED (low confidence) M. Müser, S. Sukhomlinov, and L. Pastewka, “Interatomic potentials: achievements and challenges,” Advances in Physics: X. 2022. link Times cited: 12 Abstract: ABSTRACT Interatomic potentials approximate the potential en… read more USED (low confidence) X. Yuan et al., “Maximizing the degree of rejuvenation in metallic glasses,” Scripta Materialia. 2022. link Times cited: 14 USED (low confidence) A. Abed et al., “The Characterization of Cold Welding Process in CuZr Metallic Glasses with Dissimilar Alloying Compositions,” Materials Today Communications. 2022. link Times cited: 4 USED (low confidence) X. Yuan, D. Şopu, K. Song, and J. Eckert, “Relaxation and Strain-Hardening Relationships in Highly Rejuvenated Metallic Glasses,” Materials. 2022. link Times cited: 6 Abstract: One way to rejuvenate metallic glasses is to increase their … read more USED (low confidence) N. Amigo and F. Valencia, “Species Content Effect on the Rejuvenation Degree of CuZr Metallic Glasses Under Thermal-Pressure Treatments,” Metals and Materials International. 2022. link Times cited: 4 USED (low confidence) Y. Zhang, J. Li, Q. Zhang, S. Ding, W. Wu, and R. Xia, “Tetrachiral nanostructured metallic glasses with mechanically tunable performance,” Materials Chemistry and Physics. 2022. link Times cited: 3 USED (low confidence) T. Zhao, H. Song, M. An, and M. Xiao, “Effect of graphene on the mechanical properties of metallic glasses: Insight from molecular dynamics simulation,” Materials Chemistry and Physics. 2022. link Times cited: 3 USED (low confidence) S. Chupradit et al., “Role of Glass Composition on Mechanical Properties of Shape Memory Alloy-Metallic Glass Composites,” Advances in Materials Science and Engineering. 2021. link Times cited: 6 Abstract: In this work, the molecular dynamics (MD) simulation was app… read more USED (low confidence) Y. Zhang, J. Li, Y. Hu, S. Ding, F. Du, and R. Xia, “Characterization of the deformation behaviors under uniaxial stress for bicontinuous nanoporous amorphous alloys.,” Physical chemistry chemical physics : PCCP. 2021. link Times cited: 10 Abstract: In this paper, the deformation behaviors of Cu50Zr50 biconti… read more USED (low confidence) T.-C. Chen et al., “Role of thermal history on atomic structure and ductility of ion-irradiated metallic glasses,” Modelling and Simulation in Materials Science and Engineering. 2021. link Times cited: 0 Abstract: Maximizing the structural rejuvenation and ductility is one … read more USED (low confidence) Y. Tang et al., “Tailoring microstructure of metallic glass for delocalized plasticity by pressure annealing: Forward and inverse studies,” Acta Materialia. 2021. link Times cited: 7 USED (low confidence) A. Agrawal and R. Mirzaeifar, “Computational investigation of deformation mechanisms at the atomistic scale of metallic glass-graphene composites (MGGCs),” Journal of Applied Physics. 2021. link Times cited: 1 USED (low confidence) Y. Zhang, J. Li, Y. Hu, S. Ding, F. Du, and R. Xia, “Mechanical properties and scaling laws of polycrystalline CuZr shape memory alloy,” Journal of Applied Physics. 2021. link Times cited: 5 Abstract: Thanks to their excellent properties such as superelasticity… read more USED (low confidence) A.-S. Tran, “Nanoindentation characteristics and recovery capacity of amorphous CuxTa100-x/Cu crystalline nanolaminates,” Journal of Non-crystalline Solids. 2021. link Times cited: 2 USED (low confidence) G. Katakareddi and N. Yedla, “Creep Behavior of Core (Metal)–Shell (Metallic Glass) Structure: a Molecular Dynamics Simulation Study,” Transactions of the Indian National Academy of Engineering. 2021. link Times cited: 1 USED (low confidence) K. E. Avila, S. Küchemann, and H. Urbassek, “Interaction between parallel shear bands in a metallic glass,” Journal of Non-crystalline Solids. 2021. link Times cited: 13 USED (low confidence) L. Shao, D. Chen, A. Zare, and D. Lucca, “Mechanism of nanocrystallization temperature shifting during ion irradiation of metallic glasses,” Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms. 2021. link Times cited: 2 USED (low confidence) Y. Zhang, Y. Xian, J. Li, S. Ding, S. Liu, and R. Xia, “Atomistic investigation on the mechanical properties of 3D nanoporous metallic glasses under uniaxial tension and compression,” Materials today communications. 2021. link Times cited: 8 USED (low confidence) V. Vardanyan, K. E. Avila, S. Küchemann, and H. Urbassek, “Interaction of dislocations and shear bands in cutting of an amorphous-crystalline bilayer: An atomistic study,” Computational Materials Science. 2021. link Times cited: 10 USED (low confidence) A.-S. Tran, “Strengthening mechanism and plasticity deformation of crystalline/amorphous Cu/CuTa nanomultilayer,” Journal of Non-crystalline Solids. 2021. link Times cited: 6 USED (low confidence) X. Yuan, D. Şopu, and J. Eckert, “Origin of strain hardening in monolithic metallic glasses,” Physical Review B. 2021. link Times cited: 12 USED (low confidence) M. Paramonov, D. Minakov, V. Fokin, D. V. Knyazev, G. S. Demyanov, and P. Levashov, “Ab initio inspection of thermophysical experiments for zirconium near melting,” Journal of Applied Physics. 2021. link Times cited: 3 Abstract: We present quantum molecular dynamics calculations of thermo… read more USED (low confidence) Y. L. Tang et al., “Extra plasticity governed by shear band deflection in gradient metallic glasses,” Nature Communications. 2021. link Times cited: 23 USED (low confidence) G. Mahmud, H. Zhang, and J. Douglas, “Localization model description of the interfacial dynamics of crystalline Cu and [Formula: see text] metallic glass nanoparticles.,” The European physical journal. E, Soft matter. 2021. link Times cited: 2 USED (low confidence) Y. Tang, H. F. Zhou, X. D. Wang, Q. Cao, D. X. Zhang, and J. Jiang, “Origin of different thermal cycling effects in Fe80P20 and Ni60Nb40 metallic glasses,” Materials Today Physics. 2021. link Times cited: 10 USED (low confidence) K. E. Avila, V. Vardanyan, S. Küchemann, and H. Urbassek, “Response of an amorphous/crystalline interface to nanoindentation: an atomistic study,” Applied Surface Science. 2021. link Times cited: 13 USED (low confidence) A.-S. Tran and T. Fang, “The influence of intrinsic size in amorphous CuxTa100-x/Cu crystalline nanolaminates using molecular dynamics simulation,” Physica E-low-dimensional Systems & Nanostructures. 2021. link Times cited: 7 USED (low confidence) C. Liu, S. Yuan, and P. S. Branicio, “Bicontinuous Nanoporous Design Induced Homogenization of Strain Localization in Metallic Glasses,” EngRN: Dynamical System (Topic). 2021. link Times cited: 15 Abstract: Bicontinuous nanoporous metallic glasses (MG) synergize the … read more USED (low confidence) W. Li, H. Y. Song, J. Dai, J. Wang, M. An, and Y. Li, “Effect of shape memory alloys on the mechanical properties of metallic glasses: A molecular dynamics study,” Computational Materials Science. 2021. link Times cited: 9 USED (low confidence) S. Li, P. Huang, and F. Wang, “Achieving pronounced β-relaxations and improved plasticity in CuZr metallic glass,” Journal of Alloys and Compounds. 2021. link Times cited: 2 USED (low confidence) K. E. Avila, V. Vardanyan, I. A. Alhafez, M. Zimmermann, B. Kirsch, and H. Urbassek, “Applicability of cutting theory to nanocutting of metallic glasses: Atomistic simulation,” Journal of Non-crystalline Solids. 2020. link Times cited: 16 USED (low confidence) J. Li et al., “A concurrent high strength and ductility of 3D gyroidal nanoporous metallic glasses,” Journal of Non-crystalline Solids. 2020. link Times cited: 7 USED (low confidence) K. N. Lad and K. Soni, “Effect of Al addition on structure and dynamics of Zr-Cu-Al glass-forming alloy,” Materials Today: Proceedings. 2020. link Times cited: 1 USED (low confidence) J. Ma, H. Y. Song, M. An, W. Li, and R. Han, “A strategy for improving mechanical properties of metallic glass by tailoring interface structure,” Journal of Non-crystalline Solids. 2020. link Times cited: 6 USED (low confidence) A.-S. Tran and T. Fang, “Effects of grain size and indentation sensitivity on deformation mechanism of nanocrystalline tantalum,” International Journal of Refractory Metals & Hard Materials. 2020. link Times cited: 6 USED (low confidence) A.-S. Tran and T. Fang, “Size effect and interfacial strength in nanolaminated Cu/CuxTa100-x composites using molecular dynamics,” Computational Materials Science. 2020. link Times cited: 12 USED (low confidence) T. Dutta, A. Chauniyal, I. Singh, and R. Narasimhan, “Numerical investigation of tensile response of notched bulk metallic glass composite specimens,” Modelling and Simulation in Materials Science and Engineering. 2020. link Times cited: 3 Abstract: In this work, plane strain finite element and atomistic simu… read more USED (low confidence) Z. Xie, W. Jian, X. Tang, X. Zhang, and X. Yao, “Strengthening and toughening mechanisms of metallic glass nanocomposites via graphene nanoplatelets,” Journal of Non-crystalline Solids. 2020. link Times cited: 4 USED (low confidence) H. Y. Song, B. Duan, Y. Wang, M. An, and Y. L. Li, “Enhanced plasticity by introducing amorphous phase in nanopolycrystal Cu: A molecular dynamics study,” Materials Chemistry and Physics. 2020. link Times cited: 4 USED (low confidence) Q. Zhang, Q. Li, and M. Li, “From deformation localization to melting and chemical segregation in metallic glass nanoparticles under high strain rate,” Journal of Applied Physics. 2020. link Times cited: 0 Abstract: Nanoparticles possess many distinguished properties due to t… read more USED (low confidence) A.-S. Tran, “Phase transformation and interface fracture of Cu/Ta multilayers: A molecular dynamics study,” Engineering Fracture Mechanics. 2020. link Times cited: 16 USED (low confidence) S. Yuan, X. Song, and P. S. Branicio, “Tuning the Mechanical Properties of Shape Memory Metallic Glass Composites with Brick and Mortar Designs,” Scripta Materialia. 2020. link Times cited: 18 USED (low confidence) B. Fan, K. Han, H. P. Zhang, and M. Li, “Low-frequency vibrational properties and structure correlation in metallic glass,” Journal of Non-crystalline Solids. 2020. link Times cited: 0 USED (low confidence) J. Houška, P. Machanova, M. Zítek, and P. Zeman, “Molecular dynamics and experimental study of the growth, structure and properties of Zr–Cu films,” Journal of Alloys and Compounds. 2020. link Times cited: 11 USED (low confidence) D.-Q. Doan, T. Fang, and T.-H. Chen, “Nanotribological characteristics and strain hardening of amorphous Cu64Zr36/ crystalline Cu nanolaminates,” Tribology International. 2020. link Times cited: 36 USED (low confidence) M. Wang, H. Liu, J. Li, Q. Jiang, W. Yang, and C. Tang, “Thermal-pressure treatment for tuning the atomic structure of metallic glass Cu-Zr,” Journal of Non-crystalline Solids. 2020. link Times cited: 12 USED (low confidence) Z. Xie, W. Jian, Z. Wang, X. Zhang, and X. Yao, “Layer thickness effects on the strengthening and toughening mechanisms in metallic glass-graphene nanolaminates,” Computational Materials Science. 2020. link Times cited: 17 USED (low confidence) R. Jana, J. von Lautz, S. M. Khosrownejad, W. Andrews, M. Moseler, and L. Pastewka, “Constitutive relations for plasticity of amorphous carbon,” Journal of Physics: Materials. 2020. link Times cited: 5 Abstract: We deform representative volume elements of amorphous carbon… read more USED (low confidence) D. Şopu, S. Scudino, X. L. Bian, C. Gammer, and J. Eckert, “Atomic-scale origin of shear band multiplication in heterogeneous metallic glasses,” Scripta Materialia. 2020. link Times cited: 74 USED (low confidence) D.-Q. Doan, T. Fang, A.-S. Tran, and T.-H. Chen, “High deformation capacity and dynamic shear band propagation of imprinted amorphous Cu50Zr50/crystalline Cu multilayered nanofilms,” Journal of Physics and Chemistry of Solids. 2020. link Times cited: 23 USED (low confidence) J. Mo, H. Liu, Z. Chen, Y. Z. He, W. Yang, and B. Shen, “Estimation of the glass-forming ability of metallic glasses with monolayer two-dimensional model,” Computational Materials Science. 2020. link Times cited: 0 USED (low confidence) D.-Q. Doan, T. Fang, A.-S. Tran, and T.-H. Chen, “Residual stress and elastic recovery of imprinted Cu-Zr metallic glass films using molecular dynamic simulation,” Computational Materials Science. 2019. link Times cited: 46 USED (low confidence) L. Chen et al., “Correlation of viscosity with atomic packing in Cu50Zr50 melt,” Journal of Molecular Liquids. 2019. link Times cited: 9 USED (low confidence) A.-S. Tran and T. Fang, “Void growth and coalescence in Cu-Ta metallic glasses using molecular dynamics,” Computational Materials Science. 2019. link Times cited: 21 USED (low confidence) X. Zhou, L. Wang, and C. Chen, “Improving ductility of nanoporous metallic glasses,” Computational Materials Science. 2019. link Times cited: 15 USED (low confidence) S. Li, P. Huang, and F. Wang, “Rejuvenation saturation upon cyclic elastic loading in metallic glass,” Computational Materials Science. 2019. link Times cited: 21 USED (low confidence) K. Kosiba, D. Şopu, S. Scudino, L. Zhang, J. Bednarčík, and S. Pauly, “Modulating heterogeneity and plasticity in bulk metallic glasses: Role of interfaces on shear banding,” International Journal of Plasticity. 2019. link Times cited: 76 USED (low confidence) D. Zhao, S. Wang, B. Zhu, L. Li, and H. Zhao, “Anisotropic deformation behaviors of amorphous-crystalline nanolaminates investigated via molecular dynamics simulations,” Journal of Alloys and Compounds. 2019. link Times cited: 10 USED (low confidence) B. Cheng and J. Trelewicz, “Controlling interface structure in nanoglasses produced through hydrostatic compression of amorphous nanoparticles,” Physical Review Materials. 2019. link Times cited: 12 Abstract: Controlling glass-glass interfaces in metallic nanoglasses i… read more USED (low confidence) S. Ketov et al., “High-resolution transmission electron microscopy investigation of diffusion in metallic glass multilayer films,” Materials Today Advances. 2019. link Times cited: 13 USED (low confidence) H. Y. Song, M. Wang, M. An, and Y. L. Li, “Enhancing the plasticity of noncrystalline Cu Zr multilayer: Insights from molecular dynamics simulations,” Journal of Non-Crystalline Solids. 2019. link Times cited: 5 USED (low confidence) H. Song, J. J. Xu, Q. Deng, and Y. Li, “Effect of interface structure on deformation behavior of crystalline Cu/amorphous CuZr sandwich structures,” Physics Letters A. 2019. link Times cited: 8 USED (low confidence) M. Wang et al., “Thermal-pressure effects on energy state of metallic glass Cu50Zr50,” Computational Materials Science. 2018. link Times cited: 17 USED (low confidence) W. Jian, L. Wang, X. Yao, and S. Luo, “Tensile and nanoindentation deformation of amorphous/crystalline nanolaminates: Effects of layer thickness and interface type,” Computational Materials Science. 2018. link Times cited: 28 USED (low confidence) H. N. Pishkenari, F. S. Yousefi, and A. Taghibakhshi, “Determination of surface properties and elastic constants of FCC metals: a comparison among different EAM potentials in thin film and bulk scale,” Materials Research Express. 2018. link Times cited: 22 Abstract: Three independent elastic constants C11, C12, and C44 were c… read more USED (low confidence) K. Zhou, T. Zhang, B. Liu, and Y. Yao, “Atomistic simulations of the effect of Zr addition on the microstructure and plastic deformation of nanocrystalline copper,” Physica B: Condensed Matter. 2018. link Times cited: 2 USED (low confidence) D. Şopu, K. Albe, and J. Eckert, “Metallic glass nanolaminates with shape memory alloys,” Acta Materialia. 2018. link Times cited: 38 USED (low confidence) J. Feng, P. Chen, and M. Li, “Existence of fractal packing in metallic glasses: Molecular dynamics simulations ofCu46Zr54,” Physical Review B. 2018. link Times cited: 7 USED (low confidence) Y. Zhang et al., “Atomic-scale structural evolution in selective laser melting of Cu50Zr50 metallic glass,” Computational Materials Science. 2018. link Times cited: 30 USED (low confidence) B. Cheng and J. Trelewicz, “Design of crystalline-amorphous nanolaminates using deformation mechanism maps,” Acta Materialia. 2018. link Times cited: 34 USED (low confidence) H. Y. Song, S. Li, M. An, Q. Deng, and Y. L. Li, “Effect of crystal phase on shear bands initiation and propagation behavior in metallic glass matrix composites,” Computational Materials Science. 2018. link Times cited: 9 USED (low confidence) H. Y. Song, M. Wang, Q. Deng, and Y. L. Li, “Deformation mode transitions in Cu 50 Zr 50 amorphous/Cu crystalline nanomultilayer: A molecular dynamics study,” Journal of Non-Crystalline Solids. 2018. link Times cited: 21 USED (low confidence) C. Wu and C. Hou, “Molecular dynamics analysis of plastic deformation and mechanics of imprinted metallic glass films,” Computational Materials Science. 2018. link Times cited: 23 USED (low confidence) M. Sepulveda-Macias, N. Amigo, and G. Gutiérrez, “Tensile behavior of Cu 50 Zr 50 metallic glass nanowire with a B2 crystalline precipitate,” Physica B-condensed Matter. 2018. link Times cited: 21 USED (low confidence) T. Dutta, A. Chauniyal, I. Singh, R. Narasimhan, T. P. G. Thamburaja, and U. Ramamurty, “Plastic deformation and failure mechanisms in nano-scale notched metallic glass specimens under tensile loading,” Journal of The Mechanics and Physics of Solids. 2018. link Times cited: 33 USED (low confidence) B. Wang, G. Kang, Q. Kan, W. Wu, K. Zhou, and C. Yu, “Atomistic study on the super-elasticity of single crystal bulk NiTi shape memory alloy under adiabatic condition,” Computational Materials Science. 2018. link Times cited: 24 USED (low confidence) J. Yu, M. Wang, and S. Lin, “Slower icosahedral cluster rejuvenation drives the brittle-to-ductile transition in nanoscale metallic glasses,” Computational Materials Science. 2017. link Times cited: 17 USED (low confidence) H. Y. Song, S. Li, and Q. Deng, “Coupling effects of thickness and aspect ratio on deformation behavior of Cu50Zr50 metallic glass,” Computational Materials Science. 2017. link Times cited: 26 USED (low confidence) M. Kozłowski, D. Scopece, J. Janczak-Rusch, L. Jeurgens, R. Abdank-Kozubski, and D. Passerone, “Validation of an Embedded-Atom Copper Classical Potential via Bulk and Nanostructure Simulations,” Diffusion Foundations. 2017. link Times cited: 0 Abstract: The validation of classical potentials for describing multic… read more USED (low confidence) H. Y. Song, S. Li, Y. G. Zhang, Q. Deng, T. H. Xu, and Y. L. Li, “Atomic simulations of plastic deformation behavior of Cu 50 Zr 50 metallic glass,” Journal of Non-crystalline Solids. 2017. link Times cited: 29 USED (low confidence) H. Y. Song, J. Xu, Y. G. Zhang, S. Li, D. Wang, and Y. L. Li, “Molecular dynamics study of deformation behavior of crystalline Cu/amorphous Cu50Zr50 nanolaminates,” Materials & Design. 2017. link Times cited: 58 USED (low confidence) C. Zhong, Q. Cao, X. Wang, D. Zhang, H. Fecht, and J. Jiang, “Relationship of deformation mode with strain-dependent shear transformation zone size in Cu-Zr metallic glasses using molecular dynamics simulations,” Journal of Non-crystalline Solids. 2017. link Times cited: 8 USED (low confidence) B. Ding and X. Li, “An Eccentric Ellipse Failure Criterion for Amorphous Materials,” Journal of Applied Mechanics. 2017. link Times cited: 7 USED (low confidence) T. W. Wu et al., “The compressive behaviour after crystallisation in Zr85Cu15 metallic glasses studied by molecular dynamics simulations,” Journal of Non-crystalline Solids. 2017. link Times cited: 5 USED (low confidence) L. Lang et al., “Molecular dynamics simulations of the structure evolutions of Cu-Zr metallic glasses under irradiation,” Nuclear Instruments & Methods in Physics Research Section B-beam Interactions With Materials and Atoms. 2017. link Times cited: 9 USED (low confidence) Y.-chen Cui, Y. Shibutani, S. Li, P. Huang, and F. Wang, “Plastic deformation behaviors of amorphous-Cu50Zr50/crystalline-Cu nanolaminated structures by molecular dynamics simulations,” Journal of Alloys and Compounds. 2017. link Times cited: 42 USED (low confidence) Q. Zhang, Q. Li, and M. Li, “Key factors affecting mechanical behavior of metallic glass nanowires,” Scientific Reports. 2017. link Times cited: 19 USED (low confidence) S. Pan, Z. W. Wu, W.-chao Wang, M. Li, and L. Xu, “Structural origin of fractional Stokes-Einstein relation in glass-forming liquids,” Scientific Reports. 2017. link Times cited: 27 USED (low confidence) C. Zhong et al., “Deformation behavior of metallic glasses with shear band like atomic structure: a molecular dynamics study,” Scientific Reports. 2016. link Times cited: 40 USED (low confidence) C. Zhong et al., “Size distribution of shear transformation zones and. their evolution towards the formation of shear bands in metallic glasses,” Journal of Non-crystalline Solids. 2016. link Times cited: 22 USED (low confidence) W. Zhao, C. Jialin, S. Feng, G. Li, and R. Liu, “Intrinsic correlation between elastic modulus and atomic bond stiffness in metallic glasses,” Materials Letters. 2016. link Times cited: 11 USED (low confidence) D. Şopu, A. Foroughi, M. Stoica, and J. Eckert, “Brittle-to-Ductile Transition in Metallic Glass Nanowires.,” Nano letters. 2016. link Times cited: 84 Abstract: When reducing the size of metallic glass samples down to the… read more USED (low confidence) S. M. Rassoulinejad-Mousavi, Y. Mao, and Y. Zhang, “Evaluation of Copper, Aluminum and Nickel Interatomic Potentials on Predicting the Elastic Properties,” arXiv: Computational Physics. 2016. link Times cited: 63 Abstract: Choice of appropriate force field is one of the main concern… read more USED (low confidence) S. Feng et al., “Structural feature of Cu64Zr36 metallic glass on nanoscale: Densely-packed clusters with loosely-packed surroundings,” Scripta Materialia. 2016. link Times cited: 36 USED (low confidence) C. Zhong et al., “On the critical thickness for non-localized to localized plastic flow transition in metallic glasses: A molecular dynamics study,” Scripta Materialia. 2016. link Times cited: 47 USED (low confidence) S. Chattopadhyay et al., “Local structure, composition, and crystallization mechanism of a model two-phase ‘composite nanoglass’.,” The Journal of chemical physics. 2016. link Times cited: 3 Abstract: We report a detailed study of the local composition and stru… read more USED (low confidence) X. Zhou, H. Zhou, X. Li, and C. Chen, “Size effects on tensile and compressive strengths in metallic glass nanowires,” Journal of The Mechanics and Physics of Solids. 2015. link Times cited: 60 USED (low confidence) D. Wen, P. Peng, Y.-qi Jiang, Z.-an Tian, W. Li, and R.-su Liu, “Correlation of the heredity of icosahedral clusters with the glass forming ability of rapidly solidified CuxZr100 − x alloys,” Journal of Non-crystalline Solids. 2015. link Times cited: 24 USED (low confidence) B. Sun and W. Wang, “The fracture of bulk metallic glasses,” Progress in Materials Science. 2015. link Times cited: 406 USED (low confidence) Z. Trautt, F. Tavazza, and C. Becker, “Facilitating the selection and creation of accurate interatomic potentials with robust tools and characterization,” Modelling and Simulation in Materials Science and Engineering. 2015. link Times cited: 14 Abstract: The Materials Genome Initiative seeks to significantly decre… read more USED (low confidence) L. Gao, S. Feng, L. Qi, F. Zhao, and R. P. Liu, “Effects of nanocrystals on evolution behavior of shear transformation zones in Zr85Cu15 metallic glasses,” Journal of Non-crystalline Solids. 2015. link Times cited: 4 USED (low confidence) J. Luo and Y. Shi, “The local stress state of a running shear band in amorphous solids,” Journal of Materials Research. 2015. link Times cited: 7 Abstract: In molecular dynamics simulations, the local stress state in… read more USED (low confidence) D. Şopu, M. Stoica, and J. Eckert, “Deformation behavior of metallic glass composites reinforced with shape memory nanowires studied via molecular dynamics simulations,” Applied Physics Letters. 2015. link Times cited: 56 Abstract: Molecular dynamics simulations indicate that the deformation… read more USED (low confidence) Y. Mo et al., “Non-linear effects of initial melt temperatures on microstructures and mechanical properties during quenching process of liquid Cu46Zr54 alloy,” Physica B-condensed Matter. 2015. link Times cited: 5 USED (low confidence) C. Zhong, H. Zhang, Q. Cao, W. Xiaodong, D. X. Zhang, and J. Jiang, “The size-dependent non-localized deformation in a metallic alloy,” Scripta Materialia. 2015. link Times cited: 51 USED (low confidence) X. Zhou and C. Chen, “Molecular dynamic simulations of the mechanical properties of crystalline/crystalline and crystalline/amorphous nanolayered pillars,” Computational Materials Science. 2015. link Times cited: 18 USED (low confidence) Y. Mo et al., “Formation and evolution of nano-clusters in a large-scale system of Cu–Zr alloy during rapid solidification process,” Computational Materials Science. 2015. link Times cited: 14 USED (low confidence) Y. Hu, D. Wen, Y.-qi Jiang, Y. Deng, and P. Peng, “Effect of cooling rates on clustering towards icosahedra in rapidly solidified Cu56Zr44 alloy,” Transactions of Nonferrous Metals Society of China. 2015. link Times cited: 6 USED (low confidence) Y. Hiraoka, T. Nakamura, A. Hirata, E. G. Escolar, K. Matsue, and Y. Nishiura, “Hierarchical structures of amorphous solids characterized by persistent homology,” Proceedings of the National Academy of Sciences. 2015. link Times cited: 253 Abstract: Significance Persistent homology is an emerging mathematical… read more USED (low confidence) K. N. Lad, “Correlation between atomic-level structure, packing efficiency and glass-forming ability in Cu–Zr metallic glasses,” Journal of Non-crystalline Solids. 2014. link Times cited: 16 USED (low confidence) A. Nakamura, Y. Kamimura, K. Edagawa, and S. Takeuchi, “Elastic and plastic characteristics of a model Cu–Zr amorphous alloy,” Materials Science and Engineering A-structural Materials Properties Microstructure and Processing. 2014. link Times cited: 4 USED (low confidence) M. Li, “Correlation Between Local Atomic Symmetry and Mechanical Properties in Metallic Glasses,” Journal of Materials Science & Technology. 2014. link Times cited: 32 USED (low confidence) C. Wu, N. Karayiannis, M. Laso, D. Qu, Q. Luo, and J. Shen, “A metric to gauge local distortion in metallic glasses and supercooled liquids,” Acta Materialia. 2014. link Times cited: 9 USED (low confidence) F. Li, X. Liu, and Z. Lu, “Atomic structural evolution during glass formation of a Cu–Zr binary metallic glass,” Computational Materials Science. 2014. link Times cited: 56 USED (low confidence) D. Wen, P. Peng, Y.-qi Jiang, Z.-an Tian, R.-su Liu, and K. Dong, “The effect of cooling rates on hereditary characteristics of icosahedral clusters in rapid solidification of liquid Cu56Zr44 alloys,” Journal of Non-crystalline Solids. 2014. link Times cited: 12 USED (low confidence) H. Gleiter, T. Schimmel, and H. Hahn, “Nanostructured solids – From nano-glasses to quantum transistors,” Nano Today. 2014. link Times cited: 108 USED (low confidence) K. Albe, Y. Ritter, and D. Şopu, “Enhancing the plasticity of metallic glasses: Shear band formation, nanocomposites and nanoglasses investigated by molecular dynamics simulations,” Mechanics of Materials. 2013. link Times cited: 163 USED (low confidence) D. Wen, P. Peng, Y.-qi Jiang, and R.-su Liu, “On the heredity and evolution of icosahedral clusters during the rapid solidification of liquid Cu50Zr50 alloys,” Journal of Non-crystalline Solids. 2013. link Times cited: 25 USED (low confidence) R. Soklaski, Z. Nussinov, Z. E. Markow, K. Kelton, and L. Yang, “Connectivity of icosahedral network and a dramatically growing static length scale in Cu-Zr binary metallic glasses,” Physical Review B. 2013. link Times cited: 126 Abstract: We report on and characterize, via molecular dynamics studie… read more USED (low confidence) S. Pan, J. Qin, W. Wang, and T. Gu, “A new method to characterize medium range order in metallic glasses,” Journal of Non-crystalline Solids. 2012. link Times cited: 7 USED (low confidence) D. Miracle, K. Laws, O. Senkov, and G. Wilks, “Partial Coordination Numbers in Binary Metallic Glasses,” Metallurgical and Materials Transactions A. 2012. link Times cited: 16 USED (low confidence) J. Schäfer, Y. Ashkenazy, K. Albe, and R. Averback, “Effect of solute segregation on thermal creep in dilute nanocyrstalline Cu alloys,” Materials Science and Engineering A-structural Materials Properties Microstructure and Processing. 2012. link Times cited: 17 USED (low confidence) A. Lagogianni, D. Papageorgiou, and G. Evangelakis, “Surface properties of the Cu50Zr50 metallic glass decorated with icosahedral CuxZr100−x (0 < x < 100) clusters by molecular dynamics simulations,” Computational Materials Science. 2012. link Times cited: 9 USED (low confidence) Y. Ritter and K. Albe, “Thermal annealing of shear bands in deformed metallic glasses: Recovery mechanisms in Cu64Zr36 studied by molecular dynamics simulations,” Acta Materialia. 2011. link Times cited: 24 USED (low confidence) Y. Ritter, D. Şopu, H. Gleiter, and K. Albe, “Structure, stability and mechanical properties of internal interfaces in Cu64Zr36 nanoglasses studied by MD simulations,” Acta Materialia. 2011. link Times cited: 98 USED (low confidence) J. Harvey, A. Gheribi, and P. Chartrand, “Accurate determination of the Gibbs energy of Cu-Zr melts using the thermodynamic integration method in Monte Carlo simulations.,” The Journal of chemical physics. 2011. link Times cited: 19 Abstract: The design of multicomponent alloys used in different applic… read more USED (low confidence) K. Park, E. Fleury, H. Seok, and Y.-C. Kim, “Deformation behaviors under tension and compression: Atomic simulation of Cu65Zr35 metallic glass,” Intermetallics. 2011. link Times cited: 17 USED (low confidence) K. Park, H. Park, and E. Fleury, “Strain localization in annealed Cu50Zr50 metallic glass,” Materials Science and Engineering A-structural Materials Properties Microstructure and Processing. 2011. link Times cited: 7 USED (low confidence) D. Şopu, Y. Ritter, H. Gleiter, and K. Albe, “Deformation behavior of bulk and nanostructured metallic glasses studied via molecular dynamics simulations,” Physical Review B. 2011. link Times cited: 121 Abstract: In this study, we characterize the mechanical properties of … read more USED (low confidence) C. Valencia-Balvín, C. Loyola, J. Osorio-Guillén, and G. Gutiérrez, “Structural and dynamical properties of the Cu46Zr54 alloy in crystalline, amorphous and liquid state: A molecular dynamicstudy,” Physica B-condensed Matter. 2010. link Times cited: 6 USED (low confidence) B. Arman, S. Luo, T. Germann, and T. Çagin, “Dynamic response of Cu 46 Zr 54 metallic glass to high-strain-rate shock loading: Plasticity, spall, and atomic-level structures,” Physical Review B. 2010. link Times cited: 75 Abstract: We investigate dynamic response of Cu{sub 46}Zr{sub 54} meta… read more USED (low confidence) M. Li, C. Wang, S. Hao, M. Kramer, and K. Ho, “Structural heterogeneity and medium-range order in Zrsub xCusub 100-x metallic glasses,” Physical Review B. 2009. link Times cited: 189 Abstract: Realistic three-dimensional atomistic structures of Zr{sub x… read more USED (low confidence) Q. Cheng, H. Wu, Y. Wang, and X. X. Wang, “Pseudoelasticity of Cu–Zr nanowires via stress-induced martensitic phase transformations,” Applied Physics Letters. 2009. link Times cited: 37 Abstract: Atomistic simulations were performed to investigate the pseu… read more USED (low confidence) Y. Cheng, A. Cao, and E. Ma, “Correlation between the elastic modulus and the intrinsic plastic behavior of metallic glasses: The roles of atomic configuration and alloy composition,” Acta Materialia. 2009. link Times cited: 298 USED (low confidence) D. Zhao, B. Zhu, S. Wang, Y.-T. Niu, L. Xu, and H. Zhao, “Effects of pre-strain on the nanoindentation behaviors of metallic glass studied by molecular dynamics simulations,” Computational Materials Science. 2021. link Times cited: 15 USED (low confidence) W. Zhao, C. Jialin, and G. Li, “Quantitative analysis of structure evolution of Zr-Cu amorphous alloys caused by cooling rates based on atomic bond proportion,” Computational Materials Science. 2021. link Times cited: 3 USED (low confidence) A. Chauhan and M. Shukla, “Molecular dynamics simulation of the effect of temperature and size on the mechanical behavior of Cu50Zr50 metallic glass,” Materials Today: Proceedings. 2021. link Times cited: 1 USED (low confidence) Y. Deng, K. Jiao, and J. Zhang, “Liquid structure evolution of molten iron in blast furnace hearth,” Metallurgical Research & Technology. 2019. link Times cited: 3 Abstract: The iron-carbon interfacial reaction between molten iron and… read more USED (low confidence) С. Волегов, Р. М. Герасимов, and Р. П. Давлятшин, “MODELS OF MOLECULAR DYNAMICS: A REVIEW OF EAM-POTENTIALS. PART 2. POTENTIALS FOR MULTI-COMPONENT SYSTEMS.” 2018. link Times cited: 1 Abstract: Получена: 18 мая 2018 г. Принята: 25 июня 2018 г. Опубликова… read more USED (low confidence) F. Li, H. Zhang, X. Liu, C.-Y. Yu, and Z. Lu, “Effects of cooling rate on the atomic structure of Cu64Zr36 binary metallic glass,” Computational Materials Science. 2018. link Times cited: 25 USED (low confidence) A. Dutta, “Surface damage of CuZr metallic glass by hypervelocity nano-projectile: A molecular dynamics study,” Computational Materials Science. 2018. link Times cited: 6 USED (low confidence) N. Yedla and S. Ghosh, “Nature of atomic trajectories and convective flow during plastic deformation of amorphous Cu50Zr50 alloy at room temperature-classical molecular dynamics studies,” Intermetallics. 2017. link Times cited: 15 USED (low confidence) A. Kumar, P. Gupta, and N. Yedla, “Nanoindentation studies of Zr50Cu50 metallic glass thin film nanocomposites via molecular dynamics simulations,” Revue De Metallurgie-cahiers D Informations Techniques. 2016. link Times cited: 4 Abstract: We carry out molecular dynamics (MD) simulations of nanoinde… read more USED (low confidence) S. Feng, L. Qi, G. Li, and R. Liu, “Molecular dynamics simulation of structural characterization of elastic and inelastic deformation in ZrCu metallic glasses,” Journal of Nanomaterials. 2014. link Times cited: 8 Abstract: The nanoscopic deformation behaviors in a ZrCu metallic glas… read more USED (low confidence) K. Koshiyama and K. Shintani, “Atomistic study of the mechanical properties of metallic-glass nanowires,” MRS Proceedings. 2011. link Times cited: 0 Abstract: Melt-growth simulations based on the molecular-dynamics meth… read more NOT USED (high confidence) R. Forrest, E. Lazar, S. Goel, and J. J. Bean, “Quantifying the differences in properties between polycrystals containing planar and curved grain boundaries,” Nanofabrication. 2022. link Times cited: 0 Abstract: There are several methods in which grain boundaries can be m… read more NOT USED (high confidence) N. Amigo, P. Cortés, and F. Valencia, “Research on metallic glasses at the atomic scale: a systematic review,” Sn Applied Sciences. 2022. link Times cited: 1 NOT USED (high confidence) N. Amigo, “Effect of the atomic construction and preparation procedure on the deformation behaviour of CuZr metallic glasses,” Molecular Simulation. 2021. link Times cited: 2 Abstract: ABSTRACT The construction of metallic glasses (MGs) at the a… read more NOT USED (high confidence) A.-S. Tran, “Control of plastic deformation in Cu50Ta50 metallic glass by insertion of Cu crystalline cores,” Physica Scripta. 2021. link Times cited: 3 Abstract: The tensile characteristics and deformation mechanisms of Cu… read more NOT USED (high confidence) C. Kunka, A. Shanker, E. Y. Chen, S. Kalidindi, and R. Dingreville, “Decoding defect statistics from diffractograms via machine learning,” npj Computational Materials. 2021. link Times cited: 6 NOT USED (high confidence) A. K. A. Lu, K. Nishio, T. Morishita, K. Ohara, Z. Lu, and A. Hirata, “Frank-Kasper Z16 local structures in Cu-Zr metallic glasses,” Physical Review B. 2020. link Times cited: 1 Abstract: Although previous molecular dynamics studies proposed the ex… read more NOT USED (high confidence) B. Lin, J. Wang, J. Li, and Z. Wang, “A neural-network based framework of developing cross interaction in alloy embedded-atom method potentials: application to Zr–Nb alloy,” Journal of Physics: Condensed Matter. 2020. link Times cited: 2 Abstract: Interaction potentials are critical to molecular dynamics si… read more NOT USED (high confidence) M. Kramer and M. Li, “Changes in short- and medium-range order in metallic liquids during undercooling,” MRS Bulletin. 2020. link Times cited: 12 Abstract: It has been widely speculated that dominant motifs, such as … read more NOT USED (high confidence) M. Sepulveda-Macias, G. Gutiérrez, and F. Lund, “Precursors to plastic failure in a numerical simulation of CuZr metallic glass,” Journal of Physics: Condensed Matter. 2019. link Times cited: 2 Abstract: We deform, in pure shear, a thin sample of Cu50Zr50 metallic… read more NOT USED (high confidence) R. Jana and L. Pastewka, “Correlations of non-affine displacements in metallic glasses through the yield transition,” Journal of Physics: Materials. 2019. link Times cited: 18 Abstract: We study correlations of non-affine displacements during sim… read more NOT USED (high confidence) B. Bhattarai, R. Thapa, and D. A. Drabold, “Ab initio inversion of structure and the lattice dynamics of a metallic glass: the case of Pd40Ni40P20,” Modelling and Simulation in Materials Science and Engineering. 2019. link Times cited: 2 Abstract: In this paper we infer the structure of Pd40Ni40P20 from exp… read more NOT USED (high confidence) J. Yang, Y. Wang, E. Ma, A. Zaccone, L. Dai, and M. Jiang, “Structural Parameter of Orientational Order to Predict the Boson Vibrational Anomaly in Glasses.,” Physical review letters. 2019. link Times cited: 34 Abstract: It has so far remained a major challenge to quantitatively p… read more NOT USED (high confidence) R. Christensen, Z. Li, and H. Gao, “An evaluation of the failure modes transition and the Christensen ductile/brittle failure theory using molecular dynamics,” Proceedings of the Royal Society A. 2018. link Times cited: 16 Abstract: The Christensen ductile/brittle failure theory can be interp… read more NOT USED (high confidence) J. Feng, J. Feng, P. Chen, and M. Li, “Local shear dominance in equation of state of metallic glass under hydrostatic pressure,” Journal of Applied Physics. 2018. link Times cited: 3 Abstract: Amorphous solids are generally believed to best obey the equ… read more NOT USED (high confidence) W.-R. Jian, L. Wang, X. Yao, and S.-N. Luo, “Balancing strength, hardness and ductility of Cu64Zr36 nanoglasses via embedded nanocrystals,” Nanotechnology. 2018. link Times cited: 20 Abstract: Superplasticity can be achieved in nanoglasses but at the ex… read more NOT USED (high confidence) S. Alkan and H. Sehitoglu, “Dislocation core effects on slip response of NiTi- a key to understanding shape memory,” International Journal of Plasticity. 2017. link Times cited: 32 NOT USED (high confidence) K. N. Lad, N. Jakse, and A. Pasturel, “How closely do many-body potentials describe the structure and dynamics of Cu-Zr glass-forming alloy?,” The Journal of chemical physics. 2017. link Times cited: 6 Abstract: Molecular dynamics investigations of the structure and dynam… read more NOT USED (high confidence) G. Ren and H. Sehitoglu, “Interatomic potential for the NiTi alloy and its application,” Computational Materials Science. 2016. link Times cited: 45 NOT USED (high confidence) J. Douglas, B. A. P. Betancourt, X. Tong, and H. Zhang, “Localization model description of diffusion and structural relaxation in glass-forming Cu–Zr alloys,” Journal of Statistical Mechanics: Theory and Experiment. 2016. link Times cited: 56 Abstract: We test the localization model (LM) prediction of a paramete… read more NOT USED (high confidence) X. J. Han, J. G. Li, and H. Schober, “High temperature breakdown of the Stokes-Einstein relation in a computer simulated Cu-Zr melt.,” The Journal of chemical physics. 2016. link Times cited: 29 Abstract: Transport properties and the Stokes-Einstein (SE) relation i… read more NOT USED (high confidence) Y. Zhu, G. Liao, T. Shi, M. Li, Z. Tang, and F. Xiong, “Thermoplastic deformation and structural evolutions in nanoimprinting metallic glasses using molecular dynamics analysis,” Journal of Non-crystalline Solids. 2015. link Times cited: 18 NOT USED (high confidence) J. E. Ludy and T. Rupert, “Amorphous intergranular films act as ultra-efficient point defect sinks during collision cascades,” arXiv: Materials Science. 2015. link Times cited: 24 NOT USED (high confidence) Q. Zhang, Q. Li, and M. Li, “Chemical segregation in metallic glass nanowires.,” The Journal of chemical physics. 2014. link Times cited: 16 Abstract: Nanowires made of metallic glass have been actively pursued … read more NOT USED (high confidence) F. Hussain et al., “Molecular dynamics simulation of mechanical characteristics of CuZr bulk metallic glasses using uni-axial tensile loading technique,” Physica Scripta. 2014. link Times cited: 10 Abstract: In the present study, a three-dimensional molecular dynamics… read more NOT USED (high confidence) H. Gleiter, “Nanoglasses: a new kind of noncrystalline materials,” Beilstein Journal of Nanotechnology. 2013. link Times cited: 99 Abstract: Nanoglasses are a new class of noncrystalline solids. They d… read more NOT USED (high confidence) S.-H. Wu et al., “Fluctuation between icosahedral and body-centered-cube short-range orders in undercooled Zr liquid,” Journal of Applied Physics. 2011. link Times cited: 14 Abstract: Ab initio molecular dynamics simulations are performed to st… read more NOT USED (high confidence) M. Chassagne, M. Legros, and D. Rodney, “Atomic-scale simulation of screw dislocation/coherent twin boundary interaction in Al, Au, Cu and Ni,” Acta Materialia. 2011. link Times cited: 124 NOT USED (high confidence) M. Mendelev et al., “Experimental and computer simulation determination of the structural changes occurring through the liquid–glass transition in Cu–Zr alloys,” Philosophical Magazine. 2010. link Times cited: 44 Abstract: Molecular dynamics (MD) simulations were performed of the st… read more NOT USED (high confidence) M. Mendelev and M. Kramer, “Reliability of methods of computer simulation of structure of amorphous alloys,” Journal of Applied Physics. 2010. link Times cited: 16 Abstract: We took a model created by the molecular dynamics (MD) simul… read more NOT USED (high confidence) J. Hwang, A. M. Clausen, H. Cao, and P. Voyles, “Reverse Monte Carlo structural model for a zirconium-based metallic glass incorporating fluctuation microscopy medium-range order data,” Journal of Materials Research. 2009. link Times cited: 24 Abstract: We used reverse Monte Carlo (RMC) modeling to simulate the a… read more NOT USED (high confidence) M. Mendelev, M. Kramer, R. Ott, D. Sordelet, D. Yagodin, and P. Popel,’ “Development of suitable interatomic potentials for simulation of liquid and amorphous Cu–Zr alloys,” Philosophical Magazine. 2009. link Times cited: 334 Abstract: We present a new semi-empirical potential suitable for molec… read more NOT USED (high confidence) M. Mendelev, M. J. Kramer, R. T. Ott, and D. Sordelet, “Molecular dynamics simulation of diffusion in supercooled Cu–Zr alloys,” Philosophical Magazine. 2009. link Times cited: 60 Abstract: Molecular dynamics (MD) simulations of diffusion in Cu–Zr al… read more NOT USED (high confidence) M. Mendelev, R. Ott, M. Heggen, M. Feuerebacher, M. Kramer, and D. Sordelet, “Deformation behavior of an amorphous Cu64.5Zr35.5 alloy: A combined computer simulation and experimental study,” Journal of Applied Physics. 2008. link Times cited: 21 Abstract: Molecular dynamics (MD) simulations were performed to examin… read more NOT USED (definite) Y. Hu et al., “Atomic scale study of stress-induced misaligned subsurface layers in KDP crystals,” Scientific Reports. 2019. link Times cited: 6 NOT USED (definite) Y. Hu, J. Schuler, and T. Rupert, “Identifying interatomic potentials for the accurate modeling of interfacial segregation and structural transitions,” Computational Materials Science. 2017. link Times cited: 16 NOT USED (definite) S. Liu, S. Liu, F.-gen Li, M. Li, and W.-Q. Wang, “Structural and dynamical characteristics of flow units in metallic glasses,” Scientific Reports. 2017. link Times cited: 8 NOT USED (definite) W. B. Zhang et al., “Size effect on atomic structure in low-dimensional Cu-Zr amorphous systems,” Scientific Reports. 2017. link Times cited: 12 NOT USED (definite) Z. W. Wu, M. Li, W. Wang, and K. Liu, “Hidden topological order and its correlation with glass-forming ability in metallic glasses,” Nature Communications. 2015. link Times cited: 111 NOT USED (definite) D. Rodney, A. Tanguy, and D. Vandembroucq, “Modeling the mechanics of amorphous solids at different length scale and time scale,” Modelling and Simulation in Materials Science and Engineering. 2011. link Times cited: 244 Abstract: We review the recent literature on the simulation of the str… read more |
| Funding | Not available |
| Short KIM ID
The unique KIM identifier code.
| MO_120596890176_005 |
| Extended KIM ID
The long form of the KIM ID including a human readable prefix (100 characters max), two underscores, and the Short KIM ID. Extended KIM IDs can only contain alpha-numeric characters (letters and digits) and underscores and must begin with a letter.
| EAM_Dynamo_MendelevSordeletKramer_2007_CuZr__MO_120596890176_005 |
| DOI |
10.25950/8556dbaf https://doi.org/10.25950/8556dbaf https://commons.datacite.org/doi.org/10.25950/8556dbaf |
| KIM Item Type
Specifies whether this is a Portable Model (software implementation of an interatomic model); Portable Model with parameter file (parameter file to be read in by a Model Driver); Model Driver (software implementation of an interatomic model that reads in parameters).
| Portable Model using Model Driver EAM_Dynamo__MD_120291908751_005 |
| Driver | EAM_Dynamo__MD_120291908751_005 |
| KIM API Version | 2.0 |
| Potential Type | eam |
| Programming Language(s)
The programming languages used in the code and the percentage of the code written in each one. "N/A" means "not applicable" and refers to model parameterizations which only include parameter tables and have no programming language.
| N/A |
| Previous Version | EAM_Dynamo_MendelevSordeletKramer_2007_CuZr__MO_120596890176_004 |
| Grade | Name | Category | Brief Description | Full Results | Aux File(s) |
|---|---|---|---|---|---|
| P | vc-species-supported-as-stated | mandatory | The model supports all species it claims to support; see full description. |
Results | Files |
| P | vc-periodicity-support | mandatory | Periodic boundary conditions are handled correctly; see full description. |
Results | Files |
| P | vc-permutation-symmetry | mandatory | Total energy and forces are unchanged when swapping atoms of the same species; see full description. |
Results | Files |
| B | vc-forces-numerical-derivative | consistency | Forces computed by the model agree with numerical derivatives of the energy; see full description. |
Results | Files |
| P | vc-dimer-continuity-c1 | informational | The energy versus separation relation of a pair of atoms is C1 continuous (i.e. the function and its first derivative are continuous); see full description. |
Results | Files |
| P | vc-objectivity | informational | Total energy is unchanged and forces transform correctly under rigid-body translation and rotation; see full description. |
Results | Files |
| P | vc-inversion-symmetry | informational | Total energy is unchanged and forces change sign when inverting a configuration through the origin; see full description. |
Results | Files |
| N/A | vc-memory-leak | informational | The model code does not have memory leaks (i.e. it releases all allocated memory at the end); see full description. |
Results | Files |
| P | vc-thread-safe | mandatory | The model returns the same energy and forces when computed in serial and when using parallel threads for a set of configurations. Note that this is not a guarantee of thread safety; see full description. |
Results | Files |
| P | vc-unit-conversion | mandatory | The model is able to correctly convert its energy and/or forces to different unit sets; see full description. |
Results | Files |
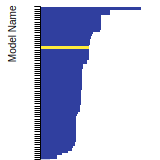
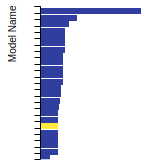
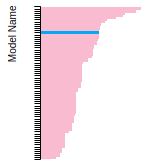
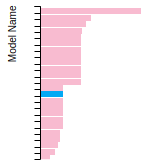
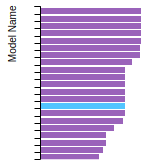
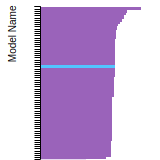
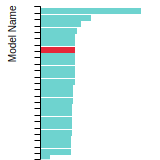
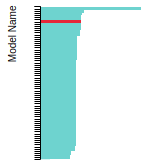
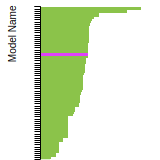
BCC Lattice Constant
This bar chart plot shows the mono-atomic body-centered cubic (bcc) lattice constant predicted by the current model (shown in the unique color) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
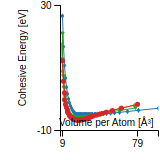
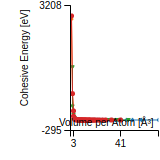
Cohesive Energy Graph
This graph shows the cohesive energy versus volume-per-atom for the current mode for four mono-atomic cubic phases (body-centered cubic (bcc), face-centered cubic (fcc), simple cubic (sc), and diamond). The curve with the lowest minimum is the ground state of the crystal if stable. (The crystal structure is enforced in these calculations, so the phase may not be stable.) Graphs are generated for each species supported by the model.
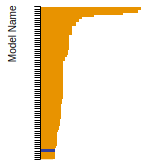
Diamond Lattice Constant
This bar chart plot shows the mono-atomic face-centered diamond lattice constant predicted by the current model (shown in the unique color) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
Dislocation Core Energies
This graph shows the dislocation core energy of a cubic crystal at zero temperature and pressure for a specific set of dislocation core cutoff radii. After obtaining the total energy of the system from conjugate gradient minimizations, non-singular, isotropic and anisotropic elasticity are applied to obtain the dislocation core energy for each of these supercells with different dipole distances. Graphs are generated for each species supported by the model.
(No matching species)FCC Elastic Constants
This bar chart plot shows the mono-atomic face-centered cubic (fcc) elastic constants predicted by the current model (shown in blue) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
FCC Lattice Constant
This bar chart plot shows the mono-atomic face-centered cubic (fcc) lattice constant predicted by the current model (shown in red) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
FCC Stacking Fault Energies
This bar chart plot shows the intrinsic and extrinsic stacking fault energies as well as the unstable stacking and unstable twinning energies for face-centered cubic (fcc) predicted by the current model (shown in blue) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
FCC Surface Energies
This bar chart plot shows the mono-atomic face-centered cubic (fcc) relaxed surface energies predicted by the current model (shown in blue) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
SC Lattice Constant
This bar chart plot shows the mono-atomic simple cubic (sc) lattice constant predicted by the current model (shown in the unique color) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
Cubic Crystal Basic Properties Table
Species: CuSpecies: Zr
Disclaimer From Model Developer
The authors note in the paper that this potential was never intended for serious simulation. An improved Cu-Zr model can be found in KIM item https://openkim.org/id/MO_609260676108_000.
Creators:
Contributor: karls
Publication Year: 2019
DOI: https://doi.org/10.25950/64cb38c5
This Test Driver uses LAMMPS to compute the cohesive energy of a given monoatomic cubic lattice (fcc, bcc, sc, or diamond) at a variety of lattice spacings. The lattice spacings range from a_min (=a_min_frac*a_0) to a_max (=a_max_frac*a_0) where a_0, a_min_frac, and a_max_frac are read from stdin (a_0 is typically approximately equal to the equilibrium lattice constant). The precise scaling and number of lattice spacings sampled between a_min and a_0 (a_0 and a_max) is specified by two additional parameters passed from stdin: N_lower and samplespacing_lower (N_upper and samplespacing_upper). Please see README.txt for further details.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Cohesive energy versus lattice constant curve for bcc Cu v004 | view | 14829 | |
| Cohesive energy versus lattice constant curve for bcc Zr v004 | view | 12283 | |
| Cohesive energy versus lattice constant curve for diamond Cu v004 | view | 21208 | |
| Cohesive energy versus lattice constant curve for diamond Zr v004 | view | 12999 | |
| Cohesive energy versus lattice constant curve for fcc Cu v004 | view | 13835 | |
| Cohesive energy versus lattice constant curve for fcc Zr v004 | view | 12482 | |
| Cohesive energy versus lattice constant curve for sc Cu v004 | view | 19456 | |
| Cohesive energy versus lattice constant curve for sc Zr v004 | view | 13865 |
Creators:
Contributor: ilia
Publication Year: 2024
DOI: https://doi.org/10.25950/888f9943
Computes the elastic constants for an arbitrary crystal. A robust computational protocol is used, attempting multiple methods and step sizes to achieve an acceptably low error in numerical differentiation and deviation from material symmetry. The crystal structure is specified using the AFLOW prototype designation as part of the Crystal Genome testing framework. In addition, the distance from the obtained elasticity tensor to the nearest isotropic tensor is computed.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Elastic constants for CuZr in AFLOW crystal prototype A10B7_oC68_64_f2g_adef at zero temperature and pressure v000 | view | 259871 |
Creators: Junhao Li and Ellad Tadmor
Contributor: tadmor
Publication Year: 2019
DOI: https://doi.org/10.25950/5853fb8f
Computes the cubic elastic constants for some common crystal types (fcc, bcc, sc, diamond) by calculating the hessian of the energy density with respect to strain. An estimate of the error associated with the numerical differentiation performed is reported.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Elastic constants for bcc Cu at zero temperature v006 | view | 2047 | |
| Elastic constants for bcc Zr at zero temperature v006 | view | 6398 | |
| Elastic constants for diamond Cu at zero temperature v001 | view | 6366 | |
| Elastic constants for diamond Zr at zero temperature v001 | view | 11580 | |
| Elastic constants for fcc Cu at zero temperature v006 | view | 2367 | |
| Elastic constants for fcc Zr at zero temperature v006 | view | 2015 | |
| Elastic constants for sc Cu at zero temperature v006 | view | 1887 | |
| Elastic constants for sc Zr at zero temperature v006 | view | 6526 |
Creators: Junhao Li
Contributor: jl2922
Publication Year: 2019
DOI: https://doi.org/10.25950/d794c746
Computes the elastic constants for hcp crystals by calculating the hessian of the energy density with respect to strain. An estimate of the error associated with the numerical differentiation performed is reported.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Elastic constants for hcp Cu at zero temperature v004 | view | 2260 | |
| Elastic constants for hcp Zr at zero temperature v004 | view | 1942 |
Creators:
Contributor: ilia
Publication Year: 2023
DOI: https://doi.org/10.25950/e8a7ed84
Computes the equilibrium crystal structure and energy for an arbitrary crystal at zero temperature and applied stress by performing symmetry-constrained relaxation. The crystal structure is specified using the AFLOW prototype designation. Multiple sets of free parameters corresponding to the crystal prototype may be specified as initial guesses for structure optimization. No guarantee is made regarding the stability of computed equilibria, nor that any are the ground state.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Equilibrium crystal structure and energy for Cu in AFLOW crystal prototype A_cF4_225_a v001 | view | 83265 | |
| Equilibrium crystal structure and energy for Cu in AFLOW crystal prototype A_cI2_229_a v001 | view | 73547 |
Creators:
Contributor: ilia
Publication Year: 2024
DOI: https://doi.org/10.25950/2f2c4ad3
Computes the equilibrium crystal structure and energy for an arbitrary crystal at zero temperature and applied stress by performing symmetry-constrained relaxation. The crystal structure is specified using the AFLOW prototype designation. Multiple sets of free parameters corresponding to the crystal prototype may be specified as initial guesses for structure optimization. No guarantee is made regarding the stability of computed equilibria, nor that any are the ground state.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Equilibrium crystal structure and energy for CuZr in AFLOW crystal prototype A5B_cF24_216_ae_c v002 | view | 152983 | |
| Equilibrium crystal structure and energy for CuZr in AFLOW crystal prototype AB2_cF96_227_e_cf v002 | view | 769629 | |
| Equilibrium crystal structure and energy for CuZr in AFLOW crystal prototype AB2_tI6_139_a_e v002 | view | 44294 | |
| Equilibrium crystal structure and energy for CuZr in AFLOW crystal prototype AB_cP2_221_a_b v002 | view | 88786 | |
| Equilibrium crystal structure and energy for CuZr in AFLOW crystal prototype AB_mC16_8_2ab_2ab v002 | view | 85621 | |
| Equilibrium crystal structure and energy for CuZr in AFLOW crystal prototype AB_oC8_63_c_c v002 | view | 45084 |
Creators:
Contributor: ilia
Publication Year: 2025
DOI: https://doi.org/10.25950/866c7cfa
Computes the equilibrium crystal structure and energy for an arbitrary crystal at zero temperature and applied stress by performing symmetry-constrained relaxation. The crystal structure is specified using the AFLOW prototype designation. Multiple sets of free parameters corresponding to the crystal prototype may be specified as initial guesses for structure optimization. No guarantee is made regarding the stability of computed equilibria, nor that any are the ground state.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Equilibrium crystal structure and energy for CuZr in AFLOW crystal prototype A10B7_oC68_64_f2g_adef v003 | view | 593240 | |
| Equilibrium crystal structure and energy for Zr in AFLOW crystal prototype A_cF4_225_a v003 | view | 143151 | |
| Equilibrium crystal structure and energy for Zr in AFLOW crystal prototype A_cI2_229_a v003 | view | 135981 | |
| Equilibrium crystal structure and energy for Zr in AFLOW crystal prototype A_hP2_194_c v003 | view | 139870 |
Creators:
Contributor: brunnels
Publication Year: 2022
DOI: https://doi.org/10.25950/2c59c9d6
Computes grain boundary energy for a range of tilt angles given a crystal structure, tilt axis, and material.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Relaxed energy as a function of tilt angle for a 100 symmetric tilt grain boundary in fcc Cu v001 | view | 10375379 | |
| Relaxed energy as a function of tilt angle for a 110 symmetric tilt grain boundary in fcc Cu v001 | view | 56557017 | |
| Relaxed energy as a function of tilt angle for a 111 symmetric tilt grain boundary in fcc Cu v001 | view | 30189425 | |
| Relaxed energy as a function of tilt angle for a 112 symmetric tilt grain boundary in fcc Cu v001 | view | 108698943 |
Creators: Daniel S. Karls and Junhao Li
Contributor: karls
Publication Year: 2019
DOI: https://doi.org/10.25950/2765e3bf
Equilibrium lattice constant and cohesive energy of a cubic lattice at zero temperature and pressure.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Equilibrium zero-temperature lattice constant for bcc Cu v007 | view | 2495 | |
| Equilibrium zero-temperature lattice constant for bcc Zr v007 | view | 2399 | |
| Equilibrium zero-temperature lattice constant for diamond Cu v007 | view | 3263 | |
| Equilibrium zero-temperature lattice constant for diamond Zr v007 | view | 4606 | |
| Equilibrium zero-temperature lattice constant for fcc Cu v007 | view | 4223 | |
| Equilibrium zero-temperature lattice constant for fcc Zr v007 | view | 2751 | |
| Equilibrium zero-temperature lattice constant for sc Cu v007 | view | 2335 | |
| Equilibrium zero-temperature lattice constant for sc Zr v007 | view | 2335 |
Creators: Daniel S. Karls and Junhao Li
Contributor: karls
Publication Year: 2019
DOI: https://doi.org/10.25950/c339ca32
Calculates lattice constant of hexagonal bulk structures at zero temperature and pressure by using simplex minimization to minimize the potential energy.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Equilibrium lattice constants for hcp Cu v005 | view | 53389 | |
| Equilibrium lattice constants for hcp Zr v005 | view | 23177 |
Creators: Mingjian Wen
Contributor: mjwen
Publication Year: 2019
DOI: https://doi.org/10.25950/fc69d82d
This Test Driver uses LAMMPS to compute the linear thermal expansion coefficient at a finite temperature under a given pressure for a cubic lattice (fcc, bcc, sc, diamond) of a single given species.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Linear thermal expansion coefficient of fcc Cu at 293.15 K under a pressure of 0 MPa v001 | view | 13562216 |
Creators: Matt Bierbaum
Contributor: mattbierbaum
Publication Year: 2019
DOI: https://doi.org/10.25950/64f4999b
Calculates the phonon dispersion relations for fcc lattices and records the results as curves.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Phonon dispersion relations for fcc Cu v004 | view | 52846 |
Creators:
Contributor: SubrahmanyamPattamatta
Publication Year: 2019
DOI: https://doi.org/10.25950/b4cfaf9a
Intrinsic and extrinsic stacking fault energies, unstable stacking fault energy, unstable twinning energy, stacking fault energy as a function of fractional displacement, and gamma surface for a monoatomic FCC lattice at zero temperature and pressure.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Stacking and twinning fault energies for fcc Cu v002 | view | 13553803 |
Creators: Matt Bierbaum
Contributor: mattbierbaum
Publication Year: 2019
DOI: https://doi.org/10.25950/6c43a4e6
Calculates the surface energy of several high symmetry surfaces and produces a broken-bond model fit. In latex form, the fit equations are given by:
E_{FCC} (\vec{n}) = p_1 (4 \left( |x+y| + |x-y| + |x+z| + |x-z| + |z+y| +|z-y|\right)) + p_2 (8 \left( |x| + |y| + |z|\right)) + p_3 (2 ( |x+ 2y + z| + |x+2y-z| + |x-2y + z| + |x-2y-z| + |2x+y+z| + |2x+y-z| +|2x-y+z| +|2x-y-z| +|x+y+2z| +|x+y-2z| +|x-y+2z| +|x-y-2z| ) + c
E_{BCC} (\vec{n}) = p_1 (6 \left( | x+y+z| + |x+y-z| + |-x+y-z| + |x-y+z| \right)) + p_2 (8 \left( |x| + |y| + |z|\right)) + p_3 (4 \left( |x+y| + |x-y| + |x+z| + |x-z| + |z+y| +|z-y|\right)) +c.
In Python, these two fits take the following form:
def BrokenBondFCC(params, index):
import numpy
x, y, z = index
x = x / numpy.sqrt(x**2.+y**2.+z**2.)
y = y / numpy.sqrt(x**2.+y**2.+z**2.)
z = z / numpy.sqrt(x**2.+y**2.+z**2.)
return params[0]*4* (abs(x+y) + abs(x-y) + abs(x+z) + abs(x-z) + abs(z+y) + abs(z-y)) + params[1]*8*(abs(x) + abs(y) + abs(z)) + params[2]*(abs(x+2*y+z) + abs(x+2*y-z) +abs(x-2*y+z) +abs(x-2*y-z) + abs(2*x+y+z) +abs(2*x+y-z) +abs(2*x-y+z) +abs(2*x-y-z) + abs(x+y+2*z) +abs(x+y-2*z) +abs(x-y+2*z) +abs(x-y-2*z))+params[3]
def BrokenBondBCC(params, x, y, z):
import numpy
x, y, z = index
x = x / numpy.sqrt(x**2.+y**2.+z**2.)
y = y / numpy.sqrt(x**2.+y**2.+z**2.)
z = z / numpy.sqrt(x**2.+y**2.+z**2.)
return params[0]*6*(abs(x+y+z) + abs(x-y-z) + abs(x-y+z) + abs(x+y-z)) + params[1]*8*(abs(x) + abs(y) + abs(z)) + params[2]*4* (abs(x+y) + abs(x-y) + abs(x+z) + abs(x-z) + abs(z+y) + abs(z-y)) + params[3]
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Broken-bond fit of high-symmetry surface energies in fcc Cu v004 | view | 39538 |
Creators:
Contributor: efuem
Publication Year: 2023
DOI: https://doi.org/10.25950/fca89cea
Computes the monovacancy formation energy and relaxation volume for cubic and hcp monoatomic crystals.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Monovacancy formation energy and relaxation volume for fcc Cu | view | 700057 | |
| Monovacancy formation energy and relaxation volume for hcp Zr | view | 402115 |
Creators:
Contributor: efuem
Publication Year: 2023
DOI: https://doi.org/10.25950/c27ba3cd
Computes the monovacancy formation and migration energies for cubic and hcp monoatomic crystals.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Vacancy formation and migration energy for fcc Cu | view | 2799714 | |
| Vacancy formation and migration energy for hcp Zr | view | 2681406 |
| Test | Error Categories | Link to Error page |
|---|---|---|
| Elastic constants for CuZr in AFLOW crystal prototype A10B7_oC68_64_f2g_adef at zero temperature and pressure v000 | other | view |
EquilibriumCrystalStructure__TD_457028483760_002
| Test | Error Categories | Link to Error page |
|---|---|---|
| Equilibrium crystal structure and energy for CuZr in AFLOW crystal prototype AB3_tP4_123_a_ce v002 | other | view |
| Equilibrium crystal structure and energy for CuZr in AFLOW crystal prototype AB_mP4_11_e_e v002 | other | view |
LatticeConstantCubicEnergy__TD_475411767977_006
| Test | Error Categories | Link to Error page |
|---|---|---|
| Equilibrium zero-temperature lattice constant for bcc Zr | other | view |
LatticeConstantHexagonalEnergy__TD_942334626465_004
| Test | Error Categories | Link to Error page |
|---|---|---|
| Equilibrium lattice constants for hcp Zr | other | view |
No Driver
| Verification Check | Error Categories | Link to Error page |
|---|---|---|
| DimerContinuityC1__VC_303890932454_005 | other | view |
| EAM_Dynamo_MendelevSordeletKramer_2007_CuZr__MO_120596890176_005.txz | Tar+XZ | Linux and OS X archive |
| EAM_Dynamo_MendelevSordeletKramer_2007_CuZr__MO_120596890176_005.zip | Zip | Windows archive |
This Model requires a Model Driver. Archives for the Model Driver EAM_Dynamo__MD_120291908751_005 appear below.
| EAM_Dynamo__MD_120291908751_005.txz | Tar+XZ | Linux and OS X archive |
| EAM_Dynamo__MD_120291908751_005.zip | Zip | Windows archive |