EAM_Dynamo_OnatDurukanoglu_2014_CuNi__MO_592013496703_005
EAM_Dynamo_OnatDurukanoglu_2014_CuNi__MO_592013496703_005
| Title
A single sentence description.
|
EAM potential (LAMMPS cubic hermite tabulation) for Cu-Ni alloys developed by Onat and Durukanoğlu (2014) v005 |
|---|---|
| Description
A short description of the Model describing its key features including for example: type of model (pair potential, 3-body potential, EAM, etc.), modeled species (Ac, Ag, ..., Zr), intended purpose, origin, and so on.
|
An optimized EAM potential for Cu-Ni alloys. The potential is determined by fitting to experimental and first-principles data for Cu, Ni and Cu-Ni binary compounds, such as lattice constants, cohesive energies, bulk modulus, elastic constants, diatomic bond lengths and bond energies. The generated potentials were tested by computing a variety of properties of pure elements and the alloy of Cu, Ni: the melting points, alloy mixing enthalpy, lattice specific heat, equilibrium lattice structures, vacancy formation and interstitial formation energies, and various diffusion barriers on the (100) and (111) surfaces of Cu and Ni. The details of the fitting procedure and the predictions of the potential are published at http://dx.doi.org/10.1088/0953-8984/26/3/035404. Using the developed potential, the vibrational thermodynamic functions of Cu-Ni alloys are also investigated and the results are published at http://epjb.epj.org/articles/epjb/abs/2014/11/b140315/b140315.html. This model uses parameter file 'CuNi_v2.eam.alloy', which is a newer version of the parameter file 'CuNi.eam.alloy' distributed with the LAMMPS simulation package. |
| Species
The supported atomic species.
| Cu, Ni |
| Disclaimer
A statement of applicability provided by the contributor, informing users of the intended use of this KIM Item.
|
This potential is tabulated using more spline points to provide smoother cutoff and better accuracy for simulations. |
| Contributor |
Berk Onat |
| Maintainer |
Berk Onat |
| Developer |
Yuri Mishin Papaconstantopoulos, D. A. Mehl, M. J. |
| Published on KIM | 2018 |
| How to Cite | Click here to download this citation in BibTeX format. |
| Citations
This panel presents information regarding the papers that have cited the interatomic potential (IP) whose page you are on. The OpenKIM machine learning based Deep Citation framework is used to determine whether the citing article actually used the IP in computations (denoted by "USED") or only provides it as a background citation (denoted by "NOT USED"). For more details on Deep Citation and how to work with this panel, click the documentation link at the top of the panel. The word cloud to the right is generated from the abstracts of IP principle source(s) (given below in "How to Cite") and the citing articles that were determined to have used the IP in order to provide users with a quick sense of the types of physical phenomena to which this IP is applied. The bar chart shows the number of articles that cited the IP per year. Each bar is divided into green (articles that USED the IP) and blue (articles that did NOT USE the IP). Users are encouraged to correct Deep Citation errors in determination by clicking the speech icon next to a citing article and providing updated information. This will be integrated into the next Deep Citation learning cycle, which occurs on a regular basis. OpenKIM acknowledges the support of the Allen Institute for AI through the Semantic Scholar project for providing citation information and full text of articles when available, which are used to train the Deep Citation ML algorithm. |
This panel provides information on past usage of this interatomic potential (IP) powered by the OpenKIM Deep Citation framework. The word cloud indicates typical applications of the potential. The bar chart shows citations per year of this IP (bars are divided into articles that used the IP (green) and those that did not (blue)). The complete list of articles that cited this IP is provided below along with the Deep Citation determination on usage. See the Deep Citation documentation for more information. 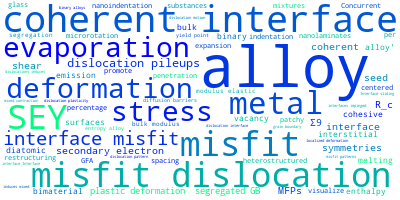
80 Citations (63 used)
Help us to determine which of the papers that cite this potential actually used it to perform calculations. If you know, click the .
USED (high confidence) B. Waters, D. S. Karls, I. Nikiforov, R. Elliott, E. Tadmor, and B. Runnels, “Automated determination of grain boundary energy and potential-dependence using the OpenKIM framework,” Computational Materials Science. 2022. link Times cited: 5 USED (high confidence) J. Qi, C. Oberdorfer, W. Windl, and E. Marquis, “Ab initio
simulation of field evaporation,” Physical Review Materials. 2022. link Times cited: 5 Abstract: A new simulation approach of field evaporation is presented.… read more USED (high confidence) X. Chen, “Effect of phase interface atomic coherency on dynamics of dislocations,” Journal of Materials Research. 2021. link Times cited: 0 Abstract: Coarse-grained atomistic simulations are conducted to study … read more USED (high confidence) R. Gutierrez, I. Matanovic, M. Polak, R. Johnson, D. Morgan, and E. Schamiloglu, “First principles inelastic mean free paths coupled with Monte Carlo simulation of secondary electron yield of Cu-Ni, Cu-Zn, and Mo-Li,” Journal of Applied Physics. 2021. link Times cited: 6 Abstract: Secondary electron yield (SEY) is relevant for widely used c… read more USED (high confidence) A. Selimov, S. Xu, Y. Chen, and D. McDowell, “Lattice dislocation induced misfit dislocation evolution in semi-coherent 111 bimetal interfaces,” Journal of Materials Research. 2021. link Times cited: 5 Abstract: The study of dislocation plasticity mediated by semi-coheren… read more USED (high confidence) M. Wagih, P. M. Larsen, and C. Schuh, “Learning grain boundary segregation energy spectra in polycrystals,” Nature Communications. 2020. link Times cited: 62 USED (high confidence) Z. Mao et al., “The Obstruction Effect of Ni Layer on the Interdiffusion of Cu Substrate and Sn Solder: A Theoretical Investigation,” Journal of Electronic Materials. 2020. link Times cited: 6 USED (high confidence) M. M. Rahman, M. Islam, and N. Anjum, “Investigation on mechanical behaviors of Cu-Ni binary alloy nanopillars: a molecular dynamics study,” Journal of Molecular Modeling. 2020. link Times cited: 3 USED (high confidence) Y.-C. Hu, K. Zhang, S. A. Kube, J. Schroers, M. Shattuck, and C. O’Hern, “Glass formation in binary alloys with different atomic symmetries,” arXiv: Materials Science. 2020. link Times cited: 4 Abstract: Prediction of the glass forming ability (GFA) of alloys rema… read more USED (high confidence) S. Mahmoud and N. Mousseau, “Long-time point defect diffusion in ordered nickel-based binary alloys: How small kinetic differences can lead to completely long-time structural evolution,” Materialia. 2018. link Times cited: 15 USED (high confidence) E. Ilker, M. Madran, M. Konuk, and S. Durukanoğlu, “Growth and shape stability of Cu-Ni core-shell nanoparticles: an atomistic perspective.,” Chemical communications. 2018. link Times cited: 5 Abstract: The growth and shape stability of bi-metallic cubic Cu-Ni na… read more USED (high confidence) W. Nöhring and W. Curtin, “Cross-slip of long dislocations in FCC solid solutions,” Acta Materialia. 2018. link Times cited: 37 USED (high confidence) C. Wu, T. Fang, Y.-J. Lin, and Y.-D. Jie, “Nanowelding of nickel and copper investigated using quasi-continuum simulations,” Multiscale and Multidisciplinary Modeling, Experiments and Design. 2018. link Times cited: 1 USED (high confidence) X. Liu, H. Zhang, and X. Cheng, “Effect of nickel segregation on CuΣ9 grain boundary undergone shear deformations,” Chinese Physics B. 2018. link Times cited: 3 Abstract: Impurity segregation at grain boundary (GB) can significantl… read more USED (low confidence) T. Swinburne, “Coarse-Graining and Forecasting Atomic Material Simulations with Descriptors,” Physical Review Letters. 2023. link Times cited: 0 USED (low confidence) E. Ilker, M. Konuk, M. Madran, M. Gökçen, İ. Göksal, and S. Durukanoğlu, “The role of atomistic processes in growth of Cu–Ni metallic/bimetallic nanoparticles,” Computational Materials Science. 2023. link Times cited: 0 USED (low confidence) A. Kartamyshev, A. Lipnitskii, V. Maksimenko, A. V. Vyazmin, I. Nelasov, and D. Poletaev, “N-body potential for simulating lattice defects and diffusion in copper,” Computational Materials Science. 2023. link Times cited: 1 USED (low confidence) Y.-chun Liu, Y.-chao Liang, L.-li Zhou, T. Gao, Q. Chen, and Z. Tian, “Strengthening mechanism of Ni–Cu nanotwins with void under different tensile directions based on Molecular Dynamics simulation,” Physica B: Condensed Matter. 2023. link Times cited: 0 USED (low confidence) B. Yao, Z. R. Liu, D. Legut, and R. F. Zhang, “Hybrid potential model with high feasibility and flexibility for metallic and covalent solids,” Physical Review B. 2023. link Times cited: 0 USED (low confidence) Z. Zhang and C. Deng, “Solid solution softening in single crystalline metal nanowires studied by atomistic simulations,” Physical Review Materials. 2023. link Times cited: 0 USED (low confidence) S. Dong, X.-Y. Liu, Y. Chen, and C. Zhou, “Atomistic analysis of plastic deformation and shear band formation in FCC/FCC metallic nanolayered composites,” Journal of Materials Research. 2023. link Times cited: 1 Abstract: Atomistic simulations were used to explore the plastic defor… read more USED (low confidence) M. Jain et al., “Strengthening of 3D printed Cu micropillar in Cu-Ni core-shell structure,” Materials & Design. 2023. link Times cited: 2 USED (low confidence) Y. Tian, F. Chen, Z. Cui, and X. Tian, “Effects of atomic size misfit on dislocation mobility in FCC dense solid solution: Atomic simulations and phenomenological modeling,” International Journal of Plasticity. 2022. link Times cited: 4 USED (low confidence) A. Abu-Odeh, T. Allaparti, and M. Asta, “Structure and glide of Lomer and Lomer-Cottrell dislocations: Atomistic simulations for model concentrated alloy solid solutions,” Physical Review Materials. 2022. link Times cited: 0 USED (low confidence) S. Lian, J. Wang, H. Swart, and J. J. Terblans, “Molecular dynamics simulation and thermodynamics calculation on surface segregation in Ni-Cu nano-films under stress,” Physica Scripta. 2022. link Times cited: 0 Abstract: The surface segregation of Cu atoms in a Ni-Cu system was in… read more USED (low confidence) T.-N. Vu, V.-T. Pham, and T. Fang, “Deformation mechanisms and mechanical properties of nanocrystalline CuxNi100-x alloys during indentation using molecular dynamics,” Materials Today Communications. 2022. link Times cited: 9 USED (low confidence) A. Selimov, K. Chu, and D. McDowell, “Effects of interdiffusion on shear response of semi-coherent 111 interfaces in Ni/Cu,” International Journal of Plasticity. 2022. link Times cited: 3 USED (low confidence) M. Settem, P. Kumar, I. Adlakha, and A. Kanjarla, “Surface reconstruction in core@shell nanoalloys: interplay between size and strain,” Acta Materialia. 2022. link Times cited: 3 USED (low confidence) Y. Wang, K. Niu, L. Wang, and W. Xia, “A molecular dynamics study of mechanical properties of bioinspired functionally graded Cu-Ni alloy,” Molecular Simulation. 2022. link Times cited: 2 Abstract: ABSTRACT Inspired from natural materials, functionally grade… read more USED (low confidence) C. Kondur and K. Stephani, “A semi-classical phonon-induced desorption model for carbon surfaces,” AIAA SCITECH 2022 Forum. 2022. link Times cited: 0 USED (low confidence) I. Bryukhanov and V. Emelyanov, “Shear stress relaxation through the motion of edge dislocations in Cu and Cu–Ni solid solution: A molecular dynamics and discrete dislocation study,” Computational Materials Science. 2022. link Times cited: 8 USED (low confidence) S. Wei et al., “Molecular dynamics simulation of compression induced phase transformation in Cu1Ni3 alloy,” Ferroelectrics. 2021. link Times cited: 0 Abstract: The phase transformation mechanism and transformation path o… read more USED (low confidence) X. Shen, B. Yao, Z. R. Liu, D. Legut, H. J. Zhang, and R. Zhang, “Mechanistic insights into interface-facilitated dislocation nucleation and phase transformation at semicoherent bimetal interfaces,” International Journal of Plasticity. 2021. link Times cited: 11 USED (low confidence) B. Yao, Z. Liu, and R. Zhang, “EAPOTs: An integrated empirical interatomic potential optimization platform for single elemental solids,” Computational Materials Science. 2021. link Times cited: 3 USED (low confidence) B. Yao et al., “Cooperative roles of stacking fault energies on dislocation nucleation at bimetal interface through tunable potentials,” Computational Materials Science. 2021. link Times cited: 5 USED (low confidence) M. Rahman, E. Chowdhury, and S. Hong, “Nature of creep deformation in nanocrystalline cupronickel alloy: A Molecular Dynamics study.” 2021. link Times cited: 10 USED (low confidence) A. Galashev, K. Ivanichkina, A. Vorob’ev, O. Rakhmanova, K. Katin, and M. Maslov, “Improved lithium-ion batteries and their communication with hydrogen power,” International Journal of Hydrogen Energy. 2021. link Times cited: 9 USED (low confidence) I. Bryukhanov, “Dynamics of edge dislocation in Cu–Ni solid solution alloys at atomic scale,” International Journal of Plasticity. 2020. link Times cited: 25 USED (low confidence) J. Li, H.-W. Chen, Q. Fang, C. Jiang, Y. Liu, and P. Liaw, “Unraveling the dislocation–precipitate interactions in high-entropy alloys,” International Journal of Plasticity. 2020. link Times cited: 68 USED (low confidence) N. Kaur, C. Deng, and O. Ojo, “Effect of solute segregation on diffusion induced grain boundary migration studied by molecular dynamics simulations,” Computational Materials Science. 2020. link Times cited: 12 USED (low confidence) Z. R. Liu et al., “Mechanistic understanding of the size effect on shock facilitated dislocation nucleation at semicoherent interfaces,” Scripta Materialia. 2020. link Times cited: 9 USED (low confidence) A.-V. Pham, T. Fang, A.-S. Tran, and T.-H. Chen, “Effect of annealing and deposition of Cu atoms on Ni trench to interface formation and growth mechanisms of Cu coating,” Superlattices and Microstructures. 2020. link Times cited: 8 USED (low confidence) Y. Yang et al., “Cooperative Atom Motion in Ni–Cu Nanoparticles during the Structural Evolution and the Implication in the High-Temperature Catalyst Design,” ACS Applied Energy Materials. 2019. link Times cited: 15 Abstract: Bimetallic nanoparticles (NPs) are widely used in catalysis … read more USED (low confidence) J. Méndez and M. Ponga, “MXE: A package for simulating long-term diffusive mass transport phenomena in nanoscale systems,” Comput. Phys. Commun. 2019. link Times cited: 8 USED (low confidence) F. Fischer, G. Schmitz, and S. Eich, “A systematic study of grain boundary segregation and grain boundary formation energy using a new copper–nickel embedded-atom potential,” Acta Materialia. 2019. link Times cited: 32 USED (low confidence) F. Fischer, G. Schmitz, and S. Eich, “A Systematic Study of Grain Boundary Segregation and Grain Boundary Formation Energy Using a New Copper-Nickel Embedded-Atom Potential,” Computational Materials Science eJournal. 2019. link Times cited: 0 Abstract: In this atomistic study on the copper–nickel system, a new e… read more USED (low confidence) M. Dodaran, J. Wang, Y. Chen, W. Meng, and S. Shao, “Energetic, Structural and Mechanical Properties of Terraced Interfaces,” MatSciRN: Other Computational Materials Science (Topic). 2019. link Times cited: 14 USED (low confidence) H. N. Pishkenari, F. S. Yousefi, and A. Taghibakhshi, “Determination of surface properties and elastic constants of FCC metals: a comparison among different EAM potentials in thin film and bulk scale,” Materials Research Express. 2018. link Times cited: 22 Abstract: Three independent elastic constants C11, C12, and C44 were c… read more USED (low confidence) Y. Long, B. He, W. Cui, X. Zhuang, and J. Twiefel, “Molecular Dynamics Simulation of Microwelds Formation and Breakage During Ultrasonic Copper Wire Bonding,” 2018 IEEE 68th Electronic Components and Technology Conference (ECTC). 2018. link Times cited: 3 Abstract: Nowadays ultrasonic (US) copper wire bonding gests more requ… read more USED (low confidence) D. Kryzhevich, K. Zolnikov, A. Korchuganov, and S. Psakhie, “Structure of bicomponent particles synthesized from colliding metal clusters.” 2017. link Times cited: 0 USED (low confidence) M. Kozłowski, D. Scopece, J. Janczak-Rusch, L. Jeurgens, R. Abdank-Kozubski, and D. Passerone, “Validation of an Embedded-Atom Copper Classical Potential via Bulk and Nanostructure Simulations,” Diffusion Foundations. 2017. link Times cited: 0 Abstract: The validation of classical potentials for describing multic… read more USED (low confidence) K. Duan, L. Li, Y. Hu, and X. Wang, “Enhanced interfacial strength of carbon nanotube/copper nanocomposites via Ni-coating: Molecular-dynamics insights,” Physica E-low-dimensional Systems & Nanostructures. 2017. link Times cited: 31 USED (low confidence) A. Dmitriev, A. Nikonov, and W. Österle, “Molecular dynamics sliding simulations of amorphous Ni, Ni-P and nanocrystalline Ni films,” Computational Materials Science. 2017. link Times cited: 35 USED (low confidence) I. Bustamante-Romero, O. D. L. Pena-Seaman, R. Heid, and K. Bohnen, “Effect of magnetism on lattice dynamical properties in the Ni–Cu alloy from first principles,” Journal of Magnetism and Magnetic Materials. 2016. link Times cited: 4 USED (low confidence) D. Kryzhevich, A. Korchuganov, K. Zolnikov, and S. Psakhie, “Plastic deformation nucleation in elastically loaded CuNi alloy during nanoindentation.” 2016. link Times cited: 0 Abstract: The molecular dynamics simulation of the behavior of elastic… read more USED (low confidence) T. Fu et al., “Molecular dynamics simulation of nanoindentation on Cu/Ni nanotwinned multilayer films using a spherical indenter,” Scientific Reports. 2016. link Times cited: 118 USED (low confidence) S. M. Rassoulinejad-Mousavi, Y. Mao, and Y. Zhang, “Evaluation of Copper, Aluminum and Nickel Interatomic Potentials on Predicting the Elastic Properties,” arXiv: Computational Physics. 2016. link Times cited: 63 Abstract: Choice of appropriate force field is one of the main concern… read more USED (low confidence) M. Zaenudin, Kasum, A. Gamayel, and M. N. Mohammed, “Molecular dynamics simulation on the effect of grading function on mechanical properties of Cu-Ni functionally graded material alloy,” THE 11TH INTERNATIONAL CONFERENCE ON THEORETICAL AND APPLIED PHYSICS: The Spirit of Research and Collaboration Facing the COVID-19 Pandemic. 2023. link Times cited: 0 USED (low confidence) A. Nikonov, A. Dmitriev, and A. Smolin, “Selection of the potential for MD-modeling of phase martensitic transformations in Al-Cu-Ni alloy,” PROCEEDINGS OF THE INTERNATIONAL CONFERENCE “PHYSICAL MESOMECHANICS. MATERIALS WITH MULTILEVEL HIERARCHICAL STRUCTURE AND INTELLIGENT MANUFACTURING TECHNOLOGY.” 2022. link Times cited: 1 USED (low confidence) Y. Wang, J. Zuo, N. Jiang, K. Niu, and Y. Wu, “Uniaxial tension deformation study of copper/nickel laminated composites: Effects of lamella number and interlamellar spacing,” Computational Materials Science. 2020. link Times cited: 10 USED (low confidence) A. Esfandiarpour and M. N. Nasrabadi, “Investigation of the effect of composing elements of CuNiCoFeV high entropy alloy on thermal-elastic properties: An ab initio study,” Intermetallics. 2019. link Times cited: 8 USED (low confidence) W. Nöhring, “Dislocation Cross-Slip in Face-Centered Cubic Solid Solution Alloys.” 2018. link Times cited: 2 Abstract: The mechanical strength of metals depends on their resistanc… read more USED (low confidence) D. Kryzhevich, K. Zolnikov, A. Korchuganov, and S. Psakhie, “Nanopowder synthesis based on electric explosion technology.” 2017. link Times cited: 2 NOT USED (low confidence) A. Hernandez and T. Mueller, “Generalizability of Functional Forms for Interatomic Potential Models Discovered by Symbolic Regression,” ArXiv. 2022. link Times cited: 0 Abstract: In recent years there has been great progress in the use of … read more NOT USED (low confidence) B. Yao, Z. R. Liu, and R. F. Zhang, “EAPOTc: An integrated empirical interatomic potential optimization platform for compound solids,” Computational Materials Science. 2022. link Times cited: 1 NOT USED (low confidence) Z. R. Liu, B. Yao, and R. F. Zhang, “SPaMD studio: An integrated platform for atomistic modeling, simulation, analysis, and visualization,” Computational Materials Science. 2021. link Times cited: 7 NOT USED (high confidence) K. Moldosanov et al., “Terahertz-to-infrared converters for imaging the human skin cancer: challenges and feasibility,” Journal of Medical Imaging. 2023. link Times cited: 2 Abstract: Abstract. Purpose Terahertz (THz) medical imaging is a promi… read more NOT USED (high confidence) L. Xu, L. Casillas-Trujillo, Y. Gao, and H. Xu, “Compositional effects on stacking fault energies in Ni-based alloys using first-principles and atomistic simulations,” Computational Materials Science. 2021. link Times cited: 5 NOT USED (high confidence) K. Kasum, F. Mulyana, M. Zaenudin, A. Gamayel, and M. Mohammed, “Molecular Dynamics Simulation on Creep Mechanism of Nanocrystalline Cu-Ni Alloy.” 2021. link Times cited: 3 Abstract: Creep mechanism is an essential mechanism for material when … read more NOT USED (high confidence) J. Alberdi-Rodriguez, S. Acharya, T. Rahman, A. Arnau, and M. Gosálvez, “Dominant contributions to the apparent activation energy in two-dimensional submonolayer growth: comparison between Cu/Ni(111) and Ni/Cu(111),” Journal of Physics: Condensed Matter. 2020. link Times cited: 0 Abstract: For surface-mediated processes in general, such as epitaxial… read more NOT USED (high confidence) A. Markidonov, M. Starostenkov, P. Zakharov, D. Lubyanoi, and V. N. Lipunov, “Emission of Dislocation Loops from Nanovoids in an FCC Crystal Subjected to Shear Deformation under Post-Cascade Shock Waves,” Journal of Experimental and Theoretical Physics. 2019. link Times cited: 3 NOT USED (high confidence) M. Islam, M. S. H. Thakur, S. Mojumder, A. A. Amin, and M. M. Islam, “Mechanical and vibrational characteristics of functionally graded Cu–Ni nanowire: A molecular dynamics study,” Composites Part B-engineering. 2019. link Times cited: 27 NOT USED (high confidence) C. Wu, T. Fang, and Y.-J. Lin, “Quasi-continuum simulations of side-to-side nanowelding of metals,” Journal of Molecular Modeling. 2018. link Times cited: 2 NOT USED (high confidence) Q. Zhang et al., “Microstructure and nanoindentation behavior of Cu composites reinforced with graphene nanoplatelets by electroless co-deposition technique,” Scientific Reports. 2017. link Times cited: 54 NOT USED (high confidence) W. Nöhring and W. Curtin, “Dislocation cross-slip in fcc solid solution alloys,” Acta Materialia. 2017. link Times cited: 65 NOT USED (high confidence) H. Mu, B. Xu, C. Ouyang, and X. Lei, “Highly optimized embedding atom method potential for Pt-Cu alloys,” Journal of Alloys and Compounds. 2017. link Times cited: 6 NOT USED (high confidence) B. Onat and S. Durukanoğlu, “The role of vibrations in thermodynamic properties of Cu-Ni alloys,” The European Physical Journal B. 2014. link Times cited: 8 NOT USED (high confidence) C. Galvin, R. Grimes, and P. Burr, “A molecular dynamics method to identify the liquidus and solidus in a binary phase diagram,” Computational Materials Science. 2021. link Times cited: 6 NOT USED (definite) A. Hernandez, A. Balasubramanian, F. Yuan, S. Mason, and T. Mueller, “Fast, accurate, and transferable many-body interatomic potentials by symbolic regression,” npj Computational Materials. 2019. link Times cited: 51 |
| Funding | Not available |
| Short KIM ID
The unique KIM identifier code.
| MO_592013496703_005 |
| Extended KIM ID
The long form of the KIM ID including a human readable prefix (100 characters max), two underscores, and the Short KIM ID. Extended KIM IDs can only contain alpha-numeric characters (letters and digits) and underscores and must begin with a letter.
| EAM_Dynamo_OnatDurukanoglu_2014_CuNi__MO_592013496703_005 |
| DOI |
10.25950/e2733dc9 https://doi.org/10.25950/e2733dc9 https://commons.datacite.org/doi.org/10.25950/e2733dc9 |
| KIM Item Type
Specifies whether this is a Portable Model (software implementation of an interatomic model); Portable Model with parameter file (parameter file to be read in by a Model Driver); Model Driver (software implementation of an interatomic model that reads in parameters).
| Portable Model using Model Driver EAM_Dynamo__MD_120291908751_005 |
| Driver | EAM_Dynamo__MD_120291908751_005 |
| KIM API Version | 2.0 |
| Potential Type | eam |
| Previous Version | EAM_Dynamo_OnatDurukanoglu_2014_CuNi__MO_592013496703_004 |
| Grade | Name | Category | Brief Description | Full Results | Aux File(s) |
|---|---|---|---|---|---|
| P | vc-species-supported-as-stated | mandatory | The model supports all species it claims to support; see full description. |
Results | Files |
| P | vc-periodicity-support | mandatory | Periodic boundary conditions are handled correctly; see full description. |
Results | Files |
| P | vc-permutation-symmetry | mandatory | Total energy and forces are unchanged when swapping atoms of the same species; see full description. |
Results | Files |
| A | vc-forces-numerical-derivative | consistency | Forces computed by the model agree with numerical derivatives of the energy; see full description. |
Results | Files |
| F | vc-dimer-continuity-c1 | informational | The energy versus separation relation of a pair of atoms is C1 continuous (i.e. the function and its first derivative are continuous); see full description. |
Results | Files |
| P | vc-objectivity | informational | Total energy is unchanged and forces transform correctly under rigid-body translation and rotation; see full description. |
Results | Files |
| P | vc-inversion-symmetry | informational | Total energy is unchanged and forces change sign when inverting a configuration through the origin; see full description. |
Results | Files |
| P | vc-memory-leak | informational | The model code does not have memory leaks (i.e. it releases all allocated memory at the end); see full description. |
Results | Files |
| P | vc-thread-safe | mandatory | The model returns the same energy and forces when computed in serial and when using parallel threads for a set of configurations. Note that this is not a guarantee of thread safety; see full description. |
Results | Files |
| P | vc-unit-conversion | mandatory | The model is able to correctly convert its energy and/or forces to different unit sets; see full description. |
Results | Files |
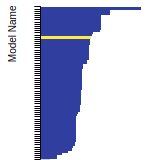
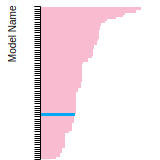
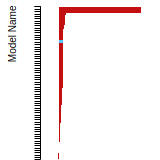
BCC Lattice Constant
This bar chart plot shows the mono-atomic body-centered cubic (bcc) lattice constant predicted by the current model (shown in the unique color) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
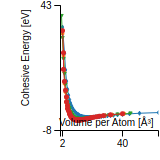
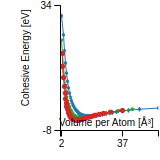
Cohesive Energy Graph
This graph shows the cohesive energy versus volume-per-atom for the current mode for four mono-atomic cubic phases (body-centered cubic (bcc), face-centered cubic (fcc), simple cubic (sc), and diamond). The curve with the lowest minimum is the ground state of the crystal if stable. (The crystal structure is enforced in these calculations, so the phase may not be stable.) Graphs are generated for each species supported by the model.
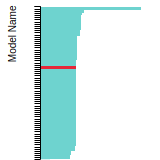
Diamond Lattice Constant
This bar chart plot shows the mono-atomic face-centered diamond lattice constant predicted by the current model (shown in the unique color) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
Dislocation Core Energies
This graph shows the dislocation core energy of a cubic crystal at zero temperature and pressure for a specific set of dislocation core cutoff radii. After obtaining the total energy of the system from conjugate gradient minimizations, non-singular, isotropic and anisotropic elasticity are applied to obtain the dislocation core energy for each of these supercells with different dipole distances. Graphs are generated for each species supported by the model.
(No matching species)FCC Elastic Constants
This bar chart plot shows the mono-atomic face-centered cubic (fcc) elastic constants predicted by the current model (shown in blue) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
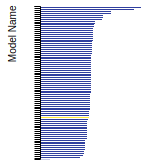
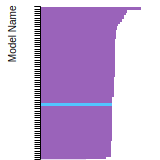
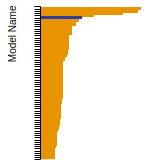
FCC Lattice Constant
This bar chart plot shows the mono-atomic face-centered cubic (fcc) lattice constant predicted by the current model (shown in red) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
FCC Stacking Fault Energies
This bar chart plot shows the intrinsic and extrinsic stacking fault energies as well as the unstable stacking and unstable twinning energies for face-centered cubic (fcc) predicted by the current model (shown in blue) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
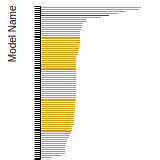
FCC Surface Energies
This bar chart plot shows the mono-atomic face-centered cubic (fcc) relaxed surface energies predicted by the current model (shown in blue) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
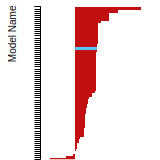
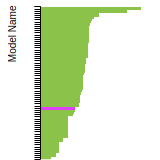
SC Lattice Constant
This bar chart plot shows the mono-atomic simple cubic (sc) lattice constant predicted by the current model (shown in the unique color) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
Cubic Crystal Basic Properties Table
Species: CuSpecies: Ni
Disclaimer From Model Developer
This potential is tabulated using more spline points to provide smoother cutoff and better accuracy for simulations.
Creators:
Contributor: karls
Publication Year: 2019
DOI: https://doi.org/10.25950/64cb38c5
This Test Driver uses LAMMPS to compute the cohesive energy of a given monoatomic cubic lattice (fcc, bcc, sc, or diamond) at a variety of lattice spacings. The lattice spacings range from a_min (=a_min_frac*a_0) to a_max (=a_max_frac*a_0) where a_0, a_min_frac, and a_max_frac are read from stdin (a_0 is typically approximately equal to the equilibrium lattice constant). The precise scaling and number of lattice spacings sampled between a_min and a_0 (a_0 and a_max) is specified by two additional parameters passed from stdin: N_lower and samplespacing_lower (N_upper and samplespacing_upper). Please see README.txt for further details.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Cohesive energy versus lattice constant curve for bcc Cu v004 | view | 12074 | |
| Cohesive energy versus lattice constant curve for bcc Ni v004 | view | 11876 | |
| Cohesive energy versus lattice constant curve for diamond Cu v004 | view | 12134 | |
| Cohesive energy versus lattice constant curve for diamond Ni v004 | view | 11866 | |
| Cohesive energy versus lattice constant curve for fcc Cu v004 | view | 11816 | |
| Cohesive energy versus lattice constant curve for fcc Ni v004 | view | 18785 | |
| Cohesive energy versus lattice constant curve for sc Cu v004 | view | 15952 | |
| Cohesive energy versus lattice constant curve for sc Ni v004 | view | 22065 |
Creators: Junhao Li and Ellad Tadmor
Contributor: tadmor
Publication Year: 2019
DOI: https://doi.org/10.25950/5853fb8f
Computes the cubic elastic constants for some common crystal types (fcc, bcc, sc, diamond) by calculating the hessian of the energy density with respect to strain. An estimate of the error associated with the numerical differentiation performed is reported.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Elastic constants for bcc Cu at zero temperature v006 | view | 6846 | |
| Elastic constants for bcc Ni at zero temperature v006 | view | 5918 | |
| Elastic constants for fcc Cu at zero temperature v006 | view | 1887 | |
| Elastic constants for fcc Ni at zero temperature v006 | view | 2431 | |
| Elastic constants for sc Cu at zero temperature v006 | view | 1823 | |
| Elastic constants for sc Ni at zero temperature v006 | view | 1887 |
Creators: Junhao Li
Contributor: jl2922
Publication Year: 2019
DOI: https://doi.org/10.25950/d794c746
Computes the elastic constants for hcp crystals by calculating the hessian of the energy density with respect to strain. An estimate of the error associated with the numerical differentiation performed is reported.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Elastic constants for hcp Cu at zero temperature v004 | view | 1592 | |
| Elastic constants for hcp Ni at zero temperature v004 | view | 2006 |
Creators:
Contributor: ilia
Publication Year: 2023
DOI: https://doi.org/10.25950/e8a7ed84
Computes the equilibrium crystal structure and energy for an arbitrary crystal at zero temperature and applied stress by performing symmetry-constrained relaxation. The crystal structure is specified using the AFLOW prototype designation. Multiple sets of free parameters corresponding to the crystal prototype may be specified as initial guesses for structure optimization. No guarantee is made regarding the stability of computed equilibria, nor that any are the ground state.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Equilibrium crystal structure and energy for Cu in AFLOW crystal prototype A_cF4_225_a v001 | view | 83338 | |
| Equilibrium crystal structure and energy for Cu in AFLOW crystal prototype A_cI2_229_a v001 | view | 78406 |
Creators:
Contributor: ilia
Publication Year: 2024
DOI: https://doi.org/10.25950/2f2c4ad3
Computes the equilibrium crystal structure and energy for an arbitrary crystal at zero temperature and applied stress by performing symmetry-constrained relaxation. The crystal structure is specified using the AFLOW prototype designation. Multiple sets of free parameters corresponding to the crystal prototype may be specified as initial guesses for structure optimization. No guarantee is made regarding the stability of computed equilibria, nor that any are the ground state.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Equilibrium crystal structure and energy for Ni in AFLOW crystal prototype A_cF4_225_a v002 | view | 56811 | |
| Equilibrium crystal structure and energy for Ni in AFLOW crystal prototype A_cI2_229_a v002 | view | 55352 | |
| Equilibrium crystal structure and energy for Ni in AFLOW crystal prototype A_hP2_194_c v002 | view | 62209 |
Creators:
Contributor: brunnels
Publication Year: 2022
DOI: https://doi.org/10.25950/2c59c9d6
Computes grain boundary energy for a range of tilt angles given a crystal structure, tilt axis, and material.
Creators: Daniel S. Karls and Junhao Li
Contributor: karls
Publication Year: 2019
DOI: https://doi.org/10.25950/2765e3bf
Equilibrium lattice constant and cohesive energy of a cubic lattice at zero temperature and pressure.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Equilibrium zero-temperature lattice constant for bcc Cu v007 | view | 2335 | |
| Equilibrium zero-temperature lattice constant for bcc Ni v007 | view | 2687 | |
| Equilibrium zero-temperature lattice constant for diamond Cu v007 | view | 3487 | |
| Equilibrium zero-temperature lattice constant for diamond Ni v007 | view | 3391 | |
| Equilibrium zero-temperature lattice constant for fcc Cu v007 | view | 3999 | |
| Equilibrium zero-temperature lattice constant for fcc Ni v007 | view | 3167 | |
| Equilibrium zero-temperature lattice constant for sc Cu v007 | view | 2399 | |
| Equilibrium zero-temperature lattice constant for sc Ni v007 | view | 2463 |
Creators: Daniel S. Karls and Junhao Li
Contributor: karls
Publication Year: 2019
DOI: https://doi.org/10.25950/c339ca32
Calculates lattice constant of hexagonal bulk structures at zero temperature and pressure by using simplex minimization to minimize the potential energy.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Equilibrium lattice constants for hcp Cu v005 | view | 38331 | |
| Equilibrium lattice constants for hcp Ni v005 | view | 32186 |
Creators: Mingjian Wen
Contributor: mjwen
Publication Year: 2019
DOI: https://doi.org/10.25950/fc69d82d
This Test Driver uses LAMMPS to compute the linear thermal expansion coefficient at a finite temperature under a given pressure for a cubic lattice (fcc, bcc, sc, diamond) of a single given species.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Linear thermal expansion coefficient of fcc Cu at 293.15 K under a pressure of 0 MPa v001 | view | 10602978 |
Creators:
Contributor: mjwen
Publication Year: 2024
DOI: https://doi.org/10.25950/9d9822ec
This Test Driver uses LAMMPS to compute the linear thermal expansion coefficient at a finite temperature under a given pressure for a cubic lattice (fcc, bcc, sc, diamond) of a single given species.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Linear thermal expansion coefficient of fcc Ni at 293.15 K under a pressure of 0 MPa v002 | view | 1327157 |
Creators: Matt Bierbaum
Contributor: mattbierbaum
Publication Year: 2019
DOI: https://doi.org/10.25950/64f4999b
Calculates the phonon dispersion relations for fcc lattices and records the results as curves.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Phonon dispersion relations for fcc Cu v004 | view | 46480 | |
| Phonon dispersion relations for fcc Ni v004 | view | 50607 |
Creators:
Contributor: SubrahmanyamPattamatta
Publication Year: 2019
DOI: https://doi.org/10.25950/b4cfaf9a
Intrinsic and extrinsic stacking fault energies, unstable stacking fault energy, unstable twinning energy, stacking fault energy as a function of fractional displacement, and gamma surface for a monoatomic FCC lattice at zero temperature and pressure.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Stacking and twinning fault energies for fcc Cu v002 | view | 9463914 | |
| Stacking and twinning fault energies for fcc Ni v002 | view | 8938046 |
Creators: Matt Bierbaum
Contributor: mattbierbaum
Publication Year: 2019
DOI: https://doi.org/10.25950/6c43a4e6
Calculates the surface energy of several high symmetry surfaces and produces a broken-bond model fit. In latex form, the fit equations are given by:
E_{FCC} (\vec{n}) = p_1 (4 \left( |x+y| + |x-y| + |x+z| + |x-z| + |z+y| +|z-y|\right)) + p_2 (8 \left( |x| + |y| + |z|\right)) + p_3 (2 ( |x+ 2y + z| + |x+2y-z| + |x-2y + z| + |x-2y-z| + |2x+y+z| + |2x+y-z| +|2x-y+z| +|2x-y-z| +|x+y+2z| +|x+y-2z| +|x-y+2z| +|x-y-2z| ) + c
E_{BCC} (\vec{n}) = p_1 (6 \left( | x+y+z| + |x+y-z| + |-x+y-z| + |x-y+z| \right)) + p_2 (8 \left( |x| + |y| + |z|\right)) + p_3 (4 \left( |x+y| + |x-y| + |x+z| + |x-z| + |z+y| +|z-y|\right)) +c.
In Python, these two fits take the following form:
def BrokenBondFCC(params, index):
import numpy
x, y, z = index
x = x / numpy.sqrt(x**2.+y**2.+z**2.)
y = y / numpy.sqrt(x**2.+y**2.+z**2.)
z = z / numpy.sqrt(x**2.+y**2.+z**2.)
return params[0]*4* (abs(x+y) + abs(x-y) + abs(x+z) + abs(x-z) + abs(z+y) + abs(z-y)) + params[1]*8*(abs(x) + abs(y) + abs(z)) + params[2]*(abs(x+2*y+z) + abs(x+2*y-z) +abs(x-2*y+z) +abs(x-2*y-z) + abs(2*x+y+z) +abs(2*x+y-z) +abs(2*x-y+z) +abs(2*x-y-z) + abs(x+y+2*z) +abs(x+y-2*z) +abs(x-y+2*z) +abs(x-y-2*z))+params[3]
def BrokenBondBCC(params, x, y, z):
import numpy
x, y, z = index
x = x / numpy.sqrt(x**2.+y**2.+z**2.)
y = y / numpy.sqrt(x**2.+y**2.+z**2.)
z = z / numpy.sqrt(x**2.+y**2.+z**2.)
return params[0]*6*(abs(x+y+z) + abs(x-y-z) + abs(x-y+z) + abs(x+y-z)) + params[1]*8*(abs(x) + abs(y) + abs(z)) + params[2]*4* (abs(x+y) + abs(x-y) + abs(x+z) + abs(x-z) + abs(z+y) + abs(z-y)) + params[3]
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Broken-bond fit of high-symmetry surface energies in fcc Cu v004 | view | 31829 | |
| Broken-bond fit of high-symmetry surface energies in fcc Ni v004 | view | 29462 |
Creators:
Contributor: efuem
Publication Year: 2023
DOI: https://doi.org/10.25950/fca89cea
Computes the monovacancy formation energy and relaxation volume for cubic and hcp monoatomic crystals.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Monovacancy formation energy and relaxation volume for fcc Cu | view | 482067 | |
| Monovacancy formation energy and relaxation volume for fcc Ni | view | 564669 |
Creators:
Contributor: efuem
Publication Year: 2023
DOI: https://doi.org/10.25950/c27ba3cd
Computes the monovacancy formation and migration energies for cubic and hcp monoatomic crystals.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Vacancy formation and migration energy for fcc Cu | view | 1891016 | |
| Vacancy formation and migration energy for fcc Ni | view | 1099964 |
| Test | Error Categories | Link to Error page |
|---|---|---|
| Elastic constants for diamond Cu at zero temperature v001 | other | view |
| Elastic constants for diamond Ni at zero temperature v001 | other | view |
No Driver
| Verification Check | Error Categories | Link to Error page |
|---|---|---|
| MemoryLeak__VC_561022993723_004 | other | view |
| EAM_Dynamo_OnatDurukanoglu_2014_CuNi__MO_592013496703_005.txz | Tar+XZ | Linux and OS X archive |
| EAM_Dynamo_OnatDurukanoglu_2014_CuNi__MO_592013496703_005.zip | Zip | Windows archive |
This Model requires a Model Driver. Archives for the Model Driver EAM_Dynamo__MD_120291908751_005 appear below.
| EAM_Dynamo__MD_120291908751_005.txz | Tar+XZ | Linux and OS X archive |
| EAM_Dynamo__MD_120291908751_005.zip | Zip | Windows archive |