Citations
This panel presents information regarding the papers that have cited the interatomic potential (IP) whose page you are on.
The OpenKIM machine learning based Deep Citation framework is used to determine whether the citing article actually used the IP in computations (denoted by "USED") or only provides it as a background citation (denoted by "NOT USED"). For more details on Deep Citation and how to work with this panel, click the documentation link at the top of the panel.
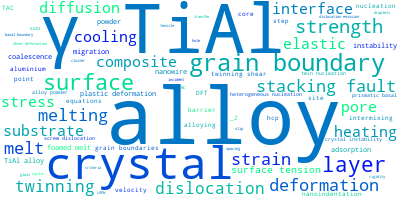
The word cloud to the right is generated from the abstracts of IP principle source(s) (given below in "How to Cite") and the citing articles that were determined to have used the IP in order to provide users with a quick sense of the types of physical phenomena to which this IP is applied.
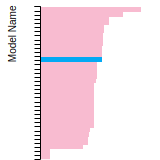
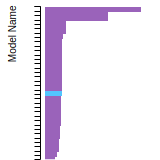
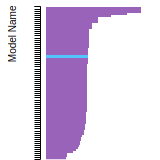
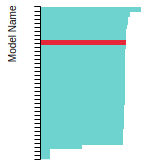
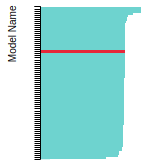
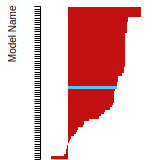
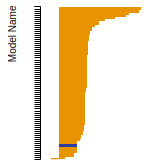
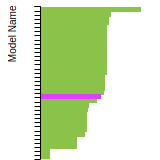
The bar chart shows the number of articles that cited the IP per year. Each bar is divided into green (articles that USED the IP) and blue (articles that did NOT USE the IP).
Users are encouraged to correct Deep Citation errors in determination by clicking the speech icon next to a citing article and providing updated information. This will be integrated into the next Deep Citation learning cycle, which occurs on a regular basis.
OpenKIM acknowledges the support of the Allen Institute for AI through the Semantic Scholar project for providing citation information and full text of articles when available, which are used to train the Deep Citation ML algorithm.
|
This panel provides information on past usage of this interatomic potential (IP) powered by the OpenKIM Deep Citation framework. The word cloud indicates typical applications of the potential. The bar chart shows citations per year of this IP (bars are divided into articles that used the IP (green) and those that did not (blue)). The complete list of articles that cited this IP is provided below along with the Deep Citation determination on usage. See the Deep Citation documentation for more information.
453 Citations (370 used)
Help us to determine which of the papers that cite this potential actually used it to perform calculations. If you know, click the .
USED (high confidence) S. Surulere, M. Shatalov, and E. Olayiwola, “Optimal interatomic potentials using modified method of least squares: Optimal form of interatomic potentials,” Open Physics. 2023. link Times cited: 0 Abstract: The problem of optimization of interatomic potentials is for… read moreAbstract: The problem of optimization of interatomic potentials is formulated and solved by means of generalization of the Morse, Kaxiras–Pandey, and Rydberg potentials. The interatomic potentials are treated as solutions of some second-order ordinary differential equations which will be classified and analyzed. The most appropriate analytic form of the understudied potentials will be proposed based on a one-dimensional search for the parameter, γ \gamma , which is the power of the interatomic distance, r r . The optimal analytic form will also be proposed for metals such as gold, copper, aluminium, titanium, and the silver–copper alloy. The method of least squares will be used to estimate the potential parameters. Phenomenological potentials such as the classical Rydberg, classical Morse, generalized Morse, Kaxiras–Pandey, and classical Lennard–Jones will be studied, and new potentials based on the combination of some of the aforementioned potentials will also be proposed. Metrics such as the goal function values, will be used to identify which optimal value of the parameter, γ \gamma , is most appropriate to introduce into the preferred interatomic potential for interaction between atoms. read less USED (high confidence) C. Li et al., “Ultrafast modulation of the molten metal surface tension under femtosecond laser irradiation,” Chinese Physics Letters. 2022. link Times cited: 1 Abstract:
We predict ultrafast modulation of the pure molten metal s… read moreAbstract:
We predict ultrafast modulation of the pure molten metal surface stress fields under the irradiation of the single femtosecond laser pulse through the two-temperature model molecular-dynamics simulations. High-resolution and precision calculations are used to resolve the ultrafast laser-induced anisotropic relaxations of the pressure components on the time-scale comparable to the intrinsic liquid density relaxation time. The magnitudes of the dynamic surface tensions are found being modulated sharply within picoseconds after the irradiation, due to the development of the nanometer scale non-hydrostatic regime behind the exterior atomic layer of the liquid surfaces. The reported novel regulation mechanism of the liquid surface stress field and the dynamic surface tension hints at levitating the manipulation of liquid surfaces, such as ultrafast steering the surface directional transport and patterning. read less USED (high confidence) Z. Sun, J. Zhang, G. Xin, L. Xie, L. Yang, and Q. Peng, “Tensile mechanical properties of CoCrFeNiTiAl high entropy alloy via molecular dynamics simulations,” Intermetallics. 2022. link Times cited: 18 USED (high confidence) P. Polyakova, S. Shcherbinin, and J. Baimova, “Molecular dynamics investigation of atomic mixing and mechanical properties of Al / Ti interface,” Letters on Materials. 2021. link Times cited: 2 Abstract: With the urgent lightweight demand in the aerospace engineer… read moreAbstract: With the urgent lightweight demand in the aerospace engineering and transportation industries, Al / Ti composite structures have attracted much interest due to their excellent performances compared with conventional materials. Computational simulations have contributed to the understanding of both fundamental and practical aspects of fabrication of such composites and studying of their properties. The present work reports the results of studies based on molecular dynamics simulations on the mechanical properties of an Al / Ti composite obtained by compression combined with shear strain. Tensile properties of a nanosized Ti / Al composite consisting of two single crystals obtained after different compression rates are analyzed. The loading scheme applied in the present work is a simplification of the scenario experimentally realized previously to obtain Al-matrix composites. It is confirmed that uniaxial compression combined with shear deformation is an effective way to obtain the composite structure since severe plastic deformation facilitates the diffusion process. The results indicated that a symmetrical atomic movement took place in the Ti / Al interface during deformation. However, Al atoms diffuse into the Ti block easier than Ti atoms into the Al block. Tensile tests showed that fracture took place in the Al part of the final composite sample, which means that the interlayer region where the mixing of Ti and Al atoms is observed is stronger than the pure Al part. read less USED (high confidence) F. Baras, Q. Bizot, A. Fourmont, S. L. Gallet, and O. Politano, “Mechanical activation of metallic powders and reactivity of activated nanocomposites: a molecular dynamics approach,” Applied Physics A. 2021. link Times cited: 1 USED (high confidence) H. Xiang and W. Guo, “Post-yielding dislocation retraction of nano-lamellar TiAl single crystals,” Science China Physics, Mechanics & Astronomy. 2021. link Times cited: 7 USED (high confidence) T. Sun, A. Tu, H. Wang, S.-J. Li, H. Peng, and J.-ping Li, “Uniaxial Strain-Induced Grain Boundary Migration in Titanium,” Acta Metallurgica Sinica (English Letters). 2021. link Times cited: 3 USED (high confidence) Z. Fan, H. Men, Y. Wang, and Z. Que, “A New Atomistic Mechanism for Heterogeneous Nucleation in the Systems with Negative Lattice Misfit: Creating a 2D Template for Crystal Growth.” 2021. link Times cited: 21 Abstract: Heterogeneous nucleation is a widespread phenomenon in both … read moreAbstract: Heterogeneous nucleation is a widespread phenomenon in both nature and technology. However, our current understanding is largely confined to the classical nucleation theory (CNT) postulated over a century ago, in which heterogeneous nucleation occurs stochastically to form a spherical cap facilitated by a substrate. In this paper, we show that heterogeneous nucleation in systems with negative lattice misfit completes deterministically within three atomic layers by structural templating to form a two-dimentional template from which the new phase can grow. Using molecular dynamics (MD) simulations of a generic system containing metallic liquid (Al) and a substrate of variable lattice misfit (fcc lattice with fixed Al atoms), we found that heterogeneous nucleation proceeds layer-by-layer: the first layer accommodates misfit through a partial edge dislocation network; the second layer twists an angle through a partial screw dislocation network to reduce lattice distortion; and the third layer creates a crystal plane of the solid (the 2D nucleus) that templates further growth. The twist angle of the solid relative to the substrate as a signature of heterogeneous nucleation in the systems with negative lattice misfit has been validated by high resolution transmission electron microscopic (HRTEM) examination of TiB2/Al and TiB2/α-Al15(Fe, Mn)3Si2 interfaces in two different Al-alloys. read less USED (high confidence) Z. Cui, X. Zhou, and Q. Meng, “Atomic-Scale Mechanism Investigation of Mass Transfer in Laser Fabrication Process of Ti-Al Alloy via Molecular Dynamics Simulation,” Metals. 2020. link Times cited: 6 Abstract: This article deals with a Ti-Al alloy system. Molecular dyna… read moreAbstract: This article deals with a Ti-Al alloy system. Molecular dynamics simulation was used to simulate and explore the mass transfer behavior during the laser fabrication process at atomic scale. The research goal is to investigate the mass transfer mechanism at atomic scale and the movement of solute atoms during the laser fabrication process. The mean square displacement (MSD), radial distribution function (RDF), atomic number density, and atomic displacement vector were calculated to characterize it. The results show that the TiAl alloy is completely melted when heated up to 2400 K, and increasing the temperature past 2400 K has little effect on mass transfer. As the heating time increases, the diffusion coefficient gradually decreases, the diffusion weakens, and the mass transfer process gradually stabilizes. In Ti-Al binary alloys, the diffusion coefficients of different solute atoms are related to the atomic fraction. During the melting process, the alloy particle system has a greater diffusion coefficient than the elemental particle system. read less USED (high confidence) A. Neogi, M. Alam, A. Hartmaier, and R. Janisch, “Anisotropic failure behavior of ordered intermetallic TiAl alloys under pure mode-I loading,” Modelling and Simulation in Materials Science and Engineering. 2020. link Times cited: 13 Abstract: Whether a metallic material fractures by brittle cleavage or… read moreAbstract: Whether a metallic material fractures by brittle cleavage or by ductile rupture is primarily governed by the competition between cleavage and dislocation emission at the crack tip. The linear elastic fracture mechanics (LEFM) based criterion of Griffith, respectively the one for dislocation emission of Rice, are sufficiently reliable for determining the possible crack tip propagation mechanisms in isotropic crystalline metals. However, the applicability of these criteria is questionable when non-cubic, anisotropic solids are considered, as e.g. ordered intermetallic TiAl phases, where slip systems are limited and elastic anisotropy is pronounced. We study brittle versus ductile failure mechanisms in face-centered tetragonal TiAl and hexagonal Ti3Al using large-scale atomistic simulations and compare our findings to the predictions of LEFM-based criteria augmented by elastic anisotropy. We observe that the augmented Griffith and Rice criteria are reliable for determining the direction dependent crack tip mechanisms, if all the available dislocation slip systems are taken into account. Yet, atomistic simulations are necessary to understand crack blunting due to mixed mechanisms, or shear instabilities other than dislocation emission. The results of our systematic study can be used as basis for modifications of the Griffith/Rice criteria in order to incorporate such effects. read less USED (high confidence) Y.-C. Hu, K. Zhang, S. A. Kube, J. Schroers, M. Shattuck, and C. O’Hern, “Glass formation in binary alloys with different atomic symmetries,” arXiv: Materials Science. 2020. link Times cited: 4 Abstract: Prediction of the glass forming ability (GFA) of alloys rema… read moreAbstract: Prediction of the glass forming ability (GFA) of alloys remains a major challenge. We are not able to predict the composition dependence of the GFA of even binary alloys. To investigate the effect of each element's propensity to form particular crystal structures on glass formation, we focus on binary alloys composed of elements with the same size, but different atomic symmetries using the patchy-particle model. For mixtures with atomic symmetries that promote different crystal structures, the minimum critical cooling rate $R_c$ is only a factor of $5$ lower than that for the pure substances. For mixtures with different atomic symmetries that promote local crystalline and icosahedral order, the minimum $R_c$ is more than $3$ orders of magnitude lower than that for pure substances. Results for $R_c$ for the patchy-particle model are in agreement with those from embedded atom method simulations and sputtering experiments of NiCu, TiAl, and high entropy alloys. read less USED (high confidence) Q. Bizot, O. Politano, A. Nepapushev, S. Vadchenko, A. Rogachev, and F. Baras, “Reactivity of the Ti–Al system: Experimental study and molecular dynamics simulations,” Journal of Applied Physics. 2020. link Times cited: 11 Abstract: The reactivity of the Ti–Al system was investigated experime… read moreAbstract: The reactivity of the Ti–Al system was investigated experimentally in the case of reactive laminated particles produced by high energy ball milling. The ignition temperature for a self-sustaining reaction was measured as a function of the heating rate. By means of the Kissinger analysis, two activation energies were evaluated. The first one is associated with the solid-state transformation at the interface below the melting point of Al. The second one corresponds to the exothermic dissolution of Ti into Al liquid together with the formation of TiAl 3. A complementary microscopic approach was developed in order to detect all elemental processes associated with the reactivity of the Ti–Al system in composite materials. Above the melting temperature of Al, the exothermic dissolution of Ti into the liquid layer starts and induces a self-sustaining behavior until the reaction is complete. The dissolution step is limited by the low solubility of Ti in Al. The formation of the intermetallic compound TiAl 3 was o... read less USED (high confidence) S. Subedi, L. Morrissey, S. M. Handrigan, and S. Nakhla, “The effect of many-body potential type and parameterisation on the accuracy of predicting mechanical properties of aluminium using molecular dynamics,” Molecular Simulation. 2020. link Times cited: 8 Abstract: ABSTRACT As opposed to traditional laboratory testing, Molec… read moreAbstract: ABSTRACT As opposed to traditional laboratory testing, Molecular Dynamics (MD) offers an atomistic scale method to estimate the mechanical properties of metals. However, there is limited literature that shows the effect of interatomic potentials when determining mechanical properties. Hence, the present research was conducted to investigate the accuracy of various interatomic potentials in estimating mechanical properties of aluminium. Several types of potentials, including Embedded Atom Method (EAM), Modified EAM (MEAM) and Reactive Force Field (ReaxFF) were compared with available experimental data for pure aluminium to determine the most accurate interatomic potential. A uniaxial tensile test was performed at room temperature using MD simulations for nanoscale aluminium. Results demonstrated that those potentials parameterised with elastic constants at physically realisable temperatures were consistently more accurate. Overall, the Mishin et al. EAM potential was the most accurate when compared to single-crystal experimental values. Regardless of the potential type, the error was significantly higher for those potentials that did not consider elastic constants during development. In brief, the application of the interatomic potentials to estimate mechanical properties of a nanoscale aluminium was investigated. read less USED (high confidence) D. Peng, W. Fu, and X. Yang, “Molecular Dynamics Simulations of Ti Crystallization with Solid–Liquid Configuration Method,” Physics of the Solid State. 2019. link Times cited: 1 USED (high confidence) A. Zinovev, A. Iskandarov, S. Dmitriev, and A. Pshenichnyuk, “Criteria of instability of copper and aluminium perfect crystals subjected to elastic deformation in the temperature range 0 – 400 K,” Letters on Materials. 2019. link Times cited: 1 Abstract: Polycrystalline metals have flow stress two to three orders … read moreAbstract: Polycrystalline metals have flow stress two to three orders of magnitude lower than the theoretical shear strength estimated by Frenkel model. This significant strength difference is primarily due to the presence of defects, such as dislocations and grain boundaries. However, it was experimentally found that defect-free nanoscale objects (whiskers, nanopillars, etc.) can exhibit strength close to the theoretical limit. With the development of nanotechnology, interest in the study of the theoretical strength of metals and alloys has grown significantly. It is important to find reliable criteria of lattice instability when homogeneous nucleation of defects begins during deformation of an ideal crystal lattice. Note that the Frenkel estimation does not take into account thermal vibrations of atoms and attempts are being made to take into account the effect of temperature on the theoretical strength of defect-free crystals. In this paper, using molecular dynamics simulation, we study shear deformation in the direction of ( )[ ] 111 112 for single crystals of copper and aluminum in the temperature range from 0 to 400 K. Lattice instability was evaluated using two criteria: (i) macroscopic criterion, which is related to the loss of positive definiteness of the stiffness tensor, and (ii) a microscopic criterion related to the formation of a stacking fault, which leads to a drop of the applied shear stress. It was demonstrated that both criteria are consistent at low temperatures, but the macroscopic criterion is less reliable at higher temperatures. read less USED (high confidence) N. Zhou, G. Zhang, T. Guo, X. Guo, S. Tang, and X. Huang, “twin nucleation at prismatic/basal boundary in hexagonal close-packed metals,” Philosophical Magazine. 2019. link Times cited: 7 Abstract: ABSTRACT This paper examines {10} twin nucleation and growth… read moreAbstract: ABSTRACT This paper examines {10} twin nucleation and growth under uniaxial tension at the prismatic/basal boundary through both molecular dynamics simulations and continuum mechanics modelling. Our results show that two disconnection dipoles exist on every intrinsic prismatic plane of the crystal which constructs the prismatic/basal boundary. Only one of the two disconnection dipoles is at the nucleus of {10} twins. The disconnection is activated and glides plane-by-plane along the direction throughout twin growth. The prismatic plane of the matrix is converted to the basal plane of the twin during the sliding of the disconnection. It is also predicted that a twin nucleates when the local gradient of elastic-energy or the average elastic-energy difference along the prismatic/basal boundary exhibit a sharp increase. Furthermore, the critical strain for twin nucleation can be obtained with the aid of local energy-based descriptors, when viewing twin nucleation as an instability phenomenon. Simulations suggest that both the local gradient and spatial average of elastic-energy difference are fundamental quantities behind the onset of twin nucleation at the prismatic/basal grain boundary in hexagonal close-packed metals under uniaxial loadings. Furthermore, results from our simulations and mechanics model, provide the position and the critical strain of the {10} twin nucleation at the prismatic/basal boundary. read less USED (high confidence) C. Race, “Atomistic simulations of grain boundary migration under recrystallisation conditions,” Modelling and Simulation in Materials Science and Engineering. 2019. link Times cited: 4 Abstract: We present details of an approach to simulating the migratio… read moreAbstract: We present details of an approach to simulating the migration of grain boundaries using classical molecular dynamics (MD) in a regime in which the boundary motion is driven by the presence of dislocation defects resulting from plastic deformation. By simulating the shrinkage of spherical grains of deformed material embedded in a perfect crystal, we create conditions in which grain boundary motion takes place on time scales accessible to MD simulations, in which the defect free energy acts as a driving force additional to the capillary force due to excess grain boundary energy. This approach is particularly flexible in allowing arbitrary choices of misorientation axis and angle and providing an interface in which all grain boundary plane orientations are represented. This flexibility is at the cost of additional complexity in the system under study and we establish an approach suitable for analysing the excess grain boundary energy and the components of the force for boundary motion on a local basis over the surface of the shrinking grain. We demonstrate that this approach is able to resolve variation in the grain boundary energy related to the intrinsic grain boundary dislocation network in lower angle boundaries and to detect local maxima in the driving force due to the dislocation structure within the deformed grain. We show that the variation in measured grain boundary velocities is accounted for by the excess energy of the dislocations. We further show that the presence of dislocations in the shrinking grain has a tendency to reduce the anisotropy in grain boundary behaviour. Indicative evidence is presented that the dislocation network may act as a focal point for mechanisms of grain boundary migration. read less USED (high confidence) H. Wang et al., “Dynamic recrystallization initiated by direct grain reorientation at high-angle grain boundary in α-titanium,” Journal of Materials Research. 2019. link Times cited: 3 Abstract: Employing atomic-scale simulations, the response of a high-a… read moreAbstract: Employing atomic-scale simulations, the response of a high-angle grain boundary (GB), the soft/hard GB, against external loading was systematically investigated. Under tensile loading close to the hard orientation, strain-induced dynamic recrystallization was observed to initiate through direct soft-to-hard grain reorientation, which was triggered by stress mismatch, inhibited by surface tension from the soft-hard GB, and proceeded by interface ledges. Such grain reorientation corresponds with expansion and contraction of the hard grain along and perpendicular to the loading direction, respectively, accompanied by local atomic shuffling, providing relatively large normal strain of 8.3% with activation energy of 0.04 eV per atom. Tensile strain and residual dislocations on the hard/soft GB facilitate the initiation of dynamic recrystallization by lowering the energy barrier and the critical stress for grain reorientation, respectively. read less USED (high confidence) X. Fan, Z. Rui, H. Cao, R. Fu, R. Feng, and C. Yan, “Nanoindentation of γ-TiAl with Different Crystal Surfaces by Molecular Dynamics Simulations,” Materials. 2019. link Times cited: 16 Abstract: The periodicity and density of atomic arrangement vary with … read moreAbstract: The periodicity and density of atomic arrangement vary with the crystal orientation, which results in different deformation mechanisms and mechanical properties of γ-TiAl. In this paper, the anisotropic characteristics for γ-TiAl with (100), ( 1 ¯ 10 ) and (111) surfaces during nanoindentation at 300 K have been investigated by molecular dynamics simulations. It is found that there is no obvious pop-in event in all load-depth curves when the initial plastic deformation of γ-TiAl samples occurs, because the dislocation nucleates before the first load-drop; while a peak appears in both the unloading curves of the ( 1 ¯ 10 ) and (111) samples due to the release of energy. Stacking faults, twin boundaries and vacancies are formed in all samples; however, interstitials are formed in the (100) sample, a stacking fault tetrahedron is formed in the (111) sample; and two prismatic dislocation loops with different activities are formed in the ( 1 ¯ 10 ) and (111) samples, respectively. It is also concluded that the values of the critical load, strain energy, hardness and elastic modulus for the (111) sample are the maximum, and for the (100) sample are the minimum. Furthermore, the orientation dependence of the elastic modulus is greater than the hardness and critical load. read less USED (high confidence) H. Cao, Z. Rui, W. Chen, R. Feng, and C. Yan, “Crack propagation mechanism of γ-TiAl alloy with pre-existing twin boundary,” Science China Technological Sciences. 2019. link Times cited: 12 USED (high confidence) H. Cao, Z. Rui, W. Chen, R. Feng, and C. Yan, “Crack propagation mechanism of γ-TiAl alloy with pre-existing twin boundary,” Science China Technological Sciences. 2019. link Times cited: 0 USED (high confidence) R. Feng, M. Wang, H. Li, Y. Qi, Q. Wang, and Z. Rui, “Micromechanism of Cold Deformation of Two-Phase Polycrystalline Ti–Al Alloy with Void,” Materials. 2019. link Times cited: 7 Abstract: Cold deformation behavior of polycrystalline metallic materi… read moreAbstract: Cold deformation behavior of polycrystalline metallic material is affected by intrinsic defects such as dislocations, voids, inclusions etc. Existing studies on α2(Ti3Al) + γ(TiAl) two-phase Ti–Al alloy cover about deformation behavior mainly on macro scale. This paper focuses on the cold deformation mechanism of two-phase Ti–Al alloy at micro scale, and the role of voids in deformation process. Molecular dynamics simulations were performed to study the evolution of micro structure of material under uniaxial tension. Interaction between spherical nano voids with different size and position was also examined in the simulation. The results show that (1) In elastic stage, deformation of the two-phase is coordinated, but Ti3Al is more deformable; (2) In plastic stage, γ phase is the major dislocation source in two-phase alloy; (3) voids detracts the strength of the two-phase alloy, while the position of void affect the degree of this subtraction, voids located at the boundary of α2/γ phase have significant detraction to strength. read less USED (high confidence) B. Syed et al., “Effect of work function and cohesive energy of the constituent phases of Ti-50 at.% Al cathode during arc deposition of Ti-Al-N coatings,” Surface and Coatings Technology. 2019. link Times cited: 8 USED (high confidence) S. Kiselev, “Numerical Molecular Dynamics Simulation of the Fracture of a Ti–Al Intermetallic Nanocrystal,” Doklady Physics. 2018. link Times cited: 0 USED (high confidence) L. Huber, R. Hadian, B. Grabowski, and J. Neugebauer, “A machine learning approach to model solute grain boundary segregation,” npj Computational Materials. 2018. link Times cited: 83 USED (high confidence) S. Kiselev et al., “Creating a Coating from a Titanium–Aluminum Intermetallic Compound By the Cold Spray Technology,” Journal of Applied Mechanics and Technical Physics. 2018. link Times cited: 0 USED (high confidence) S. Kiselev et al., “Creating a Coating from a Titanium–Aluminum Intermetallic Compound By the Cold Spray Technology,” Journal of Applied Mechanics and Technical Physics. 2018. link Times cited: 5 USED (high confidence) C. Hui, R. Zhiyuan, C. Wenke, F. Ruicheng, and Y. Changfeng, “Deformation mechanisms in nanotwinned γ-TiAl by molecular dynamics simulation,” Molecular Simulation. 2018. link Times cited: 14 Abstract: ABSTRACT In this work, the plastic deformation mechanisms an… read moreAbstract: ABSTRACT In this work, the plastic deformation mechanisms and fracture toughness of nanotwinned γ-TiAl with different twin boundary (TB) spacing are investigated by using molecular dynamics simulation. The simulation results reveal that there are pronounced shifts in the mechanical behaviour of nanotwinned γ-TiAl when the TB spacing is 3.50, 4.20 and 4.90 nm. In addition, the variation of the dislocation density with strain at these three TB spacing illustrates that a smaller TB spacing induces a higher dislocation density. Different TB spacing has an influence on the dislocation behaviour. The dislocation pile-up, dislocation–dislocation, dislocation–twin and twin–twin reactions, hierarchical twins including their generation and density, step formation, dislocation emission from steps and TB migration are the main plastic deformation mechanisms. The results also show that TB migration, twinning formation and interaction of crack and TB dominate the deformation mechanism of nanotwinned γ-TiAl with crack. The generation of hierarchical twins, lower distance between crack surface plane and twin plane, dislocation–twin, twin–twin interaction and crack deflection increase the fracture toughness of nanotwinned γ-TiAl. read less USED (high confidence) P. N. Mayer and A. Mayer, “Evolution of foamed aluminum melt at high rate tension: A mechanical model based on atomistic simulations,” Journal of Applied Physics. 2018. link Times cited: 13 Abstract: Dynamics of foamed metal melt relates to the following probl… read moreAbstract: Dynamics of foamed metal melt relates to the following problems: cavitations in melt at negative pressure; ablation and nanostructuring of the surface layer of materials under the action of powerful sub picosecond laser pulses; additive manufacturing; and production of solid foamed metals. We propose a mechanical model of the foamed melt evolution at the stage of bubble enlargement—after the completion of their nucleation and before the breaking of the inter-bubble walls. The foamed melt is considered as a system of strongly connected bubbles; their size variations are driven by surface forces. The interconnected system of equations for the second time derivatives of the bubble radii is derived by using the Lagrange formalism. The model is verified by comparison with the molecular dynamic (MD) simulation data for aluminum melt at high-rate uniform tension. An algorithm for searching of individual pores is developed and used to analyze the MD data. The size distribution of pores in the melt at the considered stage of enlargement is found to be close to the normal distribution on a finite interval. Evolution of the foamed melt structure is completely determined by the surface tension. The surface tension makes the largest bubbles growing and all the smaller bubbles collapsing, which leads to rapid reduction of the total number of bubbles. The foamed melt maintains negative pressure determined only by the size distribution of bubbles and the surface tension coefficient.Dynamics of foamed metal melt relates to the following problems: cavitations in melt at negative pressure; ablation and nanostructuring of the surface layer of materials under the action of powerful sub picosecond laser pulses; additive manufacturing; and production of solid foamed metals. We propose a mechanical model of the foamed melt evolution at the stage of bubble enlargement—after the completion of their nucleation and before the breaking of the inter-bubble walls. The foamed melt is considered as a system of strongly connected bubbles; their size variations are driven by surface forces. The interconnected system of equations for the second time derivatives of the bubble radii is derived by using the Lagrange formalism. The model is verified by comparison with the molecular dynamic (MD) simulation data for aluminum melt at high-rate uniform tension. An algorithm for searching of individual pores is developed and used to analyze the MD data. The size distribution of pores in the melt at the consider... read less USED (high confidence) E. Dolgusheva and V. Trubitsin, “Lattice Heat Capacity of Nanostructured Materials Based on Titanium/Zirconium and Aluminum,” Physics of the Solid State. 2018. link Times cited: 2 USED (high confidence) F. Rahmani, J. Jeon, S. Jiang, and S. Nouranian, “Melting and solidification behavior of Cu/Al and Ti/Al bimetallic core/shell nanoparticles during additive manufacturing by molecular dynamics simulation,” Journal of Nanoparticle Research. 2018. link Times cited: 28 USED (high confidence) D. Chanbi, E. Ogam, S. Amara, and Z. Fellah, “Synthesis and Mechanical Characterization of Binary and Ternary Intermetallic Alloys Based on Fe-Ti-Al by Resonant Ultrasound Vibrational Methods,” Materials. 2018. link Times cited: 11 Abstract: Precise but simple experimental and inverse methods allowing… read moreAbstract: Precise but simple experimental and inverse methods allowing the recovery of mechanical material parameters are necessary for the exploration of materials with novel crystallographic structures and elastic properties, particularly for new materials and those existing only in theory. The alloys studied herein are of new atomic compositions. This paper reports an experimental study involving the synthesis and development of methods for the determination of the elastic properties of binary (Fe-Al, Fe-Ti and Ti-Al) and ternary (Fe-Ti-Al) intermetallic alloys with different concentrations of their individual constituents. The alloys studied were synthesized from high purity metals using an arc furnace with argon flow to ensure their uniformity and homogeneity. Precise but simple methods for the recovery of the elastic constants of the isotropic metals from resonant ultrasound vibration data were developed. These methods allowed the fine analysis of the relationships between the atomic concentration of a given constituent and the Young’s modulus or alloy density. read less USED (high confidence) R. Hadian, B. Grabowski, M. Finnis, and J. Neugebauer, “Migration mechanisms of a faceted grain boundary,” Physical Review Materials. 2018. link Times cited: 19 Abstract: We report molecular dynamics simulations and their analysis … read moreAbstract: We report molecular dynamics simulations and their analysis for a mixed tilt and twist grain boundary vicinal to the $\mathrm{\ensuremath{\Sigma}}7$ symmetric tilt boundary of the type ${1\phantom{\rule{0.16em}{0ex}}2\phantom{\rule{0.16em}{0ex}}3}$ in aluminum. When minimized in energy at $0\phantom{\rule{0.16em}{0ex}}\mathrm{K}$, a grain boundary of this type exhibits nanofacets that contain kinks. We observe that at higher temperatures of migration simulations, given extended annealing times, it is energetically favorable for these nanofacets to coalesce into a large terrace-facet structure. Therefore, we initiate the simulations from such a structure and study as a function of applied driving force and temperature how the boundary migrates. We find the migration of a faceted boundary can be described in terms of the flow of steps. The migration is dominated at lower driving force by the collective motion of the steps incorporated in the facet, and at higher driving forces by the step detachment from the terrace-facet junction and propagation of steps across the terraces. The velocity of steps on terraces is faster than their velocity when incorporated in the facet, and very much faster than the velocity of the facet profile itself, which is almost stationary. A simple kinetic Monte Carlo model matches the broad kinematic features revealed by the molecular dynamics. Since the mechanisms seem likely to be very general on kinked grain-boundary planes, the step-flow description is a promising approach to more quantitative modeling of general grain boundaries. read less USED (high confidence) H. Men and Z. Fan, “Prenucleation Induced by Crystalline Substrates,” Metallurgical and Materials Transactions A. 2018. link Times cited: 38 USED (high confidence) C. Li et al., “Physical characteristics of nanoscale niobium-zirconium alloy powder during 3D printing laser sintering process — A molecular dynamics study,” 2018 IEEE International Conference on Applied System Invention (ICASI). 2018. link Times cited: 3 Abstract: In this present study, the physical characteristics of nanos… read moreAbstract: In this present study, the physical characteristics of nanoscale niobium zirconium alloy powder applied on the powder bed fusion laser sintering is computed during 3D printing process by molecular dynamics simulation method with embedded atom method potential. There are three solid and hollow type powder sizes, which are 16a, 20a, and 24a, respectively. There are three solid and hollow type powder sizes, which are 16a, 20a, and 24a, respectively. Six combinations are created and laser-sintered under different heating rates (1K/ps, 0.5K/ps, and 0.25K/ps, respectively), and then the neck width, radius of gyration, structural change, potential energy, and root mean square displacement of nanoscale alloy powder are analyzed and discussed. It is found that nanoscale niobium zirconium alloy powder has the phenomena of spontaneous solid-state sintering at room temperature. It is observed that the temperature of solid state diffusion decrease with heating rate decreasing when powder size fixed, the temperature of solid state diffusion decrease with powder size decreasing when heating rate fixed also. Average coalescence temperature and melting temperature decrease with heating rate decreasing when powder size fixed, and they decrease with powder size decreasing when heating rate fixed also. It is mentioned that coalescence temperature of nanoscale niobium zirconium alloy powder is about 1250 to 1800K, and melting temperature of that is about 1250 to 1800K (The macroscopic melting of that point is 2070 K). Therefore, it is suggested that the power of laser beams could be lower during 3D printing process in order to heat nanoscale niobium zirconium alloy powder. read less USED (high confidence) S. Sun, B. Ramachandran, and C. Wick, “Solid, liquid, and interfacial properties of TiAl alloys: parameterization of a new modified embedded atom method model,” Journal of Physics: Condensed Matter. 2018. link Times cited: 11 Abstract: New interatomic potentials for pure Ti and Al, and binary Ti… read moreAbstract: New interatomic potentials for pure Ti and Al, and binary TiAl were developed utilizing the second nearest neighbour modified embedded-atom method (MEAM) formalism. The potentials were parameterized to reproduce multiple properties spanning bulk solids, solid surfaces, solid/liquid phase changes, and liquid interfacial properties. This was carried out using a newly developed optimization procedure that combined the simple minimization of a fitness function with a genetic algorithm to efficiently span the parameter space. The resulting MEAM potentials gave good agreement with experimental and DFT solid and liquid properties, and reproduced the melting points for Ti, Al, and TiAl. However, the surface tensions from the model consistently underestimated experimental values. Liquid TiAl’s surface was found to be mostly covered with Al atoms, showing that Al has a significant propensity for the liquid/air interface. read less USED (high confidence) P. Li et al., “Molecular dynamic simulation of nanocrystal formation and tensile deformation of TiAl alloy,” RSC Advances. 2017. link Times cited: 15 Abstract: The formation of nanocrystals from undercooling TiAl melt an… read moreAbstract: The formation of nanocrystals from undercooling TiAl melt and deformation behavior of nanocrystalline TiAl alloy under tensile loading conditions are investigated by molecular dynamics simulation. The effects of quenching rate related to the solidification structure evolution during rapid quenching are described by internal energy, radial distribution functions, and common neighbor analysis. The simulation results indicate that the accumulation of atoms with icosahedral configuration and transformation into atomic cluster with BCC configuration in the undercooling melt are the key in crystalline nucleation growth, and eventually liquid TiAl alloy completely crystallizes at the quenching rate of 0.02 K ps−1. In the tensile deformation, grain boundaries sliding and lamellar domain increasing are the two main deformation mechanisms during plastic deformation, and cracks form due to the nucleation, growth and coalescence of void along the grain boundaries, which results in subsequent failure in nanocrystalline TiAl alloy. This paper provides fundamental understanding of the nanocrystalline formation of undercooling TiAl melt and the deformation mechanisms in the nanocrystalline TiAl at the atomic scale. read less USED (high confidence) M. Kanani, A. Hartmaier, and R. Janisch, “The shear instability energy: a new parameter for materials design?,” Modelling and Simulation in Materials Science and Engineering. 2017. link Times cited: 1 Abstract: Reliable and predictive relationships between fundamental mi… read moreAbstract: Reliable and predictive relationships between fundamental microstructural material properties and observable macroscopic mechanical behaviour are needed for the successful design of new materials. In this study we establish a link between physical properties that are defined on the atomic level and the deformation mechanisms of slip planes and interfaces that govern the mechanical behaviour of a metallic material. To accomplish this, the shear instability energy Γ is introduced, which can be determined via quantum mechanical ab initio calculations or other atomistic methods. The concept is based on a multilayer generalised stacking fault energy calculation and can be applied to distinguish the different shear deformation mechanisms occurring at TiAl interfaces during finite-temperature molecular dynamics simulations. We use the new parameter Γ to construct a deformation mechanism map for different interfaces occurring in this intermetallic. Furthermore, Γ can be used to convert the results of ab initio density functional theory calculations into those obtained with an embedded atom method type potential for TiAl. We propose to include this new physical parameter into material databases to apply it for the design of materials and microstructures, which so far mainly relies on single-crystal values for the unstable and stable stacking fault energy. read less USED (high confidence) S. Kiselev and V. Kiselev, “Numerical simulation of titanium dissolution in the aluminum melt and synthesis of an intermetallic compound,” Journal of Applied Mechanics and Technical Physics. 2017. link Times cited: 1 USED (high confidence) Y. Liu, Y.-chun Huang, Z. Xiao, and G. Jia, “First Principles Study of Adsorption of Hydrogen on Typical Alloying Elements and Inclusions in Molten 2219 Al Alloy,” Materials. 2017. link Times cited: 3 Abstract: To better understand the effect of the components of molten … read moreAbstract: To better understand the effect of the components of molten 2219 Al alloy on the hydrogen content dissolved in it, the H adsorption on various positions of alloying element clusters of Cu, Mn and Al, as well as the inclusion of Al2O3, MgO and Al4C3, were investigated by means of first principles calculation, and the thermodynamic stability of H adsorbed on each possible site was also studied on the basis of formation energy. Results show that the interaction between Al, MgO, Al4C3 and H atoms is mainly repulsive and energetically unfavorable; a favorable interaction between Cu, Mn, Al2O3 and H atoms was determined, with H being more likely to be adsorbed on the top of the third atomic layer of Cu(111), the second atomic layer of Mn(111), and the O atom in the third atomic layer of Al2O3, compared with other sites. It was found that alloying elements Cu and Mn and including Al2O3 may increase the hydrogen adsorption in the molten 2219 Al alloy with Al2O3 being the most sensitive component in this regard. read less USED (high confidence) Z. Wu, X. Yang, and Z. Wang, “Size effect on the spontaneous coalescence of nanowires,” Nanotechnology. 2017. link Times cited: 8 Abstract: This paper investigates the size effect on the coalescence p… read moreAbstract: This paper investigates the size effect on the coalescence process of contacting nanoparticles. It is revealed by molecular dynamics that the nanometer-sized surface curvature coupled with the effective melting temperature exhibits a strong influence on the atom diffusion at the interface, and is therefore critical to the coalescence time. This effect is particularly pronouncing for surface curvatures below 20 nm. A phenomenological model is derived from the melting point reduction approach to describe the kinetic process of nanowire coalescence and is validated against a variety of simulation datasets. The quantitative correlation between the sample size, the sintering temperature and the contact morphology evolution is demonstrated. read less USED (high confidence) D. Luo, Z. Rui, H. Cao, and R. Fu, “The Energy Spectrum Fluctuation Size Effect Study of the Holes in the Crystal - TiAl Crack Propagation,” DEStech Transactions on Materials Science and Engineering. 2017. link Times cited: 0 Abstract: The paper studied the sized effect for the system energy spe… read moreAbstract: The paper studied the sized effect for the system energy spectrum wave phenomenon in the process of crack propagation for the single crystal gamma - TiAl alloy of the hole defects. With the ways of molecular dynamics method and used the embedded atom potential method, The different hole size ( R=1A 、2A 、 3A ) influenced the system energy change (curve a, b, c)in the process of the crack propagations combined with atomic path chart were analysised. The results indicated that the three energy evolution curve models showed the fluctuating phenomenons; Three curves had the same change trend before t = 125 ps, the total energy showed a trend of increased with the Internal atomic fuel movement , and the kinetic energy and potential energy increased. With load continued, The curve a, b, c appeared the low energy at t = 172 ps, t = 188 ps, t = 186 ps respectively, and the energy values is 648483.4 E/ev, 647674.85 E/ev, 646124.39 E/ev respectively; The hole effect model of the different holes size R=1A 、 3A appeared The main and second cracks convergence phenomenon at t = 560Ps, t = 732 ps respectively, and the energy attained secondary low value 648671.12 E/ev, 645719.59 E/ev respectively; On the whole, the curve c is stable relatively, the fluctuation amplitude was small, and the overall energy was the minimum, and the curve a and b fluctuations was bigger. read less USED (high confidence) A. Ready, P. Haynes, D. Rugg, and A. Sutton, “Stacking faults and the -surface on first-order pyramidal planes in -titanium,” Philosophical Magazine. 2017. link Times cited: 6 Abstract: Using first principles methods, we calculated the entire -su… read moreAbstract: Using first principles methods, we calculated the entire -surface of the first-order pyramidal planes in -titanium. Slip on these planes involving dislocations with -type Burgers vectors is one means by which -titanium polycrystals may supplement slip on prism planes with -type Burgers vectors to maintain ductility. We find one low energy and one high energy stacking fault with energies of 163 and 681 , respectively. Contrary to previous suggestions, we do not find a stable stable stacking fault at . read less USED (high confidence) A. Venkataraman et al., “Study of Structure and Deformation Pathways in Ti-7Al Using Atomistic Simulations, Experiments, and Characterization,” Metallurgical and Materials Transactions A. 2017. link Times cited: 22 USED (high confidence) A. Zinovev, M. G. Bapanina, R. Babicheva, N. Enikeev, S. Dmitriev, and K. Zhou, “Deformation of nanocrystalline binary aluminum alloys with segregation of Mg, Co and Ti at grain boundaries,” Physics of Metals and Metallography. 2017. link Times cited: 6 USED (high confidence) Y. Liu, Y.-chun Huang, Z. Xiao, and X. Reng, “Study of Adsorption of Hydrogen on Al, Cu, Mg, Ti Surfaces in Al Alloy Melt via First Principles Calculation.” 2017. link Times cited: 20 Abstract: Adsorption of hydrogen on Al(111), Cu(111), Mg(0001), and Ti… read moreAbstract: Adsorption of hydrogen on Al(111), Cu(111), Mg(0001), and Ti(0001) surfaces have been investigated by means of first principles calculation. The calculation of surface energy indicates that Mg(0001) is the most stable surface, while Ti(0001) is the most unstable surface among all the four calculated surfaces. The obtained adsorption energy shows that the interaction between Al and H atoms should be energetically unfavorable, and the adsorption of hydrogen on Mg(0001) surface was found to be energetically preferred. Besides, the stability of hydrogen adsorption on studied surfaces increased in the order of Al(111), Ti(0001), Cu(111), Mg(0001). Calculation results also reveal that hydrogen adsorption on fcc and hcp sites are energetically stable compared with top and bridge sites for Ti(0001), Cu(111), and Mg(0001), while hydrogen adsorbing at the top site of Al(111) is the most unstable state compared with other sites. The calculated results agreed well with results from experiments and values in other calculations. read less USED (high confidence) J. Gu, Y. Shen, X. Liu, and J. Li, “Crystal metamorphosis at stress extremes: how soft phonons turn into lattice defects,” Nature. 2016. link Times cited: 8 USED (high confidence) P. N. Mayer and A. Mayer, “Late stages of high rate tension of aluminum melt: Molecular dynamic simulation,” Journal of Applied Physics. 2016. link Times cited: 30 Abstract: With the help of molecular dynamic simulation, we investigat… read moreAbstract: With the help of molecular dynamic simulation, we investigate late stages of aluminum melt tension up to the deformation degree of about 10, including a stage of bubble liquid, a foamed melt, and a fragmentation with formation of droplets. Complete fracture of melt is a complex process, which includes nucleation of pores, growth and coalescence of neighboring pores, thinning and breaking of walls between them with the formation of a system of jets, and, finally, breaking of jets into droplets. The transition from the foamed melt to the system of jets and the subsequent fragmentation into droplets occur at the volume fraction of condensed matter considerably smaller than 0.1. The number of pores at the volume fraction of condensed matter about 0.5 and the number of droplets at the final stage of fragmentation are not directly connected with each other. At the same time, both numbers are increased together with the increase in the strain rate and have the same order of magnitude. At the stage of melt with pores, the growth and coalescence of pores are controlled by surface tension, which allows us to construct an analytical estimation for time dependence of the pore average radius. Also, we propose analytical estimations for the mean pressure of melt with pores, which remain negative, and for the work of tension. A few times larger work is spent on the tension of melt with pores if compared with the initial stage of tension near the dynamic strength threshold. The last fact is favorable for the production of the foamed aluminum by means of the high-rate tension of its melt. read less USED (high confidence) P. Li, Y.-qing Yang, W. Zhang, X. Luo, N. Jin, and G. Liu, “Structural evolution of TiAl during rapid solidification processing revealed by molecular dynamics simulations,” RSC Advances. 2016. link Times cited: 12 Abstract: In this paper, the processes of rapid solidification in TiAl… read moreAbstract: In this paper, the processes of rapid solidification in TiAl was investigated by molecular dynamics simulations. The structure transformation which occurs during solidification is described by internal energy, radial distribution functions, Honeycutt-Anderson pair analysis technique, mean square displacement and simulation of powder X-ray diffraction patterns. The effects of different cooling rates, 50–0.005 K ps−1, on the amorphous structure formation and crystallization of liquid TiAl are simulated. The results show that an amorphous phase can be obtained when the cooling rate is not less than 0.02 K ps−1, and γ-TiAl + α2-Ti3Al mixed phases can be formed when the cooling rate is 0.01 K ps−1. read less USED (high confidence) R. Babicheva et al., “Elastic moduli of nanocrystalline binary Al alloys with Fe, Co, Ti, Mg and Pb alloying elements,” Philosophical Magazine. 2016. link Times cited: 13 Abstract: The paper studies the elastic moduli of nanocrystalline (NC)… read moreAbstract: The paper studies the elastic moduli of nanocrystalline (NC) Al and NC binary Al–X alloys (X is Fe, Co, Ti, Mg or Pb) by using molecular dynamics simulations. X atoms in the alloys are either segregated to grain boundaries (GBs) or distributed randomly as in disordered solid solution. At 0 K, the rigidity of the alloys increases with decrease in atomic radii of the alloying elements. An addition of Fe, Co or Ti to the NC Al leads to increase in the Young’s E and shear μ moduli, while an alloying with Pb decreases them. The elastic moduli of the alloys depend on a distribution of the alloying elements. The alloys with the random distribution of Fe or Ti demonstrate larger E and μ than those for the corresponding alloys with GB segregations, while the rigidity of the Al–Co alloy is higher for the case of the GB segregations. The moduli E and μ for polycrystalline aggregates of Al and Al–X alloys with randomly distributed X atoms are estimated based on the elastic constants of corresponding single-crystals according to the Voigt-Reuss-Hill approximation, which neglects the contribution of GBs to the rigidity. The results show that GBs in NC materials noticeably reduce their rigidity. Furthermore, the temperature dependence of μ for the NC Al–X alloys is analyzed. Only the Al–Co alloy with GB segregations shows the decrease in μ to the lowest extent in the temperature range of 0–600 K in comparison with the NC pure Al. read less USED (high confidence) S. Kiselev, “Modeling the crystallization of a Ti–Al nanoparticle by the molecular dynamics method,” Doklady Physics. 2016. link Times cited: 7 USED (high confidence) Z. Jinping, Y. Zhang, W. Erping, C. Tang, X. Cheng, and Q. Zhang, “Size effect in the melting and freezing behaviors of Al/Ti core-shell nanoparticles using molecular dynamics simulations*,” Chinese Physics B. 2016. link Times cited: 8 Abstract: The thermal stability of Ti@Al core/shell nanoparticles with… read moreAbstract: The thermal stability of Ti@Al core/shell nanoparticles with different sizes and components during continuous heating and cooling processes is examined by a molecular dynamics simulation with embedded atom method. The thermodynamic properties and structure evolution during continuous heating and cooling processes are investigated through the characterization of the potential energy, specific heat distribution, and radial distribution function (RDF). Our study shows that, for fixed Ti core size, the melting temperature decreases with Al shell thickness, while the crystallizing temperature and glass formation temperature increase with Al shell thickness. Diverse melting mechanisms have been discovered for different Ti core sized with fixed Al shell thickness nanoparticles. The melting temperature increases with the Ti core radius. The trend agrees well with the theoretical phase diagram of bimetallic nanoparticles. In addition, the glass phase formation of Al–Ti nanoparticles for the fast cooling rate of 12 K/ps, and the crystal phase formation for the low cooling rate of 0.15 K/ps. The icosahedron structure is formed in the frozen 4366 Al–Ti atoms for the low cooling rate. read less USED (high confidence) B. Li, “Shear and shuffle in
\left{11\bar 22 \right}\left⟨11\bar 2\bar 3 \right⟩twinning in titanium,” Journal of Materials Research. 2015. link Times cited: 3 Abstract: In classical twinning theory, the K _2 plane of $\left\{{11\… read moreAbstract: In classical twinning theory, the K _2 plane of $\left\{{11\bar 22} \right\}\left\langle {11\bar 2\bar 3} \right\rangle$ twinning mode was predicted to be $\left\{{11\bar 2\bar 4} \right\}$ , with a twinning shear of ∼0.22 which was experimentally “confirmed”. However, these twinning elements cannot be reproduced or verified in atomistic simulations. The K _2 plane in the simulations is always (0001), but this K _2 plane would lead to a nominal twining shear of 1.26 which is unrealistically large. In this work, atomistic simulations were performed to investigate the migration of $\left\{{11\bar 22} \right\}$ twin boundary in titanium (Ti). Shear and atomic shuffles for three different, reported K _2 planes were analyzed in great detail, for the first time. The analyses show that ${K_2} = \left\{{11\bar 2\bar 4} \right\}$ leads to very complex shuffles despite the small twinning shear and is unfavorable. If ${K_2} = \left\{{11\bar 2\bar 2} \right\}$ , only half of the parent atoms are involved in the shuffling, but the twinning shear is very large (0.96) and is also unfavorable. When K _2 = (0001), the parent atoms are carried to twin positions partly by shear and partly by a simple shuffle. Because shuffling makes no contribution to the twinning shear, the actual twinning shear is 0.66, instead of 1.26. Thus, K _2 = (0001) is the most favorable and the conflict between the simulation results and the classical twinning theory can be reconciled. read less USED (high confidence) W. Guo, Z. Wang, and J. Li, “Diffusive versus Displacive Contact Plasticity of Nanoscale Asperities: Temperature- and Velocity-Dependent Strongest Size.,” Nano letters. 2015. link Times cited: 32 Abstract: We predict a strongest size for the contact strength when as… read moreAbstract: We predict a strongest size for the contact strength when asperity radii of curvature decrease below 10 nm. The reason for such strongest size is found to be correlated with the competition between the dislocation plasticity and surface diffusional plasticity. The essential role of temperature is calculated and illustrated in a comprehensive asperity size-strength-temperature map taking into account the effect of contact velocity. Such a map should be essential for various phenomena related to nanoscale contacts such as nanowire cold welding, self-assembly of nanoparticles and adhesive nanopillar arrays, as well as the electrical, thermal, and mechanical properties of macroscopic interfaces. read less USED (high confidence) C. Race, “Quantifying uncertainty in molecular dynamics simulations of grain boundary migration,” Molecular Simulation. 2015. link Times cited: 17 Abstract: Molecular dynamics simulations of simple bicrystal systems h… read moreAbstract: Molecular dynamics simulations of simple bicrystal systems have been much used as a tool to explore how the migration of grain boundaries varies with their structure and with experimental conditions. In order to permit the exploration of a large parameter space, many studies are forced to rely on a small number of simulations (often a single simulation) for each configuration. The motion of a grain boundary is inherently statistical and any variability in the measured grain boundary velocity should be taken into account in subsequent analysis of trends in grain boundary mobility. Here we present the results of large numbers of simulations of equivalent boundaries, which show that this variability can be large, particularly when small systems are simulated. We show how a bootstrap resampling approach can be used to characterise the statistical uncertainty in boundary velocity using the information present in a single simulation. We show that the approach is robust across a variety of system sizes, temperatures and driving force strengths and types, and provides a good order-of-magnitude measure of the population standard deviation across multiple equivalent simulations. read less USED (high confidence) A. Mayer and P. N. Mayer, “Continuum model of tensile fracture of metal melts and its application to a problem of high-current electron irradiation of metals,” Journal of Applied Physics. 2015. link Times cited: 36 Abstract: A continuum model of the metal melt fracture is formulated o… read moreAbstract: A continuum model of the metal melt fracture is formulated on the basis of the continuum mechanics and theory of metastable liquid. A character of temperature and strain rate dependences of the tensile strength that is predicted by the continuum model is verified, and parameters of the model are fitted with the use of the results of the molecular dynamics simulations for ultra-high strain rates (≥1–10/ns). A comparison with experimental data from literature is also presented for Al and Ni melts. Using the continuum model, the dynamic tensile strength of initially uniform melts of Al, Cu, Ni, Fe, Ti, and Pb within a wide range of strain rates (from 1–10/ms to 100/ns) and temperatures (from melting temperature up to 70–80% of critical temperature) is calculated. The model is applied to numerical investigation of a problem of the high-current electron irradiation of Al, Cu, and Fe targets. read less USED (high confidence) L. Zhang 张, Lü 程 Cheng 吕, T. Kiet, X. Zhao 赵, Lin-Qing 林清 Pei 裴, and M. Guillaume, “Molecular dynamics simulation on generalized stacking fault energies of FCC metals under preloading stress,” Chinese Physics B. 2015. link Times cited: 18 Abstract: Molecular dynamics (MD) simulations are performed to investi… read moreAbstract: Molecular dynamics (MD) simulations are performed to investigate the effects of stress on generalized stacking fault (GSF) energy of three fcc metals (Cu, Al, and Ni). The simulation model is deformed by uniaxial tension or compression in each of [111], [11-2], and [1-10] directions, respectively, before shifting the lattice to calculate the GSF curve. Simulation results show that the values of unstable stacking fault energy (γusf), stable stacking fault energy (γsf), and unstable twin fault energy (γutf) of the three elements can change with the preloaded tensile or compressive stress in different directions. The ratio of γsf/γusf, which is related to the energy barrier for full dislocation nucleation, and the ratio of γutf/γusf, which is related to the energy barrier for twinning formation are plotted each as a function of the preloading stress. The results of this study reveal that the stress state can change the energy barrier of defect nucleation in the crystal lattice, and thereby can play an important role in the deformation mechanism of nanocrystalline material. read less USED (high confidence) K. Xiong, X. Liu, and J. Gu, “Multiscale modeling of lattice dynamical instability in gamma-TiAl crystal,” Modelling and Simulation in Materials Science and Engineering. 2015. link Times cited: 5 Abstract: In this paper, the lattice instability of γ-TiAl crystal und… read moreAbstract: In this paper, the lattice instability of γ-TiAl crystal under different loading modes was studied using a lattice dynamical finite-element method (LDFEM) and molecular dynamics (MD). The simulation results show that the lattice instability of γ-TiAl crystal is significantly influenced by loading modes and crystallographic orientations. In uniaxial loading, γ-TiAl crystal exhibits tension-compression asymmetry in critical stress. The stress–strain curves and the active slip systems obtained from LDFEM simulations are in agreement with those in MD simulations. In the nanoindentation of γ-TiAl crystal, surface orientation plays an important role in stress field, lattice instability and dislocation nucleation. The LDFEM accurately predicts the location of lattice instability and the active slip systems. The surface effect on lattice instability in nanoindentation was also proved by performing a cylindrical nanoindentation. read less USED (high confidence) M. A. Bhatia, X. Zhang, M. Azarnoush, G. Lu, and K. Solanki, “Effects of oxygen on prismatic faults in α-Ti: a combined quantum mechanics/molecular mechanics study,” Scripta Materialia. 2015. link Times cited: 22 USED (high confidence) H. Wang, D. S. Xu, and R. Yang, “Atomic modelling of crack initiation on twin boundaries in α-titanium under external tensile loading along various orientations,” Philosophical Magazine Letters. 2014. link Times cited: 8 Abstract: Dislocation-grain boundary interaction is considered as the … read moreAbstract: Dislocation-grain boundary interaction is considered as the core issue of fatigue crack initiation in α-titanium alloys, where, however, the underlying processes still remain unclear. In the present study, the interaction between 〈a〉-dislocations and coherent twin boundaries is simulated with molecular dynamics under various tensile loading orientations. Plastic deformation is found to depend on the tensile orientation, and two typical processes are revealed. In the first, the dislocation transfers into the neighbour grain across the boundary, promoting deformation twinning followed by basal crack initiation, while in the second, the dislocation rebounded at the boundary, resulting in basal crack nucleation therein. In both cases, residual defect structures are left at the boundaries. These results indicate that there exist a wide range of loading orientations, under which dislocation-coherent twin boundary interaction promotes crack initiation on the basal plane; hence, implying its potential relevance to fracture faceting in α-titanium alloys. read less USED (high confidence) K. Xiong, X. Liu, and J. Gu, “Orientation-dependent crystal instability of gamma-TiAl in nanoindentation investigated by a multiscale interatomic potential finite-element model,” Modelling and Simulation in Materials Science and Engineering. 2014. link Times cited: 8 Abstract: The anisotropic mechanical behavior of γ-TiAl alloys has bee… read moreAbstract: The anisotropic mechanical behavior of γ-TiAl alloys has been observed and repeatedly reported, but the effect of crystallographic orientations on the crystal instability of γ-TiAl is still unclear. In this paper, the orientation-dependent crystal instability of γ-TiAl single crystals was investigated by performing nanoindentation on different crystal surfaces. All the nanoindentations are simulated using an interatomic potential finite-element model (IPFEM). Simulation results show that the load–displacement curves, critical indentation depth and critical load for crystal instability as well as indentation modulus, are all associated with surface orientations. The active slip systems and the location of crystal instability in five typical nanoindentations are analyzed in detail, i.e. the (0 0 1), (1 0 0), (1 0 1), (1 1 0) and (1 1 1) crystal surfaces. The predicted crystal instability sites and the activated slipping systems in the IPFEM simulations are in good agreement with the dislocation nucleation in molecular dynamics simulations. read less USED (high confidence) H. Sun and C. Deng, “Direct quantification of solute effects on grain boundary motion by atomistic simulations,” Computational Materials Science. 2014. link Times cited: 35 USED (high confidence) J.-Q. Ren, Q. Sun, L. Xiao, X. Ding, and J. Sun, “Phase transformation behavior in titanium single-crystal nanopillars under [0 0 0 1] orientation tension: A molecular dynamics simulation,” Computational Materials Science. 2014. link Times cited: 66 USED (high confidence) V. K. Sutrakar, “Atomistic modeling of strain-controlled cyclic loading in TiAl crystalline nanowire,” Journal of Physics: Condensed Matter. 2014. link Times cited: 3 Abstract: In this paper, atomistic modeling of L10–TiAl nanowire has b… read moreAbstract: In this paper, atomistic modeling of L10–TiAl nanowire has been performed utilizing the Embedded Atom Method (EAM) potential under strain-controlled cyclic loading. A nanowire oriented along the <100> axis with a cross-sectional dimension (D) of ~80 Å with a Length-to-width (L/D) ratio of 10.0 has been considered. Strain-controlled cyclic loading at room temperature has been performed by oscillating the nanowire length dimension sinusoidal with a specific amplitude and period. Tension-compression cyclic loading was employed with zero mean strain. Cyclic loading with percentage strains (%ε) of one to five percent have been considered. It has been observed that the cyclic stress in the nanowire continues to fluctuate during the initial loading cycles. However, once the nanowire becomes stable, a smooth variation of stresses with varying strain has been observed. The cause of initial fluctuations in the nanowire has been studied by varying (a) the amount of load (strain) applied, (b) the nanowire structure during cyclic loading, and (c) the rate at which the load has been applied. It has been identified that the rate of loading could be used for controlling the initial fluctuations of nanowire. Finally, a method for the calculation of cyclic stress versus cyclic strain for nanowires has been proposed. A cyclic stress versus cyclic strain curve has been plotted for a given L/D = 10 and a period of 10 ps. Results show that the TiAl nanowire is having 3/2 times higher stiffness in tension as compared to compression at a given strain under cyclic loading. read less USED (high confidence) N. Tarrat, M. Benoit, D. Caillard, L. Ventelon, N. Combe, and J. Morillo, “Screw dislocation in hcp Ti : DFT dislocation excess energies and metastable core structures,” Modelling and Simulation in Materials Science and Engineering. 2014. link Times cited: 27 Abstract: An extensive DFT search of (meta)stable structures of the sc… read moreAbstract: An extensive DFT search of (meta)stable structures of the screw dislocation in hcp-Ti is presented. It reveals that the stable core structures are never basal but always prismatic. This prismatic core dissociates into two partial dislocations in the same or neighboring prismatic planes depending on the initial position of the dislocation line, leading to either a symmetric or an asymmetric core. An alternative way of defining the core region from an electronic structure point of view is also proposed. It evidences clearly the symmetric or asymmetric character of the cores. We then introduce an ansatz for a straightforward and fast calculation of the excess energy, per unit length of dislocation, of a screw dislocation applicable to DFT calculations, in the cluster approach. The method is first validated on calculations of a screw dislocation in hcp-Ti, performed with an EAM potential from which exact excess energies can be extracted. Then, it is shown that it does work in a DFT calculation, through its application to the same screw dislocation in hcp-Ti with an accuracy of 8.4 meV/Å (1.8% of the excess energy for a cluster of 126 atoms per plane normal to the dislocation line). The comparison of the excess energies of the symmetric and assymmetric cores, calculated with the proposed ansatz, reveals that their energy difference is within the uncertainty of the method, which implies that the potential energy surface is very flat and that there could be many metastable core structures in hcp-Ti. read less USED (high confidence) X. Sang, A. Kulovits, G. Wang, and J. Wiezorek, “High precision electronic charge density determination for L10-ordered γ-TiAl by quantitative convergent beam electron diffraction,” Philosophical Magazine. 2012. link Times cited: 3 Abstract: Low order structure and Debye–Waller (DW) factors for tetrag… read moreAbstract: Low order structure and Debye–Waller (DW) factors for tetragonal L10-ordered γ-TiAl were measured simultaneously using quantitative convergent beam electron diffraction. The high precision and accuracy (largest error <0.5%) measurements allowed the construction of charge density difference maps from full sets of structure and DW factors, suitable for validation of first principles density functional theory (DFT) calculation results. Comparison of the experimentally determined charge density distribution with theoretical DFT predictions shows excellent qualitative agreement in this study. The three-dimensional charge density representations indicate a large electron charge localisation centred about the tetrahedral site at ¼, ¼, ¼, which is coordinated by two Ti atoms at 0, 0, 0 and ½, ½, 0 and two Al atoms at ½, 0, ½ and 0, ½, ½, respectively. Compared to experimental data, the DFT calculations based on full-potential linearised augmented plane wave (LAPW) method (implemented in WIEN2K) were found to quantitatively overestimate charge density between Ti–Ti second nearest neighbour atoms. Moreover, the results from the DFT method based on the projector-augmented wave (PAW) method and a plane wave basis set (implemented in VASP) were found to differ appreciably from both the experimental and LAPW-DFT results, implying that the PAW approach may not accurately describe the bonding in the intermetallic systems with 3 d electrons, such as γ-TiAl. read less USED (high confidence) L. Xiong and Y. Chen, “Coarse-Grained Atomistic Modeling and Simulation of Inelastic Material Behavior,” Acta Mechanica Solida Sinica. 2012. link Times cited: 8 USED (high confidence) J. Wang and I. Beyerlein, “Atomic Structures of $ [0\bar110] $ Symmetric Tilt Grain Boundaries in Hexagonal Close-Packed (hcp) Crystals,” Metallurgical and Materials Transactions A. 2012. link Times cited: 66 USED (high confidence) J. Chu and C. Steeves, “Thermal expansion and recrystallization of amorphous Al and Ti: A molecular dynamics study,” Journal of Non-crystalline Solids. 2011. link Times cited: 23 USED (high confidence) H. Choi, G. Yoon, and Y.-C. Chung, “Atomic-Scale Investigation on the Ti/Fe(001) Interface Structure: Molecular Dynamics Simulations and Ab initio Calculations,” Japanese Journal of Applied Physics. 2011. link Times cited: 0 Abstract: The structure dependent magnetism and intermixing characteri… read moreAbstract: The structure dependent magnetism and intermixing characteristics of Ti/Fe(001) thin films were investigated using molecular dynamics simulations and ab initio calculations. Through density functional theory based ab initio calculations, sharply decreased demagnetization energy of Fe(001) substrate by the interface intermixing was observed. The intermixing at the Ti/Fe(001) interface was limited within only the topmost layer of the Fe(001) substrate at temperatures ranging from 300 to 600 K with incident energies of a Ti atom from 0.1 to 5 eV. Both the high deposition temperature and the high incident energy of the Ti adatom inproved the surface smoothness of the deposited Ti films. The elevated temperature significantly increased the amount of Ti/Fe interface intermixing, while the incident energy dependency was negligible. The extremely low atomic intermixing ratio and short diffusion length of Ti/Fe system compared to other transition metal thin films could be explained by comparing the local acceleration and incorporation energy barrier effects. read less USED (high confidence) G. Yoon, S.-G. Lee, B.-H. Kim, and Y.-C. Chung, “Atomic-Scale Investigation of the Ti/Al(001) Interface: A Molecular Dynamics Simulation,” Japanese Journal of Applied Physics. 2010. link Times cited: 1 Abstract: The intermixing characteristics of Ti thin film deposited on… read moreAbstract: The intermixing characteristics of Ti thin film deposited on Al(001) substrate at atomic level were investigated by molecular dynamics simulation. The intermixing at Ti/Al(001) interface was limited within only the topmost layer of the Al(001) substrate at 300 K with 0.1 eV incident energy of a Ti atom. The mixing characteristics for Ti/Al(001) such as layer coverage function and mixing length were significantly different from those of the transition metals (TM; Fe, Co, and Ni)/Al(001) systems. The different intermixing behavior can be explained in terms of local acceleration and incorporation energy barrier. read less USED (high confidence) H. Gong, Y. He, and B.-yun Huang, “Bond strength and interface energy between Pd membranes and TiAl supports,” Applied Physics Letters. 2008. link Times cited: 26 Abstract: Intermetallic TiAl alloy is proposed as a promising support … read moreAbstract: Intermetallic TiAl alloy is proposed as a promising support for Pd membranes. First principles calculations reveal that coherent Pd/TiAl interfaces possess high values of bond strengths. Calculations also show that Ti-terminated (100) Pd/(100) TiAl and (110) Pd/(110) TiAl interfaces are energetically favorable with negative interface energies of about −3.1 J/m2, and that the bond strengths of Pd–Ti are bigger than those of Pd–Al. In addition, densities of states calculations suggest that a stronger chemical bonding is formed in the Pd/TiAl interface than corresponding Pd or TiAl bulks, which agrees well with similar experimental observations in literature. read less USED (high confidence) Y. Liu, L. Zhang, S. Q. Wang, and H. Ye, “Shear deformation in Ti3Al: atomic, dynamic and static simulations,” Modelling and Simulation in Materials Science and Engineering. 2007. link Times cited: 4 Abstract: The dynamical shear deformation-induced HCP → FCC process in… read moreAbstract: The dynamical shear deformation-induced HCP → FCC process in Ti3Al was systematically investigated using both molecular dynamics (MD) and ab initio methods. The details of the dislocation initiation, the microstructure evolution and the velocity field effect were presented and discussed. The MD simulation reveals that, with the increment of the velocity field, the deformation-induced dislocation slide may happen by three modes based on the nucleation of an initial FCC core, i.e. the continued fault slipping may initiate every other three layers, every other one and then three layers and every other one atomic layer. The corresponding transformed structure is an alternate existence of the single FCC and HCP plate, 18R fault, and the FCC plate containing three ABC units or more. The mechanism was further explored based on ab initio calculations of the detailed energy variation at different fault transition modes. The results promote systematic understanding of the stress induced fault transition mechanism in experimental observations. read less USED (high confidence) T. Boll, T. Al-Kassab, Y. Yuan, and Z.-guo Liu, “Computer Simulation of the Field Evaporation in Tial with Additions of Nb and Comparison with Experimental Results using a New Algorithmic Approach,” 2006 19th International Vacuum Nanoelectronics Conference. 2006. link Times cited: 0 Abstract: The formation of an image in a field ion microscope and the … read moreAbstract: The formation of an image in a field ion microscope and the field assisted evaporation of the surface atoms from atomic layers are simulated as an aid to tomographic atom probe analysis (TAP). Simulations are done for an gamma-TiAl-phase ordered structure with an L10 unit cell containing various additions of Nb while considering next neighbor binding energies between different partners. Algorithms that explore the vicinity around several species and analyze the degree of order based on TAP results are developed and tested on both experimental and simulated data read less USED (high confidence) A. Suzuki and Y. Mishin, “Interaction of Point Defects with Grain Boundaries in fcc Metals,” Interface Science. 2003. link Times cited: 76 USED (high confidence) R. Voskoboinikov, “Radiation Defects in Aluminum. Simulation of Primary Damage in Surface Collision Cascades,” Physics of Metals and Metallography. 2019. link Times cited: 6 USED (high confidence) D. Sun, “Proliferation of Twinning in Metals: Application to Magnesium Alloys.” 2018. link Times cited: 2 Abstract: In the search for new alloys with a great strength-to-weight… read moreAbstract: In the search for new alloys with a great strength-to-weight ratio, magnesium has emerged at the forefront. With a strength rivaling that of steel and aluminum alloys --- materials which are deployed widely in real world applications today --- but only a fraction of the density, magnesium holds great promise in a variety of next-generation applications. Unfortunately, the widespread adoption of magnesium is hindered by the fact that it fails in a brittle fashion, which is undesirable when it comes to plastic deformation mechanisms. Consequently, one must design magnesium alloys to navigate around this shortcoming and fail in a more ductile fashion. However, such designs are not possible without a thorough understanding of the underlying mechanisms of deformation in magnesium, which is somewhat contested at the moment. In addition to slip, which is one of the dominant mechanisms in metallic alloys, a mechanism known as twinning is also present, especially in hexagonal close-packed (HCP) materials such as magnesium. Twinning involves the reorientation of the material lattice about a planar discontinuity and has been shown as one of the preferred mechanisms by which magnesium accommodates out-of-plane deformation. Unfortunately, twinning is not particularly well-understood in magnesium, and needs to be addressed before progress can be made in materials design. In particular, though two specific modes of twinning have been acknowledged, various works in the literature have identified a host of additional modes, many of which have been cast aside as "anomalous" observations. To this end, we introduce a new framework for predicting the modes by which a material can twin, for any given material. Focusing on magnesium, we begin our investigation by introducing a kinematic framework that predicts novel twin configurations, cataloging these twins modes by their planar normal and twinning shear. We then subject the predicted twin modes to a series of atomistic simulations, primarily in molecular statics but with supplementary calculations using density functional theory, giving us insight on both the energy of the twin interface and barriers to formation. We then perform a stress analysis and identify the twin modes which are most likely to be activated, thus finding the ones most likely to affect the yield surface of magnesium. Over the course of our investigation, we show that many different modes actually participate on the yield surface of magnesium; the two classical modes which are accepted by the community are confirmed, but many additional modes --- some of which are close to modes which have been previously regarded as anomalies --- are also observed. We also perform some extensional work, showing the flexibility of our framework in predicting twins in other materials and in other environments and highlighting the complicated nature of twinning, especially in HCP materials. read less USED (high confidence) H. Sha, R. Faller, G. Tetiker, and P. Woytowitz, “Molecular Simulation Study of Aluminum – Noble Gas Interfacial Thermal Accommodation Coefficients,” Aiche Journal. 2018. link Times cited: 12 Abstract: Thermal accommodation coefficients (TAC) between aluminum an… read moreAbstract: Thermal accommodation coefficients (TAC) between aluminum and noble gases were studied with molecular dynamics (MD) simulations. Gases interacting with aluminum substrates were modeled by MD with gas velocities sampled from the Maxwell – Boltzmann distribution to give accumulated TAC results. Different implementations of the equation to calculate the TAC, which differ in the amount of information gleaned from MD and the corresponding simulation results, were carefully discussed. The best formula for molecular dynamics modeling in finite simulation time was determined. Additionally, the influence of the combining rules applied on aluminum – noble gas interatomic potential was characterized with the well-known Lennard – Jones 12 – 6 potential combined with Lorentz – Berthelot and Fender – Halsey mixing rules. The results were compared with experimental values and previous analytical model. TACs simulated with Fender – Halsey rules present excellent agreement with the experimental values. Detailed TAC distributions and accumulated TAC convergence are also included. This article is protected by copyright. All rights reserved. read less USED (high confidence) S. Ball, K. C. Alexander, and C. Schuh, “Stress-dependence of kinetic transitions at atomistic defects,” Modelling and Simulation in Materials Science and Engineering. 2017. link Times cited: 0 Abstract: The full second-rank activation volume tensors associated wi… read moreAbstract: The full second-rank activation volume tensors associated with vacancy migration in FCC copper and HCP titanium as well as transition events in the Σ5 (2 1 0) grain boundary in copper are calculated and analyzed. The full tensorial results quantitatively illustrate how the conventional use of an activation volume scalar in atomistic studies of the kinetic processes of complex defects can miss important stress dependencies, in that neither hydrostatic pressure nor deviatoric stress dependencies can be considered alone as dominating the response. The results speak to the importance of anisotropies in the stress-dependence of atomistic kinetics, including crystal structure anisotropy, elastic anisotropy, and defect structure or migration-path anisotropies. read less USED (high confidence) J. Raush, “Thermophysical and Thermochemical Property Measurement and Prediction of Liquid Metal Titanium Alloys with Applications in Additive Manufacturing.” 2016. link Times cited: 0 Abstract: ............................................................… read moreAbstract: ........................................................................................................................................ xv Chapter 1 Motivation ...................................................................................................................... 1 1.1 Engineering Challenges.................................................................................................... 1 1.1.1 Additive Manufacturing ........................................................................................... 2 1.1.2 Powder Metallurgy.................................................................................................... 3 1.2 Materials Development Approach ................................................................................... 4 1.3 Focus of this Research...................................................................................................... 8 1.3.1 Objectives ............................................................................................................... 11 1.3.2 Project Timeline and Funding ................................................................................. 12 1.4 Outline of Dissertation ................................................................................................... 12 Chapter 2 Testing and Modeling Background .............................................................................. 14 2.1 Testing and Characterization of Liquid Metals .............................................................. 14 2.1.1 Traditional Thermophysical Property Measurement Techniques ........................... 14 2.1.2 Electrostatic Levitation ........................................................................................... 16 2.1.3 Additional Containerless Testing Techniques ........................................................ 31 2.2 Numerical Modeling ...................................................................................................... 31 2.2.1 CALPHAD .............................................................................................................. 32 2.2.2 Molecular Dynamics ............................................................................................... 33 Chapter 3 Test Method.................................................................................................................. 36 3. read less USED (high confidence) H. Zong, X. Ding, T. Lookman, J. Li, and J. Sun, “Uniaxial stress-driven coupled grain boundary motion in hexagonal close-packed metals: A molecular dynamics study,” Acta Materialia. 2015. link Times cited: 29 USED (low confidence) S. Hayakawa and H. Xu, “Development of an interatomic potential for L12 precipitates in Fe–Ni–Al alloys,” Computational Materials Science. 2024. link Times cited: 0 USED (low confidence) Y. Ding et al., “Effect of shell thickness on mechanical behavior of Al/Ti core-shell nanowires during three-point bending and unloading,” Mechanics of Materials. 2023. link Times cited: 0 USED (low confidence) X. Lu, H. Ran, Q. Cheng, F. Guo, and C. Huang, “Underlying mechanisms of enhanced plasticity in Ti/Al laminates at elevated temperatures: A molecular dynamics study,” Journal of Materials Research and Technology. 2023. link Times cited: 0 USED (low confidence) A. Khoei, M. R. Seddighian, and A. R. Sameti, “Machine learning-based multiscale framework for mechanical behavior of nano-crystalline structures,” International Journal of Mechanical Sciences. 2023. link Times cited: 0 USED (low confidence) P. Wang et al., “Molecular dynamic simulations of the martensitic transformation for the dual-phase structure and dislocation activities in Ti80 alloys,” Mechanics of Materials. 2023. link Times cited: 0 USED (low confidence) T. Yang, X. Han, W. Li, X. Chen, and P. Liu, “Angular dependent potential for Al-Zr binary system to study the initial heterogeneous nucleation behavior of liquid Al on L12-Al3Zr,” Computational Materials Science. 2023. link Times cited: 0 USED (low confidence) X. G. Song, Y. Luo, S. P. Hu, Y. X. Wang, Y. Z. Liu, and J. Cao, “Enhancing interfacial strength of T-joint for vacuum-brazed thin-walled structures comprising TiAl and GH3536 alloys via in-situ synthesis of Al2TiO5 ceramic coatings,” Journal of Materials Research and Technology. 2023. link Times cited: 0 USED (low confidence) D. Zhang et al., “How confined spaces induce layered crystallization of Al-Ti alloys,” Materials Today Communications. 2023. link Times cited: 0 USED (low confidence) I. Aditya, “Electronic and Surface Properties of Aluminum (111) Surface Modified by Interstitial and Substitutional Titanium Incorporation,” Indonesian Journal of Physics. 2023. link Times cited: 0 Abstract: This study investigates the influence of interstitial and su… read moreAbstract: This study investigates the influence of interstitial and substitutional titanium atoms on the electronic properties of aluminum surfaces using density functional theory (DFT). The study focuses on three variables: the presence and arrangement of Ti interstitials on the aluminum surface, the behavior of Ti substitutional and interstitial impurities, and the energetic stability and structural properties of these systems. Multiple DFT methods are employed to derive conclusions regarding the impact of these variables on the surface properties of aluminum. The study provides valuable insights into how different states of interstitial and substitutional Ti can alter the physical characteristics and performance behaviors of the aluminum surface. The understanding of these effects could enable engineers to design more efficient materials with enhanced properties suitable for various industries. read less USED (low confidence) M. Alam and A. N. Gandi, “Mechanical and thermodynamic properties of γ-TiAl using first-principles calculations,” Modelling and Simulation in Materials Science and Engineering. 2023. link Times cited: 0 Abstract: Temperature dependence of structural, mechanical, and thermo… read moreAbstract: Temperature dependence of structural, mechanical, and thermodynamic properties of γ-TiAl is modeled using an extended quasi-harmonic approximation and first-principles calculations. In the first step, the volumes are estimated as a function of temperature following the quasi-harmonic approximation. The lattice parameters are further optimized at fixed volumes in the second step. Modeled mechanical properties (bulk modulus, shear modulus, Young’s modulus, Poisson’s ratio, and hardness) agree with the experimentally reported mechanical properties. Similarly, the modeled thermodynamic properties (entropy, heat capacity at constant pressure, Gibbs free energy) are in good agreement with the thermodynamic properties reported from experiments and CALculation of PHAse Diagrams approaches. This study suggests that further optimization of the degree of freedom in the unit cell improves the model accuracy of properties estimated following the quasi-harmonic approximation. read less USED (low confidence) H. Cao et al., “Numerical simulation of nano-cutting behaviors for polycrystalline γ-TiAl alloy: The effect of grain sizes,” Journal of Manufacturing Processes. 2023. link Times cited: 0 USED (low confidence) H. Cao et al., “Molecular dynamics simulation of the effect of supersonic fine particle bombardment on the mechanical behaviour of γ-TiAl alloy: The effect of grain size,” Vacuum. 2023. link Times cited: 0 USED (low confidence) R. E. Voskoboinikov, “MD Simulations of Collision Cascades in α-Ti. The Residual Number of Radiation Defects, Cascade Relaxation Time, and Displacement Cascade Region Morphology,” Physics of Metals and Metallography. 2023. link Times cited: 1 USED (low confidence) Z. Guo et al., “Atomic simulation for the effect of nano-cutting parameters on the 3D surface morphology of polycrystalline γ-TiAl alloy,” Modelling and Simulation in Materials Science and Engineering. 2023. link Times cited: 0 Abstract: γ-TiAl alloy is one of the most potentially lightweight and … read moreAbstract: γ-TiAl alloy is one of the most potentially lightweight and high-temperature structural materials, and its machined surface quality has a significant effect on member service performance. Despite the extensive research on plastic removal and defect evolution under different cutting parameters, the forming mechanism of surface topography is not perfect under different cutting parameters. It is necessary to study the variation law of surface topography under the influence of different cutting parameters from the atomic scale. To this end, the influence of cutting depths and cutting speeds on the machined surface topography is investigated during nano-cutting of polycrystalline γ-TiAl alloys based on molecular dynamics simulation methods, and the effect of defective grain boundaries on cutting force fluctuations is analyzed. The results show that the effect of grain boundary on material deformation and dislocation obstruction is the main reason for the peak cutting force; with the increase of cutting depth, the average cutting force and friction coefficient increase, and both Sa and Sq show an increasing trend, which is the result of the joint action of plowing effect and grain boundary distribution; Sa and Sq show a decreasing and then increasing trend with the increase of cutting speed, and the critical cutting speed is 200 m s−1. This indicates that a smaller cutting depth and an appropriately higher cutting speed can effectively improve the surface quality of the polycrystalline γ-TiAl alloy, and optimize its nano-cutting process. read less USED (low confidence) Z. Ma and Z. Pan, “Efficient machine learning of solute segregation energy based on physics-informed features,” Scientific Reports. 2023. link Times cited: 0 USED (low confidence) T.-M. Lin, S.-xia Liu, P. Qu, and X. Zhao, “Investigation on plastic deformation mechanism of gradient nano-polycrystalline pure titanium by atomic simulation,” Vacuum. 2023. link Times cited: 0 USED (low confidence) H. Guo et al., “Planar slip triggered by successive dislocation-precipitate interaction in titanium alloys,” Materials Science and Engineering: A. 2023. link Times cited: 0 USED (low confidence) T. Li, C. Tian, A. Moridi, and J. Yeo, “Elucidating Interfacial Dynamics of Ti-Al Systems Using Molecular Dynamics Simulation and Markov State Modeling,” ACS applied materials & interfaces. 2023. link Times cited: 0 Abstract: Due to their remarkable mechanical and chemical properties, … read moreAbstract: Due to their remarkable mechanical and chemical properties, Ti-Al-based materials are attracting considerable interest in numerous fields of engineering, such as automotive, aerospace, and defense. With their low density, high strength, and resistance to corrosion and oxidation, these intermetallic alloys and metal-compound composites have found diverse applications. However, additive manufacturing and heat treatment of Ti-Al alloys frequently lead to brittleness and severe formation of defects. The present study delves into the interfacial dynamics of these Ti-Al systems, particularly focusing on the behavior of Ti and Al atoms in the presence of TiAl3 grain boundaries under experimental heat treatment conditions. Using a combination of molecular dynamics and Markov state modeling, we scrutinize the kinetic processes involved in the formation of TiAl3. The molecular dynamics simulation indicates that at the early stage of heat treatment, the predominating process is the diffusion of Al atoms toward the Ti surface through the TiAl3 grain boundaries. Markov state modeling identifies three distinct dynamic states of Al atoms within the Ti/Al mixture that forms during the process, each exhibiting a unique spatial distribution. Using transition time scales as a qualitative measure of the rapidness of the dynamics, it is observed that the Al dynamics is significantly less rapid near the Ti surface compared to the Al surface. Put together, the results offer a comprehensive understanding of the interfacial dynamics and reveal a three-stage diffusion mechanism. The process initiates with the premelting of Al, proceeds with the prevalent diffusion of Al atoms toward the Ti surface, and eventually ceases as the Ti concentration within the mixture progressively increases. The insights gained from this study could contribute significantly to the control and optimization of manufacturing processes for these high-performing Ti-Al-based materials. read less USED (low confidence) Z. Yu et al., “Atomic simulation of the effect of supersonic fine particle bombardment process parameters on the mechanical properties of polycrystalline γ-TiAl alloy,” Modelling and Simulation in Materials Science and Engineering. 2023. link Times cited: 1 Abstract: γ-TiAl alloys are the most promising lightweight high-temper… read moreAbstract: γ-TiAl alloys are the most promising lightweight high-temperature structural materials, but the materials often fail from the surface, which is mainly attributed to the stress state of the material surface. In this paper, the orthogonal experiment method and molecular dynamics modeling are used to choose a set of the best process parameters for supersonic fine particle bombardment (SFPB). Furthermore, by determining the optimal process parameters, this study examines the influence of residual stress distribution on the mechanical properties of the material under various process conditions. The simulation results reveal that the residual stress distribution is minimally impacted by particle radius, nonetheless, maintaining a moderate level of compressive residual stress within a specific range can substantially augment both the tensile strength and indentation hardness. An increase in the number of particles results in a more uniform distribution of surface residual stresses. Conversely, an increase in the number of impacts causes stress concentration to intensify at the particle’s contact point, and thus a deeper distribution of residual stress is observed. This study illustrates how the mechanical properties of polycrystalline γ-TiAl alloy are affected by the process parameters of SFPB in terms of atomic size in order to develop and select the optimal SFPB parameters. read less USED (low confidence) J. Lu, J. Wang, K. Wan, Y. Chen, H. Wang, and X. Shi, “An accurate interatomic potential for the TiAlNb ternary alloy developed by deep neural network learning method.,” The Journal of chemical physics. 2023. link Times cited: 0 Abstract: The complex phase diagram and bonding nature of the TiAl sys… read moreAbstract: The complex phase diagram and bonding nature of the TiAl system make it difficult to accurately describe its various properties and phases by traditional atomistic force fields. Here, we develop a machine learning interatomic potential with a deep neural network method for the TiAlNb ternary alloy based on a dataset built by first-principles calculations. The training set includes bulk elementary metals and intermetallic structures with slab and amorphous configurations. This potential is validated by comparing bulk properties-including lattice constant and elastic constants, surface energies, vacancy formation energies, and stacking fault energies-with their respective density functional theory values. Moreover, our potential could accurately predict the average formation energy and stacking fault energy of γ-TiAl doped with Nb. The tensile properties of γ-TiAl are simulated by our potential and verified by experiments. These results support the applicability of our potential under more practical conditions. read less USED (low confidence) Z. Zhen et al., “Transformation of non-screw super-dislocation dipoles in M3Al (M=Ni, Fe, Ti) intermetallics: high-throughput atomistic modeling,” Journal of Alloys and Compounds. 2023. link Times cited: 0 USED (low confidence) Z. Yu et al., “Phase transformation behavior of aluminum under high hydrostatic pressure: A molecular dynamics study,” Materials Today Communications. 2023. link Times cited: 0 USED (low confidence) Q.-liang Kang, X. Xu, G. Wang, T. Zhou, and C.-xiong Wang, “Enhanced high temperature oxidation resistance of discontinuous distributed TiBw reinforced TA15 titanium alloy by simple pack cementation method,” Corrosion Science. 2023. link Times cited: 2 USED (low confidence) K. A. Nair and S. Ghosh, “Crack tip enhanced phase-field model for crack evolution in crystalline Ti6Al from concurrent crystal plasticity FE-molecular dynamics simulations,” European Journal of Mechanics - A/Solids. 2023. link Times cited: 1 USED (low confidence) Y. Gao et al., “Investigation of the atomic-level microstructural evolution of quadruple-fused α/β titanium particles during sintering,” Journal of Molecular Liquids. 2023. link Times cited: 0 USED (low confidence) T. Schmalofski, M. Kroll, H. Dette, and R. Janisch, “Towards active learning: A stopping criterion for the sequential sampling of grain boundary degrees of freedom,” Materialia. 2023. link Times cited: 0 USED (low confidence) Y. Xu, H. Fan, Z. Li, and Y. Zhou, “Signatures of anharmonic phonon transport in ultrahigh thermal conductance across atomically sharp metal/semiconductor interface,” International Journal of Heat and Mass Transfer. 2023. link Times cited: 4 USED (low confidence) B. Zhai and H. P. Wang, “Accurate interatomic potential for the nucleation in liquid Ti-Al binary alloy developed by deep neural network learning method,” Computational Materials Science. 2023. link Times cited: 2 USED (low confidence) Y. Gao et al., “Design of Functionally Graded Ti–Al Alloy with Adjustable Mechanical Properties: a Molecular Dynamics Insights,” Journal of Materials Research and Technology. 2023. link Times cited: 4 USED (low confidence) B. Waters, D. S. Karls, I. Nikiforov, R. Elliott, E. Tadmor, and B. Runnels, “Automated determination of grain boundary energy and potential-dependence using the OpenKIM framework,” Computational Materials Science. 2022. link Times cited: 5 USED (low confidence) B. Wei et al., “Influence of Lowering Basal Stacking Fault Energy on Twinning Behaviours,” Acta Materialia. 2022. link Times cited: 7 USED (low confidence) Y. Chen et al., “Unraveling hot deformation behavior and microstructure evolution of nanolamellar TiAl/Ti3Al composites,” Intermetallics. 2022. link Times cited: 0 USED (low confidence) H. Song et al., “Hall–Petch relationship in Ti3Al nano-polycrystalline alloys by molecular dynamics simulation,” Journal of Materials Science. 2022. link Times cited: 1 USED (low confidence) S. K. Maurya, S. Chandra, J. Nie, and A. Alankar, “Crack mediated dislocation activities in Al/Ti nanolayered composites: an atomistic study,” Modelling and Simulation in Materials Science and Engineering. 2022. link Times cited: 0 Abstract: In this work, to understand crack propagation in Al/Ti nanol… read moreAbstract: In this work, to understand crack propagation in Al/Ti nanolayered composites, a series of molecular dynamic simulations were performed with crack in different layers of the nanolayered composites and subjected to mode I loading. Nanolayered composite with a crack in Al layer, and monolithic Al show ductile fracture behavior that occurs by nucleation of Shockley partial dislocation at the crack tip. On the other hand, the fracture behavior in nanolayered composites with a crack in Ti shows crack bowing which is similar to the brittle fracture, and subsequent crack trapping at the interface. However, monolithic Ti shows typical cleavage fracture followed by activation of basal and pyramidal ⟨c+a⟩ slip that blunts the crack leading to ductile fracture. When the crack is in the Ti layer, the other Ti layers in a nanolayered composite deform by prismatic and pyramidal ⟨c+a⟩ slip. However, the Ti layer deforms only via slip on prismatic planes when the crack is in the Al layer. Critical strain energy release rate G c based continuum analysis predicts the fracture mode in monolithic Ti correctly, but it fails to predict the fracture mode in monolithic Al and nanolayered composites with crack in the Al layer. It is found that the G c determined based on external loading is marginally higher when the crack is in the Al layer as compared against the case when the crack is in the Ti layer. The G c value for the basal and pyramidal slip in Ti is higher than the G c value for cleavage. This poses an interesting phenomenon since the G c in monolithic Al is found to be much lower than that of monolithic Ti. The reason is attributed to the constrained plasticity in the presence of an Al/Ti interface. read less USED (low confidence) T. Gao et al., “Molecular dynamics simulations on the connectivity of topologically close-packed clusters in TiAl3 alloys,” Physica Scripta. 2022. link Times cited: 0 Abstract: Presently, there has been increasing attention on TiAl3, whi… read moreAbstract: Presently, there has been increasing attention on TiAl3, which is commonly used for fabricating power aviation devices owing to its good oxidation resistance and outstanding mechanical properties in high-temperature. As the microstructures determine the macroscopic properties of a material, we investigated the connectivity of icosahedral central atoms in TiAl3 using conventional methods in this study. The topologically close-packed (TCP) structures are present in supercooled liquids, metallic glasses, and metallic liquids. They are intrinsic to liquid metals and are an essential character of the structure in metallic glasses (MGs). However, because of the lack of the concept of connectivity of the TCP structures, we investigated connectivity from the icosahedral central atoms to TCP structures, and a formula was proposed to calculate the connectivity of the TCP structures. Based on the results, low temperatures and cooling rates are conducive to generate high connectivity between icosahedral central atoms and TCP structures. The proposed formula can characterize the connectivity of the TCP structures. These findings open new opportunities for conducting research on the connectivity of clusters in binary alloys. read less USED (low confidence) C. Liang, W. B. Liu, and H. P. Wang, “Enhanced tensile properties and intersecting nanotwins formation mechanism of Ti44Al48Nb8 alloy via electromagnetic levitation processing,” International Journal of Plasticity. 2022. link Times cited: 5 USED (low confidence) H. Men and Z. Fan, “Molecular Dynamics Simulations on Effect of Surface Roughness of Amorphous Substrate on Nucleation in Liquid Al,” Metals. 2022. link Times cited: 2 Abstract: In this study, we used molecular dynamics (MD) simulations t… read moreAbstract: In this study, we used molecular dynamics (MD) simulations to investigate the atomic ordering in the liquid aluminum (Al) adjacent to the amorphous substrate with smooth and rough surfaces. This study revealed that the liquid exhibited layering within about 5 atomic layers but no visible in-plane atomic ordering at the interface with the smooth amorphous surface, and neither layering nor in-plane atomic ordering with the rough surface of the amorphous substrate. However, the smooth amorphous surface induced some local ordered structure in the liquid at the interface by a structural templating mechanism, which promoted heterogeneous nucleation by creating a 2-dimensional (2D) nucleus in the third layer. The amorphous substrate with a rough surface had no effect on the nucleation in the liquid, leading to the occurrence of homogeneous nucleation with an undercooling 100 K larger than that of heterogeneous nucleation on the smooth amorphous substrate. This study confirmed that structural templating is a general mechanism for heterogeneous nucleation. read less USED (low confidence) L. C. Liu, S. F. Zhou, and H. Gong, “Cohesion properties and hydrogen permeation at PdCu/TiAl interface,” Surface Science. 2022. link Times cited: 1 USED (low confidence) Z. Li et al., “Liquid-Liquid Phase Transition in Metallic Droplets.,” The journal of physical chemistry. A. 2022. link Times cited: 1 Abstract: We report theoretical evidence of the substrate-induced liqu… read moreAbstract: We report theoretical evidence of the substrate-induced liquid-liquid phase transition (LLPT) behaviors in a single Al droplet and Ti-Al droplets. The Al droplet can produce an LLPT induced by substrates in part, forming a special three-layer structure. However, the introduction of a Ti droplet can promote the LLPT in an Al droplet. Al and Ti droplets do not coalesce into a homogeneously mixed droplet but produce the ordered liquid films. The substrate-induced LLPT in the Al droplet is characterized by the transition from the disordered to ordered structure. Results indicate that the substrate and the Ti droplet are the driving forces to promote the LLPT. The LLPT of the Ti-Al droplets in the wedge-shaped substrate is also observed, indicating that the confined Ti-Al droplets are more likely to undergo an LLPT. read less USED (low confidence) H. Zhang, B. Wei, X. Ou, S. Ni, K. Zhou, and M. Song, “Dislocation induced FCC twinning at the HCP/FCC interfaces in a deformed Ti-5at.%Al alloy: Experiments and simulations,” Journal of Physics and Chemistry of Solids. 2022. link Times cited: 1 USED (low confidence) H. Liu, X. Guo, X. Pang, J. Zhao, and Q. Zhang, “Effects of current rate on electrically exploding aluminum wires in argon gas,” AIP Advances. 2022. link Times cited: 0 Abstract: The electrically exploding wires (EEWs) method is a low-cost… read moreAbstract: The electrically exploding wires (EEWs) method is a low-cost, high-efficiency method for nanoparticle preparation. The current parameter is a determining factor of EEWs’ characteristics and nanoparticles’ size distribution. This paper systematically investigates the effects of the current rate on the resistive stage and diffusion process of EEWs in argon gas. The electrical measurement indicated that EEWs tend to transform from current-pause mode to direct-breakdown mode as the current rate increases. Deposited energy increases with the current rate approximately linearly due to improved power and overheating limits. Spatial inhomogeneities include residual cores, irregular discharge channels, local hot spots, and stratification structures. The residual core is formed because of the rivalry between the vaporized part and the condensed wire core. Increasing the current rate suppresses the above-mentioned inhomogeneities and accelerates diffusion. read less USED (low confidence) M. G. Urazaliev, M. E. Stupak, and V. Popov, “An Atomistic Simulation of Special Tilt Boundaries in α-Ti: Structure, Energy, Point Defects, and Grain-Boundary Self-Diffusion,” Physics of Metals and Metallography. 2022. link Times cited: 0 USED (low confidence) J. Li, X. Dong, H. Xie, C. Xu, J. Liu, and J. Zhang, “Process-induced evolution of prismatic dislocation loop and its effect on mechanical properties,” Materials Today Communications. 2022. link Times cited: 1 USED (low confidence) D. Wen, B. Kong, S. Wang, L. Liu, Q. Song, and Z. Yin, “Mechanism of stress- and thermal-induced fct → hcp → fcc crystal structure change in a TiAl-based alloy compressed at elevated temperature,” Materials Science and Engineering: A. 2022. link Times cited: 2 USED (low confidence) J. Lyu, R. Elman, L. Svyatkin, and V. Kudiiarov, “Theoretical and Experimental Research of Hydrogen Solid Solution in Mg and Mg-Al System,” Materials. 2022. link Times cited: 9 Abstract: The study of hydrogen storage properties of Mg-based thin fi… read moreAbstract: The study of hydrogen storage properties of Mg-based thin films is of interest due to their unique composition, interface, crystallinity, and high potential for use in hydrogen-storage systems. Alloying Mg with Al leads to the destabilization of the magnesium hydride reducing the heat of reaction, increases the nucleation rate, and decreases the dehydriding temperature. The purpose of our study is to reveal the role of the aluminum atom addition in hydrogen adsorption and accumulation in the Mg-H solid solution. Ab initio calculations of aluminum and hydrogen binding energies in magnesium were carried out in the framework of density functional theory. Hydrogen distribution and accumulation in Mg and Mg-10%Al thin films were experimentally studied by the method of glow-discharge optical emission spectroscopy and using a hydrogen analyzer, respectively. It was found that a hydrogen distribution gradient is observed in the Mg-10%Al coating, with more hydrogen on the surface and less in the bulk. Moreover, the hydrogen concentration in the Mg-10%Al is lower compared to Mg. This can be explained by the lower hydrogen binding energy in the magnesium-aluminum system compared with pure magnesium. read less USED (low confidence) L. Chang, X. Liu, J. Zhao, and C.-yu Zhou, “Effect of interatomic potential on modelling fracture behavior in hcp titanium: A molecular dynamics study,” Journal of Materials Research and Technology. 2022. link Times cited: 3 USED (low confidence) H. Zhang, B. Wei, X. Ou, S. Ni, H. Yan, and M. Song, “Atomic-level study of 101¯1 deformation twinning in pure Ti and Ti-5at.% Al alloy,” International Journal of Plasticity. 2022. link Times cited: 8 USED (low confidence) W. Li et al., “Mechanical stability of lamellar microstructure in TiAl:An atomic-scale study,” Journal of Materials Research and Technology. 2022. link Times cited: 0 USED (low confidence) R. Voskoboinikov, “A Study of Primary Damage Formation in Collision Cascades in Titanium,” Inorganic Materials: Applied Research. 2022. link Times cited: 1 USED (low confidence) L. Chang, Z. Tao, S. Yang, X. Liu, and C.-yu Zhou, “Anisotropic deformation behavior of 112-0, 101-0 and 0001-textured nanocrystalline titanium,” Results in Physics. 2022. link Times cited: 0 USED (low confidence) J. Wang, Q.-Y. Li, Z. Lu, H. Wang, X.-G. Lu, and Y. Chen, “The effect of impurities on stacking fault energy and dislocation properties in γ-TiAl,” Vacuum. 2022. link Times cited: 8 USED (low confidence) A. Neogi and R. Janisch, “Unravelling the lamellar size-dependent fracture behavior of fully lamellar intermetallic γ-TiAl,” Acta Materialia. 2022. link Times cited: 12 USED (low confidence) H. Xiang and W. Guo, “A newly developed interatomic potential of Nb−Al−Ti ternary systems for high-temperature applications,” Acta Mechanica Sinica. 2022. link Times cited: 0 USED (low confidence) Y. Gao et al., “Evolution of dislocation and twin structures in Ti3Al during solidification,” Vacuum. 2021. link Times cited: 11 USED (low confidence) H. Zhang, X. Ou, X. Zhang, H. Yan, K. Zhou, and M. Song, “Effects of Al on crack propagation in titanium alloys and the governing toughening mechanism,” Mechanics of Materials. 2021. link Times cited: 4 USED (low confidence) H. Xiang and W. Guo, “nSynergistic effects of twin boundary and phase boundary for enhancing ultimate strength and ductility of lamellar TiAl single crystals,” International Journal of Plasticity. 2021. link Times cited: 20 USED (low confidence) H. Ganesan, I. Scheider, and C. Cyron, “Understanding creep in TiAl alloys on the nanosecond scale by molecular dynamics simulations,” Materials & Design. 2021. link Times cited: 3 USED (low confidence) J.-yao Liu and L. Zhang, “Molecular Dynamics Simulation of the Tensile Deformation Behavior of the γ(TiAl)/α2(Ti3Al) Interface at Different Temperatures,” Journal of Materials Engineering and Performance. 2021. link Times cited: 3 USED (low confidence) Z. Liu et al., “Different Connection Models of Icosahedral Structures in TiAl Alloy Caused by the Cooling Rates,” physica status solidi (b). 2021. link Times cited: 0 Abstract: High‐quality TiAl alloy is used to fabricate aerospace equip… read moreAbstract: High‐quality TiAl alloy is used to fabricate aerospace equipment with excellent mechanical properties because of its interesting properties, including low density, high specific yield strength, and better corrosion resistance. However, the fabrication of high‐quality TiAl alloy is challenging because the connection mechanism between different types of clusters in TiAl alloy during the rapid cooling process is not clear. This study uses molecular dynamics (MD) simulation methods to study the connection models of icosahedral (ICO) structures and other defective ICO structures at different cooling rates. The ICO structures represent the short‐range ordered structure in the system. Moreover, the complex connections between the ICO and its defective structures constitute the basic structural features of TiAl metallic glass. The results show that the connections between ICO and its defective structures differ significantly with the cooling rate. It is easier to form a more complex nanostructure connected by the ICO structures with higher proportion of Al central atoms at the lower cooling rate. As the temperature drops at the same rate, the number of Al central atoms with smaller atomic radius in the icosahedrons increases gradually, giving them an absolute advantage. read less USED (low confidence) A. Kedharnath, R. Kapoor, and A. Sarkar, “Classical molecular dynamics simulations of the deformation of metals under uniaxial monotonic loading: A review,” Computers & Structures. 2021. link Times cited: 16 USED (low confidence) J. Li, M. Sui, and B. Li, “A half-shear-half-shuffle mechanism and the single-layer twinning dislocation for 112¯2〈112¯3¯〉 mode in hexagonal close-packed titanium,” Acta Materialia. 2021. link Times cited: 10 USED (low confidence) Y. Liu et al., “New phase transition pattern of fivefold twins transformed into lamellar structure in Ti3Al alloy,” CrystEngComm. 2021. link Times cited: 1 Abstract: The structures of fivefold twin (FFT) and lamellar (LAM) are… read moreAbstract: The structures of fivefold twin (FFT) and lamellar (LAM) are the primary configurations during the crystallization of alloys. However, the co-existence of two structures in one system and conversion mechanism... read less USED (low confidence) X. Chen et al., “Machine learning enhanced empirical potentials for metals and alloys,” Comput. Phys. Commun. 2021. link Times cited: 5 USED (low confidence) Y. Émurlaeva et al., “On the texture and superstructure formation in Ti–TiAl3–Al MIL composites,” Intermetallics. 2021. link Times cited: 7 USED (low confidence) S. Kiselev and V. Kiselev, “Numerical Simulation of Fracture of Titanium and Aluminum Nanocrystals by the Molecular Dynamics Method,” Combustion, Explosion, and Shock Waves. 2021. link Times cited: 0 USED (low confidence) Dong-Lin 栋林 Luan 栾, Y. Wang 王, G. Li 李, Lei 磊 Yuan 袁, and J. Chen 陈, “Plasticity and melting characteristics of metal Al with Ti-cluster under shock loading,” Chinese Physics B. 2021. link Times cited: 0 Abstract: Impurity agglomeration has a significant influence on shock … read moreAbstract: Impurity agglomeration has a significant influence on shock response of metal materials. In this paper, the mechanism of Ti-clusters in metal Al under shock loading is investigated by non-equilibrium molecular dynamics simulations. Our results show that the Ti-cluster has obvious effects on the dislocation initiation and melting of bulk Al. First, the Ti clusters induces the strain concentrate and leads the dislocations to be initiated from the interface of Ti cluster. Second, dislocation distribution from the Ti-cluster model results in a formation of a grid-like structure, while the dislocation density is reduced compared with that from the perfect Al model. Third, the critical shock velocity of dislocation from the Ti-cluster model is lower than from perfect Al model. Furthermore, it is also found that the temperature near the interface of Ti-cluster is 100 K-150 K higher than in the other areas, which means that Ti-cluster interface melts earlier than the bulk area. read less USED (low confidence) S. Kiselev and V. Kiselev, “Numerical Simulation of Fracture of Titanium and Aluminum Nanocrystals by the Molecular Dynamics Method,” Combustion, Explosion, and Shock Waves. 2021. link Times cited: 1 Abstract: Results of numerical simulations of fracture of titanium and… read moreAbstract: Results of numerical simulations of fracture of titanium and aluminum nanocrystals by the molecular dynamics method are reported. The nanocrystals are subjected to uniaxial tension in a wide temperature range (300–1270 K). It is demonstrated that tension of titanium nanocrystals heated to temperatures above 0.7 of the melting temperature in a non-stressed nanocrystal first leads to a phase transition from the crystalline to liquid state, followed by fracture. This effect is not observed in the case of tension of the aluminum nanocrystal. read less USED (low confidence) R. Fu, Z. Rui, Y. Dong, D. Luo, and C. Yan, “Effects of γ/γ lamellar interfaces on interlamellar crack propagation behaviors of TiAl alloys,” Computational Materials Science. 2021. link Times cited: 5 USED (low confidence) A. A. Schratt, I. Steinbach, and V. Mohles, “Grain boundary energy landscape from the shape analysis of synthetically stabilized embedded grains,” Computational Materials Science. 2021. link Times cited: 2 USED (low confidence) A. Chauniyal, G. Dehm, and R. Janisch, “On the role of pre-existing defects in influencing hardness in nanoscale indentations — Insights from atomistic simulations,” Journal of The Mechanics and Physics of Solids. 2021. link Times cited: 7 USED (low confidence) R. Rozas, L. G. Macdowell, P. Toledo, and J. Horbach, “Crystal growth of bcc titanium from the melt and interfacial properties: A molecular dynamics simulation study.,” The Journal of chemical physics. 2021. link Times cited: 5 Abstract: The crystal growth kinetics and interfacial properties of ti… read moreAbstract: The crystal growth kinetics and interfacial properties of titanium (Ti) are studied using molecular dynamics computer simulation. The interactions between the Ti atoms are modeled via an embedded atom method potential. First, the free solidification method (FSM) is used to determine the melting temperature Tm at zero pressure where the transition from liquid to body-centered cubic crystal occurs. From the simulations with the FSM, the kinetic growth coefficients are also determined for different orientations of the crystal, analyzing how the coupling to the thermostat affects the estimates of the growth coefficients. At Tm, anisotropic interfacial stiffnesses and free energies as well as kinetic growth coefficients are determined from capillary wave fluctuations. The so-obtained growth coefficients from equilibrium fluctuations and without the coupling of the system to a thermostat agree well with those extracted from the FSM calculations. read less USED (low confidence) S. K. Maurya, J. Nie, and A. Alankar, “Atomistic analyses of HCP-FCC transformation and reorientation of Ti in Al-Ti multilayers,” Computational Materials Science. 2021. link Times cited: 8 USED (low confidence) S. Kiselev, “NUMERICAL SIMULATION OF FRACTURE OF NANOCRYSTALS OF THE TiAl3 INTERMETALLIC COMPOUND BY THE MOLECULAR DYNAMICS METHOD,” Journal of Applied Mechanics and Technical Physics. 2021. link Times cited: 0 USED (low confidence) Z. Zhen et al., “Dislocation self-interaction in TiAl: Evolution of super-dislocation dipoles revealed by atomistic simulations,” Journal of Materials Science & Technology. 2021. link Times cited: 7 USED (low confidence) B. Bertin, J. Durinck, J. Grilhé, and J. Colin, “Grain boundary-induced plasticity during thin film buckling,” Mechanics of Materials. 2021. link Times cited: 3 USED (low confidence) Y. Zeng and X. Li, “Atomistic simulations of high-temperature creep in nanotwinned TiAl alloys,” Extreme Mechanics Letters. 2021. link Times cited: 6 USED (low confidence) A. Neogi and R. Janisch, “Twin-Boundary Assisted Crack Tip Plasticity and Toughening in Lamellar γ-TiAl,” Mechanical Properties & Deformation of Materials eJournal. 2021. link Times cited: 23 Abstract: The internal twin-boundaries in lamellar γ-TiAl alloys, name… read moreAbstract: The internal twin-boundaries in lamellar γ-TiAl alloys, namely true-twin (TT), rotational boundary(RB), and pseudo-twin (PT), are known to be effective in strengthening the TiAl microstructures. Nevertheless, for designing microstructures with optimised mechanical properties, a better understanding of the role of these boundaries on fracture behavior is still required. To this end, we study how and to what degree crack advancement is affected by the local lattice orientation and atomic structure at the various twin boundaries. Molecular statics simulations were performed in conjunction with a linear elastic fracture mechanics based analysis, to understand the inter-lamellar and as well as trans-lamellar crack advancement at a TT, RB, and PT interface. The fracture toughness as well as the crack advancement mechanisms of the inter-lamellar cracks depend critically on the propagation direction. For instance, cracks along ⟨11‾2] in the TT, RB, and PT plane always emit dislocations at the crack tip, while the cracks along the opposite direction are brittle in nature. When it comes to trans-lamellar crack advancement, the crack tip shows significant plastic deformation and toughening for all inter-faces. However, at a TT, a brittle crack is able to penetrate through the interface at a higher applied load, and propagates in the adjacent γ′ phase, while in the case of RB and PT, the crack tip is blunted and arrested at or near the boundary, resulting in dislocation emission and crack tip toughening. This suggests that a variation of the sequence of the different rotational boundaries could be a possibility to tune the crack tip plasticity and toughening in lamellar TiAl. read less USED (low confidence) A. Rajput and S. Paul, “Effect of soft and hard inclusions in tensile deformation and damage mechanism of Aluminum: A molecular dynamics study,” Journal of Alloys and Compounds. 2021. link Times cited: 14 USED (low confidence) Q. Pei, M. Jhon, S. Quek, and Z. Wu, “A systematic study of interatomic potentials for mechanical behaviours of Ti-Al alloys,” Computational Materials Science. 2021. link Times cited: 19 USED (low confidence) S. Wang, K. Dang, R. Mccabe, L. Capolungo, and C. Tomé, “Three-dimensional atomic scale characterization of 112¯2 twin boundaries in titanium,” Acta Materialia. 2021. link Times cited: 19 USED (low confidence) L.-F. Zhu, J. Janssen, S. Ishibashi, F. Körmann, B. Grabowski, and J. Neugebauer, “A fully automated approach to calculate the melting temperature of elemental crystals,” Computational Materials Science. 2021. link Times cited: 17 USED (low confidence) P. Li et al., “Temperature-dependent deformation processes in two-phase TiAl + Ti3Al nano-polycrystalline alloys,” Materials & Design. 2021. link Times cited: 10 USED (low confidence) D. Luan, Y.-bao Wang, G. Li, L. Yuan, and J. Chen, “The plasticity and melting characteristics of metal Al with Ti-cluster under shock loading,” Chinese Physics B. 2021. link Times cited: 0 USED (low confidence) M. He, E. T. Karim, M. Shugaev, and L. Zhigilei, “Atomistic simulation of the generation of vacancies in rapid crystallization of metals,” Acta Materialia. 2021. link Times cited: 7 USED (low confidence) H. Zhang, B. Wei, X. Ou, S. Ni, K. Zhou, and M. Song, “Dislocation Induced FCC Twins at the HCP/FCC Interfaces in a Deformed Ti-5Al Alloy: Experiments and Simulations,” Materials Science eJournal. 2020. link Times cited: 0 Abstract: This paper proposes a new formation route for the face-cente… read moreAbstract: This paper proposes a new formation route for the face-centered cubic (FCC) twins at the hexagonal close-packed (HCP)/FCC interface in a deformed Ti-5at.%Al alloy. From the experimental results, an FCC band that orients in a prismatic-type (P-type) relationship with the HCP matrix is surrounded by a group of FCC lamellae that align in parallel and orient in a basal-type (B-type) orientation relationship within the HCP matrix. The high-resolution transmission electron microscopy (HRTEM) reveals a local { } twinning relation between the FCC band and the FCC lamellae at their contacting boundaries. Molecular dynamics (MD) simulations indicate that basal stacking faults (BSFs), which later evolve into the FCC lamella in a B-type OR with the HCP matrix, initiate from the misfit regions at the relaxed P-type HCP/FCC interfaces, which then provide the nucleation source for a full dislocation that continues to slip in the initial FCC grain. Repeating these two processes produce the { } twinning relation between the new-forming FCC lamella and the initial FCC grain. The lattice correspondence analysis further interprets the formation route for the { } twins proposed in the present study from the aspect of crystal geometry. read less USED (low confidence) Z. Fan and H. Men, “A molecular dynamics study of heterogeneous nucleation in generic liquid/substrate systems with positive lattice misfit,” Materials Research Express. 2020. link Times cited: 10 Abstract: Nucleation plays a critical role in many natural and technol… read moreAbstract: Nucleation plays a critical role in many natural and technological processes, and nucleation control requires detailed understanding of nucleation process at atomic level. In this study, we investigate the atomistic mechanism of heterogeneous nucleation in generic systems of liquid/substrate with positive lattice misfit (the solid has larger atomic spacing than the substrate) using molecular dynamics (MD) simulations. We found that heterogeneous nucleation process in such systems can be best described by a 3-layer nucleation mechanism: formation of the completely ordered first layer with an epitaxial relationship with the top surface of the substrate; formation of vacancies in the second layer to accommodate lattice misfit; and creation of a nearly perfect crystal plane of the solid in the third layer that demarcates the end of nucleation and the start of crystal growth. This 3-layer nucleation process creates a 2D nucleus (a plane of the solid phase), which contrasts with the hemisphere of the solid (a 3D nucleus) in the classical nucleation theory (CNT). It is expected that this 3-layer nucleation mechanism will provide new insight for nucleation control through effective manipulation of the liquid/substrate interface. read less USED (low confidence) H. Zhang, X. Ou, S. Ni, and M. Song, “Toughening alpha-Ti by dislocation-induced phase transformation at crack tips,” Mechanics of Materials. 2020. link Times cited: 7 USED (low confidence) D. Waryoba, Z. Islam, T. Reutzel, and A. Haque, “Electro-strengthening of the additively manufactured Ti–6Al–4V alloy,” Materials Science and Engineering A-structural Materials Properties Microstructure and Processing. 2020. link Times cited: 15 USED (low confidence) T. Li et al., “Investigation of triple-coalescence behaviors for comprehensively understanding the structural evolution of coalesced TiAl droplets from an atomic-level view,” Journal of Alloys and Compounds. 2020. link Times cited: 7 USED (low confidence) S. A. Etesami, M. Laradji, and E. Asadi, “Reliability of molecular dynamics interatomic potentials for modeling of titanium in additive manufacturing processes,” Computational Materials Science. 2020. link Times cited: 5 USED (low confidence) J. Zhang et al., “Selection and mechanical evaluation of γ/γ boundary in γ-TiAl alloy,” Intermetallics. 2020. link Times cited: 7 USED (low confidence) Y. Zhang et al., “Deformation behavior and phase transformation of nanotwinned Al/Ti multilayers,” Applied Surface Science. 2020. link Times cited: 25 USED (low confidence) A. Chauniyal and R. Janisch, “Influence of lattice misfit on the deformation behaviour of α2/γ lamellae in TiAl alloys,” Materials Science and Engineering A-structural Materials Properties Microstructure and Processing. 2020. link Times cited: 11 USED (low confidence) R. Voskoboinikov, “Optimal sampling of MD simulations of primary damage formation in collision cascades,” Nuclear Instruments & Methods in Physics Research Section B-beam Interactions With Materials and Atoms. 2020. link Times cited: 5 USED (low confidence) J. Chapman and R. Ramprasad, “Nanoscale Modeling of Surface Phenomena in Aluminum Using Machine Learning Force Fields,” The Journal of Physical Chemistry C. 2020. link Times cited: 7 Abstract: The study of nano-scale surface phenomena is essential in un… read moreAbstract: The study of nano-scale surface phenomena is essential in understanding the physical processes that aid in technologically relevant applications, such as catalysis, material growth, and failure nuc... read less USED (low confidence) T. Fujinaga, Y. Watanabe, and Y. Shibuta, “Nucleation dynamics in Al solidification with Al-Ti refiners by molecular dynamics simulation,” Computational Materials Science. 2020. link Times cited: 7 USED (low confidence) S. Rawat and S. Chaturvedi, “Strain-rate effect on plasticity and ω-phase transformation in single crystal titanium: A molecular dynamics study,” Mechanics of Materials. 2020. link Times cited: 5 USED (low confidence) M. Gong, S. Xu, L. Capolungo, C. Tomé, and J. Wang, “Interactions between 〈a〉 dislocations and three-dimensional 112¯2 twin in Ti,” Acta Materialia. 2020. link Times cited: 13 USED (low confidence) H. Zhu et al., “The formation and accumulation of radiation-induced defects and the role of lamellar interfaces in radiation damage of titanium aluminum alloy irradiated with Kr-ions at room temperature,” Acta Materialia. 2020. link Times cited: 12 USED (low confidence) A. B. Patel and H. Sheng, “Structure and atomic transport of liquid titanium from a pair potential model,” Physical Review B. 2020. link Times cited: 1 USED (low confidence) W. Li et al., “Understanding the atomistic deformation mechanisms of polycrystalline γ-TiAl under nanoindentation: Effect of lamellar structure,” Journal of Alloys and Compounds. 2020. link Times cited: 16 USED (low confidence) M. Daly, A. Kumar, C. V. Singh, and G. Hibbard, “On the competition between nucleation and thickening in deformation twinning of face-centered cubic metals,” International Journal of Plasticity. 2020. link Times cited: 8 USED (low confidence) X. Liu, L. Xu, and S. Zhang, “Molecular dynamics simulation of Ti-6AL-4V diffusion bonding behavior under different process parameters,” Materiali in Tehnologije. 2020. link Times cited: 2 Abstract: In this paper the diffusion-bonding process of a titanium al… read moreAbstract: In this paper the diffusion-bonding process of a titanium alloy was investigated in detail using molecular dynamics. The protocell model of a Ti-6Al-4V alloy was obtained by the atomic random substitution method. The mixed potential function method, EAM (Embedded Atom Method) and Morse potential was used to deal with the Ti-Al-V ternary alloy system. And the diffusion bonding process of Ti-6Al-4V was simulated numerically. The influence of temperature, pressure and holding time on the diffusion bonding behavior of Ti-6Al-4V alloys was studied. The results showed that an increase of the temperature, pressure and holding time can improve the diffusion of interfacial atoms and increase the diffusion bonding width. In addition, the diffusion temperature has a critical value, i.e., 1100 K. When the temperature is lower than 1100 K, the interface atoms hardly diffuse. The MSD (Mean Square Deviation) vs. t curves of Ti, Al and V atoms at different temperatures were established. The diffusion coefficients of Ti, Al and V atoms at different temperatures were obtained by the relationship between the MSD and the atomic diffusion coefficient, after which the Arrhenius equations of the diffusion coefficient were obtained, respectively. Based on the diffusion coefficient equation, the diffusion activation energies of each element were deduced. Compared with the experimental data, the rationality of the simulation results was verified. read less USED (low confidence) S. Surulere, M. Shatalov, A. C. Mkolesia, and A. Adeniji, “A Comparative Investigation of Complex Conjugate Eigenvalues of Generalized Morse and Classical Lennard-Jones Potential for Metal Atoms.” 2020. link Times cited: 0 Abstract:
The knowledge of parameter estimation for interatomic pote… read moreAbstract:
The knowledge of parameter estimation for interatomic potentials is
useful in the computation of the vibrational structure of van der Waals molecules.
On the estimation of the Generalized Morse and Classical Lennard-Jones potential
energy functions, complex conjugates eigenvalues may be obtained. Different approaches can be
used to solve this resulting problem. A method that uses the objective least squares function
method to estimate parameters of the interatomic potentials is employed.
Numerical simulation of the systems using metal atoms yields complex conjugates eigenvalues
at some initial point.
Other approaches of solving the complex conjugates eigenvalues problem are discussed
comprehensively.
read less USED (low confidence) N. Kaur, C. Deng, and O. Ojo, “Effect of solute segregation on diffusion induced grain boundary migration studied by molecular dynamics simulations,” Computational Materials Science. 2020. link Times cited: 12 USED (low confidence) T. Fujinaga and Y. Shibuta, “Molecular dynamics simulation of heterogeneous nucleation from concave cavity at surface of grain refiner,” IOP Conference Series: Materials Science and Engineering. 2020. link Times cited: 1 Abstract: Grain refiners are often used in practical production proces… read moreAbstract: Grain refiners are often used in practical production processes of metallic materials to promote and control nucleation. Although morphology of the grain refiner strongly affects nucleation behaviour, it is not well understood how unevenness of surface of the grain refiner affects nucleation from atomistic viewpoint. In this study, effect of concave cavity at surface of the grain refiner on heterogeneous nucleation is investigated by molecular dynamics (MD) simulation. HCP-Ti cube with a concave cavity is employed in the MD simulation as a grain refiner of the solidification of undercooled Al melt as a model study. HCP-Al solid is firstly formed at the tip or on the side wall of cavity and FCC-Al growth is followed on the exposed (0001) surface of HCP-Al for most of the cavities, whereas FCC-Al solid is directly formed on HCP(0001) terraces at the side wall of the cavity with large-obtuse apex angle. read less USED (low confidence) J. Wang, W. Oates, and R. Kumar, “Material Characterization of a Flat Plate with Shock Impingement: from Continuum to Atomistic Scale,” AIAA AVIATION 2020 FORUM. 2020. link Times cited: 0 USED (low confidence) Y.-chun Huang, K. Zhao, Y. Liu, X. Zhang, H. Du, and X. Ren, “Investigation on adsorption of Ar and N2 on α-Al2O3(0001) surface from first-principles calculations,” Vacuum. 2020. link Times cited: 10 USED (low confidence) A. Lungidningtyas and A. A. Parikesit, “In Silico Analysis of Ethanol Binding Activity in Neuronal Nicotinic Acetylcholine Receptors.” 2020. link Times cited: 2 Abstract: Ethanol and nicotine are two common substances that are ofte… read moreAbstract: Ethanol and nicotine are two common substances that are often linked to complications in alcoholic smokers. The high number of the co-consumptions in alcoholic smokers suggested a possible interaction between ethanol and nicotine in the central nervous system and a potential similar mechanism of action. Both ethanol and nicotine are shown to bind with neuronal nicotinic acetylcholine receptors (nAChRs), a ligand gated cation channel specifically targeted by the endogenous acetylcholine. Ethanol has a much less specific binding capability to modulate the receptors, however, emerging reports indicates that ethanol can interact with nAChRs both directly and indirectly. This study focuses on the analysis of ethanol binding sites with nAChRs using molecular docking techniques obtained from the Protein Data Bank. The obtained data showed a possible binding site for ethanol in nAChRs, however, upon validation, result is not substantial. Nevertheless, the obtained data should be useful for future reference for the basis of ethanol interactions with the human nAChRs proteins. read less USED (low confidence) Q. Zu, Y.-F. Guo, and X. Yao, “Surface and orientation effects on stress-induced hcp-fcc phase transformation in Ti nanopillars,” Applied Surface Science. 2020. link Times cited: 9 USED (low confidence) H. Fan, Q. Wang, J. El-Awady, D. Raabe, and M. Zaiser, “Strain rate dependency of dislocation plasticity,” Nature Communications. 2020. link Times cited: 125 USED (low confidence) J. Chen, W. Chen, S. Chen, G. Zhou, and T. Zhang, “Shock Hugoniot and Mie-Grüneisen EOS of TiAl alloy: A molecular dynamics approach,” Computational Materials Science. 2020. link Times cited: 9 USED (low confidence) B. Zhao, P. Huang, L. Zhang, S. Li, Z. Zhang, and Q. Yu, “Temperature Effect on Stacking Fault Energy and Deformation Mechanisms in Titanium and Titanium-aluminium Alloy,” Scientific Reports. 2020. link Times cited: 32 USED (low confidence) C. Cheng et al., “Development and application of EAM potentials for Ti, Al and Nb with enhanced planar fault energy of Ti,” Computational Materials Science. 2020. link Times cited: 4 USED (low confidence) K. Dang, D. Bamney, L. Capolungo, and D. Spearot, “Mobility of dislocations in aluminum: The role of non-Schmid stress state,” Acta Materialia. 2020. link Times cited: 16 USED (low confidence) H. Zhang, X. Ou, B. Wei, S. Ni, and M. Song, “Strain direction dependency of deformation mechanisms in an HCP-Ti crystalline by molecular dynamics simulations,” Computational Materials Science. 2020. link Times cited: 25 USED (low confidence) W. Li et al., “Effects of γ/γ interfaces in TiAl lamellae subjected to uniaxial tensile loading,” Computational Materials Science. 2020. link Times cited: 11 USED (low confidence) G. Plummer and G. Tucker, “Bond-order potentials for theTi3AlC2andTi3SiC2MAX phases,” Physical Review B. 2019. link Times cited: 12 USED (low confidence) C. Ebner, J. Rajagopalan, C. E. Lekka, and C. Rentenberger, “Electron beam induced rejuvenation in a metallic glass film during in-situ TEM tensile straining,” Acta Materialia. 2019. link Times cited: 7 USED (low confidence) R. Voskoboinikov, “An MD study of primary damage formation in aluminium,” Nuclear Instruments & Methods in Physics Research Section B-beam Interactions With Materials and Atoms. 2019. link Times cited: 7 USED (low confidence) R. Voskoboinikov, “A contribution of L10 ordered crystal structure to the high radiation tolerance of γ-TiAl intermetallics,” Nuclear Instruments & Methods in Physics Research Section B-beam Interactions With Materials and Atoms. 2019. link Times cited: 9 USED (low confidence) V. Jordan and I. Shmakov, “The influence of the ignition conditions of the SH-synthesis of intermetallic compounds on the combustion parameters of the Ti-15.82wt.%Al composition: computer simulation and computing experiments,” Journal of Physics: Conference Series. 2019. link Times cited: 0 Abstract: Computational experiments (CEs) have been carried out to sim… read moreAbstract: Computational experiments (CEs) have been carried out to simulate the propagation of the combustion wave of the SH-synthesis process in a package of alternating layers of nanoscale crystal lattices of Ti and Al atoms by molecular dynamics method. The interatomic interaction potential in the embedded atom model (EAM) was used in the LAMMPS package. Using the LAMMPS configuration with parallel computing, the following results of CEs were obtained: sets of temperature profiles along the layers of the structure at successive instants of time (up to 16 ns) and the corresponding sets of snapshots (vertical cross-sections of the atomic arrangement along the layers), as well as a tables with the number and percentage of the content of various types of elementary cells (fcc, hcp, bcc, other) at the same instants of time. The influence of the initiation’s conditions of the SH-synthesis of intermetallic compounds on the combustion parameters of the nanoscale layered Ti-15.82wt.%Al composition was showed. The ignition conditions of SHS that are provided the stable motion of the combustion wave in the SHS-sample were determined. And the ignition conditions of SHS with dominance of either TiAl or Ti3Al phase formation in the SHS products was also determined. read less USED (low confidence) V. Jordan and I. Shmakov, “The emergence of a heterostructure of the intermetallic phases in the process of SH-synthesis simulation in a nonstoichiometric nanoscale layered Ti-Al system,” Journal of Physics: Conference Series. 2019. link Times cited: 1 Abstract: Computational experiments (CEs) have been carried out to sim… read moreAbstract: Computational experiments (CEs) have been carried out to simulate the propagation of the combustion wave of the SH-synthesis process in a package of alternating nanosized layers of crystal lattices of Ti and Al atoms by the «molecular dynamics» method. By means the LAMMPS package performing parallel computing the computational experiments (CEs) have been carried out. The “embedded atom” model (EAM) for the interatomic interaction potential was used. The two structures of Ti-Al system with various quantities of atoms and nonstoichiometric ratios have been studied. The sets of temperature and density profiles along the layered structure at successive instants of time (up to 16 ns) have been calculated. In addition, the corresponding sets of vertical cross-sections of the distributions of atoms and various types of elementary cells (fcc, hcp, bcc, etc.) have been calculated. The emergence of heterostructure of intermetallic phases in the Ti-Al system with 453974 atoms and the nonstoichiometric ratio of 1.23 has been detected. read less USED (low confidence) D. Nguyen-Trong, K. Pham-Huu, and P. Nguyen-Tri, “Simulation on the Factors Affecting the Crystallization Process of FeNi Alloy by Molecular Dynamics,” ACS Omega. 2019. link Times cited: 24 Abstract: This paper investigates the crystallization process of FeNi … read moreAbstract: This paper investigates the crystallization process of FeNi alloys with different impurity concentrations of Ni(x) [x = 10% (Fe90Ni10), 20% (Fe80Ni20), 30% (Fe70Ni30), 40% (Fe60Ni40), and 50% (Fe50Ni50)] at temperature (T) = 300 K and Fe70Ni30 at heating rates of 4 × 1012, 4 × 1013, and 4 × 1014 K/s at different temperatures, T = 300, 400, 500, 600, 700, 900, 1100, and 1300 K. Molecular dynamics models with the Sutton–Chen embedded interaction potential and recirculating boundary conditions are used to calculate the molecular parameters of alloys, such as radial distribution function, total energy of the system (Etot), size (l), and crystallization temperature (through the relationship between Etot and T). The common neighborhood analysis method is used to confirm the theoretical results of crystallization for Fe–Fe, Fe–Ni, and Ni–Ni. The annealing process did not have an effect on the crystallization process of FeNi alloys. The effect of Ni content, heating rate, and annealing time on structural unit numbers, such as face-centered cubic, hexagonal close-packed, blocked cubic center, and amorphous, and the crystallization process of FeNi alloys is also investigated. read less USED (low confidence) A. Mayer and P. N. Mayer, “Evolution of pore ensemble in solid and molten aluminum under dynamic tensile fracture: Molecular dynamics simulations and mechanical models,” International Journal of Mechanical Sciences. 2019. link Times cited: 35 USED (low confidence) A. Yang, M. Qiu, J. Cui, Q. Hou, and B. Fu, “Effects of temperature and surface orientation on migration behaviors of helium atoms near titanium surfaces,” Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms. 2019. link Times cited: 2 USED (low confidence) P. N. Mayer and A. Mayer, “Statistical Distribution of Pores in Solid and Molten Metals at Dynamic Tensile Fracture,” Structural Integrity. 2019. link Times cited: 0 USED (low confidence) T. Fujinaga and Y. Shibuta, “Molecular dynamics simulation of athermal heterogeneous nucleation of solidification,” Computational Materials Science. 2019. link Times cited: 20 USED (low confidence) H. Zhu et al., “Atomic origins of radiation-induced defects and the role of lamellar interfaces in radiation damage of titanium aluminide alloy irradiated with Kr-ions at elevated temperature,” Acta Materialia. 2019. link Times cited: 13 USED (low confidence) P. Chen, F. Wang, and B. Li, “Transitory phase transformations during 101¯2 twinning in titanium,” Acta Materialia. 2019. link Times cited: 41 USED (low confidence) P. Zhao et al., “Slip transmission assisted by Shockley partials across α/β interfaces in Ti-alloys,” Acta Materialia. 2019. link Times cited: 22 USED (low confidence) R. Voskoboinikov, “An insight into radiation resistance of D019 Ti3Al intermetallics,” Journal of Nuclear Materials. 2019. link Times cited: 15 USED (low confidence) W. Li et al., “Atomistic simulation of crack propagation along γ-TiAl lamellar interface,” IOP Conference Series: Materials Science and Engineering. 2019. link Times cited: 2 Abstract: Due to start-up and shut-down operations of engine, TiAl str… read moreAbstract: Due to start-up and shut-down operations of engine, TiAl structural components usually undergo not only static but also cyclic mechanical loading. The crack propagation mechanisms of γ-TiAl under two types of loading are studied in this work to reveal the differences of the mechanisms under constant strain rate and cyclic loading. Since the crack prefers to nucleate at the interface, two types of loadings are applied to a γ-TiAl interface system with a pre-existing micro-crack at the interface by the means of classical molecular dynamics simulation, the loading direction is along [111] perpendicular to the interface. The evolution of crack tip and dislocation is observed in atomistic scale. The results show that, under both loading types, the crack propagates asymmetrically, Shockley dislocations emit on the (-1-11) slip plane from the right crack tip and slip along [-1-1-2] direction. The dislocations blunt the extension of crack while the left crack tip propagates in a brittle way. During the cyclic loading, different with constant strain rate condition, the crack advances and dislocations slip with increasing loads and retreat during unloading. In addition, the stress decreases and the crack length increases with the increase of the cyclic loading number. read less USED (low confidence) J. Fürnkranz, “Publication list,” Journal of Physics: Conference Series. 2019. link Times cited: 10 Abstract: PUBLICATION LIST of VICTOR MANUEL VILLANUEVA SANDOVAL availa… read moreAbstract: PUBLICATION LIST of VICTOR MANUEL VILLANUEVA SANDOVAL available in this PDF. read less USED (low confidence) H. Hu, Y. Ren, X. Wu, W. Liu, and J. J. Luo, “First-principles calculations of the site preference, phase stability and brittle versus ductile behaviors of TiAl intermetallic alloyed with ternary elements,” International Journal of Modern Physics B. 2019. link Times cited: 3 Abstract: Effects of site preference, phase stability and brittle vers… read moreAbstract: Effects of site preference, phase stability and brittle versus ductile behaviors of W, Mo, La and Ce in TiAl have been investigated by using the first-principles calculations. The results show that transition elements W and Mo can effectively stabilize B2 phase except rare earth elements La or Ce. Elastic modulus show that the ductility can be improved for ternary elements addition and there is a plastic transition from intrinsic brittleness to intrinsic ductility with W and Mo addition due to phase transition. The competitive mechanisms between the opening of microcracks and dislocation emission show the increased ductility is mainly due to the energetic dislocation but suppressed cracks. Finally, electronic density of states and charge density show that weakened covalent interactions of TiAl for W, Mo, La and Ce addition are the essential reasons for the transformation from brittleness to ductility. read less USED (low confidence) K. Dang, D. Bamney, K. Bootsita, L. Capolungo, and D. Spearot, “Mobility of dislocations in Aluminum: Faceting and asymmetry during nanoscale dislocation shear loop expansion,” Acta Materialia. 2019. link Times cited: 33 USED (low confidence) H. Zhu et al., “Atomic Origins of Radiation-Induced Defects and Interfacial Strengthening in Additively Manufactured Titanium Aluminide Alloy Irradiated with Kr-Ions at Elevated Temperature,” MatSciRN: Process & Device Modeling (Topic). 2019. link Times cited: 0 Abstract: The irradiation microstructure of the additively manufacture… read moreAbstract: The irradiation microstructure of the additively manufactured titanium aluminide (TiAl) alloy subjected to in situ transmission electron microscope (TEM) irradiation with 1 MeV Kr ions at the elevated temperature of 873K was investigated. Triangle and large hexagon shaped volume defects were observed within the γ-TiAl phase in the TEM images of the irradiated microstructure. High resolution TEM images and composition analyses revealed the volume defects were vacancy-type stacking fault tetrahedrals (SFTs). Molecular dynamic simulations showed that the increased diffusion coefficient at the elevated temperature promoted the movement and aggregation of vacancies, leading to the formation and growth of SFTs in the irradiated FCC γ phase. The lamellar interfaces in the irradiation microstructure were more effective for acting as strong sinks to absorb the primary point defects and defect clusters at the elevated temperature. The initial defects at the interfaces of the additively manufactured TiAl alloy enhanced the sink strength of the material and greatly refined SFTs near the lamellar interfaces. read less USED (low confidence) H. Bhattarai, K. E. Newman, and J. Gezelter, “Polarizable potentials for metals: The density readjusting embedded atom method (DR-EAM),” Physical Review B. 2019. link Times cited: 6 Abstract: In simulations of metallic interfaces, a critical aspect of … read moreAbstract: In simulations of metallic interfaces, a critical aspect of metallic behavior is missing from the some of the most widely used classical molecular dynamics force fields. We present a modification of the embedded atom method (EAM) which allows for electronic polarization of the metal by treating the valence density around each atom as a fluctuating dynamical quantity. The densities are represented by a set of additional fluctuating variables (and their conjugate momenta) which are propagated along with the nuclear coordinates. This ``density readjusting EAM'' (DR-EAM) preserves nearly all of the useful qualities of traditional EAM, including bulk elastic properties and surface energies. However, it also allows valence electron density to migrate through the metal in response to external perturbations. We show that DR-EAM can successfully model polarization in response to external charges, capturing the image charge effect in atomistic simulations. DR-EAM also captures some of the behavior of metals in the presence of uniform electric fields, predicting surface charging and shielding internal to the metal. We further show that it predicts charge transfer between the constituent atoms in alloys, leading to novel predictions about unit cell geometries in layered $\mathrm{L}{1}_{0}$ structures. read less USED (low confidence) X. Zheng et al., “Deformation induced FCC lamellae and their interaction in commercial pure Ti,” Scripta Materialia. 2019. link Times cited: 62 USED (low confidence) W. Li et al., “Tensile behavior of γ/α2 interface system in lamellar TiAl alloy via molecular dynamics,” Computational Materials Science. 2019. link Times cited: 19 USED (low confidence) J. Ding et al., “Micro-mechanism of the effect of grain size and temperature on the mechanical properties of polycrystalline TiAl,” Computational Materials Science. 2019. link Times cited: 23 USED (low confidence) M. Gong et al., “Steps and 112¯1 secondary twinning associated with 112¯2 twin in titanium,” Acta Materialia. 2019. link Times cited: 27 USED (low confidence) D. Qiu et al., “Predicting grain boundary structure and energy in BCC metals by integrated atomistic and phase-field modeling,” Acta Materialia. 2019. link Times cited: 18 USED (low confidence) J. Chapman, R. Batra, B. Uberuaga, G. Pilania, and R. Ramprasad, “A comprehensive computational study of adatom diffusion on the aluminum (1 0 0) surface,” Computational Materials Science. 2019. link Times cited: 9 USED (low confidence) S. A. Etesami, M. Laradji, and E. Asadi, “Transferability of interatomic potentials in predicting the temperature dependency of elastic constants for titanium, zirconium and magnesium,” Modelling and Simulation in Materials Science and Engineering. 2019. link Times cited: 4 Abstract: We present our investigation of the current state of the art… read moreAbstract: We present our investigation of the current state of the art for the transferability of molecular dynamics (MD) interatomic potentials for high temperature simulations of material processes in terms of elastic constants. With the current advancement of computer power, nanoscale computational models such as MD have the potential to accelerate optimization and development of high temperature material processes provided a robust and transferable interatomic potential. Temperature dependency of elastic constants, despite the low temperature elastic constants, is not commonly used as one of the target material properties to develop interatomic potentials for metals; thus, it is a reliable index to determine the transferability of interatomic potentials for high temperature simulations. We consider all five independent elastic constants and their temperature dependency as an index for our evaluations of available interatomic potentials for titanium (Ti), zirconium (Zr), and magnesium (Mg) as representative metals with a relatively complex crystal structure (hcp). The calculated elastic constants and their deviation from their corresponding experimental values are presented. We provide a through discussion on the transferability of each potential and summarize with the most suitable potentials for high temperature material process simulations for each considered material. read less USED (low confidence) M. Dupraz, S. Rao, and H. V. Swygenhoven, “Large Scale 3-Dimensional Atomistic Simulations of Screw Dislocations Interacting with Coherent Twin Boundaries in Al, Cu and Ni Under Uniaxial and Multiaxial Loading Conditions,” MatSciRN: Process & Device Modeling (Topic). 2019. link Times cited: 17 USED (low confidence) X. Y. Wang, S. Zhang, S. Feng, L. Qi, and R. Liu, “Effect of pressure on the structure of Ti75Al25 alloy during rapid-quenching process,” Journal of Non-Crystalline Solids. 2018. link Times cited: 6 USED (low confidence) E. Dolgusheva, “Thermal properties of fcc titanium and aluminum thin films,” Computational Materials Science. 2018. link Times cited: 3 USED (low confidence) P. N. Mayer and A. Mayer, “Size distribution of pores in metal melts at non-equilibrium cavitation and further stretching, and similarity with the spall fracture of solids,” International Journal of Heat and Mass Transfer. 2018. link Times cited: 18 USED (low confidence) H. N. Pishkenari, F. S. Yousefi, and A. Taghibakhshi, “Determination of surface properties and elastic constants of FCC metals: a comparison among different EAM potentials in thin film and bulk scale,” Materials Research Express. 2018. link Times cited: 22 Abstract: Three independent elastic constants C11, C12, and C44 were c… read moreAbstract: Three independent elastic constants C11, C12, and C44 were calculated and compared using available potentials of eight different metals with FCC crystal structure; Gold, Silver, Copper, Nickel, Platinum, Palladium, Aluminum and Lead. In order to calculate the elastic constants, the second derivative of the energy density of each system was calculated with respect to different directions of strains. Each set of the elastic constants of the metals in bulk scale was compared with experimental results, and the average relative error was for each was calculated and compared with other available potentials. Then, using the Voigt-Reuss-Hill method, approximated values for Young and shear moduli and Poisson’s ratio of the FCC metals in the bulk scale were found for each potential. Furthermore, to observe the surface effects on the metals in nanoscale, surface elastic constants of the thin films of the metals have been calculated. In the study of the thin films of materials in nanoscale, the number of surface atoms is considerable compared to all atoms of the object. This leads to an increase in the surface effects, which influence the elastic properties. By considering this fact and employing related definitions and equations, the properties of the thin films of the metals were calculated, and the surface effects for different crystallographic directions were compared. Subsequently, in some cases, comparisons among characteristics of the metals in the thin film and bulk material were made. read less USED (low confidence) V. Iacobellis, A. Radhi, and K. Behdinan, “A bridging cell multiscale modeling of carbon nanotube-reinforced aluminum nanocomposites,” Composite Structures. 2018. link Times cited: 23 USED (low confidence) J. Harrison, J. Schall, S. Maskey, P. Mikulski, M. T. Knippenberg, and B. Morrow, “Review of force fields and intermolecular potentials used in atomistic computational materials research,” Applied Physics Reviews. 2018. link Times cited: 99 Abstract: Molecular simulation is a powerful computational tool for a … read moreAbstract: Molecular simulation is a powerful computational tool for a broad range of applications including the examination of materials properties and accelerating drug discovery. At the heart of molecular simulation is the analytic potential energy function. These functions span the range of complexity from very simple functions used to model generic phenomena to complex functions designed to model chemical reactions. The complexity of the mathematical function impacts the computational speed and is typically linked to the accuracy of the results obtained from simulations that utilize the function. One approach to improving accuracy is to simply add more parameters and additional complexity to the analytic function. This approach is typically used in non-reactive force fields where the functional form is not derived from quantum mechanical principles. The form of other types of potentials, such as the bond-order potentials, is based on quantum mechanics and has led to varying levels of accuracy and transferability. When selecting a potential energy function for use in molecular simulations, the accuracy, transferability, and computational speed must all be considered. In this focused review, some of the more commonly used potential energy functions for molecular simulations are reviewed with an eye toward presenting their general forms, strengths, and weaknesses.Molecular simulation is a powerful computational tool for a broad range of applications including the examination of materials properties and accelerating drug discovery. At the heart of molecular simulation is the analytic potential energy function. These functions span the range of complexity from very simple functions used to model generic phenomena to complex functions designed to model chemical reactions. The complexity of the mathematical function impacts the computational speed and is typically linked to the accuracy of the results obtained from simulations that utilize the function. One approach to improving accuracy is to simply add more parameters and additional complexity to the analytic function. This approach is typically used in non-reactive force fields where the functional form is not derived from quantum mechanical principles. The form of other types of potentials, such as the bond-order potentials, is based on quantum mechanics and has led to varying levels of accuracy and transferabilit... read less USED (low confidence) R. Babu, K. Vamsi, and S. Karthikeyan, “On the formation and stability of precipitate phases in a near lamellar γ-TiAl based alloy during creep,” Intermetallics. 2018. link Times cited: 13 USED (low confidence) N. Dũng, “Influence of impurity concentration, atomic number, temperature and tempering time on microstructure and phase transformation of Ni1−xFex (x = 0.1, 0.3, 0.5) nanoparticles,” Modern Physics Letters B. 2018. link Times cited: 17 Abstract: The influence of the concentration of impurity Fe in nanopar… read moreAbstract: The influence of the concentration of impurity Fe in nanoparticles Ni1−xFex with x = 0.1, 0.3 and 0.5 at T = 300 K; 4000 atoms, 5324 atoms, 6912 atoms and 8788 atoms at T = 300 K; 6912 atoms at T =... read less USED (low confidence) G. Förster and L. J. Lewis, “Numerical study of double-pulse laser ablation of Al,” Physical Review B. 2018. link Times cited: 15 USED (low confidence) P. Liu, X. Han, D. Sun, and Q. Wang, “Development and application of a ternary Ti-Al-N interatomic potential for Ti2AlN/TiAl composite,” Journal of Alloys and Compounds. 2018. link Times cited: 20 USED (low confidence) D. Chakraborty, A. Harms, M. A. Ullah, W. J. Weber, and D. Aidhy, “Effect of atomic order/disorder on vacancy clustering in concentrated NiFe alloys,” Computational Materials Science. 2018. link Times cited: 7 USED (low confidence) B. Jeong, J. Kim, T. Lee, S.-W. Kim, and S. Ryu, “Systematic investigation of the deformation mechanisms of a γ-TiAl single crystal,” Scientific Reports. 2018. link Times cited: 25 USED (low confidence) Y. Gao, M. Takahashi, C. Cavallotti, and G. Raos, “Molecular dynamics simulation of metallic impurity diffusion in liquid lead-bismuth eutectic (LBE),” Journal of Nuclear Materials. 2018. link Times cited: 13 USED (low confidence) M. Tahiri, A. Hasnaoui, and K. Sbiaai, “Atomic Scale Investigation of Structural Properties and Glass Forming Ability of Ti100−xAlx Metallic Glasses,” Metallurgical and Materials Transactions A. 2018. link Times cited: 7 USED (low confidence) M. Tahiri, A. Hassani, K. Sbiaai, and A. Hasnaoui, “Investigating local atomic structural order in TiAl3 metallic glass using molecular dynamic simulation,” Computational Condensed Matter. 2018. link Times cited: 8 USED (low confidence) D. S. Kanibolotsky, U. K. U. A. V. Blvd., O. Shcheretskyi, M. V. Afanasiev, and A. Verkhovliuk, “Modelling of Structure of a Liquid Al–0.2% Ti Alloy,” Metallofizika I Noveishie Tekhnologii. 2018. link Times cited: 0 USED (low confidence) X. Chen, S. Lu, Z. Yang, T. Fu, C. Huang, and X. Peng, “Molecular dynamic simulation on nano-indentation of NiTi SMA,” Materials Science and Engineering A-structural Materials Properties Microstructure and Processing. 2018. link Times cited: 41 USED (low confidence) Y. He et al., “Dislocation dipole-induced strengthening in intermetallic TiAl,” Scripta Materialia. 2018. link Times cited: 17 USED (low confidence) S. Kiselev, N. Ryashin, E. A. Maximovsky, V. Kiselev, A. Filippov, and A. Polukhin, “Simulation of Ti-Al intermetallic compound synthesis using cold spraying.” 2017. link Times cited: 0 Abstract: The results of the experiment and numerical simulation of Ti… read moreAbstract: The results of the experiment and numerical simulation of Ti-Al intermetallic compound synthesis using cold gas-dynamic spraying and heat postprocessing in an oven at a temperature above the aluminum melting temperature are presented. Ti-Al-type intermetallic systems were obtained at heating temperatures from 930 to 1620 K and phase composition and crystal structure of the compounds were studied. Numerical simulation of the intermetallic synthesis process performed by the molecular dynamics method had shown that the kinetics of the process at these temperatures is determined by the diffusion and dissolution processes of titanium in molten aluminum. read less USED (low confidence) R. Babicheva et al., “Effect of grain boundary segregation of Co or Ti on cyclic deformation of aluminium bi-crystals,” International Journal of Fatigue. 2017. link Times cited: 23 USED (low confidence) S. Tang, G. Zhang, N. Zhou, T. Guo, and X. Huang, “Uniaxial stress-driven grain boundary migration in Hexagonal Close-packed (HCP) metals: Theory and MD simulations,” International Journal of Plasticity. 2017. link Times cited: 15 USED (low confidence) B. Wang, G. Kang, Q. Kan, K. Zhou, and C. Yu, “Molecular dynamics simulations to the pseudo-elasticity of NiTi shape memory alloy nano-pillar subjected to cyclic compression,” Computational Materials Science. 2017. link Times cited: 24 USED (low confidence) L.-J. Zhang, T. I. Spiridonova, S. Kulkova, R. Yang, and Q. Hu, “Atomic self-diffusion anisotropy of HCP metals from first-principles calculations,” Computational Materials Science. 2017. link Times cited: 10 USED (low confidence) I. Novoselov and A. Yanilkin, “Quantum molecular dynamics: Accelerating diffusion via parallel replica method.,” Computational Materials Science. 2017. link Times cited: 3 USED (low confidence) K. Mackenchery and A. Dongare, “Shock Hugoniot behavior of single crystal titanium using atomistic simulations.” 2017. link Times cited: 4 Abstract: Atomistic shock simulations are performed for single crystal… read moreAbstract: Atomistic shock simulations are performed for single crystal titanium using four different interatomic potentials at impact velocities ranging from 0.5 km/s to 2.0 km/s. These potentials comprise of three parameterizations in the formulation of the embedded atom method and one formulation of the modified embedded atom method. The capability of the potentials to model the shock deformation and failure behavior is investigated by computing the shock hugoniot response of titanium and comparing to existing experimental data. In addition, the capability to reproduce the shock induced alpha (α) to omega (ω) phase transformation seen in Ti is investigated. The shock wave structure is discussed and the velocities for the elastic, plastic and the α-ω phase transformation waves are calculated for all the interatomic potentials considered. read less USED (low confidence) H. Wu, D. Xu, H. Wang, and R. Yang, “Molecular Dynamics Simulation of Tensile Deformation and Fracture of γ-TiAl with and without Surface Defects,” Journal of Materials Science & Technology. 2016. link Times cited: 41 USED (low confidence) V. V. Pogorelko and A. Mayer, “Tensile strength of Al matrix with nanoscale Cu, Ti and Mg inclusions,” Journal of Physics: Conference Series. 2016. link Times cited: 5 Abstract: Molecular-dynamic investigations of Al+Cu, Al+Ti and Al+Mg n… read moreAbstract: Molecular-dynamic investigations of Al+Cu, Al+Ti and Al+Mg nanocomposite strength under high-rate uniaxial tension were carried out in this work. We consider two different mechanisms of reduction of the tensile strength of a material with inclusions in comparison with a pure material of matrix. The first mechanism is connected with a stress concentration in matrix near a stiff and strong inclusion (Ti, Cu); in this case, the fracture occurs inside the matrix and does not touch the inclusion. The second mechanism acts in the case of a soft and weak inclusion (Mg); the fracture begins inside the inclusion and thereafter propagates into the matrix. The tensile strength of the systems is determined at varied strain rates (in the range from 0.1/ns to 30/ns at the temperature 300 K) and varied temperatures (in the range from 300 K to 900 K at the strain rate 1/ns). read less USED (low confidence) S. Kiselev and N. Ryashin, “Ti-Al intermetallic compounds synthesis in coatings deposited by cold spraying.” 2016. link Times cited: 4 Abstract: In the present study Ti-Al compounds formation in cold spray… read moreAbstract: In the present study Ti-Al compounds formation in cold spray aluminium coatings on titanium alloy substrates by annealing in argon atmosphere at temperature in the range from 830 to 1270 K was considered. Experimental and modeling results of intermetallic compounds synthesis in cold spray coatings were presented. Formation of TiAl3 and Ti3Al phases was obtained. Data of X-ray, microstructure and microhardness analysis was shown. read less USED (low confidence) K. Chatterjee et al., “Study of grain-level deformation and residual stresses in Ti-7Al under combined bending and tension using high energy diffraction microscopy (HEDM),” International Journal of Solids and Structures. 2016. link Times cited: 59 USED (low confidence) M. Tahiri, S. Trady, A. Hasnaoui, M. Mazroui, K. Saadouni, and K. Sbiaai, “Structural properties of Al and TiAl3 metallic glasses — An embedded atom method study,” Modern Physics Letters B. 2016. link Times cited: 15 Abstract: In this paper, we investigated the structural properties of … read moreAbstract: In this paper, we investigated the structural properties of metallic glasses (MGs). We emphasized our study on monatomic Al and binary TiAl3 systems. The calculations are performed by using the molecular dynamics (MD) simulation based on semi-empirical many-body potentials derived from the embedded atom method. The structure is analyzed using the radial distribution function (RDF), the common neighbor analysis (CNA) and the coordination numbers (CNs). Our results demonstrated that it is possible to form MGs in both systems upon fast cooling from the liquid state. This is confirmed by the fact that the system energy and/or volume during the cooling stage decrease continuously with a slight change and by atomic scale analysis using the RDF, CNA and CN analyzing techniques. Furthermore, this specific study shows that under the same conditions, the icosahedral structures appeared in TiAl3 are more abundant than in pure Al. Implications of these findings are discussed. read less USED (low confidence) Y.-K. Kim, H. Kim, W. Jung, and B.-J. Lee, “Atomistic modeling of the Ti–Al binary system,” Computational Materials Science. 2016. link Times cited: 45 USED (low confidence) P. Tang, G. Huang, Q. Xie, J. Huang, and F. Ning, “Elastic anisotropy and phonon focusing for tetragonal crystals: Application to γ-TiAl,” Computational Materials Science. 2016. link Times cited: 8 USED (low confidence) S. M. Rassoulinejad-Mousavi, Y. Mao, and Y. Zhang, “Evaluation of Copper, Aluminum and Nickel Interatomic Potentials on Predicting the Elastic Properties,” arXiv: Computational Physics. 2016. link Times cited: 63 Abstract: Choice of appropriate force field is one of the main concern… read moreAbstract: Choice of appropriate force field is one of the main concerns of any atomistic simulation that needs to be seriously considered in order to yield reliable results. Since, investigations on mechanical behavior of materials at micro/nanoscale has been becoming much more widespread, it is necessary to determine an adequate potential which accurately models the interaction of the atoms for desired applications. In this framework, reliability of multiple embedded atom method based interatomic potentials for predicting the elastic properties was investigated. Assessments were carried out for different copper, aluminum and nickel interatomic potentials at room temperature which is considered as the most applicable case. Examined force fields for the three species were taken from online repositories of National Institute of Standards and Technology (NIST), as well as the Sandia National Laboratories, the LAMMPS database. Using molecular dynamic simulations, the three independent elastic constants, C11, C12 and C44 were found for Cu, Al and Ni cubic single crystals. Voigt-Reuss-Hill approximation was then implemented to convert elastic constants of the single crystals into isotropic polycrystalline elastic moduli including Bulk, Shear and Young's modulus as well as Poisson's ratio. Simulation results from massive molecular dynamic were compared with available experimental data in the literature to justify the robustness of each potential for each species. Eventually, accurate interatomic potentials have been recommended for finding each of the elastic properties of the pure species. Exactitude of the elastic properties was found to be sensitive to the choice of the force fields. Those potentials were fitted for a specific compound may not necessarily work accurately for all the existing pure species. read less USED (low confidence) H. Wang et al., “316. Grain Boundary-Mediated Lattice Reorientation in α-Titanium to Promote Plastic Deformation in Hard-Oriented Grains.” 2016. link Times cited: 1 USED (low confidence) A. Ready, A. Sutton, P. Haynes, and D. Rugg, “Point, Linear and Planar Defects in Titanium.” 2016. link Times cited: 2 USED (low confidence) V. V. Pogorelko and A. Mayer, “Influence of titanium and magnesium nanoinclusions on the strength of aluminum at high-rate tension: Molecular dynamics simulations,” Materials Science and Engineering A-structural Materials Properties Microstructure and Processing. 2016. link Times cited: 27 USED (low confidence) S. Hocker, M. Hummel, P. Binkele, H. Lipp, and S. Schmauder, “Molecular dynamics simulations of tensile tests of Ni-, Cu-, Mg- and Ti-alloyed aluminium nanopolycrystals,” Computational Materials Science. 2016. link Times cited: 12 USED (low confidence) K. Xiong, Y. Zhang, and J. Gu, “Deformation Twinning in Hexagonal Close-Packed Single Crystals under Uniaxial Compression,” Materials Science Forum. 2016. link Times cited: 0 Abstract: In this paper, the uniaxial compression of Mg, Ti, Zr and Co… read moreAbstract: In this paper, the uniaxial compression of Mg, Ti, Zr and Co single crystals along the direction is performed by molecular dynamics (MD) to investigate the elastic-to-plastic transition in these hexagonal close-packed (hcp) metals. Two deformation twinning modes are observed in these simulations, including the twinning in Ti, Zr and Co and the [0001] twinning in Mg. The underlying atomistic mechanisms of these twinning modes are analyzed in detail. read less USED (low confidence) M. Kanani, A. Hartmaier, and R. Janisch, “Stacking fault based analysis of shear mechanisms at interfaces in lamellar TiAl alloys,” Acta Materialia. 2016. link Times cited: 55 USED (low confidence) A. Mayer and P. N. Mayer, “Weak increase of the dynamic tensile strength of aluminum melt at the insertion of refractory inclusions,” Computational Materials Science. 2016. link Times cited: 9 USED (low confidence) H. Hu, X. Wu, R. Wang, W. Li, and Q. Liu, “Phase stability, mechanical properties and electronic structure of TiAl alloying with W, Mo, Sc and Yb: First-principles study,” Journal of Alloys and Compounds. 2016. link Times cited: 48 USED (low confidence) L. E. Kar’kina, I. N. Kar’kin, A. R. Kuznetsov, I. Razumov, P. Korzhavyi, and Y. Gornostyrev, “Solute-grain boundary interaction and segregation formation in Al : First principles calculations and molecular dynamics modeling,” Computational Materials Science. 2016. link Times cited: 33 USED (low confidence) F. Ulomek and V. Mohles, “Separating grain boundary migration mechanisms in molecular dynamics simulations,” Acta Materialia. 2016. link Times cited: 34 USED (low confidence) P. Chowdhury, G. Ren, and H. Sehitoglu, “NiTi superelasticity via atomistic simulations,” Philosophical Magazine Letters. 2015. link Times cited: 41 Abstract: The NiTi shape memory alloys (SMAs) are promising candidates… read moreAbstract: The NiTi shape memory alloys (SMAs) are promising candidates for the next-generation multifunctional materials. These materials are superelastic i.e. they can fully recover their original shape even after fairly large inelastic deformations once the mechanical forces are removed. The superelasticity reportedly stems from atomic scale crystal transformations. However, very few computer simulations have emerged, elucidating the transformation mechanisms at the discrete lattice level, which underlie the extraordinary strain recoverability. Here, we conduct breakthrough molecular dynamics modelling on the superelastic behaviour of the NiTi single crystals, and unravel the atomistic genesis thereof. The deformation recovery is clearly traced to the reversible transformation between austenite and martensite crystals through simulations. We examine the mechanistic origin of the tension–compression asymmetries and the effects of pressure/temperature/strain rate variation isolatedly. Hence, this work essentially brings a new dimension to probing the NiTi performance based on the mesoscale physics under more complicated thermo-mechanical loading scenarios. read less USED (low confidence) S. Xu, Q. Wan, Z. Sha, and Z. Liu, “Molecular dynamics simulations of nano-indentation and wear of the γTi-Al alloy,” Computational Materials Science. 2015. link Times cited: 28 USED (low confidence) Z. Wang et al., “Cyclic deformation leads to defect healing and strengthening of small-volume metal crystals,” Proceedings of the National Academy of Sciences. 2015. link Times cited: 39 Abstract: Significance Producing strong and defect-free materials is a… read moreAbstract: Significance Producing strong and defect-free materials is an important objective in developing many new materials. Thermal treatments aimed at defect elimination often lead to undesirable levels of strength and other properties. Although monotonic loading can reduce or even eliminate dislocations in submicroscale single crystals, such “mechanical healing” causes severe plastic deformation and significant shape changes. Inspired by observing an easier pullout of a partly buried object after shaking it first, we demonstrate that “cyclic healing” of the small-volume single crystals can indeed be achieved through repeated low-amplitude straining. The cyclic healing method points to versatile avenues for tailoring the defect structure and strengthening of nanoscale metal crystals without the need for thermal annealing or severe plastic deformation. When microscopic and macroscopic specimens of metals are subjected to cyclic loading, the creation, interaction, and accumulation of defects lead to damage, cracking, and failure. Here we demonstrate that when aluminum single crystals of submicrometer dimensions are subjected to low-amplitude cyclic deformation at room temperature, the density of preexisting dislocation lines and loops can be dramatically reduced with virtually no change of the overall sample geometry and essentially no permanent plastic strain. This “cyclic healing” of the metal crystal leads to significant strengthening through dramatic reductions in dislocation density, in distinct contrast to conventional cyclic strain hardening mechanisms arising from increases in dislocation density and interactions among defects in microcrystalline and macrocrystalline metals and alloys. Our real-time, in situ transmission electron microscopy observations of tensile tests reveal that pinned dislocation lines undergo shakedown during cyclic straining, with the extent of dislocation unpinning dependent on the amplitude, sequence, and number of strain cycles. Those unpinned mobile dislocations moving close enough to the free surface of the thin specimens as a result of such repeated straining are then further attracted to the surface by image forces that facilitate their egress from the crystal. These results point to a versatile pathway for controlled mechanical annealing and defect engineering in submicrometer-sized metal crystals, thereby obviating the need for thermal annealing or significant plastic deformation that could cause change in shape and/or dimensions of the specimen. read less USED (low confidence) E. Hahn and M. Meyers, “Grain-size dependent mechanical behavior of nanocrystalline metals,” Materials Science and Engineering A-structural Materials Properties Microstructure and Processing. 2015. link Times cited: 162 USED (low confidence) C.-he Fu, L. Sun, and Z. Cheng, “Molecular Dynamics Simulation of Glass Forming Ability of Al30Co10 Amorphous Alloy,” Open Journal of Applied Sciences. 2015. link Times cited: 0 Abstract: By using LAMMPS of the open source software, the micro-struc… read moreAbstract: By using LAMMPS of the open source software, the micro-structures of Al30Co10 alloys were studied. Based on the average atomic volume, pair distribution function and bond-angle distribution functions, Honeycutt-Andersen (HA) bond-type index analysis shows that Al30Co10 alloy system begins to transform into a glass state with the temperature rapidly decreasing to 900 K. The process temperature is decreased from 900 K to 300 K, the radial distribution function g(r) the first peak height with increased, width as decreasing temperature, and the system is an amorphous alloy when second peak appears obvious splitting. The bond angle distribution function showed second peaks when the temperature dropped to 300 K, so that the alloy atoms become orderly. Meanwhile the 1551 bond pairs increase to 35% with decreasing temperature; it implies that the Al30Co10 alloy system can be well transformed into the glass state. read less USED (low confidence) X.-T. Xu, F. Tang, H. Xue, W. Yu, L. Zhu, and Z. Rui, “Molecular dynamics simulations of void shrinkage in γ-TiAl single crystal,” Computational Materials Science. 2015. link Times cited: 22 USED (low confidence) E. S. Wise, M. Liu, and T. Miller, “Sputtering of cubic metal crystals by low-energy xenon-ions,” Computational Materials Science. 2015. link Times cited: 5 USED (low confidence) S. Kalidindi, J. A. Gomberg, Z. Trautt, and C. Becker, “Application of data science tools to quantify and distinguish between structures and models in molecular dynamics datasets,” Nanotechnology. 2015. link Times cited: 39 Abstract: Structure quantification is key to successful mining and ext… read moreAbstract: Structure quantification is key to successful mining and extraction of core materials knowledge from both multiscale simulations as well as multiscale experiments. The main challenge stems from the need to transform the inherently high dimensional representations demanded by the rich hierarchical material structure into useful, high value, low dimensional representations. In this paper, we develop and demonstrate the merits of a data-driven approach for addressing this challenge at the atomic scale. The approach presented here is built on prior successes demonstrated for mesoscale representations of material internal structure, and involves three main steps: (i) digital representation of the material structure, (ii) extraction of a comprehensive set of structure measures using the framework of n-point spatial correlations, and (iii) identification of data-driven low dimensional measures using principal component analyses. These novel protocols, applied on an ensemble of structure datasets output from molecular dynamics (MD) simulations, have successfully classified the datasets based on several model input parameters such as the interatomic potential and the temperature used in the MD simulations. read less USED (low confidence) S. Amokrane, A. Ayadim, and L. Levrel, “Structure of the glass-forming metallic liquids by ab-initio and classical molecular dynamics, a case study: Quenching the Cu60Ti20Zr20 alloy,” Journal of Applied Physics. 2015. link Times cited: 9 Abstract: We consider the question of the amorphization of metallic al… read moreAbstract: We consider the question of the amorphization of metallic alloys by melt quenching, as predicted by molecular dynamics simulations with semi-empirical potentials. The parametrization of the potentials is discussed on the example of the ternary Cu-Ti-Zr transition metals alloy, using the ab-initio simulation as a reference. The pair structure in the amorphous state is computed from a potential of the Stillinger-Weber form. The transferability of the parameters during the quench is investigated using two parametrizations: from solid state data, as usual and from a new parametrization on the liquid structure. When the adjustment is made on the pair structure of the liquid, a satisfactory transferability is found between the pure components and their alloys. The liquid structure predicted in this way agrees well with experiment, in contrast with the one obtained using the adjustment on the solid. The final structure, after quenches down to the amorphous state, determined with the new set of parameters is show... read less USED (low confidence) Z.-C. Xie, T. Gao, X. Guo, and Q. Xie, “Molecular dynamics simulation of nanocrystal formation and deformation behavior of Ti3Al alloy,” Computational Materials Science. 2015. link Times cited: 14 USED (low confidence) S. Kulkova, A. Bakulin, Q. Hu, and R. Yang, “Adsorption and diffusion of oxygen on gamma-TiAl(001) and (100) surfaces,” Computational Materials Science. 2015. link Times cited: 28 USED (low confidence) J. H. Xia, X. Gao, X. Xiao, and Z. Cheng, “Structural properties of coal metallic glasses investigated by molecular dynamics simulations,” Modern Physics Letters B. 2015. link Times cited: 0 Abstract: Based on using molecular dynamics simulations, the structura… read moreAbstract: Based on using molecular dynamics simulations, the structural transitions of Co25Al75 and Co75Al25 were studied during two different quenching processes. The pair-correlation function, the Honeycutt–Andersen (HA) pair analysis technique, Voronoi indices and structural snapshot are adopted in both rapid quenching processes. The results provide direct evidence of the liquid–crystal transition and the liquid Co75Al25 crystallizes into bcc phase at 300 K during the rapid quenching process r1 = 1 K/ps. While during the rapid quenching r2 = 10 K/ps the liquid is frozen into the glass state at 300 K. Meanwhile, the liquid Co25Al75 is frozen into the glass state at 300 K during the two rapid quenching processes. Our results show that the phase formation is strongly dependent on the cooling rates and the compositions. read less USED (low confidence) P. Zhao and L. Fu, “Strain hardening behavior of linear friction welded joints between TC11 and TC17 dissimilar titanium alloys,” Materials Science and Engineering A-structural Materials Properties Microstructure and Processing. 2015. link Times cited: 35 USED (low confidence) Z.-C. Xie, T. Gao, X. Guo, X. Qin, and Q. Xie, “Network connectivity in icosahedral medium-range order of metallic glass: A molecular dynamics simulation,” Journal of Non-crystalline Solids. 2014. link Times cited: 13 USED (low confidence) Z.-C. Xie, T. Gao, X. Guo, and Q. Xie, “Influence of the isothermal process at glass transition temperature on growths of Frank–Kasper polyhedral clusters in TiAl3 alloy,” Journal of Non-crystalline Solids. 2014. link Times cited: 6 USED (low confidence) Z.-C. Xie, T. Gao, X. Guo, X. Qin, and Q. Xie, “Glass formation and icosahedral medium-range order in liquid Ti–Al alloys,” Computational Materials Science. 2014. link Times cited: 15 USED (low confidence) Y.-xia Liu, H. Wang, H. Wu, D. Xu, and R. Yang, “A mean-field interatomic potential for a multi-component β-type titanium alloy,” Computational Materials Science. 2014. link Times cited: 2 USED (low confidence) V. P. Ramunni, “Uranium mobility in face-centered cubic aluminium driven by interstitial migration,” International Journal of Modern Physics B. 2014. link Times cited: 0 Abstract: We characterize the solute mobility behavior driven by inter… read moreAbstract: We characterize the solute mobility behavior driven by interstitial mechanism in FCC diluted alloys using a classical molecular static technique (CMS). In the same line of ideas as the multi-frequency model, we calculate the tracer self- and solute diffusion coefficients. Specifically, we perform our calculations for the Al–U diluted alloy. We verify that in the Al–U system, mixed dumb-bells are observed to be unstable and U mobility is driven by crowdions. From previous results of diffusion in same alloys containing only vacancies, qualitatively we conclude that, experimental data are in perfect agreement with previous calculations of solute U diffusion driven by a vacancy mechanism. Also we give a possible migration path for solute U atoms through interstitial migration, where we have found that U enhances the Al mobility in the alloy. read less USED (low confidence) M. Kanani, A. Hartmaier, and R. Janisch, “Interface properties in lamellar TiAl microstructures from density functional theory,” Intermetallics. 2014. link Times cited: 36 USED (low confidence) P. Zhao, L. Fu, and D. Zhong, “Numerical simulation of transient temperature and axial deformation during linear friction welding between TC11 and TC17 titanium alloys,” Computational Materials Science. 2014. link Times cited: 38 USED (low confidence) Z.-C. Xie, T. Gao, X. Guo, X. Qin, and Q. Xie, “Growth of icosahedral medium-range order in liquid TiAl alloy during rapid solidification,” Journal of Non-crystalline Solids. 2014. link Times cited: 14 USED (low confidence) S. Kiselev and E. V. Zhirov, “Molecular-dynamics simulation of the synthesis of intermetallic Ti–Al,” Intermetallics. 2014. link Times cited: 24 USED (low confidence) Z.-C. Xie, T. Gao, X. Guo, X. Qin, and Q. Xie, “Evolution of icosahedral clusters during the rapid solidification of liquid TiAl alloy,” Physica B-condensed Matter. 2014. link Times cited: 12 USED (low confidence) T. Liu, Z. Cheng, J. H. Xia, X. Xiao, and H. Huang, “Simulation of Structural Transition of Ni Nano-Material under Different Pressures,” Applied Mechanics and Materials. 2014. link Times cited: 0 Abstract: In this paper, the structural transitions of the rapidly coo… read moreAbstract: In this paper, the structural transitions of the rapidly cooled Ni nanomaterial under different pressures were studied by using molecular dynamics simulation. The work gives the structural properties, including the potential energy, pair-correlation function and Honeycutt-Andersen (HA) and Voronoi indices. This pair-correlation function of liquid Ni agrees well with the experimental results. The local structures are characterized by Honeycutt-Andersen (HA) indices and Voronoi tessellation. Our results indicate that with the increasing pressure the Ni nanomaterial transformed from the disordered structure to the ordered structure. The icosahedral and defect icosahedral decrease, the hcp-like structure increased at 300 K. These phenomena were shown that the crystalline state is hcp-like local structure. read less USED (low confidence) J. W. Wang and H. Gong, “Adsorption and diffusion of hydrogen on Ti, Al, and TiAl surfaces,” International Journal of Hydrogen Energy. 2014. link Times cited: 34 USED (low confidence) H. Men and Z. Fan, “Atomic ordering in liquid aluminium induced by substrates with misfits,” Computational Materials Science. 2014. link Times cited: 38 USED (low confidence) M. Gerboth, W. Setyawan, and C. Henager, “Displacement Threshold Energy and Recovery in an Al-Ti Nanolayered System with Intrinsic Point Defect Partitioning,” Computational Materials Science. 2014. link Times cited: 3 USED (low confidence) D. Xu, H. Wang, R. Yang, and A. Sachdev, “MD simulation of asymmetric nucleation and motion of 〈011] superdislocations in TiAl,” Chinese Science Bulletin. 2014. link Times cited: 10 USED (low confidence) F. Tang et al., “Molecular dynamics simulations of void growth in γ-TiAl single crystal,” Computational Materials Science. 2014. link Times cited: 34 USED (low confidence) C. Song, T. Lin, P. He, Z. Jiao, J. Tao, and Y. Ji, “Molecular dynamics simulation of linear friction welding between dissimilar Ti-based alloys,” Computational Materials Science. 2014. link Times cited: 35 USED (low confidence) R. Voskoboinikov, “An insight into the mechanism of SFT formation near 1/2 ‹110› edge dislocations in aluminum exposed to irradiation.” 2014. link Times cited: 0 USED (low confidence) N. Huynh, C. Lu, G. Michal, and A. K. Tieu, “A Misorientation Dependent Criterion of Crack Opening in FCC Single Crystal,” Materials Science Forum. 2013. link Times cited: 0 Abstract: This paper proposes a criterion for crack opening in FCC sin… read moreAbstract: This paper proposes a criterion for crack opening in FCC single crystals based on analyses of lattice orientation and interface energy of two adjacent crystals in a crystal plasticity finite element model (CPFEM). It also demonstrates the implementation of the criterion in Abaqus/Standard to simulate crack initiation and propagation in single-edged notch single crystal aluminium samples. Elements in the FEM mesh that have crystalline structures satisfying the crack opening criterion are removed from the mesh at the end of every loading step and FEM analyses are restarted on the new mesh in the next loading step. Removed elements effectively act as voids in the material due to crack nucleation. Similarly, the coalescence of newly removed elements at the end of a loading step with the existent ones simulates crack growth in the material. Two advantages of this approach are noted. Firstly, crack nucleation and its subsequent growth in the material is simulated solely based on lattice evolution history in the material without any presumptions of crack paths or regions where cracks are likely to occur. Secondly, as the criterion for crack nucleation is evaluated based on, and thus changes with, the lattice evolution during loading, a predefined energy criterion for crack opening, which could be erroneous, is avoided. Preliminary results of void nucleation and void growth around the notch tip in Cube and Brass oriented samples using CPFEM modelling appear to agree with molecular dynamics simulations of void growth in FCC single crystals. read less USED (low confidence) E. Levchenko, A. Evteev, T. Lorscheider, I. Belova, and G. Murch, “Molecular dynamics simulation of alloying in an Al-coated Ti nanoparticle,” Computational Materials Science. 2013. link Times cited: 15 USED (low confidence) M. A. Bhatia and K. Solanki, “Energetics of vacancy segregation to symmetric tilt grain boundaries in hexagonal closed pack materials,” Journal of Applied Physics. 2013. link Times cited: 34 Abstract: Molecular static simulations of 190 symmetric tilt grain bou… read moreAbstract: Molecular static simulations of 190 symmetric tilt grain boundaries in hexagonal closed pack metals were used to understand the energetics of vacancy segregation, which is important for designing stable interfaces in harsh environments. Simulation results show that the local arrangements of grain boundaries and the resulting structural units have a significant influence on the magnitude of vacancy binding energies, and the site-to-site variation within each boundary is substantial. Comparing the vacancy binding energies for each site in different c/a ratio materials shows that the binding energy increases significantly with an increase in c/a ratio. For example, in the [12¯10] tilt axis, Ti and Zr with c/a = 1.5811 have a lower vacancy binding energy than the Mg with c/a = 1.6299. Furthermore, when the grain boundary energies of all 190 boundaries in all three elements are plotted against the vacancy binding energies of the same boundaries, a highly negative correlation (r = −0.7144) is revealed that has ... read less USED (low confidence) D. Zhang, X. M. Gao, X. Xiao, Z. Cheng, and J. H. Xia, “Molecular Dynamics Simulations of Atomic Structure in Cu46Zr46Al8 Metallic Liquid and Glass,” Advanced Materials Research. 2013. link Times cited: 0 Abstract: The microscopic structure Cu46Zr46Al8 alloys were investigat… read moreAbstract: The microscopic structure Cu46Zr46Al8 alloys were investigated by means of molecular dynamics simulations. This work gives the structure properties including partial pair-correlation function, pair analysis technique and Voronoi indices, and the temperature dependence. The simulated pair-correlation function is consistent well with the experimental one. We found that the the fractions of icosahedra and the distorted icosahedra increase with the decreasing temperature and become into the dominant clusters in the bulk metallic glass. At the meanwhile, we found that the icosahedra and the distorted icosahedra around Cu, Zr and Al are different. The Cu-center and Al-center icosahedra and the distorted icosahedra increase with the decreasing temperature, but The Zr-center icosahedra and the distorted icosahedra decrease with the decreasing temperature. read less USED (low confidence) J. H. Xia, X. Gao, Z. Cheng, and X. Xiao, “Simulations of Structural Transition of Ti75Al25 under High Pressure,” Applied Mechanics and Materials. 2013. link Times cited: 0 Abstract: The structural transitions of the rapidly cooled Ti75Al25 un… read moreAbstract: The structural transitions of the rapidly cooled Ti75Al25 under high pressures were studied by using molecular dynamics simulations. This work gives the structural properties, including the potential energy, pair-correlation function, Honeycutt-Andersen (HA) and Voronoi indices, and temperature dependence. Our results indicated that the liquid Ti75Al25 was frozen into glass state at the temperature about 300 K under different pressures during the same quenching processes. With increasing of pressure, the glass transformation temperature (Tg) become high. The icosahedral and defect icosahedral clusters increase as the temperature decreases under different pressures. But the icosahedral cluster increases with the increasing pressure and defect icosahedral clusters keeps invariability at 300 K. read less USED (low confidence) A. Singh, R. Sankarasubramanian, and T. Nandy, “Mobilities and dislocation energies of planar faults in an ordered A3B (D019) structure,” Bulletin of Materials Science. 2013. link Times cited: 1 USED (low confidence) S. Jiang, Y. Shen, Y. Zheng, and Z. Chen, “Formation of quasi-icosahedral structures with multi-conjoint fivefold deformation twins in fivefold twinned metallic nanowires,” Applied Physics Letters. 2013. link Times cited: 15 Abstract: We show by molecular dynamics simulations that symmetrical q… read moreAbstract: We show by molecular dynamics simulations that symmetrical quasi-icosahedral structures can be formed in fivefold twinned metallic nanowires (Cu, Au, and Ag) under dynamic tensile loading. The quasi-icosahedral structure, different from the icosahedral nanoclusters found in the past, consists of a twisted original fivefold twinned axis and ten secondary fivefold deformation twins, with five preexisting prismatic and fifteen tetrahedral subunits joined adjacently. Formation of these structures is observed in the necking region during the plastic deformation with successive twinning processes and is found to be independent on the cross-sectional shape as well as the tensile strain rate of the nanowires. read less USED (low confidence) R. Voskoboinikov, “Molecular dynamics simulations of radiation damage in D019 Ti3Al intermetallic compound,” Nuclear Instruments & Methods in Physics Research Section B-beam Interactions With Materials and Atoms. 2013. link Times cited: 9 USED (low confidence) J. Michalka, P. McIntyre, and J. Gezelter, “Molecular Dynamics Simulations of the Surface Reconstructions of Pt(557) and Au(557) under Exposure to CO,” Journal of Physical Chemistry C. 2013. link Times cited: 5 Abstract: The mechanism and dynamics of surface reconstructions of Pt(… read moreAbstract: The mechanism and dynamics of surface reconstructions of Pt(557) and Au(557) exposed to various coverages of carbon monoxide (CO) were investigated using molecular dynamics simulations. Metal–CO interactions were parametrized from experimental data and plane-wave density functional theory (DFT) calculations. The large difference in binding strengths of the Pt–CO and Au–CO interactions was found to play a significant role in step-edge stability and adatom diffusion constants. Various mechanisms for CO-mediated step wandering and step doubling were investigated on the Pt(557) surface. We find that the energetics of CO adsorbed to the surface can explain the step-doubling reconstruction observed on Pt(557) and the lack of such a reconstruction on the Au(557) surface. However, more complicated reconstructions into triangular clusters that have been seen in recent experiments were not observed in these simulations. read less USED (low confidence) M. A. Karolewski, R. Cavell, R. Gordon, C. Glover, M. Cheah, and M. Ridgway, “Predicting XAFS scattering path cumulants and XAFS spectra for metals (Cu, Ni, Fe, Ti, Au) using molecular dynamics simulations.,” Journal of synchrotron radiation. 2013. link Times cited: 5 Abstract: The ability of molecular dynamics (MD) simulations to suppor… read moreAbstract: The ability of molecular dynamics (MD) simulations to support the analysis of X-ray absorption fine-structure (XAFS) data for metals is evaluated. The low-order cumulants (ΔR, σ(2), C3) for XAFS scattering paths are calculated for the metals Cu, Ni, Fe, Ti and Au at 300 K using 28 interatomic potentials of the embedded-atom method type. The MD cumulant predictions were evaluated within a cumulant expansion XAFS fitting model, using global (path-independent) scaling factors. Direct simulations of the corresponding XAFS spectra, χ(R), are also performed using MD configurational data in combination with the FEFF ab initio code. The cumulant scaling parameters compensate for differences between the real and effective scattering path distributions, and for any errors that might exist in the MD predictions and in the experimental data. The fitted value of ΔR is susceptible to experimental errors and inadvertent lattice thermal expansion in the simulation crystallites. The unadjusted predictions of σ(2) vary in accuracy, but do not show a consistent bias for any metal except Au, for which all potentials overestimate σ(2). The unadjusted C3 predictions produced by different potentials display only order-of-magnitude consistency. The accuracy of direct simulations of χ(R) for a given metal varies among the different potentials. For each of the metals Cu, Ni, Fe and Ti, one or more of the tested potentials was found to provide a reasonable simulation of χ(R). However, none of the potentials tested for Au was sufficiently accurate for this purpose. read less USED (low confidence) R. Voskoboinikov, “MD simulations of collision cascades in the vicinity of a screw dislocation in aluminium,” Nuclear Instruments & Methods in Physics Research Section B-beam Interactions With Materials and Atoms. 2013. link Times cited: 31 USED (low confidence) R. Voskoboinikov, “MD study of primary damage in L10 TiAl structural intermetallics,” Nuclear Instruments & Methods in Physics Research Section B-beam Interactions With Materials and Atoms. 2013. link Times cited: 5 USED (low confidence) R. Voskoboinikov, “Interaction of collision cascades with an isolated edge dislocation in aluminium,” Nuclear Instruments & Methods in Physics Research Section B-beam Interactions With Materials and Atoms. 2013. link Times cited: 29 USED (low confidence) Y. Zhu, Z. Li, and M. Huang, “Coupled effect of sample size and grain size in polycrystalline Al nanowires,” Scripta Materialia. 2013. link Times cited: 33 USED (low confidence) S. Rao, A. Venkateswaran, and M. Letherwood, “Molecular statics and molecular dynamics simulations of the critical stress for motion of a /3 〈112¯0〉 screw dislocations in α-Ti at low temperatures using a modified embedded atom method potential,” Acta Materialia. 2013. link Times cited: 18 USED (low confidence) Q. Hu and R. Yang, “Basal-plane stacking fault energy of hexagonal close-packed metals based on the Ising model,” Acta Materialia. 2013. link Times cited: 42 USED (low confidence) H. Wang, R. Reed, J. Gebelin, and N. Warnken, “On the modelling of the point defects in the ordered B2 phase of the Ti–Al system: Combining CALPHAD with first-principles calculations,” Calphad-computer Coupling of Phase Diagrams and Thermochemistry. 2012. link Times cited: 20 USED (low confidence) L. Xiong, Q. Deng, G. Tucker, D. McDowell, and Y. Chen, “Coarse-Grained Atomistic Simulations of Dislocations in Al Ni and Cu Crystals.,” International Journal of Plasticity. 2012. link Times cited: 66 USED (low confidence) C. DaSilva and J. Rino, “Atomistic simulation of the deformation mechanism during nanoindentation of gamma titanium aluminide,” Computational Materials Science. 2012. link Times cited: 16 USED (low confidence) M. I. Pascuet, V. P. Ramunni, and J. R. Fernández, “Point defect properties in the vicinity of an Al/U interface,” Physica B-condensed Matter. 2012. link Times cited: 3 USED (low confidence) J. H. Xia, Z. Cheng, D. Shi, and X. Xiao, “A molecular dynamics study of structural transition of Ti during the rapid quenching process,” Physica B-condensed Matter. 2012. link Times cited: 4 USED (low confidence) M. Horstemeyer, “Case Study: Conducting a Structural Scale Metal Forming Finite Element Analysis Starting from Electronics Structures Calculations Using ICME Tools.” 2012. link Times cited: 0 USED (low confidence) M. I. Pascuet, G. Bonny, and J. R. Fernández, “Many-body interatomic U and Al–U potentials,” Journal of Nuclear Materials. 2012. link Times cited: 28 USED (low confidence) X.-J. Yuan, N. Chen, and J. Shen, “Construction of embedded-atom-method interatomic potentials for alkaline metals (Li, Na, and K) by lattice inversion,” Chinese Physics B. 2012. link Times cited: 1 Abstract: The lattice-inversion embedded-atom-method interatomic poten… read moreAbstract: The lattice-inversion embedded-atom-method interatomic potential developed previously by us is extended to alkaline metals including Li, Na, and K. It is found that considering interatomic interactions between neighboring atoms of an appropriate distance is a matter of great significance in constructing accurate embedded-atom-method interatomic potentials, especially for the prediction of surface energy. The lattice-inversion embedded-atom-method interatomic potentials for Li, Na, and K are successfully constructed by taking the fourth-neighbor atoms into consideration. These angular-independent potentials markedly promote the accuracy of predicted surface energies, which agree well with experimental results. In addition, the predicted structural stability, elastic constants, formation and migration energies of vacancy, and activation energy of vacancy diffusion are in good agreement with available experimental data and first-principles calculations, and the equilibrium condition is satisfied. read less USED (low confidence) E. Levchenko, A. Evteev, G. Löwisch, I. Belova, and G. Murch, “Molecular dynamics simulation of alloying in a Ti-coated Al nanoparticle,” Intermetallics. 2012. link Times cited: 24 USED (low confidence) K. Zhou, H. Wang, and B. Wei, “Determining thermophysical properties of undercooled liquid Ti–Al alloy by electromagnetic levitation,” Chemical Physics Letters. 2012. link Times cited: 23 USED (low confidence) X.-J. Yuan, N. Chen, and J. Shen, “Lattice-Inversion Embedded-Atom-Method Interatomic Potentials for Group-VA Transition Metals,” Chinese Physics Letters. 2011. link Times cited: 1 Abstract: The lattice-inversion embedded-atom-method (LI-EAM) interato… read moreAbstract: The lattice-inversion embedded-atom-method (LI-EAM) interatomic potential we developed previously [J. Phys.: Condens. Matter 22 (2010) 375503] is extended to group-VA transition metals (V, Nb and Ta). It is found that considering interatomic interactions up to appropriate-distance-neighbor atoms is crucial to constructing accurate EAM potentials, especially for the prediction of surface energy. The LI-EAM interatomic potentials for group-VA transition metals are successfully built by considering interatomic interactions up to the fifth neighbor atoms. These angular-independent potentials drastically promote the accuracy of the predicted surface energies, which match the experimental results well. read less USED (low confidence) E. Tadmor and R. E. Miller, “Modeling Materials: Continuum, Atomistic and Multiscale Techniques.” 2011. link Times cited: 395 Abstract: 1. Introduction Part I. Continuum Mechanics and Thermodynami… read moreAbstract: 1. Introduction Part I. Continuum Mechanics and Thermodynamics: 2. Essential continuum mechanics and thermodynamics Part II. Atomistics: 3. Lattices and crystal structures 4. Quantum mechanics of materials 5. Empirical atomistic models of materials 6. Molecular statics Part III. Atomistic Foundations of Continuum Concepts: 7. Classical equilibrium statistical mechanics 8. Microscopic expressions for continuum fields 9. Molecular dynamics Part IV. Multiscale Methods: 10. What is multiscale modeling? 11. Atomistic constitutive relations for multilattice crystals 12. Atomistic/continuum coupling: static methods 13. Atomistic/continuum coupling: finite temperature and dynamics Appendix References Index. read less USED (low confidence) J. Xia, C. S. Liu, Z. Cheng, and D. Shi, “Molecular dynamics simulations on local structure and diffusion in liquid TixAl1−x alloys,” Physica B-condensed Matter. 2011. link Times cited: 5 USED (low confidence) Y. Wei, H.-B. Zhou, Y. Zhang, G. Lu, and H. Xu, “Effects of O in a binary-phase TiAl–Ti3Al alloy: from site occupancy to interfacial energetics,” Journal of Physics: Condensed Matter. 2011. link Times cited: 28 Abstract: We have investigated site occupancy and interfacial energeti… read moreAbstract: We have investigated site occupancy and interfacial energetics of a TiAl–Ti3Al binary-phase system with O using a first-principles method. Oxygen is shown to energetically occupy the Ti-rich octahedral interstitial site, because O prefers to bond with Ti rather than Al. The occupancy tendency of O in TiAl alloy from high to low is α2-Ti3Al to the γ-α2 interface and γ-TiAl. We demonstrate that O can largely affect the mechanical properties of the TiAl–Ti3Al system. Oxygen at the TiAl–Ti3Al interface reduces both the cleavage energy and the interface energy, and thus weakens the interface strength but strongly stabilizes the TiAl/Ti3Al interface with the O2 molecule as a reference. Consequently, the mechanical property variation of TiAl alloy due to the presence of O not only depends on the number of TiAl/Ti3Al interfaces but also is related to the O concentration in the alloy. read less USED (low confidence) Y. Liu, J. Bao, L. Zhang, S. Wang, and H. Ye, “Moleculer Dynamics Study of the Thermodynamic Shear Deformation in TiAl/Ti3Al System,” Materials Science Forum. 2011. link Times cited: 4 Abstract: TiAl alloys have great potential because of its low density … read moreAbstract: TiAl alloys have great potential because of its low density and the outstanding performance at high temperature. However, the brittleness influences its industrialization process. It is known that the macroscopic nature is greatly influenced by its microscopic structure, and the fault development plays a vital role during the material working process. The paper performed the molecular dynamics (MD) study of the thermodynamic shear deformation in TiAl/Ti3Al system to promote the understanding in this aspect. Above all, we adopt a special shear deformation model based on the experimental consideration, and conduct the optimal calculation of the related parameters. Then, a series of thermodynamic deformation simulation were carried out using the previous optimized model. The analysis of the potential variation and the structural snapshots showed that the shear deformation is related with the “stick-slip” behavior. The Ti3Al (TiAl) shows obvious (little) covariant deformation stage before the initiation of the fault transition. For Ti3Al region near the interface, the final structure is the continued FCC stacking. For TiAl, twin and SISF are observed and the block of twin is the main remnant. The atomic diffusion is locally observed in Ti3Al phase. The interface transits the energy and counterpoises the deformation between the hetero-phases. read less USED (low confidence) P. Tang, B. Y. Tang, and X. Su, “First-principles studies of typical long-period superstructures Al5Ti3, h-Al2Ti and r-Al2Ti in Al-rich TiAl alloys,” Computational Materials Science. 2011. link Times cited: 29 USED (low confidence) O. Peyrusse, “Real-space finite-difference calculations of XANES spectra along the aluminum Hugoniot from molecular dynamics simulations,” High Energy Density Physics. 2010. link Times cited: 9 USED (low confidence) O. Semenova, “A statistical-thermodynamic modeling of behavior and properties in thin-film intermetallics with D019-structure,” Materials Letters. 2010. link Times cited: 2 USED (low confidence) G. Kimminau, P. Erhart, E. Bringa, B. Remington, and J. Wark, “Phonon instabilities in uniaxially compressed fcc metals as seen in molecular dynamics simulations,” Physical Review B. 2010. link Times cited: 19 Abstract: We show that the generation of stacking faults in perfect fa… read moreAbstract: We show that the generation of stacking faults in perfect face-centered-cubic (fcc) crystals, uniaxially compressed along [001], is due to transverse-acoustic phonon instabilities. The position in reciprocal space where the instability first manifests itself is not a point of high symmetry in the Brillouin zone. This model provides a useful explanation for the magnitude of the elastic limit, in addition to the affects of box size, temperature, and compression on the time scale for the generation of stacking faults. We observe this phenomenon in both simulations that use the Lennard-Jones potential and embedded atom potentials. Not only does this work provide fundamental insight into the microscopic response of the material but it also describes certain behavior seen in previous molecular dynamics simulations of single-crystal fcc metals shock compressed along the principal axis. read less USED (low confidence) H. Yildirim, A. Kara, T. Rahman, R. Heid, and K. Bohnen, “Surface vibrational thermodynamics from ab initio calculations for fcc(1 0 0),” Surface Science. 2010. link Times cited: 5 USED (low confidence) K. Sato, S. Takizawa, S. Miura, and T. Mohri, “A Kinetic Monte Carlo Simulation of Ordering Process in Ti-Al System,” Journal of the Physical Society of Japan. 2009. link Times cited: 0 Abstract: We perform kinetic Monte Carlo simulations of atomic diffusi… read moreAbstract: We perform kinetic Monte Carlo simulations of atomic diffusion in the Ti–Al system using activation energies calculated by embedded atom method (EAM). The activation energies strongly depend on the atomic species occupying the four atomic sites which locate nearest to the saddle point in the fcc lattice. It is found, however, that the configuration of atoms on the other sites surrounding the jumping atom plays an essential role in the atomic ordering process: we fail to reproduce the formation of ordered nuclei in using the activation energies which depend only on the configuration of the nearest four atoms, and the system remains in disordered states even at very low temperatures. By introducing a correction term to the activation energies which takes into account the contribution of nearest neighbor atoms of the migrating atom, we can simulate growth of ordered embrios. read less USED (low confidence) H. Wang, D. Xu, R.-fu Yang, and P. Veyssiére, “The transformation of narrow dislocation dipoles in selected fcc metals and in γ-TiAl,” Acta Materialia. 2009. link Times cited: 34 USED (low confidence) H. Gong, “Electronic structure and related properties of Pd/TiAl membranes,” Intermetallics. 2009. link Times cited: 35 USED (low confidence) D. Xu, H. Wang, R. Yang, and P. Veyssiére, “Point defect formation by dislocation reactions in TiAl.” 2009. link Times cited: 12 Abstract: Point defect formation in γ-TiAl deformed in single slip is … read moreAbstract: Point defect formation in γ-TiAl deformed in single slip is investigated by MD simulations. Dislocations gliding on nearby planes react to form vacancies, interstitials and clusters of these, including planar arrays of crowdions and dissociated prismatic loops. The motion of these defects and their interaction with mobile dislocations are analysed. These point defects can interact with others or with dislocations forming jogs hindering dislocation motion. read less USED (low confidence) N. Tarrat, M. Benoit, and J. Morillo, “Core structure of screw dislocations in hcp Ti: an ab initio DFT study,” International Journal of Materials Research. 2009. link Times cited: 21 Abstract: The core structure of screw dislocations in -Ti was studied … read moreAbstract: The core structure of screw dislocations in -Ti was studied in the cluster approach with ab initio DFT-GGA, and in both the cluster and quadrupole approaches with a recently highly optimized EAM central force potential. With the EAM potential we have shown that finite-size effects, in the cluster approach, are negligible down to the size studied in the ab initio DFT calculations that have shown unambiguously a preferential prismatic core spreading for the dislocation. Our results are in agreement with previously published approximated calculations using empirical or semi-empirical interaction models: only approximated interaction models, taking explicitly into account the covalent directional bonding of the d electrons, can properly account for the preferential prismatic core spreading against the basal one; and empirical interaction models without angular force components are inadequate. Interestingly, at first sight, the relaxed core structures (basal or prismatic) obtained with empirical or semi-empirical interaction models are almost identical to the ones obtained with the ab initio DFT calculations. read less USED (low confidence) C. Jiang, “First-principles study of site occupancy of dilute 3d, 4d and 5d transition metal solutes in L10 TiAl,” Acta Materialia. 2008. link Times cited: 44 USED (low confidence) D. Xu, H. Wang, R. Yang, and P. Veyssiére, “Molecular dynamics investigation of deformation twinning in γ-TiAl sheared along the pseudo-twinning direction,” Acta Materialia. 2008. link Times cited: 41 USED (low confidence) M. Pozzo, D. Alfé, A. Amieiro, S. French, and A. Pratt, “Hydrogen dissociation and diffusion on Ni- and Ti-doped Mg(0001) surfaces.,” The Journal of chemical physics. 2008. link Times cited: 68 Abstract: It is well-known, both theoretically and experimentally, tha… read moreAbstract: It is well-known, both theoretically and experimentally, that alloying MgH(2) with transition elements can significantly improve the thermodynamic and kinetic properties for H(2) desorption, as well as the H(2) intake by Mg bulk. Here, we present a density functional theory investigation of hydrogen dissociation and surface diffusion over a Ni-doped surface and compare the findings to previously investigated Ti-doped Mg(0001) and pure Mg(0001) surfaces. Our results show that the energy barrier for hydrogen dissociation on the pure Mg(0001) surface is high, while it is small/null when NiTi are added to the surface as dopants. We find that the binding energy of the two H atoms near the dissociation site is high on Ti, effectively impeding diffusion away from the Ti site. By contrast, we find that on Ni, the energy barrier for diffusion is much reduced. Therefore, although both Ti and Ni promote H(2) dissociation, only Ni appears to be a good catalyst for Mg hydrogenation, allowing diffusion away from the catalytic sites. Experimental results corroborate these theoretical findings, i.e., faster hydrogenation of the Ni-doped Mg sample as opposed to the reference Mg- or Ti-doped Mg. read less USED (low confidence) K. Moriguchi and M. Igarashi, “Correlation between lattice-strain energetics and melting properties: Molecular dynamics and lattice dynamics using EAM models of Al,” Physical Review B. 2006. link Times cited: 14 USED (low confidence) J. Schuster and M. Palm, “Reassessment of the binary Aluminum-Titanium phase diagram,” Journal of Phase Equilibria and Diffusion. 2006. link Times cited: 349 USED (low confidence) Y. Mishin, “Atomistic Computer Modeling of Intermetallic Alloys,” Materials Science Forum. 2005. link Times cited: 3 Abstract: The paper gives a brief overview of our recent work on atomi… read moreAbstract: The paper gives a brief overview of our recent work on atomistic computer modeling of ordered intermetallic compounds of the Ni-Al and Ti-Al systems. Atomic interactions in these systems are modeled by semi-empirical potentials fit to experimental and first-principles data. The methodology includes a large variety of techniques ranging from harmonic lattice dynamics to molecular dynamics and Monte Carlo simulations. The properties studied include lattice characteristics (elastic constants, phonons, thermal expansion), point-defect properties, atomic diffusion, generalized stacking faults, dislocations, surfaces, grain boundaries, interphase boundaries, and phase diagrams. We especially emphasize the recent progress in the understanding of diffusion mechanisms in NiAl and TiAl, calculation of stacking fault energies in Ni3Al in relation to dislocation behavior, and calculations of / 0 interface boundaries in Ni-Al alloys. read less USED (low confidence) Y. Mishin, I. Belova, and G. Murch, “Atomistic Modeling of Diffusion in the TiAl Compound,” Defect and Diffusion Forum. 2005. link Times cited: 11 Abstract: We combine atomistic modeling methods with kinetic Monte sim… read moreAbstract: We combine atomistic modeling methods with kinetic Monte simulations to study selfdiffusion in the intermetallic compound L -TiAl. Atomic interactions in TiAl are modeled with a recently developed embedded-atom potential. The vacancy concentration in TiAl is obtained from a lattice gas model of non-interacting point defects. Molecular dynamics simulations are applied to determine vacancy migration mechanisms in the compound. A set of representative vacancy jumps is identified and their rate constants are computed using the harmonic transition state theory with the reaction path established by the nudged elastic band method. The rate constants are used as input to kinetic Monte Carlo simulations performed at several temperatures and alloy compositions. KMC simulations give us self-diffusion coefficients of Ti and Al, correlation factors and other diffusion characteristics. The results are in reasonable agreement with experimental data. We conclude that our methodology provides a viable approach to diffusion calculations in ordered intermetallic compounds. Introduction Titanium aluminide TiAl is a technologically important structural material due to its hightemperature applications in the aerospace industry. It crystallizes in the L structure containing alternating Ti and Al layers parallel a plane. Atomic diffusion has a significant impact on many properties of TiAl, including kinetics of phase transformations, creep resistance, oxidation resistance, etc. Ti self-diffusion, interdiffusion and diffusion of various impurities in TiAl have been studied over the recent years (see [1] for a review). It has been established by Ti radiotracer measurements that diffusion parallel to the -axis (i.e. normal to layers) is about a factor of ten slower than along layers [2, 3]. No reliable experimental data are available for Al self-diffusion due to the lack of a suitable radiotracer. Al diffusion in TiAl has only been estimated by inverting the Darken-Manning equation using interdiffusion and Ti self-diffusion data combined with experimental thermodynamic factors [1]. On the theoretical side, barriers of typical vacancy jumps in TiAl have been calculated with an embedded-atom method (EAM) potential and a preliminary evaluation of several plausible diffusion mechanisms has been made [1, 4]. Those barriers were also employed to explain the diffusion anisotropy in TiAl through vacancy jump correlations [2, 5]. Predictive capabilities of the previous calculations were limited for a number of reasons. The EAM potential used in [1, 4] was not reliable enough to produce more than rough estimates. Point-defect formation entropies were neglected and the frequency factors of all vacancy jumps were assumed to be identical. The diffusion mechanisms examined in [1, 4] were selected from geometric considerations or by analogy with other compounds. Perhaps more importantly, the relative contribution of different diffusion mechanisms was assessed from their estimated activation energies without calculating the absolute values of the relevant diffusion coefficients. The latter would require the incorporation of jump correlation effects, which Defect and Diffusion Forum Online: 2005-04-30 ISSN: 1662-9507, Vols. 237-240, pp 271-276 doi:10.4028/www.scientific.net/DDF.237-240.271 © 2005 Trans Tech Publications Ltd, Switzerland All rights reserved. No part of contents of this paper may be reproduced or transmitted in any form or by any means without the written permission of Trans Tech Publications Ltd, www.scientific.net. (Semanticscholar.org-13/03/20,21:57:18) was not done properly in the previous work. In this paper we revisit diffusion in TiAl with a more advanced approach based on more accurate atomistic simulations combined with the kinetic Monte Carlo (KMC) method. This approach allows us to analyze diffusion in TiAl in terms of absolute values of diffusion coefficients and compare them with experimental data. Methodology Point-defect concentrations. Atomic interactions in TiAl are described with an EAM potential fit to a large database of experimental and first-principles data [6]. This is believed to be the most accurate EAM potential currently available for this compound. In calculating the equilibrium vacancy concentration, we take into account that vacancies can occupy either of the two sublattices (V and V ) and are in dynamic equilibrium with antisites on both sublattices (Ti and Al ). We thus use a lattice-gas model in which the point defects are teated as a four-component gas in equilibrium with respect to all possible defect reactions [1]. The equilibrium defect concentrations are determined by numerically solving a set of three independent mass-action law relations augmented with a material conservation equation. The input data for the calculation are the free energy of the perfect lattice and free energies of the individual point defects V V Ti and Al . The energies and are obtained by molecular statics while the entropies and are calculated within the classical harmonic approximation [6]. This procedure allows us to find the total vacancy concentration as a function temperature and the alloy composition. The compositional dependence of turns out to be relative weak. The temperature dependence of does not follow the Arrhenius Law exactly but can be approximated by the Arrhenius relation in a chosen temperature interval to give the “effective” vacancy formation energy. It should be mentioned that is orders of magnitude smaller than both antisite concentrations. Vacancies prefer the Ti sublattice except in Al-rich compositions with at.% Ti. Diffusion mechanisms. To study diffusion mechanisms, molecular dynamics simulations (MD) are run on a perfect-lattice block containing a single vacancy. The computer code automatically saves a snapshot whenever large atomic displacements point to a possible vacancy jump. By examining multiple snapshots, which we combine into a movie, we are able to determine typical diffusion mechanisms of the vacancy. The MD simulations have been performed at temperatures , "! and K. The diffusion mechanisms observed do not depend on temperature and can be summarized as follows. A Ti vacancy prefers to move along Ti layers by exchanging with either Ti atoms or Al antisites. It occasionally jumps to an adjacent Al layer (thus leaving an Al antisite behind) but such jumps tend to be quickly reversed. In cases where they are not reversed, the vacancy typically makes one jump on the Al layer and returns to its latest position in the Ti layer, thus eliminating the Al antisite. This correlated jump sequence, identified in [1] as the three-jump cycle mechanism, results in an exchange of two Al atoms on the Al sublattice due to a Ti vacancy. An Al vacancy is observed to move along Al layers with occasional jumps to a neighboring Ti layer. Three-jump cycles of Al vacancies, although geometrically possible [1], have not been observed in the MD simulations. No six-jump cycles of either Ti or Al vacancies have been found. In contrast to B2-NiAl where vacancies can make collective jumps involving two atoms [7], only single-atom exchanges with a vacancy are observed in TiAl. As the vacancy moves, it first produces antisites, some of them are later eliminated, and the crystal approaches point-defect equilibrium. The presence of scattered antisites at later stages of the simulation does not give rise to any new diffusion mechanisms. Overall, the picture of diffusion can be described as correlated vacancy motion both along and between layers, with interlayer jumps resulting in the production or elimination of antisites. Jump correlations are significant but not strong enough for a domination of cycles. KMC catalog. To prepare catalog-based KMC simulations, we have identified a set of the most typical vacancy jumps. They include both intraand inter-sublattice jumps of Ti and Al vacancies, in each case for exchanges with either a regular atom or an antisite. Furthermore, we have taken into 272 Diffusion in Materials DIMAT2004 read less USED (low confidence) L. Zhou, L. Hsiung, and H.-C. Huang, “Nucleation and Propagation of Deformation Twin in Polysynthetically Twinned TiAl,” Cmes-computer Modeling in Engineering & Sciences. 2004. link Times cited: 3 Abstract: Using molecular dynamics simulations, we have studied the de… read moreAbstract: Using molecular dynamics simulations, we have studied the deformation of polysynthetically twinned (PST) TiAl at room temperature with a bicrystal model. The simulation cell was pre-strained and thermodynamically relaxed to a criterion that all stress components of the simulation cell have gone to zeros; in this way no dislocations were pre-existed in {gamma}-{alpha}{sub 2} interfaces. A uniaxial compression was then applied along one 1/6<112] direction in the surface. The results show that under the compression, the interfacial dislocation pairs were prolifically generated due to the structural transformation of {alpha}{sub 2}-lamella. The gliding and agglomerating of these dislocations would finally cause the nucleation of deformation twins from the interface. This is suggested to be a new possible twinning mechanism in the dual phase TiAl alloy. The propagation of this deformation twin, or specifically, its interaction with {gamma}-{gamma} and {gamma}-{alpha}{sub 2} interfaces has been discussed. It shows that the {alpha}{sub 2}-lamella is intent to block the propagation of the deformation twin. read less USED (low confidence) L. Wang, X. Liu, and Y. Zhang, “The structure and transport property of liquid Al with different EAM model,” Physica B-condensed Matter. 2004. link Times cited: 4 USED (low confidence) Y. Mishin, “Atomistic modeling of the γ and γ’-phases of the Ni-Al system,” Acta Materialia. 2004. link Times cited: 395 USED (low confidence) H. Guo et al., “Twin junctions with geometric compatibility and mobility in titanium and magnesium,” Scripta Materialia. 2023. link Times cited: 0 USED (low confidence) C. Liu et al., “Strong and ductile nanoscale Ti-1Fe dual-phase alloy via deformation twinning,” Scripta Materialia. 2023. link Times cited: 0 USED (low confidence) R. Fu, Z. Rui, R. Feng, Y. Dong, and X. Lv, “Effects of γ/γ lamellar interfaces on translamellar crack propagation in TiAl alloys,” Journal of Alloys and Compounds. 2022. link Times cited: 2 USED (low confidence) H. Zhang, J. Jeon, F. Rahmani, S. Nouranian, and S. Jiang, “Sintered Ti/Al core/shell nanoparticles: computational investigation of the effects of core volume fraction, heating rate, and room-temperature relaxation on tensile properties,” Journal of Physics D: Applied Physics. 2021. link Times cited: 3 Abstract: Molecular dynamics simulations were performed to roughly imi… read moreAbstract: Molecular dynamics simulations were performed to roughly imitate the conditions of selective laser sintering during additive manufacturing. The role of core volume fraction on the resultant uniaxial tensile properties of sintered Ti/Al bimetallic core/shell nanoparticles (NPs) was investigated during various sintering states. A chain model was created from five single thermally equilibrated Ti/Al NPs with weak neck connections by a solid-state sintering process at room temperature (298 K). The chains were heated to 800 K with two heating rates (0.04 and 0.2 K ps−1), underwent high-temperature relaxation, and were cooled to 298 K with a cooling rate of 0.08 K ps−1. They were then relaxed at 298 K for different periods (i.e. 1, 4, and 10 ns). In a follow-up procedure, those sintered NPs were subjected to uniaxial tension at different strain rates (i.e. 0.001, 0.01, and 0.1% ps−1). The thermodynamic properties and the structural evolutions of atomic configurations were investigated during the sintering process. The tensile responses were also obtained to examine the final product quality. The results indicate a strong correlation between the tensile strength of the final sintered chain product and the Ti core volume fraction. A larger Ti core volume fraction yields a stronger chain structure, resulting in higher tensile strength. The effect of heating rate on the tensile strength of final products with larger core volume fraction is more pronounced. The effect of room-temperature relaxation is not obvious on the tensile strength except for two products, which were sintered with the fast heating rate and tested under the lowest/highest strain rate. Also, high strain rates improve the tensile strength, and low strain rates will lead to enhanced ductility of the final products, especially with residual single atomic chain. read less USED (low confidence) O. Ouadah, G. Merad, and H. Abdelkader, “Atomistic modelling of the γ-TiAl/α2-Ti3Al interfacial properties affected by solutes,” Materials Chemistry and Physics. 2021. link Times cited: 13 USED (low confidence) Y. Tian et al., “Plastic deformation mechanisms of tension-compression asymmetry of nano-polycrystalline tial: Twin boundary spacing and temperature effect,” Computational Materials Science. 2020. link Times cited: 21 USED (low confidence) L. Xiaogang, Y. Zuo, and G. Haiding, “Numerical Simulation of Ti6–Al4–V Alloy Diffusion Bonding Process Based on Molecular Dynamics,” TMS 2019 148th Annual Meeting & Exhibition Supplemental Proceedings. 2019. link Times cited: 0 USED (low confidence) W. Li et al., “Indentation response of γ-TiAl(111) and influence of True-twin interface,” Procedia Manufacturing. 2019. link Times cited: 2 USED (low confidence) Y. Jian, Z. Huang, J. Xing, L. Sun, Y. Liu, and P. Gao, “Phase stability, mechanical properties and electronic structures of Ti Al binary compounds by first principles calculations,” Materials Chemistry and Physics. 2019. link Times cited: 47 USED (low confidence) H. Zheng, B. Li, Y. Tan, G. Li, X. Shu, and P. Peng, “Derivative effect of laser cladding on interface stability of YSZ@Ni coating on GH4169 alloy: An experimental and theoretical study,” Applied Surface Science. 2018. link Times cited: 8 USED (low confidence) 俊一 竹内, 貴宏 河村, 泰之 鈴木, and 具教 北嶋, “分子動力学法を用いた TiAl 系金属間化合物における転位挙動の解析,” Journal of The Japan Institute of Metals. 2015. link Times cited: 0 USED (low confidence) A. Ovrutsky, A. Prokhoda, and M. Rasshchupkyna, “Simulation Techniques for Atomic Systems.” 2014. link Times cited: 3 USED (low confidence) T. Boll and T. Al-Kassab, “Interpretation of atom probe tomography data for the intermetallic TiAl+Nb by means of field evaporation simulation.,” Ultramicroscopy. 2013. link Times cited: 10 USED (low confidence) D. Xu, H. Wang, and R. Yang, “Nucleation and Reaction of Dislocations in Some Metals and Intermetallic Compound TiAl.” 2013. link Times cited: 0 USED (low confidence) R. Voskoboinikov, G. Lumpkin, and S. Middleburgh, “Preferential formation of Al self-interstitial defects in γ-TiAl under irradiation,” Intermetallics. 2013. link Times cited: 14 USED (low confidence) A. Iskandarov, S. Dmitriev, and Y. Umeno, “On Accurate Approach for Molecular Dynamics Study of Ideal Strength at Elevated Temperature,” Journal of Solid Mechanics and Materials Engineering. 2012. link Times cited: 3 Abstract: Influence of temperature on ideal shear strength (ISS), τc, … read moreAbstract: Influence of temperature on ideal shear strength (ISS), τc, of two fcc metals (Al and Cu) was studied by means of molecular dynamics simulations. To get reliable results we investigated influence of parameters of the applied Parrinello-Rahman stress control method and implemented damping of simulation cell fluctuations to avoid occurrence of structural instability assisted by too high fluctuations. The damping successfully reduces strain and stress fluctuations during simulations if the damping factor is specified properly. We also investigated simulation cell size effect to evaluate minimal number of atoms providing reliable results in order to reduce computational efforts and estimate the possibility of applying ab initio calculations. Recently developed embedded atom method (EAM) interatomic potentials for both metals were also examined to find most appropriate for our study. EAM potential developed by Zope et al. and Mishin et al. were revealed to be most suitable for Al and Cu, respectively. It is essential to choose appropriate simulation parameters and interatomic potentials for the valid evaluation of ISS at elevated temperatures. We find almost linear decrease in ideal strength with increasing temperature for [112](111) shear deformation, while critical strain decreases in a nonlinear manner. At room temperature, reduction of shear strength for Al(Cu) is less than 35%(25%) compared to that at 0 K. read less USED (low confidence) Y. Mishin, “Interatomic Potentials for Metals.” 2005. link Times cited: 41 USED (low confidence) Y. Mishin, “Atomistic Computer Simulation of Diffusion.” 2005. link Times cited: 7 NOT USED (low confidence) S. Surulere, M. Shatalov, A. C. Mkolesia, and I. Fedotov, “A Modern Approach for the Identification of the Classical and Modified Generalized Morse Potential.” 2020. link Times cited: 5 Abstract:
This paper proposes an approach for parameter estimation o… read moreAbstract:
This paper proposes an approach for parameter estimation of the Classical and
Generalized Morse Potential functions. A new potential which is a modification of the Generalized
Morse Potential was proposed as parameter estimates yielded complex conjugate roots using gold atom
for simulation.
Existing methods of parameter estimation requires the provision of initial guess values of
which convergence to the optimal solution is not always guaranteed. This makes provision of initial
guess values that guarantees convergence to the optimum solution more of an art than a science. The
proposed objective least squares function method does not require the provision of initial guess values
and it involves the minimization of two formulated objective functions using the differential numerical
approach and least squares method. The built-in “Minimize” function of Mathematica® is also used to
minimize the formulated objective function. Potential energy curves were constructed by fitting
estimated parameter values to experimental data sets of the gold atom using values of the proposed
approach and Mathematica® for performance evaluation. Errors of each constructed potential energy
curves were simulated.
It was observed that the errors were very small for both the Classical and Modified
Generalized Morse Potential.
Hence the approximations of the proposed approach are very good.
read less NOT USED (low confidence) Z. Trautt, F. Tavazza, and C. Becker, “Facilitating the selection and creation of accurate interatomic potentials with robust tools and characterization,” Modelling and Simulation in Materials Science and Engineering. 2015. link Times cited: 14 Abstract: The Materials Genome Initiative seeks to significantly decre… read moreAbstract: The Materials Genome Initiative seeks to significantly decrease the cost and time of development and integration of new materials. Within the domain of atomistic simulations, several roadblocks stand in the way of reaching this goal. While the NIST Interatomic Potentials Repository hosts numerous interatomic potentials (force fields), researchers cannot immediately determine the best choice(s) for their use case. Researchers developing new potentials, specifically those in restricted environments, lack a comprehensive portfolio of efficient tools capable of calculating and archiving the properties of their potentials. This paper elucidates one solution to these problems, which uses Python-based scripts that are suitable for rapid property evaluation and human knowledge transfer. Calculation results are visible on the repository website, which reduces the time required to select an interatomic potential for a specific use case. Furthermore, property evaluation scripts are being integrated with modern platforms to improve discoverability and access of materials property data. To demonstrate these scripts and features, we will discuss the automation of stacking fault energy calculations and their application to additional elements. While the calculation methodology was developed previously, we are using it here as a case study in simulation automation and property calculations. We demonstrate how the use of Python scripts allows for rapid calculation in a more easily managed way where the calculations can be modified, and the results presented in user-friendly and concise ways. Additionally, the methods can be incorporated into other efforts, such as openKIM. read less NOT USED (high confidence) V. Jordan and I. Shmakov, “Recognition of Synthesized Intermetallic Interlayers at the Interface in Ti@Al ‘Core — Shell’ Nanoparticles Based on Computer Molecular-Dynamic Simulation,” Izvestiya of Altai State University. 2023. link Times cited: 0 Abstract: The paper presents the results of applying a new method, pre… read moreAbstract: The paper presents the results of applying a new method, previously developed by the authors, based on precalculated sets of 3D distributions of a matter density. The method is designed to recognize the spatial 3D distributions of the synthesized intermetallic compounds in the volume of a nanoparticle. A set of 3D distributions of a matter density in the volume of a cubic Ti@Al core — shell nanoparticle corresponds to a set of successive time points. It is calculated based on the results of the computer molecular dynamics simulation of self-propagating high temperature synthesis in the nanoparticle. Computational experiments are performed using the LAMMPS software package. Based on the obtained results, thermal and microstructural analyses are performed, confirming the multistage mechanism for the formation of intermetallic phases during the SHS reaction in the Ti-Al reaction medium. The sets of 3D distributions of the matter density and 3D distributions of synthesized intermetallic compounds in the volume of a nanoparticle corresponding to the sequence of time points are calculated. The paper shows the advantage of the method for recognizing 3D distributions of synthesized intermetallic compounds, proposed by the authors, over the methods of similar analysis built into the OVITO software package. read less NOT USED (high confidence) I. Shmakov, “Extension of the functionality of the software for MD-simulation of the SH-synthesis of intermetallides in Ni-Al and Ti-Al nanosystems,” Yugra State University Bulletin. 2022. link Times cited: 0 Abstract: The subject of research: the methodological and functional c… read moreAbstract: The subject of research: the methodological and functional capabilities of specialized software packages of free access LAMMPS and OVITO and author's programs used for simulation of SHS-microkinetics in heterogeneous systems.
Purpose of research: to increase information content, 3D-visualization, and adequate interpretation of the processes of structural-phase transformations at interfaces of the layered, layered-block nanoscale Ni-Al and Ti-Al systems.
Methods and objects of redearch: the molecular dynamics simulation method implemented in the basis of the LAMMPS software package simulates the process of initiation and propagation of the SHS combustion wave in the systems under study, and using the OVITO package, 3D-visualization of the processes of dissolution, diffusion, and motion of the SHS combustion wave front is carried out.
Main results of research: it is shown that the development by the author of software modules for calculating one-dimensional temperature and density profiles of the synthesized material along the direction of combustion wave motion, as well as for calculating and visualizing the 3D-structure of the distribution of synthesized intermetallic interlayers at the interface in nanoparticles with the Ni-Al "core-shell" structure (and similarly for Ti-Al) allows, in contrast to the OVITO package, to detect heterophase intermetallic structures in such systems. As a result of a large series of computational experiments on simulation of microkinetics in the studied nanoscale Ni-Al and Ti-Al systems, it has been established that the software package created by the author with support for parallel computing, which, in addition to the licensed packages LAMMPS and OVITO, integrates author's software modules, has new broader functionality in the methodological aspect of the study of the problems of physical chemistry of the SHS process and is a vivid example of the created software engineering tools in this area of research. read less NOT USED (high confidence) L. Li, T. Gao, Q. Xie, and Z.-an Tian, “Analysis of grain size and five-fold twins during rapid solidification processes inTi3Al alloy,” RSC Advances. 2022. link Times cited: 2 Abstract: The wide application of titanium aluminum (Ti–Al) intermetal… read moreAbstract: The wide application of titanium aluminum (Ti–Al) intermetallic compounds for aerospace and automotive fields has accelerated the research and development of Ti3Al alloy. In this study, simulation is adopted to investigate the crystallization behavior during rapid solidification of Ti3Al alloys using molecular dynamics at different cooling rates of 1010 K s−1, 1011 K s−1, 1012 K s−1, and 1013 K s−1. The evolution of microstructures is characterized by taking advantage of the average potential energy, the pair distribution function and visualization. The results show that the system has formed a microstructural configuration with the face-centered cubic structure as the main structure and the hexagonal close-packed structure as the supplement. An increase in the cooling rate will reduce the grain size of the alloy, which in turn will increase the number of grains. At the cooling rate at which the alloy can crystallize, the system forms five-fold twin structures. Meanwhile, we obtain a deeper insight into the properties of five-fold twins in terms of atoms on different sites, and establish a standard model of the same specification for comparison to get the commonality and differences of the five-fold twins between the standard and the solidified. In addition, the evolution of dislocation densities and distribution of dislocation lines in the system under different conditions are analyzed. This study further explores crystallization behavior on the atomic scale and it is hoped that this research will contribute to expanding the understanding of Ti3Al alloy during the growth process. read less NOT USED (high confidence) Q. Yang and P. Olsson, “Full energy range primary radiation damage model,” Physical Review Materials. 2021. link Times cited: 9 Abstract: A full energy range primary radiation damage model is presen… read moreAbstract: A full energy range primary radiation damage model is presented here. It is based on the athermal recombination corrected displacements per atom (arc-dpa) model but includes a proper treatment of the near threshold conditions for metallic materials. Both ab initio (AIMD) and classical molecular dynamics (MD) simulations are used here for various metals with body-centered cubic (bcc), face-centered cubic (fcc), and hexagonal close-packed (hcp) structures to validate the model. For bcc and hcp metals, the simulation results fit very well with the model. For fcc metals, although there are slight deviations between the model and direct simulation results, it is still a clear improvement on the arc-dpa model. The deviations are due to qualitative differences in the threshold energy surfaces of fcc metals with respect to bcc and hcp metals according to our classical MD simulations. We introduce the minimum threshold displacement energy (TDE) as a term in our damage model. We calculated minimum TDEs for various metal materials using AIMD. In general, the calculated minimum TDEs are in very good agreement with experimental results. Moreover, we noticed a discrepancy in the literature for fcc Ni and estimated the average TDE of Ni using both classical MD and AIMD. It was found that the average TDE of Ni should be \ensuremath{\sim}70 eV based on simulation and experimental data, not the commonly used literature value of 40 eV. The most significant implications of introducing this full energy range damage model will be for estimating the effect of weak particle-matter interactions, such as for \ensuremath{\gamma}- and electron-radiation-induced damage. read less NOT USED (high confidence) O. Ouadah, “Titanium Aluminide Coating: Structural and Elastic Properties by DFT Approach.” 2021. link Times cited: 0 Abstract: The stability, elastic and electronic properties of titanium… read moreAbstract: The stability, elastic and electronic properties of titanium aluminide compounds have been systematically studied by the first-principles calculation. The calculated lattice parameters are consistent with the results found in the literature. The three Ti-Al binary compounds are thermodynamically stable intermetallics depending on their negative formation enthalpy. It has been found that the Ti-Al binary compounds are composed of both metallic and covalent bonds. Elastic properties revealed that these alloys are more resistant to deformation along the a- and c-axis. Besides, the (001)[100] deformation would be easier than (010)[100] deformation for these alloys. The results found in this chapter give a reliable reference for the design of novel Ti-Al binary alloys. read less NOT USED (high confidence) G. Poletaev, A. Sitnikov, and V. Filimonov, “Melting temperature of Ti and TiAl nanoparticles in vacuum and in Al matrix depending on their diameter: molecular dynamics study,” Letters on Materials. 2021. link Times cited: 2 Abstract: The dependence of the melting temperature of Ti and TiAl nan… read moreAbstract: The dependence of the melting temperature of Ti and TiAl nanoparticles on their diameter in vacuum and in Al matrix was studied by the method of molecular dynamics using EAM potentials of Zope and Mishin. Particles with a diameter of 2.5 to 12 nm were considered. The obtained values of the melting point are in good agreement with the approximation curves constructed on the basis that the decrease in the melting temperature is proportional to the ratio of the surface area of the particle to its volume. Wherein the values of the melting temperature of Ti and TiAl particles in the aluminum matrix turned out to be lower than those of particles in vacuum, which is explained by the smearing and disordering of the interface due to mutual diffusion. As the size of particles in vacuum and in aluminum increased, the values of their melting points tended to the same value, which is explained by the decrease in the role of the diffusion-blurred interface with an increase in the particle diameter. The particles began to melt from the surface. The velocity of movement of the melting front depended on temperature and increased with increasing temperature. In the case of particles in aluminum matrix, at temperatures close to the particle melting point, mutual diffusion was significantly accelerated due to melting of the particle boundary layer. Al atoms penetrating into the particle accelerated the movement of the melting front, rapidly occupying the next destroyed layer of the particle. read less NOT USED (high confidence) H. Ganesan, I. Scheider, and C. Cyron, “Quantifying the High-Temperature Separation Behavior of Lamellar Interfaces in γ-Titanium Aluminide Under Tensile Loading by Molecular Dynamics,” Frontiers in Materials. 2021. link Times cited: 4 Abstract: γ-titanium aluminide (TiAl) alloys with fully lamellar micro… read moreAbstract: γ-titanium aluminide (TiAl) alloys with fully lamellar microstructure possess excellent properties for high-temperature applications. Such fully lamellar microstructure has interfaces at different length scales. The separation behavior of the lamellae at these interfaces is crucial for the mechanical properties of the whole material. Unfortunately, quantifying it by experiments is difficult. Therefore, we use molecular dynamics (MD) simulations to this end. Specifically, we study the high-temperature separation behavior under tensile loading of the four different kinds of lamellar interfaces appearing in TiAl, namely, the γ / α 2 , γ / γ PT , γ / γ TT , and γ / γ RB interfaces. In our simulations, we use two different atomistic interface models, a defect-free (Type-1) model and a model with preexisting voids (Type-2). Clearly, the latter is more physical but studying the former also helps to understand the role of defects. Our simulation results show that among the four interfaces studied, the γ / α 2 interface possesses the highest yield strength, followed by the γ / γ PT , γ / γ TT , and γ / γ RB interfaces. For Type-1 models, our simulations reveal failure at the interface for all γ/γ interfaces but not for the γ / α 2 interface. By contrast, for Type-2 models, we observe for all the four interfaces failure at the interface. Our atomistic simulations provide important data to define the parameters of traction–separation laws and cohesive zone models, which can be used in the framework of continuum mechanical modeling of TiAl. Temperature-dependent model parameters were identified, and the complete traction–separation behavior was established, in which interface elasticity, interface plasticity, and interface damage could be distinguished. By carefully eliminating the contribution of bulk deformation from the interface behavior, we were able to quantify the contribution of interface plasticity and interface damage, which can also be related to the dislocation evolution and void nucleation in the atomistic simulations. read less NOT USED (high confidence) H. Bhattarai, K. E. Newman, and J. Gezelter, “The role of polarizability in the interfacial thermal conductance at the gold-water interface.,” The Journal of chemical physics. 2020. link Times cited: 3 Abstract: We have studied the interfacial thermal conductance, G, of t… read moreAbstract: We have studied the interfacial thermal conductance, G, of the flat Au(111)-water interface using non-equilibrium molecular dynamics simulations. We utilized two metal models, one based on the embedded atom method (EAM) and the other including metallic polarizability via a density readjusting EAM. These were combined with three popular water models, SPC/E, TIP4P, and TIP4P-FQ, to understand the role of polarizability in the thermal transport process. A thermal flux was introduced using velocity shearing and scaling reverse non-equilibrium molecular dynamics, and transport coefficients were measured by calculating the resulting thermal gradients and temperature differences at the interface. Our primary finding is that the computed interfacial thermal conductance between a bare metal interface and water increases when polarizability is taken into account in the metal model. Additional work to understand the origin of the conductance difference points to changes in the local ordering of the water molecules in the first two layers of water above the metal surface. Vibrational densities of states on both sides of the interface exhibit interesting frequency modulation close to the surface but no obvious differences due to metal polarizability. read less NOT USED (high confidence) E. Salamatov and E. Dolgusheva, “The Role of Long‐Wave Bending Vibrations in the Destruction of Ultrathin Al Films,” physica status solidi (b). 2020. link Times cited: 1 Abstract: The molecular dynamics method is used to study the process o… read moreAbstract: The molecular dynamics method is used to study the process of development of dynamic instability of a thin film, leading to its destruction. The calculations are performed for a thin aluminum film using the interatomic interaction potential tested by comparing the numerical results with the analytical ones from the elasticity theory. An original approach which allows one to calculate the dispersion law of long‐wave phonons in ultrathin films is developed. The temperatures (<600 K) at which the system remains stable for 0.6 ns are found. This makes it possible to analyze the low‐frequency part of the spectrum down to the minimum frequency νmin = 0.0166 THz, and to determine the vibration frequency of the longest bending wave ν0 = 0.033 THz which decreases with increasing temperature, and therefore, its period grows. Once the vibration period becomes comparable with the time of simulation, there occurs a continuous increase in the amplitude of this mode which will be referred to as “retarded mode.” It is shown that the film destruction begins with the attainment of a certain critical value of the bending wave amplitude. read less NOT USED (high confidence) Z. Yin et al., “Phase stability, brittle-ductile transition, and electronic structures of the TiAl alloying with Fe, Ru, Ge, and Sn: a first-principle investigation,” Journal of Molecular Modeling. 2020. link Times cited: 5 NOT USED (high confidence) K. Kowalczyk-Gajewska and M. Ma’zdziarz, “Elastic properties of nanocrystalline materials of hexagonal symmetry: The core-shell model and atomistic estimates,” International Journal of Engineering Science. 2020. link Times cited: 5 NOT USED (high confidence) D. R. Pratt, L. Morrissey, and S. Nakhla, “Molecular dynamics simulations of nanoindentation – the importance of force field choice on the predicted elastic modulus of FCC aluminum,” Molecular Simulation. 2020. link Times cited: 5 Abstract: ABSTRACT Molecular Dynamics (MD) was used to determine the a… read moreAbstract: ABSTRACT Molecular Dynamics (MD) was used to determine the accuracy of different force fields on predicting the elastic modulus of single crystal aluminum through nanoindentation tests. In this work, nanoindentation was performed using three different types of force fields (EAM, MEAM and ReaxFF) and the resulting elastic modulus was compared to the value obtained using elastic constants from standard small strain tensile simulations. When the predicted modulus of each force field was compared to the modulus via elastic constants, the ReaxFF resultant moduli were similar to that of nanoindentation, but for EAM and MEAM the two methods produced significantly different values. Therefore, even if a force field is parameterised for elastic modulus, it does not guarantee the force field will accurately predict the modulus from other procedures. As well, two different methods for calculating modulus from indentation curves were compared: The Hertz approximation and the Oliver and Pharr (O&P) method. For EAM and MEAM force fields, the Hertz method significantly under predicted modulus while the O&P method was in better agreement with the experimental modulus. read less NOT USED (high confidence) J. Chen, W. Chen, and C. Wang, “Modeling and investigation for atomic diffusion and mechanical properties of TiAl/Ti3Al interface: temperature effect,” Applied Physics A. 2020. link Times cited: 5 NOT USED (high confidence) E. Antillon and M. Ghazisaeidi, “Efficient determination of solid-state phase equilibrium with the multicell Monte Carlo method.,” Physical review. E. 2020. link Times cited: 5 Abstract: Building on our previously introduced multicell Monte Carlo … read moreAbstract: Building on our previously introduced multicell Monte Carlo (MC)^{2} method for modeling phase coexistence, this paper provides important improvements for efficient determination of phase equilibria in solids. The (MC)^{2} method uses multiple cells, representing possible phases. Mass transfer between cells is modeled virtually by solving the mass balance equation after the composition of each cell is changed arbitrarily. However, searching for the minimum free energy during this process poses a practical problem. The solution to the mass balance equation is not unique away from equilibrium, and consequently the algorithm is in risk of getting trapped in nonequilibrium solutions. Therefore, a proper stopping condition for (MC)^{2} is currently lacking. In this work, we introduce a consistency check via a predictor-corrector algorithm to penalize solutions that do not satisfy a necessary condition for equivalence of chemical potentials and steer the system toward finding equilibrium. The most general acceptance criteria for (MC)^{2} is derived starting from the isothermal-isobaric Gibbs ensemble for mixtures. Using this ensemble, translational MC moves are added to include vibrational excitations as well as volume MC moves to ensure the condition of constant pressure and temperature entirely with a MC approach, without relying on any other method for relaxation of these degrees of freedom. As a proof of concept the method is applied to two binary alloys with miscibility gaps and a model quaternary alloy, using classical interatomic potentials. read less NOT USED (high confidence) L.-F. Lai, D. Lu, K.-S. Hsu, and J.-M. Lu, “A Study of Nanoscale Vanadium Powder Applied on 3D Printing Process,” 2019 IEEE 2nd International Conference on Knowledge Innovation and Invention (ICKII). 2019. link Times cited: 0 Abstract: The molecular dynamics simulation method is utilized to inve… read moreAbstract: The molecular dynamics simulation method is utilized to investigate the physical characteristics of nanoscale vanadium powder during 3D printing powder bed fusion laser sintering process. The radius of gyration, neck width, and root mean square of different powder size of nanoscale vanadium powder during 3D printing laser sintering process under different heating rate is analyzed and discussed. The neck width and internal lattice changes are also observed.It is observed that the temperature of solid state diffusion decrease with heating rate increasing, but the temperature of that increase with powder size decreasing. It is found that the coalescence temperature of nanoscale vanadium powder is range of between 1600K and 1950K, and the melting temperature of that is range of between 1850K and 1990K. read less NOT USED (high confidence) R. Voskoboinikov, “Radiation Defects in Aluminum: MD Simulations of Collision Cascades in the Bulk of Material,” Physics of Metals and Metallography. 2019. link Times cited: 11 NOT USED (high confidence) Q. J. Li, H. Sheng, and E. Ma, “Strengthening in multi-principal element alloys with local-chemical-order roughened dislocation pathways,” Nature Communications. 2019. link Times cited: 389 NOT USED (high confidence) L. Zhang, Y. Shibuta, X. Huang, C. Lu, and M. Liu, “Grain boundary induced deformation mechanisms in nanocrystalline Al by molecular dynamics simulation: From interatomic potential perspective,” Computational Materials Science. 2019. link Times cited: 39 NOT USED (high confidence) C. Fang and Z. Fan, “An ab initio study on stacking and stability of TiAl3 phases,” Computational Materials Science. 2018. link Times cited: 8 NOT USED (high confidence) L. Hale, “Comparing Modeling Predictions of Aluminum Edge Dislocations: Semidiscrete Variational Peierls–Nabarro Versus Atomistics,” JOM. 2018. link Times cited: 7 NOT USED (high confidence) K. Dang, L. Capolungo, and D. Spearot, “Nanoscale dislocation shear loops at static equilibrium and finite temperature,” Modelling and Simulation in Materials Science and Engineering. 2017. link Times cited: 14 Abstract: Atomistic simulations are used to determine the resolved she… read moreAbstract: Atomistic simulations are used to determine the resolved shear stress necessary for equilibrium and the resulting geometry of nanoscale dislocation shear loops in Al. Dislocation loops with different sizes and shapes are created via superposition of elemental triangular dislocation displacement fields in the presence of an externally imposed shear stress. First, a bisection algorithm is developed to determine systematically the resolved shear stress necessary for equilibrium at 0 K. This approach allows for the identification of dislocation core structure and a correlation between dislocation loop size, shape and the computed shear stress for equilibrium. It is found, in agreement with predictions made by Scattergood and Bacon, that the equilibrium shape of a dislocation loop becomes more circular with increasing loop size. Second, the bisection algorithm is extended to study the influence of temperature on the resolved shear stress necessary for stability. An approach is presented to compute the effective lattice friction stress, including temperature dependence, for dislocation loops in Al. The temperature dependence of the effective lattice friction stress can be reliably computed for dislocation loops larger than 16.2 nm. However, for dislocation loops smaller than this threshold, the effective lattice friction stress shows a dislocation loop size dependence caused by significant overlap of the stress fields on the interior of the dislocation loops. Combined, static and finite temperature atomistic simulations provide essential data to parameterize discrete dislocation dynamics simulations. read less NOT USED (high confidence) P. Dumitraschkewitz, H. Clemens, S. Mayer, and D. Holec, “Impact of Alloying on Stacking Fault Energies in γ-TiAl,” Applied Sciences. 2017. link Times cited: 20 Abstract: Microstructure and mechanical properties are key parameters … read moreAbstract: Microstructure and mechanical properties are key parameters influencing the performance of structural multi-phase alloys such as those based on intermetallic TiAl compounds. There, the main constituent, a γ -TiAl phase, is derived from a face-centered cubic structure. Consequently, the dissociation of dislocations and generation of stacking faults (SFs) are important factors contributing to the overall deformation behavior, as well as mechanical properties, such as tensile/creep strength and, most importantly, fracture elongation below the brittle-to-ductile transition temperature. In this work, SFs on the { 111 ) plane in γ -TiAl are revisited by means of ab initio calculations, finding their energies in agreement with previous reports. Subsequently, stacking fault energies are evaluated for eight ternary additions, namely group IVB–VIB elements, together with Ti off-stoichiometry. It is found that the energies of superlattice intrinsic SFs, anti-phase boundaries (APBs), as well as complex SFs decrease by 20–40% with respect to values in stoichiometric γ -TiAl once an alloying element X is present in the fault plane having thus a composition of Ti-50Al-12.5X. In addition, Mo, Ti and V stabilize the APB on the (111) plane, which is intrinsically unstable at 0 K in stoichiometric γ -TiAl. read less NOT USED (high confidence) T. He et al., “Inflating hollow nanocrystals through a repeated Kirkendall cavitation process,” Nature Communications. 2017. link Times cited: 114 NOT USED (high confidence) A. Mayer and A. A. Ebel, “Shock-induced compaction of nanoparticle layers into nanostructured coating,” Journal of Applied Physics. 2017. link Times cited: 16 Abstract: A new process of shock wave consolidation of nanoparticles i… read moreAbstract: A new process of shock wave consolidation of nanoparticles into a nanocrystalline coating is theoretically considered. In the proposed scheme, the nanoparticle layers, which are attached to the substrate surface by adhesion, are compacted by plane ultra-short shock waves coming from the substrate. The initial adhesion is self-arisen at any contact between the nanoparticles without a pre-compression. The absence of the nanoparticle ejections due to the shock wave action is connected with the strong adhesive forces, which allow nanoparticles to be attached to each other and to substrate while they are being compacted; this should be valid for small enough nanoparticles. Severe plastic deformation of the nanoparticles and the increased temperature due to collapse of voids between them facilitate their compaction into the monolithic nanocrystalline layer. We consider the examples of Cu and Ni nanoparticles on Al substrate using molecular dynamic simulations. We show the efficiency of the action of multiple sh... read less NOT USED (high confidence) A. Takahashi, A. Seko, and I. Tanaka, “Linearized machine-learning interatomic potentials for non-magnetic elemental metals: Limitation of pairwise descriptors and trend of predictive power.,” The Journal of chemical physics. 2017. link Times cited: 20 Abstract: Machine-learning interatomic potential (MLIP) has been of gr… read moreAbstract: Machine-learning interatomic potential (MLIP) has been of growing interest as a useful method to describe the energetics of systems of interest. In the present study, we examine the accuracy of linearized pairwise MLIPs and angular-dependent MLIPs for 31 elemental metals. Using all of the optimal MLIPs for 31 elemental metals, we show the robustness of the linearized frameworks, the general trend of the predictive power of MLIPs, and the limitation of pairwise MLIPs. As a result, we obtain accurate MLIPs for all 31 elements using the same linearized framework. This indicates that the use of numerous descriptors is the most important practical feature for constructing MLIPs with high accuracy. An accurate MLIP can be constructed using only pairwise descriptors for most non-transition metals, whereas it is very important to consider angular-dependent descriptors when expressing interatomic interactions of transition metals. read less NOT USED (high confidence) S. Alkan and H. Sehitoglu, “Dislocation core effects on slip response of NiTi- a key to understanding shape memory,” International Journal of Plasticity. 2017. link Times cited: 32 NOT USED (high confidence) A. Takahashi, A. Seko, and I. Tanaka, “Conceptual and practical bases for the high accuracy of machine learning interatomic potential,” arXiv: Materials Science. 2017. link Times cited: 29 Abstract: Machine learning interatomic potentials (MLIPs) based on a l… read moreAbstract: Machine learning interatomic potentials (MLIPs) based on a large dataset obtained by density functional theory (DFT) calculation have been developed recently. This study gives both conceptual and practical bases for the high accuracy of MLIPs, although MLIPs have been considered to be simply an accurate black-box description of atomic energy. We also construct the most accurate MLIP of the elemental Ti ever reported using a linearized MLIP framework and many angular-dependent descriptors, which also corresponds to a generalization of the modified embedded atom method (MEAM) potential. read less NOT USED (high confidence) M. Kbirou, S. Trady, A. Hasnaoui, and M. Mazroui, “Cooling rate dependence and local structure in aluminum monatomic metallic glass,” Philosophical Magazine. 2017. link Times cited: 39 Abstract: The local atomic structure in aluminium monatomic metallic g… read moreAbstract: The local atomic structure in aluminium monatomic metallic glass is studied using molecular dynamics simulations combined with the embedded atom method (EAM). We have used a variety of analytical methods to characterise the atomic configurations of our system: the Pair Distribution Function (PDF), the Common Neighbour Analysis (CNA) and the Voronoi Tessellation Analysis. CNA was used to investigate the order change from liquid to amorphous phases, recognising that the amount of icosahedral clusters increases with the decrease of temperature. The Voronoi analysis revealed that the icosahedral-like polyhedral are the predominant ones. It has been observed that the PDF function shows a splitting in the second peak, which cannot be attributed to the only ideal icosahedral polyhedron 〈0, 0, 12, 0〉, but also to the formation of other Voronoi polyhedra 〈0, 1, 10, 2〉 . Further, the PDFs were then integrated giving the cumulative coordination number in order to compute the fractal dimension (df). read less NOT USED (high confidence) J. Yang, X. Wang, B. Cao, Y. Wu, K. Zhang, and R. Hu, “Tailoring the Microstructure of a β-Solidifying TiAl Alloy by Controlled Post-solidification Isothermal Holding and Cooling,” Metallurgical and Materials Transactions A. 2017. link Times cited: 30 NOT USED (high confidence) B. Syed et al., “Morphology and microstructure evolution of Ti-50 at.% Al cathodes during cathodic arc deposition of Ti-Al-N coatings,” Journal of Applied Physics. 2017. link Times cited: 12 Abstract: Today's research on the cathodic arc deposition techniq… read moreAbstract: Today's research on the cathodic arc deposition technique and coatings therefrom primarily focuses on the effects of, e.g., nitrogen partial pressure, growth temperature, and substrate bias. Detailed studies on the morphology and structure of the starting material—the cathode—during film growth and its influence on coating properties at different process conditions are rare. This work aims to study the evolution of the converted layer, its morphology, and microstructure, as a function of the cathode material grain size during deposition of Ti-Al-N coatings. The coatings were reactively grown in pure N2 discharges from powder metallurgically manufactured Ti-50 at.% Al cathodes with grain size distribution averages close to 1800, 100, 50, and 10 μm, respectively, and characterized with respect to microstructure, composition, and mechanical properties. The results indicate that for the cathode of 1800 μm grain size the disparity in the work function among parent phases plays a dominant role in the pronounced... read less NOT USED (high confidence) Y. Jiang, J. Luo, and Y. Wu, “The validation and preference among different EAM potentials to describe the solid–liquid transition of aluminum,” Modelling and Simulation in Materials Science and Engineering. 2017. link Times cited: 6 Abstract: Empirical potential is vital to the classic atomic simulatio… read moreAbstract: Empirical potential is vital to the classic atomic simulation, especially for the study of phase transitions, as well as the solid-interface. In this paper, we attempt to set up a uniform procedure for the validation among different potentials before the formal simulation study of phase transitions of metals. Two main steps are involved: (1) the prediction of the structures of both solid and liquid phases and their mutual transitions, i.e. melting and crystallization; (2) the prediction of vital thermodynamic (the equilibrium melting point at ambient pressure) and dynamic properties (the degrees of superheating and undercooling). We applied this procedure to the testing of seven published embedded-atom potentials (MKBA (Mendelev et al 2008 Philos. Mag. 88 1723), MFMP (Mishin et al 1999 Phys. Rev. B 59 3393), MDSL (Sturgeon and Laird 2000 Phys. Rev. B 62 14720), ZM (Zope and Mishin 2003 Phys. Rev. B 68 024102), LEA (Liu et al 2004 Model. Simul. Mater. Sci. Eng. 12 665), WKG (Winey et al 2009 Model. Simul. Mater. Sci. Eng. 17 055004) and ZJW (Zhou et al 2004 Phys. Rev. B 69 144113)) for the description of the solid–liquid transition of Al. All the predictions of structure, melting point and superheating/undercooling degrees were compared with the experiments or theoretical calculations. Then, two of them, MKBA and MDSL, were proven suitable for the study of the solid–liquid transition of Al while the residuals were unqualified. However, potential MKBA is more accurate to predict the structures of solid and liquid, while MDSL works a little better in the thermodynamic and dynamic predictions of solid–liquid transitions. read less NOT USED (high confidence) Y.-hua Zhou, R. Smith, S. Kenny, and A. L. Lloyd, “Development of an empirical interatomic potential for the Ag–Ti system,” Nuclear Instruments & Methods in Physics Research Section B-beam Interactions With Materials and Atoms. 2017. link Times cited: 5 NOT USED (high confidence) M. Mendelev, T. L. Underwood, and G. Ackland, “Development of an interatomic potential for the simulation of defects, plasticity, and phase transformations in titanium.,” The Journal of chemical physics. 2016. link Times cited: 122 Abstract: New interatomic potentials describing defects, plasticity, a… read moreAbstract: New interatomic potentials describing defects, plasticity, and high temperature phase transitions for Ti are presented. Fitting the martensitic hcp-bcc phase transformation temperature requires an efficient and accurate method to determine it. We apply a molecular dynamics method based on determination of the melting temperature of competing solid phases, and Gibbs-Helmholtz integration, and a lattice-switch Monte Carlo method: these agree on the hcp-bcc transformation temperatures to within 2 K. We were able to develop embedded atom potentials which give a good fit to either low or high temperature data, but not both. The first developed potential (Ti1) reproduces the hcp-bcc transformation and melting temperatures and is suitable for the simulation of phase transitions and bcc Ti. Two other potentials (Ti2 and Ti3) correctly describe defect properties and can be used to simulate plasticity or radiation damage in hcp Ti. The fact that a single embedded atom method potential cannot describe both low and high temperature phases may be attributed to neglect of electronic degrees of freedom, notably bcc has a much higher electronic entropy. A temperature-dependent potential obtained from the combination of potentials Ti1 and Ti2 may be used to simulate Ti properties at any temperature. read less NOT USED (high confidence) Q. J. Li, J. Li, Z. Shan, and E. Ma, “Strongly correlated breeding of high-speed dislocations,” Acta Materialia. 2016. link Times cited: 22 NOT USED (high confidence) S. Trady, A. Hasnaoui, M. Mazroui, and K. Saadouni, “Local atomic structures of single-component metallic glasses,” The European Physical Journal B. 2016. link Times cited: 21 NOT USED (high confidence) G. Ren and H. Sehitoglu, “Interatomic potential for the NiTi alloy and its application,” Computational Materials Science. 2016. link Times cited: 45 NOT USED (high confidence) R. Rozas, Demi̇rag A., P. Toledo, and J. Horbach, “Thermophysical properties of liquid Ni around the melting temperature from molecular dynamics simulation,” Journal of Chemical Physics. 2016. link Times cited: 17 Abstract: Thermophysical properties of liquid nickel (Ni) around the m… read moreAbstract: Thermophysical properties of liquid nickel (Ni) around the melting temperature are investigated by means of classical molecular dynamics (MD) simulation, using three different embedded atom method potentials to model the interactions between the Ni atoms. Melting temperature, enthalpy, static structure factor, self-diffusion coefficient, shear viscosity, and thermal diffusivity are compared to recent experimental results. Using ab initio MD simulation, we also determine the static structure factor and the mean-squared displacement at the experimental melting point. For most of the properties, excellent agreement is found between experiment and simulation, provided the comparison relative to the corresponding melting temperature. We discuss the validity of the Hansen-Verlet criterion for the static structure factor as well as the Stokes-Einstein relation between self-diffusion coefficient and shear viscosity. The thermal diffusivity is extracted from the autocorrelation function of a wavenumber-dependent temperature fluctuation variable. read less NOT USED (high confidence) J. Michalka, A. P. Latham, and J. Gezelter, “CO-Induced Restructuring on Stepped Pt Surfaces: A Molecular Dynamics Study,” Journal of Physical Chemistry C. 2016. link Times cited: 7 Abstract: The effects of plateau width and step-edge kinking on carbon… read moreAbstract: The effects of plateau width and step-edge kinking on carbon monoxide (CO)-induced restructuring of platinum surfaces were explored using molecular dynamics (MD) simulations. Platinum crystals displaying four different vicinal surfaces [(321), (765), (112), and (557)] were constructed and exposed to partial coverages of carbon monoxide. Platinum–CO interactions were fit to recent experimental data and density functional theory (DFT) calculations, providing a classical interaction model that captures the atop binding preference on Pt. The differences in Pt–Pt binding strength between edge atoms on the various facets were found to play a significant role in step-edge wandering and reconstruction events. Because the mechanism for step doubling relies on a stochastic meeting of two wandering edges, the widths of the plateaus on the original surfaces were also found to play a role in these reconstructions. On the Pt(321) surfaces, the CO adsorbate was found to assist in reordering the kinked step edges into st... read less NOT USED (high confidence) P. Chowdhury, L. Patriarca, G. Ren, and H. Sehitoglu, “Molecular dynamics modeling of NiTi superelasticity in presence of nanoprecipitates,” International Journal of Plasticity. 2016. link Times cited: 74 NOT USED (high confidence) Gui-Jun 贵钧 Cheng 程, B. Fu 付, Q. Hou 侯, X. Zhou 周, and Jun 俊 Wang 汪, “Diffusion behavior of helium in titanium and the effect of grain boundaries revealed by molecular dynamics simulation,” Chinese Physics B. 2016. link Times cited: 11 Abstract: The microstructures of titanium (Ti), an attractive tritium … read moreAbstract: The microstructures of titanium (Ti), an attractive tritium (T) storage material, will affect the evolution process of the retained helium (He). Understanding the diffusion behavior of He at the atomic scale is crucial for the mechanism of material degradation. The novel diffusion behavior of He has been reported by molecular dynamics (MD) simulation for the bulk hcp-Ti system and the system with grain boundary (GB). It is observed that the diffusion of He in the bulk hcp-Ti is significantly anisotropic (the diffusion coefficient of the [0001] direction is higher than that of the basal plane), as represented by the different migration energies. Different from convention, the GB accelerates the diffusion of He in one direction but not in the other. It is observed that a twin boundary (TB) can serve as an effective trapped region for He. The TB accelerates diffusion of He in the direction perpendicular to the twinning direction (TD), while it decelerates the diffusion in the TD. This finding is attributable to the change of diffusion path caused by the distortion of the local favorable site for He and the change of its number in the TB region. read less NOT USED (high confidence) G. P. P. Pun, V. Yamakov, and Y. Mishin, “Interatomic potential for the ternary Ni–Al–Co system and application to atomistic modeling of the B2–L10 martensitic transformation,” Modelling and Simulation in Materials Science and Engineering. 2015. link Times cited: 80 Abstract: Ni–Al–Co is a promising system for ferromagnetic shape memor… read moreAbstract: Ni–Al–Co is a promising system for ferromagnetic shape memory applications. This paper reports on the development of a ternary embedded-atom potential for this system by fitting to experimental and first-principles data. Reasonably good agreement is achieved for physical properties between values predicted by the potential and values known from experiment and/or first-principles calculations. The potential reproduces basic features of the martensitic phase transformation from the B2-ordered high-temperature phase to a tetragonal CuAu-ordered low-temperature phase. The compositional and temperature ranges of this transformation and the martensite microstructure predicted by the potential compare well with existing experimental data. These results indicate that the proposed potential can be used for simulations of the shape memory effect in the Ni–Al–Co system. read less NOT USED (high confidence) R. Tanaka, K. Takeuchi, and K. Yuge, “Application of Grid Increment Cluster Expansion to Modeling Potential Energy Surface of Cu-Based Alloys,” Materials Transactions. 2015. link Times cited: 3 Abstract: We demonstrate the applicability of extended cluster expansi… read moreAbstract: We demonstrate the applicability of extended cluster expansion technique, GICE, to calculation of a potential energy surface (PES) at discrete position in terms of atomic arrangement with an example of Cu and Cu-Ti binary system on fcc lattice. We find that the proposed CE successfully predicts total energy within error of 0.5meV/atom for Cu and 1.2meV/atom for Cu-Ti with respect to DFT calculation, which indicates that this method can model the PES and possesses potential to formulate physical properties in terms of atomic arrangement. [doi:10.2320/matertrans.M2015024] read less NOT USED (high confidence) A. Bakulin, S. Kulkova, Q. Hu, and R. Yang, “Theoretical study of oxygen sorption and diffusion in the volume and on the surface of a γ-TiAl alloy,” Journal of Experimental and Theoretical Physics. 2015. link Times cited: 16 NOT USED (high confidence) K. Choudhary et al., “Charge optimized many-body potential for aluminum,” Journal of Physics: Condensed Matter. 2014. link Times cited: 19 Abstract: An interatomic potential for Al is developed within the thir… read moreAbstract: An interatomic potential for Al is developed within the third generation of the charge optimized many-body (COMB3) formalism. The database used for the parameterization of the potential consists of experimental data and the results of first-principles and quantum chemical calculations. The potential exhibits reasonable agreement with cohesive energy, lattice parameters, elastic constants, bulk and shear modulus, surface energies, stacking fault energies, point defect formation energies, and the phase order of metallic Al from experiments and density functional theory. In addition, the predicted phonon dispersion is in good agreement with the experimental data and first-principles calculations. Importantly for the prediction of the mechanical behavior, the unstable stacking fault energetics along the direction on the (1 1 1) plane are similar to those obtained from first-principles calculations. The polycrsytal when strained shows responses that are physical and the overall behavior is consistent with experimental observations. read less NOT USED (high confidence) X.-Y. Sun, Y. Xu, G.-K. Xu, and J.-hui Zhang, “Effects of interface cohesion on mechanical properties of interpenetrating phase nanocomposites,” Micro & Nano Letters. 2014. link Times cited: 4 Abstract: Molecular dynamics simulations and micromechanics model anal… read moreAbstract: Molecular dynamics simulations and micromechanics model analysis are performed to investigate the mechanical behaviours and interfacial effects of interpenetrating phase composites in the nanoscale. It is observed that the overall Young's modulus and ultimate strength of the nanocomposites vary nonlinearly with the cohesive energy of the interface. The cohesive properties affect the stiffness of the interface zone, and in turn, influence the effective Young's modulus of composites. The competition between interfacial failure and weak phase damage results in an optimal cohesive parameter of the interface, at which the composite possesses the maximal ultimate strength. The obtained results provide useful guidelines for the design and optimisation of advanced nanocomposites with superior mechanical properties. read less NOT USED (high confidence) H. Wang, D. Xu, and R. Yang, “Defect clustering upon dislocation annihilation in α-titanium and α-zirconium with hexagonal close-packed structure,” Modelling and Simulation in Materials Science and Engineering. 2014. link Times cited: 5 Abstract: The annihilation of vacancy- and interstitial-type dislocati… read moreAbstract: The annihilation of vacancy- and interstitial-type dislocation dipoles is investigated employing atomistic simulations and metadynamics in hexagonal close-packed (hcp) metals α-titanium and α-zirconium, with a variety of dipole heights, orientations and annealing temperatures. Molecular dynamics simulations reveal that depending on the dipole type, height, orientation, etc., dipolar configurations transform into specific reconstructed configurations at low temperature, while vacancy or interstitial clustering occurs at high temperature. The time of clustering and the lifetime of the resulting clusters are estimated through the search of the lowest-energy paths. Compared with previous knowledge on face-centered cubic (fcc) metals, the general processes of dislocation annihilation and point defect clustering are similar, however, due to the varied lattice symmetry: (1) the atomic structures of the reconstructed configurations at low temperature and the clusters at high temperature in hcp systems are different from those in fcc systems; and (2) in hcp systems the clustering process is shortened and the stability of the resulting clusters is enhanced compared with fcc systems. read less NOT USED (high confidence) X.-Y. Sun, R. Wu, R. Xia, and Y. Xu, “Blister formation in graphene coating on the nanoparticle decorated copper surface,” RSC Advances. 2014. link Times cited: 3 Abstract: Embedded nanoparticles between a graphene coating and substr… read moreAbstract: Embedded nanoparticles between a graphene coating and substrate often precipitate blisters generated in graphene, which may impede the application of graphene as a surface coating. Molecular dynamics (MD) simulations are performed to analyze the evolution of nanocoating morphology during the process of adhering the graphene onto a nanoparticle decorated metal surface. The simulation reveals that for a deformable nanoparticle, a blister rudiment with a tail formed and then changes into an irregular blister, but a rigid nanoparticle will be ejected from the surface of the substrate without any blistering. Substrate damage caused by the nanoparticles during coating is also analyzed. It is found that hexagonal close-packed atoms emerge from the contact point between the rigid particle and substrate. Understanding how blisters form in graphene coatings by an atomic-scale approach will help this promising material function more effectively and widely. read less NOT USED (high confidence) S. Kiselev, “Method of molecular dynamics in mechanics of deformable solids,” Journal of Applied Mechanics and Technical Physics. 2014. link Times cited: 8 NOT USED (high confidence) S. Kiselev, “Method of molecular dynamics in mechanics of deformable solids,” Journal of Applied Mechanics and Technical Physics. 2014. link Times cited: 1 NOT USED (high confidence) D. Belashchenko, “Computer simulation of liquid metals,” Physics—Uspekhi. 2013. link Times cited: 84 Abstract: Methods for and the results of the computer simulation of li… read moreAbstract: Methods for and the results of the computer simulation of liquid metals are reviewed. Two basic methods, classical molecular dynamics with known interparticle potentials and the ab initio method, are considered. Most attention is given to the simulated results obtained using the embedded atom model (EAM). The thermodynamic, structural, and diffusion properties of liquid metal models under normal and extreme (shock) pressure conditions are considered. Liquid-metal simulated results for the Groups I–IV elements, a number of transition metals, and some binary systems (Fe–C, Fe–S) are examined. Possibilities for the simulation to account for the thermal contribution of delocalized electrons to energy and pressure are considered. Solidification features of supercooled metals are also discussed. read less NOT USED (high confidence) J.-Q. Ren, Q. Sun, L. Xiao, X. Ding, and J. Sun, “Molecular dynamics simulations of the size effect of titanium single-crystal nanopillars orientated for double prismatic slips,” Philosophical Magazine Letters. 2013. link Times cited: 9 Abstract: An inverse “smaller is stronger” trend is predicted on the b… read moreAbstract: An inverse “smaller is stronger” trend is predicted on the basis of molecular dynamics simulations of α-titanium (Ti) single-crystal nanopillars orientated for double prismatic slips when the nanopillars are less than 7 nm wide. This trend is attributed to a significant increase in the surface energy due to the nucleation and propagation of edge dislocations on the surface of the pillars. read less NOT USED (high confidence) W. Setyawan et al., “Asymmetry of radiation damage properties in Al–Ti nanolayers,” Journal of Nuclear Materials. 2013. link Times cited: 9 NOT USED (high confidence) N. Tsakiris and L. J. Lewis, “Phase diagram of aluminum from EAM potentials,” The European Physical Journal B. 2013. link Times cited: 2 NOT USED (high confidence) C. J. Aas, L. Szunyogh, R. Evans, and R. Chantrell, “Effect of stacking faults on the magnetocrystalline anisotropy of hcp Co: a first-principles study,” Journal of Physics: Condensed Matter. 2013. link Times cited: 16 Abstract: In terms of the fully relativistic screened Korringa–Kohn–Ro… read moreAbstract: In terms of the fully relativistic screened Korringa–Kohn–Rostoker method we investigate the effect of stacking faults on the magnetic properties of hexagonal close-packed (hcp) cobalt. In particular, we consider the formation energy and the effect on the magnetocrystalline anisotropy energy (MAE) of four different stacking faults in hcp cobalt—an intrinsic growth fault, an intrinsic deformation fault, an extrinsic fault and a twin-like fault. We find that the intrinsic growth fault has the lowest formation energy, in good agreement with previous first-principles calculations. With the exception of the intrinsic deformation fault which has a positive impact on the MAE, we find that the presence of a stacking fault generally reduces the MAE of bulk Co. Finally, we consider a pair of intrinsic growth faults and find that their effect on the MAE is not additive, but synergic. read less NOT USED (high confidence) H. Wang, D. Xu, D. Rodney, P. Veyssiére, and R. Yang, “Atomistic investigation of the annihilation of non-screw dislocation dipoles in Al, Cu, Ni and γ-TiAl,” Modelling and Simulation in Materials Science and Engineering. 2013. link Times cited: 19 Abstract: Annihilation of vacancy-type non-screw dipolar dislocations … read moreAbstract: Annihilation of vacancy-type non-screw dipolar dislocations is studied with molecular dynamics in fcc metals Al, Cu and Ni, and intermetallic γ-TiAl. Contrary to common belief, dipoles do not simply disappear. Instead, they transform into a series of defects depending on their height, orientation and temperature. At low temperatures, hollow structures, reconstructed configurations and faulted dipoles are formed. At high temperatures, with the help of short-range diffusion, isolated or interconnected vacancy clusters and stacking-fault tetrahedra are formed within a simulation time of 1 ns. Employing saddle-point-search methods, the formation of the above by-products is explained by accelerated diffusion paths along the dipole cores. read less NOT USED (high confidence) M. Benoit, N. Tarrat, and J. Morillo, “Density functional theory investigations of titanium γ-surfaces and stacking faults,” Modelling and Simulation in Materials Science and Engineering. 2012. link Times cited: 40 Abstract: Bulk properties of hcp-Ti, relevant for the description of d… read moreAbstract: Bulk properties of hcp-Ti, relevant for the description of dislocations, such as elastic constants, stacking faults and γ-surface, are computed using density functional theory (DFT) and two central force embedded atom interaction models (Zope and Mishin 2003 Phys. Rev. B 68 024102, Hammerschmidt et al 2005 Phys. Rev. B 71 205409). The results are compared with previously published calculations, except pair potential calculations, which are not appropriate for the description of the metallic bond. The comparison includes N-body central force (NB-CF) and N-body angular (NB-A) empirical potentials, tight-binding approximation to the electronic structure (TB), DFT pseudopotential (DFT-P) and all electron (DFT-A) calculations. None of the considered interaction models are fully satisfactory for the description of these properties. In particular, NB-CF, NB-A and TB interaction models are unable to describe the softening of the easy prismatic γ-surface leading to the appearance of a metastable stacking fault, as evidenced in all the DFT calculations. Most often, when the basal stacking fault excess energy is underevaluated, this leads to an inversion of the energetic stability between the I2 basal and the prismatic easy stacking faults. Even the DFT-pseudopotential calculations need to be improved regarding the description of the shear elastic constants. The implications of these results on the core structure and gliding properties of the screw dislocation are analyzed. The calculated dissociation lengths into Shockley partials in both the basal and prismatic planes for the different models compare well with the measured ones in the corresponding simulations of the dislocation core structure when available. Finally, the Peierls stress is also evaluated using the Peierls–Nabarro model and compared with the experimentally measured one. read less NOT USED (high confidence) J. Wang and I. Beyerlein, “Atomic structures of symmetric tilt grain boundaries in hexagonal close packed (hcp) crystals,” Modelling and Simulation in Materials Science and Engineering. 2012. link Times cited: 146 Abstract: Using molecular dynamics (MD) simulations, the dislocation s… read moreAbstract: Using molecular dynamics (MD) simulations, the dislocation structures of symmetric tilt grain boundaries (STGBs) in hexagonal close packed (hcp) crystal structures are studied. STGBs over the entire range of possible rotation angles θ from 0° to 90° are found to have an ordered atomic structure. Formation energy calculations reveal four local minimum-energy boundaries that correspond to coherent grain boundaries (GBs). Deviations in tilt from the basal plane (θ = 0°, , prismatic plane (θ = 90°, , or one of these four minimum-energy boundaries, , result in the formation of a tilt wall (edge-type grain boundary dislocations, GBDs) superimposed on the nearest GB structure in θ-space. As θ deviates far from the rotation angle of one and draws closer to that of an adjacent , an abrupt transition in STGB base boundary structure and GBD Burgers vector occurs. For all θ, the sign and spacing of GBDs depend on θ, and their Burgers vector is either one or two times the interplanar spacing of PB. We present a simple model that generalizes the results to other c/a ratios. Subsequent MD simulations show that (1) the model forecasts the STGB structure to first-order and (2) STGBs with two distinct atomic structures can have remarkably different responses when interacting with basal lattice dislocations originating from the adjoining crystals. read less NOT USED (high confidence) B. Li, H. E. Kadiri, and M. Horstemeyer, “Extended zonal dislocations mediating twinning in titanium,” Philosophical Magazine. 2012. link Times cited: 37 Abstract: Using molecular dynamics (MD) simulations, the twinning mech… read moreAbstract: Using molecular dynamics (MD) simulations, the twinning mechanism in titanium (Ti) was studied by analyzing the interfacial structure at the twin boundary (TB). The simulation results reveal interesting twin growth controlled by interfacial dislocations at the TB. The elementary twinning dislocations (bT ) nucleate and glide in pairs but separately and sequentially on two neighboring planes, significantly different from conventional zonal dislocations, which spread over two or more twinning planes with each plane comprising one Burgers vector of an elementary twinning dislocation. The twin growth can be approximately described as These two separate elementary twinning dislocations amount to a net Burgers vector 2bT ≈ 0.16 nm along the twinning vector , with the components in the in-plane direction perpendicular to η 1 canceled out. These results support the classical twinning theory in which a homogeneous shear and local shuffling have to be involved. A mechanism taking into consideration local structure of the twinning plane for such extended zonal dislocations is discussed. read less NOT USED (high confidence) T. Qin and Z. Fan, “Reconstruction of 2D Al3Ti on TiB2 in an aluminium melt,” IOP Conference Series: Materials Science and Engineering. 2012. link Times cited: 6 Abstract: It has been widely considered that Al3Ti is involved in the … read moreAbstract: It has been widely considered that Al3Ti is involved in the aluminium nucleation on TiB2, although the mechanism has not been fully understood. In this paper molecular dynamics has been conducted to investigate this phenomenon at an atomistic scale. It was found that a two-dimensional Al3Ti layer may remain on TiB2 above the aluminium liquidus. In addition, the results showed that this 2D Al3Ti undergoes interface reconstruction by forming a triangular pattern. This triangular pattern consists of different alternative stacking sequences. The transition region between the triangles forms an area of strain concentration. By means of this mechanism, this interfacial Al3Ti layer stabilizes itself by localizing the large misfit strain between TiB2 and Al3Ti This reconstruction is similar to the hdp-fcc interface reconstruction in other systems which has been observed experimentally [1]. read less NOT USED (high confidence) M. Luskin, C. Ortner, and B. V. Koten, “Formulation and optimization of the energy-based blended quasicontinuum method,” arXiv: Numerical Analysis. 2011. link Times cited: 48 NOT USED (high confidence) M. Friák et al., “Methodological challenges in combining quantum-mechanical and continuum approaches for materials science applications,” The European Physical Journal Plus. 2011. link Times cited: 26 NOT USED (high confidence) K. Zhou, H. P. Wang, J. Chang, and B. Wei, “Surface tension of substantially undercooled liquid Ti–Al alloy,” Philosophical Magazine Letters. 2010. link Times cited: 7 Abstract: It is usually difficult to undercool Ti–Al alloys on account… read moreAbstract: It is usually difficult to undercool Ti–Al alloys on account of their high reactivity in the liquid state. This results in a serious scarcity of information on their thermophysical properties in the metastable state. Here, we report on the surface tension of a liquid Ti–Al alloy under high undercooling condition. By using the electromagnetic levitation technique, a maximum undercooling of 324 K (0.19 T L) was achieved for liquid Ti-51 at.% Al alloy. The surface tension of this alloy, which was determined over a broad temperature range 1429–2040 K, increases linearly with the enhancement of undercooling. The experimental value of the surface tension at the liquidus temperature of 1753 K is 1.094 N m−1 and its temperature coefficient is −1.422 × 10−4 N m−1 K−1. The viscosity, solute diffusion coefficient and Marangoni number of this liquid Ti–Al alloy are also derived from the measured surface tension. read less NOT USED (high confidence) C. Ji et al., “Composition dependent phase transformation of Pt0.5−xMn0.5+x from A1 to L10 phase,” Applied Physics A. 2010. link Times cited: 0 NOT USED (high confidence) Y. Mishin, M. Asta, and J. Li, “Atomistic modeling of interfaces and their impact on microstructure and properties,” Acta Materialia. 2010. link Times cited: 418 NOT USED (high confidence) G. P. P. Pun and Y. Mishin, “Development of an interatomic potential for the Ni-Al system,” Philosophical Magazine. 2009. link Times cited: 341 Abstract: We construct an interatomic potential for the Ni-Al system w… read moreAbstract: We construct an interatomic potential for the Ni-Al system within the embedded-atom method formalism. The potential is based on previously developed accurate potentials for pure Ni and Al. The cross-interactions are fitted to experimental cohesive energy, lattice parameter and elastic constants of B2-NiAl, as well as to ab initio formation energies of several real or imaginary intermetallic compounds with different crystal structures and chemical compositions. The potential accurately reproduces a variety of physical properties of the NiAl and Ni3Al phases, and shows reasonable agreement with experimental and ab initio data for phase stability across the Ni-Al phase diagram. Most of the properties reproduced by the new potential were not involved in the fitting process, which demonstrates its excellent transferability. Advantages and certain weaknesses of the new potential in comparison with other existing potentials are discussed in detail. The potential is expected to be especially suitable for simulations of heterophase interfaces and mechanical behavior of Ni-Al alloys. read less NOT USED (high confidence) A. Alam and D. D. Johnson, “Optimal site-centered electronic structure basis set from a displaced-center expansion: Improved results via a priori estimates of saddle points in the density,” Physical Review B. 2009. link Times cited: 17 NOT USED (high confidence) H.-B. Zhou, Y. Zhang, Y.-L. Liu, M. Kohyama, P. Yin, and G. Lu, “First-principles characterization of the anisotropy of theoretical strength and the stress–strain relation for a TiAl intermetallic compound,” Journal of Physics: Condensed Matter. 2009. link Times cited: 29 Abstract: We perform first-principles computational tensile and compre… read moreAbstract: We perform first-principles computational tensile and compressive tests (FPCTT and FPCCT) to investigate the intrinsic bonding and mechanical properties of a γ-TiAl intermetallic compound (L 10 structure) using a first-principles total energy method. We found that the stress–strain relations and the corresponding theoretical tensile strengths exhibit strong anisotropy in the [001], [100] and [110] crystalline directions, originating from the structural anisotropy of γ-TiAl. Thus, γ-TiAl is a representative intermetallic compound that includes three totally different stress–strain modes. We demonstrate that all the structure transitions in the FPCTT and FPCCT result from the breakage or formation of bonds, and this can be generalized to all the structural transitions. Furthermore, based on the calculations we qualitatively show that the Ti–Al bond should be stronger than the Ti–Ti bond in γ-TiAl. Our results provide a useful reference for understanding the intrinsic bonding and mechanical properties of γ-TiAl as a high-temperature structural material. read less NOT USED (high confidence) T. Radchenko and V. Tatarenko, “Fe–Ni Alloys at High Pressures and Temperatures: Statistical Thermodynamics and Kinetics of the L1_2 or D0_19 Atomic Order.” 2008. link Times cited: 19 NOT USED (high confidence) Y. Mishin and A. Lozovoi, “Angular-dependent interatomic potential for tantalum,” Acta Materialia. 2006. link Times cited: 70 NOT USED (high confidence) Y. Mishin, M. Mehl, D. Papaconstantopoulos, and D. Papaconstantopoulos, “Phase stability in the Fe–Ni system: Investigation by first-principles calculations and atomistic simulations,” Acta Materialia. 2005. link Times cited: 261 NOT USED (high confidence) X. J. Han, M. Chen, and Z. Guo, “A Molecular Dynamics Study for the Thermophysical Properties of Liquid Ti–Al Alloys,” International Journal of Thermophysics. 2005. link Times cited: 12 NOT USED (high confidence) R. Benedek, A. Walle, S. Gerstl, M. Asta, D. Seidman, and C. Woodward, “Partitioning of solutes in multiphase Ti-Al alloys,” Physical Review B. 2005. link Times cited: 35 Abstract: First-principles calculations based on a plane-wave pseudopo… read moreAbstract: First-principles calculations based on a plane-wave pseudopotential method, as implemented in the VASP code, are presented for the formation energies of several transition-metal and non-transition-metal dopants in Ti‐ Al alloys. Substitution for either Ti or Al in g-TiAl, a2-Ti3Al, Ti2AlC, and Ti3AlC are considered. Calculated szero-temperatured defect formation energies exhibit clear trends as a function of the periodic-table column of transition metal solutes. Early transition metals in TiAl prefer the Ti sublattice, but this preference gradually shifts to the Al sublattice for late transition metals; the Ti sublattice is preferred by all transition metal solutes in Ti3Al. Partitioning of solutes to Ti 3Al is predicted for mid-period transition elements, and to TiAl for early and late transition elements. A simple Ising model treatment demonstrates the plausibility of these trends, which are in excellent overall agreement with experiment. The influence of temperature on formation energies is examined with a cluster expansion for the binary TiAl alloys and a low temperature expansion for dilute ternary alloys. Results for Nb-doped alloys provide insight into the relative sensitivity of solute partitioning to individual contributions to the free energy. Whereas the calculated formation energy of Nb ssubstitutiond at zero temperature favors partitioning to a2-Ti3Al, temperature-dependent contributions to the formation free energy, evaluated at 1075 K, favor partitioning to g-TiAl, in agreement with experiment. read less NOT USED (high confidence) Q. Pei, C. Lu, and H. P. Lee, “Crystallization of amorphous alloy during isothermal annealing: a molecular dynamics study,” Journal of Physics: Condensed Matter. 2005. link Times cited: 50 Abstract: The crystallization process of a Ti–Al amorphous alloy durin… read moreAbstract: The crystallization process of a Ti–Al amorphous alloy during isothermal annealing was studied with molecular dynamics simulations. The structural development and phase transformation were analysed based on the variations of the internal energy, cell volume, radial distribution function, bond pairs, and atomic configuration. The crystal nucleation, grain growth, and grain coarsening during the crystallization process were studied. The three-stage feature of the crystallization process was identified. The simulation results also show that there are transformations from a metastable crystal phase to a more stable crystal phase during the crystallization. read less NOT USED (high confidence) Q. Pei, C. Lu, and M. Fu, “The rapid solidification of Ti3Al : a molecular dynamics study,” Journal of Physics: Condensed Matter. 2004. link Times cited: 26 Abstract: The rapid solidification of Ti3Al was studied with the const… read moreAbstract: The rapid solidification of Ti3Al was studied with the constant-pressure and constant-temperature molecular dynamics (NPT-MD) technique to obtain an atomistic description of glass formation and crystallization in the alloy. The embedded atom method (EAM) potential for the Ti?Al binary system recently developed by Zope and Mishin (2003?Phys.?Rev.?B?68?024102) was applied in the simulations. The effects of different cooling rates on the glass formation and crystallization of liquid Ti3Al were studied. In addition, the crystallization of the amorphous Ti3Al as a function of increasing temperature was also studied. The calculated internal energy change and radial distribution function during cooling and heating processes provided a good picture of the structural transformations, and the results were consistent with the results obtained experimentally. read less NOT USED (high confidence) S. Koch, “Development of RF-MEAM interaction potentials for Fe-Y.” 2019. link Times cited: 0 Abstract: Der Fokus dieser Arbeit lag zunachst auf einer simulationsge… read moreAbstract: Der Fokus dieser Arbeit lag zunachst auf einer simulationsgestutzen Untersuchung uber die Entsteh- ungsmechanismen von Oxidteilchen in ODS-Stahlen. Hierbei bilden empirische Wechselwirkungs- potenziale von Eisen-Yttrium-Sauerstoff (Fe-Y-O) die Grundlage fur eine Beschreibung dieser Oxid- teilchen-Bildungs-Prozesse in Molekulardynamik (MD) Simulationen, die auch Eigenschaften von Versetzungen und anderen Bestrahlungs-Panomenen detailiert zur weiteren Aufklarung behandeln konnen.
Zu diesem Zweck ist das speziell auf die Simulation zugeschnittene Anfitten der o.g. MD Potenziale (hier fur Fe-Y-O) notwendig. Hierzu dienen die zuvor durchgefuhrten ab-initio (DFT) Rechnungen als Daten- referenzgrundlage (z.B. von Phasen oder Defekten) zur Optimierung der Potenzialparameter wahrend des Anfittens, um ein moglichst exaktes MD Potenzial zu erzeugen, dass die ab-initio Daten auf groseren MD Skalen detailgetreu abbildet. Im ersten Drittel dieses Projektes wurden mehrere Potenziale fur die einzelnen Metall-Komponenten, Fe-Fe und Y-Y, erzeugt. Dabei stellte sich heraus, dass etablierte Standardmethoden nicht in der Lage sind genaue Fe-Y Potenziale als Teillosung fur das Fe-Y-O Problem zu erzeugen. Dabei wurde eine Kombination aus dem (M)EAM Modell und zur Optimierung eine LSM gestutzte Software (POTFIT) genutzt. Die Komplexitat des Problems liegt in den richtungsabhangigen Atombindungen, die die hier entwickelten fortgeschrittenen Simulations- und Fitmethoden benotigen.
Im ersten Schritt von drei Schritten (chapter 3) wurden zunachst einmal die Defizite der Standard-Fittechniken evaluiert, indem die wahrend des Fitting-Prozesses gefundenen Parametersets im EAM Formalismus mit der flexiblen Software POTFIT auf ihre Eignung hin grundlich untersucht worden sind. Die hierfur genutzten Fitfunktionen wurden ursprunglich Anfang 2000 von Zhou und Wadley entwickelt. Hierbei liegt die Ursache fur die dann entdeckte Parameterset-Problematik darin, dass zur Beschreibung des Fe-Y Systems das Model aus drei Potentialkomponenten besteht: Fe-Fe, Y-Y und Fe-Y. Fur diese einzelnen Komponenten sind die Potentialparameter erfolgreich angefittet worden mit Bezug zur Gitterkonstante und Bindungs- bzw. Kohasionsenergie (beides mit 1% Genauigkeit bezgl. DFT Rechnungen) sowie zu allen elastischen Konstanten (5% Genauigkeit bezgl. Experimente). All dies unter Zuhilfenahme von Parametersuchraum-beschrankenden Techniken, die zur Einhaltung der oben genannten Eigenschaften dienen und urspurnglich von Johnson & Oh sind. Selbst kompliziertere Defekteigenschaften, wie Zwischengitter- und Leerstellenbildungsenergien wurden erfolgreich angefittet. Das hier entwickelte EAM Potenzial fur Y-Y ist z.B. in der Lage bei Eigenzwischengitteratomen die basal oktaedrische Position von Zwischengitteratomen (ZA) im Yttrium hcp-Gitter als Grundzustand und die Transition eines jeden ZAs aus einer anderen Position, wie zuvor in DFT berechnet, zu reproduzieren.
Zur Bildung des angestrebten Fe-Y Potenzials wurden diese beiden Komponenten, Fe-Fe und Y-Y, zum weiteren Fitten in dem weitgefacherten und komplexen Fe-Y Potzenzialsuchraum genutzt. Die Parametersets wurden mit sogenannten hier entwickelten Hauptparameter (Key Driver) systematisch untersucht. Ein flexibleres Konzept statt der starreren Universal Binding Relations in Abhangigkeit von der Rose Gleichung. Dieser Hauptparameter zeigte eindeutig, dass die Nutzung der Rose Gleichung zur Parametersuchraum-Minimierung den Suchraum dahingehend einschrankt, sodass ein akkurates Anfitten der hier genutzten 900 DFT Datensets nicht mehr moglich ist. Allerdings ist die Orientierung im Parametersuchraum mit dieser Rose Gleichung bei standardmasigen Optimierungsmethoden (wie LSM) unabdingbar, da ohne diese die benotigten globalen Optima fur die Parameter nicht auffindbar sind.
Als aufklarendes Testverfahren zur weiteren Ergrundung dieser Problematik und Prufung zur Eignung fur Fe-Y Potenziale und den anschliesenden Simulationen diente der Versuch, 9 verschiedene Bindungs-energien von Yttrium-Leerstellenclustern mit ansteigender Leerstellenzahl zu reproduzieren. Dieser Test konnte von diesen Potenzialen nur teilweise erfullt werden und wurde auf die fehlende Beschreibung der Bindungswinkelabhangigkeit im Modell zuruckgefuhrt. Die Erweiterung von EAM durch MEAM mit Winkelabhangigkeit ist jedoch keineswegs eine zufriedenstellende Losung, da MEAM alternativlos auf der irrefuhrenden Rose Gleichung beruht. Daher war die Benutzung des ubersichtlicheren EAM Typs aus zwei Grunden nutzlich: 1. MEAM braucht die Rose Gleichung um diesen komplexen Formalismus zu beherrschen mit denselben Problemen wie in EAM, aber dieses grundlegende Problem ist in MEAM deutlich schwerer zu identifizieren als in EAM. 2. Die mit EAM gefundenen, angefitteten Parameter sind eine hervorragende Startparameter-Grundlage fur den verbesserten darauffolgenden RF-MEAM Typ.
Im zweiten Schritt wurde das Problem aus dem ersten Schritt gelost, indem ein modifizierter MEAM Spezialtyp im referenzlosen Format (RF-MEAM) angewandt worden ist. Im Gegensatz zum herkommlichen MEAM wird hier die Rose Gleichung durch mehr DFT Daten und insbesondere einer intelligenteren Machine Learning ahnlichen Genetic Algorithmus (GA) Optimiertechnik ersetzt, die allerdings eine bedachte Startparameterwahl vorraussetzt, womit Schritt 1 wieder ins Spiel kommt. Die genutzte fortgeschrittene MEAMfit Software, die per GA funktioniert, wurde zwischen 2016 und 2017 funktionierend eigens dafur implementiert. Mit den in Schritt 1 gefitteten Parametern und Set-Auswahltechniken konnten die weiterfuhrenden Fits mit optimalen Startparametern durchgefuhrt werden.
Auf dieser Stufe waren diese Fits mit der speziell verbesserten Technik in der Lage ein detailgetreues Fe-Y Potenzial zu generieren, das sowohl alle Phasen (Fe2Y, Fe3Y, Fe5Y, Fe23Y6 und Fe17Y2 sowohl als auch reines Fe und Y) als auch die gesamte Defektdatenbasis mit einer durchschnittlichen Abweichung von ≈11% erfolgreich abbildet. Zusatzlich bestatigend zu dieser allgemeinen Ubereinstimmung wurde konsequenterweise der in Schritt 1 entwickelte Test hervorragend mit einmaliger Genauigkeit bestanden, mit max. 5% Abweichung von den komlexen o.g. Y-Leerstellen Bildungsenergien. Allerdings konnte ein systematischer Fehlertrend aufgespurt werden, der Schwachen in der Fe-Fe Komponente offenbarte. Als Folge dessen wurde umgehend diese Komponente durch ein anderes etabliertes Fe-Fe Potenzial von G. Ackland mit einer extrem genauen Schmelztemperatur (nur 3% Abweichung vom Exp.) ausgetauscht. Mit diesem genauen Potenzial konnte zum ersten Mal die Clusterbildung von gelosten Yttrium Atomen in einer Eisenschmelze erfolgreich per MD Simulation auf atomarer Ebene nachgestellt werden oberhalb von 1750 K. Temperaturen darunter hatten eine Ausscheidungsbildung von Y mit sehr geringer Y-Loslichkeit (<0.1%) in Ubereinstimmung mit den Experimenten zur Folge. Dies wurde durch den Pot. Typ A ermoglicht, der aber die energetische Reihenfolge bei den Fe-Y Phasen nicht ganz genau einhalt. Typ B hingegen halt diese ein, dort fehlt aber die Y-Clusterbildungsneigung. Durch den gebotenen Praxisbezug zur Metallurgie mussen die Loslichkeit und Clusterbildung gleichzeitig in der Simulation genau reproduzierbar sein, was aber weder Typ A noch B kann, was zum Typ A/B Dilemma fuhrt.
Dieses Typ A/B Dilemma (Phasen oder Defekt Genauigkeit) fuhrt zum letzten dritten Schritt (chapter 5). Darin ist zusatzlich die Strukturaufklarung von der Fe17Y2 Phase mit Vergleichen zu exp. EXAFS Spektren unserer Kollaborationspartner vom ISSP (Riga) enthalten. Diese Aufklarung dient auch dazu die fehlenden magnetischen Abhangigkeiten im Potenzial zu kompensieren, da die Phasenreihenfolge mit sehr feinen Energieunterschieden wohl stark von magnetischen Wechselwirkungen gepragt ist. Obwohl Potenzial Typ B diesen (Magnetismus) nicht direkt beachtet, ist es in der Lage das tatsachlich gemessene EXAFS Spektrum grostenteils genau wiederzugeben. Allerdings offenbart eine einzige ausgepragte Phasenverschiebung, dass die angenommene hcp Struktur durch eine unterschwellige rhombohedrale Komponente, die sporadisch in der c-Gitterrichtung auftritt, korrigiert werden muss. AIMD (DFT) Berechnungen in Kooperation mit der University of Edinburgh bestatigen dies und zeigen sogar, dass magnetische Wechselwirkungen diese Strukturmischung stabilisieren. Endgultig bestatigt werden konnte dies mit der genauen EXAFS Spektren Reproduktion mit dem durch AIMD verbesserten nochmals gefitteten Potenzialtyp B, der als neuer Typ C durch AIMD indirekt den Einfluss der magnetischen Wechselwirkungen mit einschliest. Diese erstmalige nahezu deckungsgleiche MD Simulation eines EXAFS Spektrums von einem komplexen metallischen Alloy, hier Fe-Y, stellt eine bisher unerreichte Verbesserung dar. Schlieslich lost Typ C das Typ A/B Dilemma und ernoglicht eine genaue gleichzeitige MD Modellierung von Phasen- und Defekten in Fe-Y – ein Durchbruch in der MD-Potenzialentwicklung. read less NOT USED (high confidence) Y.-hua Zhou, A. L. Lloyd, R. Smith, and S. Kenny, “Modelling thin film growth in the Ag–Ti system,” Surface Science. 2019. link Times cited: 2 NOT USED (high confidence) S. Rawat and N. Mitra, “Molecular dynamics investigation of c-axis deformation of single crystal Ti under uniaxial stress conditions: Evolution of compression twinning and dislocations,” Computational Materials Science. 2018. link Times cited: 28 NOT USED (high confidence) S. Rawat and N. Mitra, “Compression twinning and structural phase transformation of single crystal titanium under uniaxial compressive strain conditions: Comparison of inter-atomic potentials,” Computational Materials Science. 2017. link Times cited: 29 NOT USED (high confidence) J. S. Gibson, S. G. Srinivasan, M. Baskes, R. E. Miller, and A. K. Wilson, “A multi-state modified embedded atom method potential for titanium,” Modelling and Simulation in Materials Science and Engineering. 2016. link Times cited: 3 Abstract: The continuing search for broadly applicable, predictive, an… read moreAbstract: The continuing search for broadly applicable, predictive, and unique potential functions led to the invention of the multi-state modified embedded atom method (MS-MEAM) (Baskes et al 2007 Phys. Rev. B 75 094113). MS-MEAM replaced almost all of the prior arbitrary choices of the MEAM electron densities, embedding energy, pair potential, and angular screening functions by using first-principles computations of energy/volume relationships for multiple reference crystal structures and transformation paths connecting those reference structures. This strategy reasonably captured diverse interactions between atoms with variable coordinations in a face-centered-cubic (fcc)-stable copper system. However, a straightforward application of the original MS-MEAM framework to model technologically useful hexagonal-close-packed (hcp) metals proved elusive. This work describes the development of an hcp-stable/fcc-metastable MS-MEAM to model titanium by introducing a new angular function within the background electron density description. This critical insight enables the titanium MS-MEAM potential to reproduce first principles computations of reference structures and transformation paths extremely well. Importantly, it predicts lattice and elastic constants, defect energetics, and dynamics of non-ideal hcp and liquid titanium in good agreement with first principles computations and corresponding experiments, and often better than the three well-known literature models used as a benchmark. The titanium MS-MEAM has been made available in the Knowledgebase of Interatomic Models (https://openkim.org/) (Tadmor et al 2011 JOM 63 17). read less NOT USED (high confidence) T. Luther, “Adaptation of atomistic and continuum methods for multiscale simulation of quasi-brittle intergranular damage.” 2010. link Times cited: 0 Abstract: The numerical simulation of damage using phenomenological mo… read moreAbstract: The numerical simulation of damage using phenomenological models on the macroscale was state of the art for many decades. However, such models are not able to capture the complex nature of damage, which simultaneously proceeds on multiple length scales. Furthermore, these phenomenological models usually contain damage parameters, which are physically not interpretable. Consequently, a reasonable experimental determination of these parameters is often impossible. In the last twenty years, the ongoing advance in computational capacities provided new opportunities for more and more detailed studies of the microstructural damage behavior. Today, multiphase models with several million degrees of freedom enable for the numerical simulation of micro-damage phenomena in naturally heterogeneous materials. Therewith, the application of multiscale concepts for the numerical investigation of the complex nature of damage can be realized. The presented thesis contributes to a hierarchical multiscale strategy for the simulation of brittle intergranular damage in polycrystalline materials, for example aluminum. The numerical investigation of physical damage phenomena on an atomistic microscale and the integration of these physically based information into damage models on the continuum meso- and macroscale is intended. Therefore, numerical methods for the damage analysis on the micro- and mesoscale including the scale transfer are presented and the transition to the macroscale is discussed. The investigation of brittle intergranular damage on the microscale is realized by the application of the nonlocal Quasicontinuum method, which fully describes the material behavior by atomistic potential functions, but reduces the number of atomic degrees of freedom by introducing kinematic couplings. Since this promising method is applied only by a limited group of researchers for special problems, necessary improvements have been realized in an own parallelized implementation of the 3D nonlocal Quasicontinuum method. The aim of this implementation was to develop and combine robust and efficient algorithms for a general use of the Quasicontinuum method, and therewith to allow for the atomistic damage analysis in arbitrary grain boundary configurations. The implementation is applied in analyses of brittle intergranular damage in ideal and nonideal grain boundary models of FCC aluminum, considering arbitrary misorientations. From the microscale simulations traction separation laws are derived, which describe grain boundary decohesion on the mesoscale. Traction separation laws are part of cohesive zone models to simulate the brittle interface decohesion in heterogeneous polycrystal structures. 2D and 3D mesoscale models are presented, which are able to reproduce crack initiation and propagation along cohesive interfaces in polycrystals. An improved Voronoi algorithm is developed in 2D to generate polycrystal material structures based on arbitrary distribution functions of grain size. The new model is more flexible in representing realistic grain size distributions. Further improvements of the 2D model are realized by the implementation and application of an orthotropic material model with Hill plasticity criterion to grains. The 2D and 3D polycrystal models are applied to analyze crack initiation and propagation in statically loaded samples of aluminum on the mesoscale without the necessity of initial damage definition. read less NOT USED (high confidence) H.-B. Zhou, Y. Wei, Y.-L. Liu, Y. Zhang, and G. Lu, “First-principles investigation of site preference and bonding properties of alloying element in TiAl with O impurity,” Modelling and Simulation in Materials Science and Engineering. 2009. link Times cited: 14 Abstract: We have investigated site preference and bonding properties … read moreAbstract: We have investigated site preference and bonding properties of alloying elements including Nb, Mo, Ni and Ag in TiAl with O impurity using a first-principles method based on the density functional theory. We found that the preferable sites for O are the Ti-rich octahedral interstitial ones, while those for the alloying elements are the substitutional ones. Among these elements which are beneficial to improve the mechanical properties of TiAl, Ni and Ag occupy the Al sites, while Nb and Mo occupy the Ti sites. We demonstrate that the presence of O alters the site preference of these alloying elements in TiAl, making these elements prefer to substitute Al that is the first nearest neighbor of O, because O prefers to bond with Ti rather than Al. We suggest that, according to the local density of states results, O can be deleterious to the ductility of TiAl with Nb and Mo, but has little effect on that of TiAl with Ni and Ag. read less |
 EAM_Dynamo_ZopeMishin_2003_TiAl__MO_117656786760_005
EAM_Dynamo_ZopeMishin_2003_TiAl__MO_117656786760_005