EMT_Asap_Standard_JacobsenStoltzeNorskov_1996_Pt__MO_637493005914_001
| Title
A single sentence description.
|
EMT potential for Pt developed by Jacobsen, Stoltze, and Norskov (1996) v001 |
|---|---|
| Description
A short description of the Model describing its key features including for example: type of model (pair potential, 3-body potential, EAM, etc.), modeled species (Ac, Ag, ..., Zr), intended purpose, origin, and so on.
|
Effective Medium Theory (EMT) model based on the EMT implementation in ASAP (https://wiki.fysik.dtu.dk/asap). Effective Medium Theory is a many-body potential of the same class as Embedded Atom Method, Finnis-Sinclair etc. The main term in the energy per atom is the local density of atoms. The functional form implemented here is that of Ref. 1. The principles behind EMT are described in Refs. 2 and 3 (with 2 being the more detailed and 3 being the most pedagogical). Be aware that the functional form and even some of the principles have changed since refs 2 and 3. EMT can be considered the last step of a series of approximations starting with Density Functional Theory; see Ref 4. This model implements the "official" parametrization as published in Ref. 1. This parametrization is appropriate for single-element simulations of platinum (Pt). For alloy simulations, please use the alloy parametrization EMT_Asap_Standard_JacobsenStoltzeNorskov_1996_AlAgAuCuNiPdPt which uses a slightly larger cutoff to accomodate for all the elements, at the price of changing the properties of the individual elements marginally. These files are based on Asap version 3.11.5. REFERENCES: [1] Jacobsen, K. W., Stoltze, P., & Nørskov, J.: "A semi-empirical effective medium theory for metals and alloys". Surf. Sci. 366, 394–402 (1996). [2] Jacobsen, K. W., Nørskov, J., & Puska, M.: "Interatomic interactions in the effective-medium theory". Phys. Rev. B 35, 7423–7442 (1987). [3] Jacobsen, K. W.: "Bonding in Metallic Systems: An Effective-Medium Approach". Comments Cond. Mat. Phys. 14, 129-161 (1988). [4] Chetty, N., Stokbro, K., Jacobsen, K. W., & Nørskov, J.: "Ab initio potential for solids". Phys. Rev. B 46, 3798–3809 (1992). KNOWN ISSUES / BUGS: * On-the-fly modifications of the parameters is not supported, and should be implemented in the future. |
| Species
The supported atomic species.
| Pt |
| Disclaimer
A statement of applicability provided by the contributor, informing users of the intended use of this KIM Item.
|
None |
| Content Origin | https://gitlab.com/asap/asap |
| Contributor |
Jakob Schiøtz |
| Maintainer |
Jakob Schiøtz |
| Developer |
Jens K. Nørskov Karsten W. Jacobsen P. Stoltze |
| Published on KIM | 2019 |
| How to Cite |
This Model originally published in [1] is archived in OpenKIM [2-5]. [1] Jacobsen KW, Stoltze P, Nørskov JK. A semi-empirical effective medium theory for metals and alloys. Surface Science. 1996;366(2):394–402. doi:10.1016/0039-6028(96)00816-3 — (Primary Source) A primary source is a reference directly related to the item documenting its development, as opposed to other sources that are provided as background information. [2] Nørskov JK, Jacobsen KW, Stoltze P. EMT potential for Pt developed by Jacobsen, Stoltze, and Norskov (1996) v001. OpenKIM; 2019. doi:10.25950/e28557e7 [3] Jacobsen KW, Stoltze P, Nørskov JK. Effective Medium Theory (EMT) potential driver v004. OpenKIM; 2019. doi:10.25950/7e5b8be7 [4] Tadmor EB, Elliott RS, Sethna JP, Miller RE, Becker CA. The potential of atomistic simulations and the Knowledgebase of Interatomic Models. JOM. 2011;63(7):17. doi:10.1007/s11837-011-0102-6 [5] Elliott RS, Tadmor EB. Knowledgebase of Interatomic Models (KIM) Application Programming Interface (API). OpenKIM; 2011. doi:10.25950/ff8f563a |
| Citations
This panel presents information regarding the papers that have cited the interatomic potential (IP) whose page you are on. The OpenKIM machine learning based Deep Citation framework is used to determine whether the citing article actually used the IP in computations (denoted by "USED") or only provides it as a background citation (denoted by "NOT USED"). For more details on Deep Citation and how to work with this panel, click the documentation link at the top of the panel. 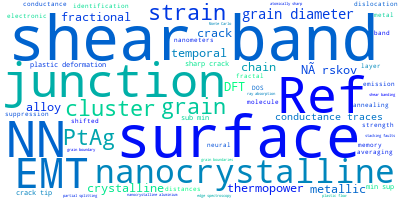The word cloud to the right is generated from the abstracts of IP principle source(s) (given below in "How to Cite") and the citing articles that were determined to have used the IP in order to provide users with a quick sense of the types of physical phenomena to which this IP is applied. 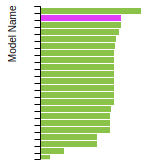The bar chart shows the number of articles that cited the IP per year. Each bar is divided into green (articles that USED the IP) and blue (articles that did NOT USE the IP). Users are encouraged to correct Deep Citation errors in determination by clicking the speech icon next to a citing article and providing updated information. This will be integrated into the next Deep Citation learning cycle, which occurs on a regular basis. OpenKIM acknowledges the support of the Allen Institute for AI through the Semantic Scholar project for providing citation information and full text of articles when available, which are used to train the Deep Citation ML algorithm. |
This panel provides information on past usage of this interatomic potential (IP) powered by the OpenKIM Deep Citation framework. The word cloud indicates typical applications of the potential. The bar chart shows citations per year of this IP (bars are divided into articles that used the IP (green) and those that did not (blue)). The complete list of articles that cited this IP is provided below along with the Deep Citation determination on usage. See the Deep Citation documentation for more information. 
Help us to determine which of the papers that cite this potential actually used it to perform calculations. If you know, click the .
|
| Funding | Not available |
| Short KIM ID
The unique KIM identifier code.
| MO_637493005914_001 |
| Extended KIM ID
The long form of the KIM ID including a human readable prefix (100 characters max), two underscores, and the Short KIM ID. Extended KIM IDs can only contain alpha-numeric characters (letters and digits) and underscores and must begin with a letter.
| EMT_Asap_Standard_JacobsenStoltzeNorskov_1996_Pt__MO_637493005914_001 |
| DOI |
10.25950/e28557e7 https://doi.org/10.25950/e28557e7 https://commons.datacite.org/doi.org/10.25950/e28557e7 |
| KIM Item Type
Specifies whether this is a Portable Model (software implementation of an interatomic model); Portable Model with parameter file (parameter file to be read in by a Model Driver); Model Driver (software implementation of an interatomic model that reads in parameters).
| Portable Model using Model Driver EMT_Asap__MD_128315414717_004 |
| Driver | EMT_Asap__MD_128315414717_004 |
| KIM API Version | 2.0.2 |
| Potential Type | eam |
| Previous Version | EMT_Asap_Standard_JacobsenStoltzeNorskov_1996_Pt__MO_637493005914_000 |
| Grade | Name | Category | Brief Description | Full Results | Aux File(s) |
|---|---|---|---|---|---|
| P | vc-species-supported-as-stated | mandatory | The model supports all species it claims to support; see full description. |
Results | Files |
| P | vc-periodicity-support | mandatory | Periodic boundary conditions are handled correctly; see full description. |
Results | Files |
| P | vc-permutation-symmetry | mandatory | Total energy and forces are unchanged when swapping atoms of the same species; see full description. |
Results | Files |
| A | vc-forces-numerical-derivative | consistency | Forces computed by the model agree with numerical derivatives of the energy; see full description. |
Results | Files |
| F | vc-dimer-continuity-c1 | informational | The energy versus separation relation of a pair of atoms is C1 continuous (i.e. the function and its first derivative are continuous); see full description. |
Results | Files |
| P | vc-objectivity | informational | Total energy is unchanged and forces transform correctly under rigid-body translation and rotation; see full description. |
Results | Files |
| P | vc-inversion-symmetry | informational | Total energy is unchanged and forces change sign when inverting a configuration through the origin; see full description. |
Results | Files |
| P | vc-memory-leak | informational | The model code does not have memory leaks (i.e. it releases all allocated memory at the end); see full description. |
Results | Files |
| P | vc-thread-safe | mandatory | The model returns the same energy and forces when computed in serial and when using parallel threads for a set of configurations. Note that this is not a guarantee of thread safety; see full description. |
Results | Files |
| P | vc-unit-conversion | mandatory | The model is able to correctly convert its energy and/or forces to different unit sets; see full description. |
Results | Files |
| N/A | vc-contributing-atom-energy | informational | other |
Results | Files |
BCC Lattice Constant
This bar chart plot shows the mono-atomic body-centered cubic (bcc) lattice constant predicted by the current model (shown in the unique color) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
Cohesive Energy Graph
This graph shows the cohesive energy versus volume-per-atom for the current mode for four mono-atomic cubic phases (body-centered cubic (bcc), face-centered cubic (fcc), simple cubic (sc), and diamond). The curve with the lowest minimum is the ground state of the crystal if stable. (The crystal structure is enforced in these calculations, so the phase may not be stable.) Graphs are generated for each species supported by the model.
Diamond Lattice Constant
This bar chart plot shows the mono-atomic face-centered diamond lattice constant predicted by the current model (shown in the unique color) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
Dislocation Core Energies
This graph shows the dislocation core energy of a cubic crystal at zero temperature and pressure for a specific set of dislocation core cutoff radii. After obtaining the total energy of the system from conjugate gradient minimizations, non-singular, isotropic and anisotropic elasticity are applied to obtain the dislocation core energy for each of these supercells with different dipole distances. Graphs are generated for each species supported by the model.
FCC Elastic Constants
This bar chart plot shows the mono-atomic face-centered cubic (fcc) elastic constants predicted by the current model (shown in blue) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
FCC Lattice Constant
This bar chart plot shows the mono-atomic face-centered cubic (fcc) lattice constant predicted by the current model (shown in red) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
FCC Stacking Fault Energies
This bar chart plot shows the intrinsic and extrinsic stacking fault energies as well as the unstable stacking and unstable twinning energies for face-centered cubic (fcc) predicted by the current model (shown in blue) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
FCC Surface Energies
This bar chart plot shows the mono-atomic face-centered cubic (fcc) relaxed surface energies predicted by the current model (shown in blue) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
SC Lattice Constant
This bar chart plot shows the mono-atomic simple cubic (sc) lattice constant predicted by the current model (shown in the unique color) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
Cubic Crystal Basic Properties Table
Species: PtThis Model requires a Model Driver. Click below for the Model Driver EMT_Asap__MD_128315414717_004 archive.