Sim_LAMMPS_ReaxFF_AnGoddard_2015_BC__SM_389039364091_000
| Title
A single sentence description.
|
LAMMPS ReaxFF potential for B4C developed by An and Goddard (2015) v000 |
|---|---|
| Description | ReaxFF potential for shock/non-equilibrium studies of boron carbide |
| Species
The supported atomic species.
| B, C |
| Disclaimer
A statement of applicability provided by the contributor, informing users of the intended use of this KIM Item.
|
None |
| Content Origin | “Atomistic Origin of Brittle Failure of Boron Carbide from Large-Scale Reactive Dynamics Simulations: Suggestions toward Improved Ductility”
DOI: 10.1103/PhysRevLett.115.105501 |
| Contributor |
Kimia Ghaffari |
| Maintainer |
Kimia Ghaffari |
| Developer |
An, Q. William A. Goddard |
| Published on KIM | 2023 |
| How to Cite |
This Simulator Model originally published in [1] is archived in OpenKIM [2-4]. [1] An Q, Goddard WA. Atomistic Origin of Brittle Failure of Boron Carbide from Large-Scale Reactive Dynamics Simulations: Suggestions toward Improved Ductility. Phys Rev Lett [Internet]. 2015Aug;115(10):105501. Available from: https://link.aps.org/doi/10.1103/PhysRevLett.115.105501 doi:10.1103/PhysRevLett.115.105501 — (Primary Source) A primary source is a reference directly related to the item documenting its development, as opposed to other sources that are provided as background information. [2] An Q, Goddard WA. LAMMPS ReaxFF potential for B4C developed by An and Goddard (2015) v000. OpenKIM; 2023. doi:10.25950/d253fc36 [3] Tadmor EB, Elliott RS, Sethna JP, Miller RE, Becker CA. The potential of atomistic simulations and the Knowledgebase of Interatomic Models. JOM. 2011;63(7):17. doi:10.1007/s11837-011-0102-6 [4] Elliott RS, Tadmor EB. Knowledgebase of Interatomic Models (KIM) Application Programming Interface (API). OpenKIM; 2011. doi:10.25950/ff8f563a Click here to download the above citation in BibTeX format. |
| Citations
This panel presents information regarding the papers that have cited the interatomic potential (IP) whose page you are on. The OpenKIM machine learning based Deep Citation framework is used to determine whether the citing article actually used the IP in computations (denoted by "USED") or only provides it as a background citation (denoted by "NOT USED"). For more details on Deep Citation and how to work with this panel, click the documentation link at the top of the panel. The word cloud to the right is generated from the abstracts of IP principle source(s) (given below in "How to Cite") and the citing articles that were determined to have used the IP in order to provide users with a quick sense of the types of physical phenomena to which this IP is applied. The bar chart shows the number of articles that cited the IP per year. Each bar is divided into green (articles that USED the IP) and blue (articles that did NOT USE the IP). Users are encouraged to correct Deep Citation errors in determination by clicking the speech icon next to a citing article and providing updated information. This will be integrated into the next Deep Citation learning cycle, which occurs on a regular basis. OpenKIM acknowledges the support of the Allen Institute for AI through the Semantic Scholar project for providing citation information and full text of articles when available, which are used to train the Deep Citation ML algorithm. |
This panel provides information on past usage of this interatomic potential (IP) powered by the OpenKIM Deep Citation framework. The word cloud indicates typical applications of the potential. The bar chart shows citations per year of this IP (bars are divided into articles that used the IP (green) and those that did not (blue)). The complete list of articles that cited this IP is provided below along with the Deep Citation determination on usage. See the Deep Citation documentation for more information. 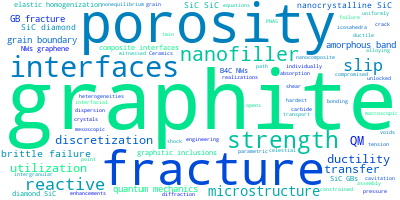
103 Citations (91 used)
Help us to determine which of the papers that cite this potential actually used it to perform calculations. If you know, click the .
USED (high confidence) K. Ramesh et al., “Models for the behavior of boron carbide in extreme dynamic environments,” Journal of the American Ceramic Society. 2021. link Times cited: 9 USED (high confidence) Y. Shen, M. Yang, W. Goddard, and Q. An, “Strengthening boron carbide by doping Si into grain boundaries,” Journal of the American Ceramic Society. 2021. link Times cited: 1 USED (high confidence) J. Clayton, M. Guziewski, J. Ligda, R. B. Leavy, and J. Knap, “A Multi-Scale Approach for Phase Field Modeling of Ultra-Hard Ceramic Composites,” Materials. 2021. link Times cited: 7 Abstract: Diamond-silicon carbide (SiC) polycrystalline composite blen… read more USED (high confidence) N. Song, Z. Gao, and X. Li, “Tailoring nanocomposite interfaces with graphene to achieve high strength and toughness,” Science Advances. 2020. link Times cited: 33 Abstract: Tailoring the composite interfaces with graphene enabled eff… read more USED (high confidence) T. Cheng, A. Jaramillo-Botero, Q. An, D. Ilyin, S. Naserifar, and W. Goddard, “First principles-based multiscale atomistic methods for input into first principles nonequilibrium transport across interfaces,” Proceedings of the National Academy of Sciences. 2018. link Times cited: 7 Abstract: This issue of PNAS features “nonequilibrium transport and mi… read more USED (low confidence) X. Song, C. Liu, Q. Li, Y. Ma, and C. Chen, “Intrinsic dense twinning via release of native strain,” Acta Materialia. 2023. link Times cited: 2 USED (low confidence) J. Y. Li, K. Luo, and Q. An, “Mobile dislocation mediated Hall-Petch and inverse Hall-Petch behaviors in nanocrystalline Al-doped boron carbide,” Journal of the European Ceramic Society. 2023. link Times cited: 0 USED (low confidence) X. Hu et al., “Amorphous shear bands in crystalline materials as drivers of plasticity,” Nature Materials. 2023. link Times cited: 5 USED (low confidence) Y. Chen et al., “Cross-interface growth mechanism of nanotwins in extremely high stacking-fault energy ceramic layer,” Acta Materialia. 2023. link Times cited: 0 USED (low confidence) N. Wang et al., “An Atomistic Study of Plastic Deformation of Smco5 by Amorphous Shear Bands,” SSRN Electronic Journal. 2023. link Times cited: 0 USED (low confidence) J. Y. Li and Q. An, “Nanotwinning-induced pseudoplastic deformation in boron carbide under low temperature,” International Journal of Mechanical Sciences. 2023. link Times cited: 3 USED (low confidence) B. Amirian, B. Abali, and J. Hogan, “The study of diffuse interface propagation of dynamic failure in advanced ceramics using the phase-field approach,” Computer Methods in Applied Mechanics and Engineering. 2023. link Times cited: 1 USED (low confidence) J. Clayton, J. Knap, and R. B. Leavy, “On rate dependence and anisotropy in phase field modeling of polycrystalline fracture,” Mechanics of Materials. 2023. link Times cited: 2 USED (low confidence) J. Clayton, “Modeling Deformation and Fracture of Boron-Based Ceramics with Nonuniform Grain and Phase Boundaries and Thermal-Residual Stress,” Solids. 2022. link Times cited: 2 Abstract: A phase field framework of elasticity, inelasticity, and fra… read more USED (low confidence) X. Li, X. Yang, H. Mei, L. Liu, S. Xu, and J. Zhang, “Boron carbide nanopillars under impact loading: Mechanical response and amorphous bands formation mechanism,” Computational Materials Science. 2022. link Times cited: 0 USED (low confidence) J. Li and Q. An, “Quasiplastic Deformation in Shocked Nanocrystalline Boron Carbide: Grain Boundary Sliding and Local Amorphization,” Journal of the European Ceramic Society. 2022. link Times cited: 7 USED (low confidence) J. Clayton, R. B. Leavy, and J. Knap, “Phase field mechanics of residually stressed ceramic composites,” Philosophical Magazine. 2022. link Times cited: 3 Abstract: ABSTRACT A phase field theory for crystalline solids account… read more USED (low confidence) K. Tan et al., “Impacts of defect distribution on the ignition of crystalline explosives: An insight from the overlapping effect,” Energetic Materials Frontiers. 2022. link Times cited: 2 USED (low confidence) B. Amirian, H. Jafarzadeh, B. Abali, A. Reali, and J. Hogan, “Thermodynamically-consistent derivation and computation of twinning and fracture in brittle materials by means of phase-field approaches in the finite element method,” International Journal of Solids and Structures. 2022. link Times cited: 7 USED (low confidence) H. C. Cekil and M. Özdemir, “The behaviour of Boron Carbide under shock compression conditions: MD simulation results,” Computational Materials Science. 2022. link Times cited: 3 USED (low confidence) J. Clayton, “Nonlinear thermodynamic phase field theory with application to fracture and dynamic inelastic phenomena in ceramic polycrystals,” Journal of the Mechanics and Physics of Solids. 2021. link Times cited: 13 USED (low confidence) C.-J. Wang, K. Luo, J. Wang, and J. Lu, “Carbide-facilitated nanocrystallization of martensitic laths and carbide deformation in AISI 420 stainless steel during laser shock peening,” International Journal of Plasticity. 2021. link Times cited: 59 USED (low confidence) X. Li, L. Liu, H. Mei, S. Xu, J. Li, and J. Zhang, “The formation mechanisms of amorphous bands of boron carbide nanopillars under uniaxial compressions and their effects on mechanical properties from molecular dynamics simulation,” Computational Materials Science. 2021. link Times cited: 1 USED (low confidence) J. Li, Q. An, and L. Liu, “Local amorphization in boron carbide at finite temperature: Strategies toward improved ductility,” Physical Review B. 2021. link Times cited: 6 Abstract: Boron carbide (${\mathrm{B}}_{4}\mathrm{C}$) is superhard, b… read more USED (low confidence) X. Ren, X. Yan, L. Wang, Y. Zhao, and S. Wang, “Strengthening Superhard Materials by Nanostructure Engineering,” Journal of Superhard Materials. 2021. link Times cited: 0 USED (low confidence) A. Zare et al., “Mechanical characterization of boron carbide single crystals,” Journal of the American Ceramic Society. 2021. link Times cited: 5 USED (low confidence) K. Xie et al., “Experimental observations of amorphization in multiple generations of boron carbide,” Journal of the American Ceramic Society. 2021. link Times cited: 5 USED (low confidence) S. Z. Chavoshi, P. S. Branicio, and Q. An, “Transition between Hall-Petch and inverse Hall-Petch behavior in nanocrystalline silicon carbide,” Physical Review Materials. 2021. link Times cited: 9 Abstract: Despite much experimental and simulation effort, the existen… read more USED (low confidence) J. Li, S. Xu, J. Zhang, and L. Liu, “First-Principles Predicting Improved Ductility of Boron Carbide through Element Doping,” Journal of Physical Chemistry C. 2021. link Times cited: 12 USED (low confidence) Y. Shen, J. Fuller, and Q. An, “Mitigating the formation of amorphous shear band in boron carbide,” Journal of Applied Physics. 2021. link Times cited: 5 Abstract: Boron carbide is super-strong and has many important enginee… read more USED (low confidence) K. Reddy et al., “Dislocation-mediated shear amorphization in boron carbide,” Science Advances. 2021. link Times cited: 33 Abstract: A previously unidentified amorphization mechanism of boron c… read more USED (low confidence) M. Chen, Z. Liang, M. Liu, U. P. Kumar, C. Liu, and T. Liang, “First principles study of post-boron carbide phases with icosahedra broken,” Chinese Physics B. 2020. link Times cited: 2 USED (low confidence) L.-yuan Wang et al., “Novel superhard boron-rich nitrides under pressure,” Science China Materials. 2020. link Times cited: 14 USED (low confidence) A. Awasthi and G. Subhash, “Deformation behavior and amorphization in icosahedral boron-rich ceramics,” Progress in Materials Science. 2020. link Times cited: 30 USED (low confidence) O. Bystrenko et al., “Kinetics of bonds at structural breakdown in boron carbide under intensive loads: A molecular dynamics study,” Computational Materials Science. 2020. link Times cited: 2 USED (low confidence) J. Dai, J. Singh, and N. Yamamoto, “Fabrication and characterization of FAST sintered micro/nano boron carbide composites with enhanced fracture toughness,” Journal of the European Ceramic Society. 2020. link Times cited: 13 USED (low confidence) H. Luo, H. Zhang, H. Sheng, J. Liu, and I. Szlufarska, “Amorphous shear bands in SmCo5,” Materials Science and Engineering A-structural Materials Properties Microstructure and Processing. 2020. link Times cited: 12 USED (low confidence) J. Fuller and Q. An, “Room-Temperature Plastic Deformation in Diamond Nanopillars.” 2020. link Times cited: 3 USED (low confidence) Q. Yang, A. M. Celik, J. Du, J. LaSalvia, C. Hwang, and R. Haber, “Advancing the mechanical properties of Si/B co-doped boron carbide through TiB2 reinforcement,” Materials Letters. 2020. link Times cited: 11 USED (low confidence) M. Devries, G. Subhash, and A. Awasthi, “Shocked ceramics melt: An atomistic analysis of thermodynamic behavior of boron carbide,” Physical Review B. 2020. link Times cited: 17 Abstract: Macroscale experiments for structural response of materials … read more USED (low confidence) S. Xiang et al., “The effect of boron and aluminum additions on the microstructure of arc‐melted boron carbide,” Journal of the American Ceramic Society. 2020. link Times cited: 3 Abstract: In this work, B 4 C, B 4 C + 5 at.% Al, B 4 C + B, and B 4 C… read more USED (low confidence) N. Baishnab et al., “Role of generated free radicals in synthesis of amorphous hydrogenated boron carbide from orthocarborane using argon bombardment: a ReaxFF molecular dynamics study,” Materials Research Express. 2020. link Times cited: 0 Abstract: In this study, we modeled and analyzed a critical aspect of … read more USED (low confidence) R. Khadka, N. Baishnab, G. Opletal, and R. Sakidja, “Study of amorphous boron carbide (a-BxC) materials using Molecular Dynamics (MD) and Hybrid Reverse Monte Carlo (HRMC),” Journal of Non-crystalline Solids. 2020. link Times cited: 5 USED (low confidence) T. A. Yıldız and M. Durandurdu, “Amorphous boron carbide from ab initio simulations,” Computational Materials Science. 2020. link Times cited: 4 USED (low confidence) J. Gu et al., “Reactive sintering of B4C-TaB2 ceramics via carbide boronizing: Reaction process, microstructure and mechanical properties,” Journal of Materials Science & Technology. 2019. link Times cited: 19 USED (low confidence) Q. Yang et al., “Fabrication and characterization of arc melted Si/B co-doped boron carbide,” Journal of The European Ceramic Society. 2019. link Times cited: 13 USED (low confidence) A. Chauhan, X. Sun, K. Ramesh, and K. Hemker, “Dynamic failure mechanisms of granular boron carbide under multi-axial high-strain-rate loading,” Scripta Materialia. 2019. link Times cited: 9 USED (low confidence) A. Chauhan, M. Schaefer, R. Haber, and K. Hemker, “Experimental observations of amorphization in stoichiometric and boron-rich boron carbide,” Acta Materialia. 2019. link Times cited: 35 USED (low confidence) Z. Chao, T. T. Sun, L. Jiang, Z. Zhou, C. Guoqin, and G. Wu, “Ballistic behavior and microstructure evolution of B4C/AA2024 composites,” Ceramics International. 2019. link Times cited: 18 USED (low confidence) S. Xiang et al., “Tuning the deformation mechanisms of boron carbide via silicon doping,” Science Advances. 2019. link Times cited: 20 Abstract: Si-doped boron carbide could be a promising material for the… read more USED (low confidence) R. Zhang et al., “First-principles design of strong solids: Approaches and applications,” Physics Reports. 2019. link Times cited: 24 USED (low confidence) B. Yang et al., “Detwinning Mechanism for Nanotwinned Cubic Boron Nitride with Unprecedented Strength: A First-Principles Study,” Nanomaterials. 2019. link Times cited: 5 Abstract: Synthesized nanotwinned cubic boron nitride (nt-cBN) and nan… read more USED (low confidence) A. Chauhan, M. Schaefer, R. Haber, and K. Hemker, “Observed Mitigation of Local Amorphization in Boron-Rich Boron Carbide,” Materials Engineering eJournal. 2019. link Times cited: 3 Abstract: Boron carbide is extremely hard but has been shown to underg… read more USED (low confidence) J. D. Clayton, R. B. Leavy, and J. Knap, “Phase field modeling of heterogeneous microcrystalline ceramics,” International Journal of Solids and Structures. 2019. link Times cited: 14 USED (low confidence) D. Guo and Q. An, “Transgranular amorphous shear band formation in polycrystalline boron carbide,” International Journal of Plasticity. 2019. link Times cited: 12 USED (low confidence) A. Awasthi and G. Subhash, “High-pressure deformation and amorphization in boron carbide,” Journal of Applied Physics. 2019. link Times cited: 33 Abstract: Icosahedral boron-rich solids fall second in hardness to dia… read more USED (low confidence) M. Devries and G. Subhash, “Influence of carbon nanotubes as secondary phase addition on the mechanical properties and amorphization of boron carbide,” Journal of the European Ceramic Society. 2019. link Times cited: 19 USED (low confidence) Y. Shen, G. Li, and Q. An, “Enhanced fracture toughness of boron carbide from microalloying and nanotwinning,” Scripta Materialia. 2019. link Times cited: 21 USED (low confidence) Y. Shen and Q. An, “Brittle failure of orthorhombic borides from first-principles simulations,” Physical Review B. 2018. link Times cited: 1 USED (low confidence) J. Clayton and J. Knap, “Geometric micromechanical modeling of structure changes, fracture and grain boundary layers in polycrystals,” Journal of Micromechanics and Molecular Physics. 2018. link Times cited: 11 Abstract: A constitutive framework based on concepts from phase field … read more USED (low confidence) A. Khan et al., “Locating Si atoms in Si-doped boron carbide: A route to understand amorphization mitigation mechanism,” Acta Materialia. 2018. link Times cited: 34 USED (low confidence) S. Dyachkov, A. Parshikov, M. S. Egorova, S. Grigoryev, V. Zhakhovsky, and S. Medin, “Explicit failure model for boron carbide ceramics under shock loading,” Journal of Applied Physics. 2018. link Times cited: 11 Abstract: Ceramic materials have a long-term industrial demand due to … read more USED (low confidence) J. Clayton, “Generalized pseudo-Finsler geometry applied to the nonlinear mechanics of torsion of crystalline solids,” International Journal of Geometric Methods in Modern Physics. 2018. link Times cited: 8 Abstract: A continuum theory of the mechanical behavior of solid mater… read more USED (low confidence) J. Li, S. Xu, L. Liu, Z. Wang, J. Zhang, and Q. Liu, “Mechanism for amorphization of boron carbide under complex stress conditions,” Materials Research Express. 2018. link Times cited: 14 Abstract: As an excellent material, the application of boron carbide (… read more USED (low confidence) A. Ektarawong, “Thermodynamic consideration and ground-state search of icosahedral boron subselenide B 12 (B 1 -x Se x ) 2 from a first-principles cluster expansion,” Physical Review B. 2018. link Times cited: 2 Abstract: The phase stability of icosahedral boron subselenide B12(B1−… read more USED (low confidence) X. Yang, W. Goddard, and Q. An, “Asymmetric twins in boron rich boron carbide.,” Physical chemistry chemical physics : PCCP. 2018. link Times cited: 2 Abstract: Twin boundaries (TBs) play an essential role in enhancing th… read more USED (low confidence) Q. C. Liu and X. M. Zhou, “Time-resolved light emission of a, c, and r-cut sapphires shock-compressed to 65 GPa,” Journal of Applied Physics. 2018. link Times cited: 2 Abstract: To investigate light emission and dynamic deformation behavi… read more USED (low confidence) J. Knap and J. Clayton, “Continuum modeling of twinning, amorphization, and fracture: theory and numerical simulations,” Continuum Mechanics and Thermodynamics. 2018. link Times cited: 28 USED (low confidence) C. Kunka et al., “Nanotwinning and amorphization of boron suboxide,” Acta Materialia. 2018. link Times cited: 20 USED (low confidence) X. Yang, S. Coleman, J. LaSalvia, W. Goddard, and Q. An, “Shear-Induced Brittle Failure along Grain Boundaries in Boron Carbide.,” ACS applied materials & interfaces. 2018. link Times cited: 21 Abstract: The role that grain boundaries (GBs) can play on mechanical … read more USED (low confidence) Y. You, K. Yoshida, T. Inoue, and T. Yano, “Helium bubbles and trace of lithium in B4C control rod pellets used in JOYO experimental fast reactor,” Journal of Nuclear Science and Technology. 2018. link Times cited: 7 Abstract: ABSTRACT B4C pellets used in the control rod of the experime… read more USED (low confidence) J. Clayton and J. Knap, “Continuum modeling of twinning, amorphization, and fracture: theory and numerical simulations,” Continuum Mechanics and Thermodynamics. 2017. link Times cited: 0 USED (low confidence) K. L. Joshi and S. Chaudhuri, “Observation of deflagration wave in energetic materials using reactive molecular dynamics,” Combustion and Flame. 2017. link Times cited: 17 USED (low confidence) K. Xie et al., “Microstructural characterization of boron-rich boron carbide,” Acta Materialia. 2017. link Times cited: 81 USED (low confidence) Q. An and W. Goddard, “Ductility in Crystalline Boron Subphosphide (B12P2) for Large Strain Indentation,” Journal of Physical Chemistry C. 2017. link Times cited: 14 Abstract: Our studies of brittle fracture in B4C showed that shear-ind… read more USED (low confidence) Q. An and W. Goddard, “Improved Ductility of B12 Icosahedra-based Superhard Materials through Icosahedral Slip,” Journal of Physical Chemistry C. 2017. link Times cited: 12 Abstract: Boron carbide (B4C) is superhard but suffers from brittle fa… read more USED (low confidence) J. Clayton and J. Clayton, “Finsler-geometric continuum dynamics and shock compression,” International Journal of Fracture. 2017. link Times cited: 17 USED (low confidence) J. Li et al., “Ab initio study on the anisotropy of mechanical behavior and deformation mechanism for boron carbide,” Chinese Physics B. 2017. link Times cited: 11 USED (low confidence) Q. An and W. Goddard, “Nanotwins soften boron-rich boron carbide (B13C2),” Applied Physics Letters. 2017. link Times cited: 30 Abstract: Extensive studies of metals and alloys have observed that na… read more USED (low confidence) P. Pokatashkin, P. Korotaev, and A. Yanilkin, “Amorphization in .ALPHA.-boron: A molecular dynamics study,” Physical Review B. 2017. link Times cited: 3 USED (low confidence) Q. An et al., “Superstrength through Nanotwinning.,” Nano letters. 2016. link Times cited: 60 Abstract: The theoretical strength of a material is the minimum stress… read more USED (low confidence) S. Zhao et al., “Directional amorphization of boron carbide subjected to laser shock compression,” Proceedings of the National Academy of Sciences. 2016. link Times cited: 86 Abstract: Significance When crystalline solids are stressed quasi-stat… read more USED (low confidence) J. Clayton, “Finsler-Geometric Continuum Mechanics and the Micromechanics of Fracture in Crystals.” 2016. link Times cited: 18 Abstract: A continuum theory for the mechanical response of solid bodi… read more USED (low confidence) C. Kunka, A. Awasthi, and G. Subhash, “Crystallographic and spectral equivalence of boron-carbide polymorphs,” Scripta Materialia. 2016. link Times cited: 19 USED (low confidence) Q. An, M. R. Kolan, H. Dong, M.-W. Chen, A. R. Oganov, and W. A. Goddard, “Nanotwinned Boron Suboxide (B6O): New Ground State of B6O.,” Nano letters. 2016. link Times cited: 42 Abstract: Nanotwinned structures in superhard ceramics rhombohedral bo… read more USED (low confidence) S. Coleman, E. Hernández-Rivera, K. Behler, J. Synowczynski-Dunn, and M. Tschopp, “Challenges of Engineering Grain Boundaries in Boron-Based Armor Ceramics,” JOM. 2016. link Times cited: 13 USED (low confidence) B. Tang, Q. An, and W. Goddard, “Improved Ductility of Boron Carbide by Microalloying with Boron Suboxide,” Journal of Physical Chemistry C. 2015. link Times cited: 26 Abstract: Boron carbide (B_4C) is the third hardest material in nature… read more USED (low confidence) J. Clayton, “Computational Modeling of Dual-Phase Ceramics withFinsler-Geometric Phase Field Mechanics,” Cmes-computer Modeling in Engineering & Sciences. 2019. link Times cited: 6 Abstract: A theory invoking concepts from differential geometry of gen… read more USED (low confidence) J. Clayton, “Fracture and Flow in Brittle Solids,” Shock Wave and High Pressure Phenomena. 2019. link Times cited: 0 USED (low confidence) J. Clayton, “Finsler-Geometric Modeling of Structural Changes in Solids,” Shock Wave and High Pressure Phenomena. 2019. link Times cited: 0 USED (low confidence) J. Clayton, R. B. Leavy, and J. Knap, “Mesoscale Modeling of Microcrystalline Ceramics,” International Conference on Computational & Experimental Engineering and Sciences. 2019. link Times cited: 0 Abstract: : Diffuse interface models and simulations capture deformati… read more NOT USED (low confidence) Z. Zheng, T. Xu, D. Legut, and R. Zhang, “High-throughput informed machine learning models for ultrastrong B-N solids,” Computational Materials Science. 2022. link Times cited: 2 NOT USED (low confidence) Q. Zeng, A. Tonge, and K. Ramesh, “A multi-mechanism constitutive model for the dynamic failure of quasi-brittle materials. Part II: Integrative model,” Journal of the Mechanics and Physics of Solids. 2019. link Times cited: 13 NOT USED (low confidence) Q. Zeng, A. Tonge, and K. Ramesh, “A multi-mechanism constitutive model for the dynamic failure of quasi-brittle materials. Part I: Amorphization as a failure mode,” Journal of the Mechanics and Physics of Solids. 2019. link Times cited: 19 NOT USED (low confidence) E. Hernández-Rivera, S. Chowdhury, S. Coleman, P. Ghassemi, and M. Tschopp, “Integrating exploratory data analytics into ReaxFF parameterization,” MRS Communications. 2018. link Times cited: 0 Abstract: We present a systematic approach to refine hyperdimensional … read more NOT USED (low confidence) J. Lim, H. Kim, K. Cho, and M. Cho, “Fundamental mechanisms of fracture and its suppression in Ni-rich layered cathodes: Mechanics-based multiscale approaches,” Extreme Mechanics Letters. 2018. link Times cited: 16 NOT USED (low confidence) J. D. Clayton and J. D. Clayton, “Generalized Finsler geometric continuum physics with applications in fracture and phase transformations,” Zeitschrift für angewandte Mathematik und Physik. 2017. link Times cited: 26 NOT USED (low confidence) J. Clayton, “Generalized Finsler geometric continuum physics with applications in fracture and phase transformations,” Zeitschrift für angewandte Mathematik und Physik. 2016. link Times cited: 0 NOT USED (high confidence) A. Rau, S. Jubin, J. R. Vella, and I. Kaganovich, “Simulations of graphite boronization: A molecular dynamics study of amorphization resulting from bombardment,” Frontiers of Physics. 2022. link Times cited: 0 Abstract: The molecular dynamics code LAMMPS was used to simulate the … read more NOT USED (high confidence) S. Jubin, A. Rau, Y. Barsukov, S. Ethier, and I. Kaganovich, “Boron adatom adsorption on graphene: A case study in computational chemistry methods for surface interactions,” Frontiers of Physics. 2022. link Times cited: 4 Abstract: Though weak surface interactions and adsorption can play an … read more NOT USED (high confidence) D. Guo et al., “Grain Boundary Sliding and Amorphization are Responsible for the Reverse Hall-Petch Relation in Superhard Nanocrystalline Boron Carbide.,” Physical review letters. 2018. link Times cited: 58 Abstract: The recent observation of the reverse Hall-Petch relation in… read more NOT USED (high confidence) G. Subhash, A. Awasthi, C. Kunka, P. Jannotti, and M. Devries, “In search of amorphization-resistant boron carbide,” Scripta Materialia. 2016. link Times cited: 59 NOT USED (high confidence) Q. An, K. Reddy, J. Qian, K. Hemker, M.-W. Chen, and W. G. III, “Nucleation of amorphous shear bands at nanotwins in boron suboxide,” Nature Communications. 2016. link Times cited: 37 |
| Funding | Not available |
| Short KIM ID
The unique KIM identifier code.
| SM_389039364091_000 |
| Extended KIM ID
The long form of the KIM ID including a human readable prefix (100 characters max), two underscores, and the Short KIM ID. Extended KIM IDs can only contain alpha-numeric characters (letters and digits) and underscores and must begin with a letter.
| Sim_LAMMPS_ReaxFF_AnGoddard_2015_BC__SM_389039364091_000 |
| DOI |
10.25950/d253fc36 https://doi.org/10.25950/d253fc36 https://commons.datacite.org/doi.org/10.25950/d253fc36 |
| KIM Item Type | Simulator Model |
| KIM API Version | 2.2 |
| Simulator Name
The name of the simulator as defined in kimspec.edn.
| LAMMPS |
| Potential Type | reax |
| Simulator Potential | reaxff |
| Run Compatibility | portable-models |
| Grade | Name | Category | Brief Description | Full Results | Aux File(s) |
|---|---|---|---|---|---|
| P | vc-species-supported-as-stated | mandatory | The model supports all species it claims to support; see full description. |
Results | Files |
| P | vc-periodicity-support | mandatory | Periodic boundary conditions are handled correctly; see full description. |
Results | Files |
| F | vc-permutation-symmetry | mandatory | Total energy and forces are unchanged when swapping atoms of the same species; see full description. |
Results | Files |
| D | vc-forces-numerical-derivative | consistency | Forces computed by the model agree with numerical derivatives of the energy; see full description. |
Results | Files |
| F | vc-dimer-continuity-c1 | informational | The energy versus separation relation of a pair of atoms is C1 continuous (i.e. the function and its first derivative are continuous); see full description. |
Results | Files |
| P | vc-objectivity | informational | Total energy is unchanged and forces transform correctly under rigid-body translation and rotation; see full description. |
Results | Files |
| P | vc-inversion-symmetry | informational | Total energy is unchanged and forces change sign when inverting a configuration through the origin; see full description. |
Results | Files |
| F | vc-memory-leak | informational | The model code does not have memory leaks (i.e. it releases all allocated memory at the end); see full description. |
Results | Files |
| N/A | vc-thread-safe | mandatory | The model returns the same energy and forces when computed in serial and when using parallel threads for a set of configurations. Note that this is not a guarantee of thread safety; see full description. |
Results | Files |
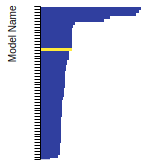
BCC Lattice Constant
This bar chart plot shows the mono-atomic body-centered cubic (bcc) lattice constant predicted by the current model (shown in the unique color) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
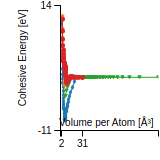
Cohesive Energy Graph
This graph shows the cohesive energy versus volume-per-atom for the current mode for four mono-atomic cubic phases (body-centered cubic (bcc), face-centered cubic (fcc), simple cubic (sc), and diamond). The curve with the lowest minimum is the ground state of the crystal if stable. (The crystal structure is enforced in these calculations, so the phase may not be stable.) Graphs are generated for each species supported by the model.
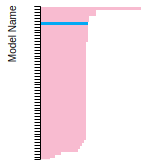
Diamond Lattice Constant
This bar chart plot shows the mono-atomic face-centered diamond lattice constant predicted by the current model (shown in the unique color) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
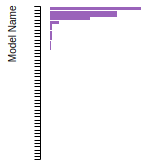
Dislocation Core Energies
This graph shows the dislocation core energy of a cubic crystal at zero temperature and pressure for a specific set of dislocation core cutoff radii. After obtaining the total energy of the system from conjugate gradient minimizations, non-singular, isotropic and anisotropic elasticity are applied to obtain the dislocation core energy for each of these supercells with different dipole distances. Graphs are generated for each species supported by the model.
(No matching species)FCC Elastic Constants
This bar chart plot shows the mono-atomic face-centered cubic (fcc) elastic constants predicted by the current model (shown in blue) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
FCC Lattice Constant
This bar chart plot shows the mono-atomic face-centered cubic (fcc) lattice constant predicted by the current model (shown in red) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
FCC Stacking Fault Energies
This bar chart plot shows the intrinsic and extrinsic stacking fault energies as well as the unstable stacking and unstable twinning energies for face-centered cubic (fcc) predicted by the current model (shown in blue) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
(No matching species)FCC Surface Energies
This bar chart plot shows the mono-atomic face-centered cubic (fcc) relaxed surface energies predicted by the current model (shown in blue) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
(No matching species)SC Lattice Constant
This bar chart plot shows the mono-atomic simple cubic (sc) lattice constant predicted by the current model (shown in the unique color) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
Cubic Crystal Basic Properties Table
Species: BSpecies: C
Creators:
Contributor: karls
Publication Year: 2019
DOI: https://doi.org/10.25950/64cb38c5
This Test Driver uses LAMMPS to compute the cohesive energy of a given monoatomic cubic lattice (fcc, bcc, sc, or diamond) at a variety of lattice spacings. The lattice spacings range from a_min (=a_min_frac*a_0) to a_max (=a_max_frac*a_0) where a_0, a_min_frac, and a_max_frac are read from stdin (a_0 is typically approximately equal to the equilibrium lattice constant). The precise scaling and number of lattice spacings sampled between a_min and a_0 (a_0 and a_max) is specified by two additional parameters passed from stdin: N_lower and samplespacing_lower (N_upper and samplespacing_upper). Please see README.txt for further details.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Cohesive energy versus lattice constant curve for bcc C v004 | view | 37473 | |
| Cohesive energy versus lattice constant curve for diamond C v004 | view | 40092 | |
| Cohesive energy versus lattice constant curve for fcc C v004 | view | 26128 | |
| Cohesive energy versus lattice constant curve for sc C v004 | view | 5540 |
Creators: Junhao Li and Ellad Tadmor
Contributor: tadmor
Publication Year: 2019
DOI: https://doi.org/10.25950/5853fb8f
Computes the cubic elastic constants for some common crystal types (fcc, bcc, sc, diamond) by calculating the hessian of the energy density with respect to strain. An estimate of the error associated with the numerical differentiation performed is reported.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Elastic constants for diamond C at zero temperature v001 | view | 2989434 | |
| Elastic constants for fcc C at zero temperature v006 | view | 107339 | |
| Elastic constants for sc C at zero temperature v006 | view | 32688 |
Creators:
Contributor: ilia
Publication Year: 2024
DOI: https://doi.org/10.25950/2f2c4ad3
Computes the equilibrium crystal structure and energy for an arbitrary crystal at zero temperature and applied stress by performing symmetry-constrained relaxation. The crystal structure is specified using the AFLOW prototype designation. Multiple sets of free parameters corresponding to the crystal prototype may be specified as initial guesses for structure optimization. No guarantee is made regarding the stability of computed equilibria, nor that any are the ground state.
Creators: Ilia Nikiforov
Contributor: ilia
Publication Year: 2019
DOI: https://doi.org/10.25950/dd36239b
Given atomic species and structure type (graphene-like, 2H, or 1T) of a 2D hexagonal monolayer crystal, as well as an initial guess at the lattice spacing, this Test Driver calculates the equilibrium lattice spacing and cohesive energy using Polak-Ribiere conjugate gradient minimization in LAMMPS
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Cohesive energy and equilibrium lattice constant of graphene v002 | view | 1104 |
Creators: Daniel S. Karls and Junhao Li
Contributor: karls
Publication Year: 2019
DOI: https://doi.org/10.25950/2765e3bf
Equilibrium lattice constant and cohesive energy of a cubic lattice at zero temperature and pressure.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Equilibrium zero-temperature lattice constant for bcc C v007 | view | 26724 | |
| Equilibrium zero-temperature lattice constant for diamond C v007 | view | 88418 | |
| Equilibrium zero-temperature lattice constant for fcc C v007 | view | 41080 | |
| Equilibrium zero-temperature lattice constant for sc C v007 | view | 13676 |
Creators: Daniel S. Karls and Junhao Li
Contributor: karls
Publication Year: 2019
DOI: https://doi.org/10.25950/c339ca32
Calculates lattice constant of hexagonal bulk structures at zero temperature and pressure by using simplex minimization to minimize the potential energy.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Equilibrium lattice constants for hcp B v005 | view | 432512 | |
| Equilibrium lattice constants for hcp C v005 | view | 797678 |
| Test | Error Categories | Link to Error page |
|---|---|---|
| Elastic constants for bcc C at zero temperature v006 | other | view |
ElasticConstantsHexagonal__TD_612503193866_004
| Test | Error Categories | Link to Error page |
|---|---|---|
| Elastic constants for hcp B at zero temperature v004 | other | view |
| Elastic constants for hcp C at zero temperature v004 | other | view |
EquilibriumCrystalStructure__TD_457028483760_000
EquilibriumCrystalStructure__TD_457028483760_002
LatticeConstantCubicEnergy__TD_475411767977_007
| Test | Error Categories | Link to Error page |
|---|---|---|
| Equilibrium zero-temperature lattice constant for bcc B v007 | other | view |
| Equilibrium zero-temperature lattice constant for diamond B v007 | other | view |
| Equilibrium zero-temperature lattice constant for fcc B v007 | other | view |
| Equilibrium zero-temperature lattice constant for sc B v007 | other | view |
LinearThermalExpansionCoeffCubic__TD_522633393614_001
| Test | Error Categories | Link to Error page |
|---|---|---|
| Linear thermal expansion coefficient of diamond C at 293.15 K under a pressure of 0 MPa v001 | other | view |
| Sim_LAMMPS_ReaxFF_AnGoddard_2015_BC__SM_389039364091_000.txz | Tar+XZ | Linux and OS X archive |
| Sim_LAMMPS_ReaxFF_AnGoddard_2015_BC__SM_389039364091_000.zip | Zip | Windows archive |