SW_ZhouWardMartin_2013_CdTeZnSeHgS__MO_503261197030_003
SW_ZhouWardMartin_2013_CdTeZnSeHgS__MO_503261197030_003
Use this Potential
| Title
A single sentence description.
|
Stillinger-Weber potential for the Zn-Cd-Hg-S-Se-Te system developed by Zhou et al. (2013) v003 |
|---|---|
| Description
A short description of the Model describing its key features including for example: type of model (pair potential, 3-body potential, EAM, etc.), modeled species (Ac, Ag, ..., Zr), intended purpose, origin, and so on.
|
Bulk and multilayered thin film crystals of II-VI semiconductor compounds are the leading materials for infrared sensing, gamma-ray detection, photovoltaics, and quantum dot lighting applications. The key to achieving high performance for these applications is reducing crystallographic defects. Unfortunately, past efforts to improve these materials have been prolonged due to a lack of understanding with regards to defect formation and evolution mechanisms. To enable high-fidelity and high-efficiency atomistic simulations of defect mechanisms, this paper develops a Stillinger-Weber interatomic potential database for semiconductor compounds composed of the major II-VI elements Zn, Cd, Hg, S, Se, and Te. The potential's fidelity is achieved by optimizing all the pertinent model parameters, by imposing reasonable energy trends to correctly capture the transformation between elemental, solid solution, and compound phases, and by capturing exactly the experimental cohesive energies, lattice constants, and bulk moduli of all binary compounds. Verification tests indicate that our model correctly predicts crystalline growth of all binary compounds during molecular dynamics simulations of vapor deposition. Two stringent cases convincingly show that our potential is applicable for a variety of compound configurations involving all the six elements considered here. In the first case, we demonstrate a successful molecular dynamics simulation of crystalline growth of an alloyed (Cd_0.28Zn_0.68Hg_0.04) (Te_0.20Se_0.18S_0.62) compound on a ZnS substrate. In the second case, we demonstrate the predictive power of our model on defects, such as misfit dislocations, stacking faults, and subgrain nucleation, using a complex growth simulation of ZnS/CdSe/HgTe multilayers that also contain all the six elements considered here. Using CdTe as a case study, a comprehensive comparison of our potential with literature potentials is also made. Finally, we also propose unique insights for improving the Stillinger-Weber potential in future developments. |
| Species
The supported atomic species.
| Cd, Hg, S, Se, Te, Zn |
| Disclaimer
A statement of applicability provided by the contributor, informing users of the intended use of this KIM Item.
|
None |
| Contributor |
Mingjian Wen |
| Maintainer |
Mingjian Wen |
| Implementer | Mingjian Wen |
| Developer |
Xiaowang Zhou Donald K. Ward J. E. Martin F. B. van Swol J.L. Cruz-Campa D. Zubia |
| Published on KIM | 2021 |
| How to Cite |
This Model originally published in [1-3] is archived in OpenKIM [4-7]. [1] Stillinger FH, Weber TA. Computer simulation of local order in condensed phases of silicon. Physical Review B. 1985Apr;31(8):5262–71. doi:10.1103/PhysRevB.31.5262 [2] Tadmor EB, Miller RE. Modeling Materials: Continuum, Atomistic and Multiscale Techniques. Cambridge University Press; 2011. [3] Zhou XW, Ward DK, Martin JE, Swol FB van, Cruz-Campa JL, Zubia D. Stillinger–Weber potential for the II-VI elements Zn-Cd-Hg-S-Se-Te. Physical Review B. 2013Aug;88(8):085309. doi:10.1103/PhysRevB.88.085309 — (Primary Source) A primary source is a reference directly related to the item documenting its development, as opposed to other sources that are provided as background information. [4] Wen M, Zhou X, Ward DK, Martin JE, Swol FB van, Cruz-Campa JL, et al. Stillinger-Weber potential for the Zn-Cd-Hg-S-Se-Te system developed by Zhou et al. (2013) v003. OpenKIM; 2021. doi:10.25950/8846e83d [5] Wen M, Afshar Y, Stillinger FH, Weber TA. Stillinger-Weber (SW) Model Driver v005. OpenKIM; 2021. doi:10.25950/934dca3e [6] Tadmor EB, Elliott RS, Sethna JP, Miller RE, Becker CA. The potential of atomistic simulations and the Knowledgebase of Interatomic Models. JOM. 2011;63(7):17. doi:10.1007/s11837-011-0102-6 [7] Elliott RS, Tadmor EB. Knowledgebase of Interatomic Models (KIM) Application Programming Interface (API). OpenKIM; 2011. doi:10.25950/ff8f563a Click here to download the above citation in BibTeX format. |
| Citations
This panel presents information regarding the papers that have cited the interatomic potential (IP) whose page you are on. The OpenKIM machine learning based Deep Citation framework is used to determine whether the citing article actually used the IP in computations (denoted by "USED") or only provides it as a background citation (denoted by "NOT USED"). For more details on Deep Citation and how to work with this panel, click the documentation link at the top of the panel. The word cloud to the right is generated from the abstracts of IP principle source(s) (given below in "How to Cite") and the citing articles that were determined to have used the IP in order to provide users with a quick sense of the types of physical phenomena to which this IP is applied. The bar chart shows the number of articles that cited the IP per year. Each bar is divided into green (articles that USED the IP) and blue (articles that did NOT USE the IP). Users are encouraged to correct Deep Citation errors in determination by clicking the speech icon next to a citing article and providing updated information. This will be integrated into the next Deep Citation learning cycle, which occurs on a regular basis. OpenKIM acknowledges the support of the Allen Institute for AI through the Semantic Scholar project for providing citation information and full text of articles when available, which are used to train the Deep Citation ML algorithm. |
This panel provides information on past usage of this interatomic potential (IP) powered by the OpenKIM Deep Citation framework. The word cloud indicates typical applications of the potential. The bar chart shows citations per year of this IP (bars are divided into articles that used the IP (green) and those that did not (blue)). The complete list of articles that cited this IP is provided below along with the Deep Citation determination on usage. See the Deep Citation documentation for more information. 
78 Citations (56 used)
Help us to determine which of the papers that cite this potential actually used it to perform calculations. If you know, click the .
USED (definite) R. Aguirre, S. Abdullah, X. W. Zhou, and D. Zubia, “Molecular Dynamics Calculations of Grain Boundary Mobility in CdTe,” Nanomaterials. 2019. link Times cited: 4 Abstract: Molecular dynamics (MD) simulations have been applied to stu… read more USED (definite) X. W. Zhou and S. Foiles, “Uncertainty Quantification and Reduction of Molecular Dynamics Models.” 2017. link Times cited: 9 Abstract: Molecular dynamics (MD) is an important method underlying th… read more USED (definite) J. J. Chavez, X. W. Zhou, S. Almeida, R. Aguirre, and D. Zubia, “Molecular Dynamics Simulations of CdTe / CdS Heteroepitaxy - Effect of Substrate Orientation,” Journal of Materials Science Research. 2016. link Times cited: 11 Abstract: Molecular dynamics simulations were used to catalogue atomic… read more USED (definite) S. Almeida, E. Ochoa, J. J. Chavez, X. W. Zhou, and D. Zubia, “Calculation of surface diffusivity and residence time by molecular dynamics with application to nanoscale selective-area growth,” Journal of Crystal Growth. 2015. link Times cited: 3 USED (definite) Z. Zhang et al., “Deformation twinning evolution from a single crystal in a face-centered-cubic ternary alloy,” Scientific Reports. 2015. link Times cited: 19 USED (high confidence) P. Brosseau, J. Geuchies, D. Jasrasaria, A. Houtepen, E. Rabani, and P. Kambhampati, “Ultrafast hole relaxation dynamics in quantum dots revealed by two-dimensional electronic spectroscopy,” Communications Physics. 2023. link Times cited: 5 USED (high confidence) D. Jasrasaria and E. Rabani, “Circumventing the phonon bottleneck by multiphonon-mediated hot exciton cooling at the nanoscale,” npj Computational Materials. 2023. link Times cited: 1 USED (high confidence) B. Hou, M. Thoss, U. Banin, and E. Rabani, “Incoherent nonadiabatic to coherent adiabatic transition of electron transfer in colloidal quantum dot molecules,” Nature Communications. 2022. link Times cited: 2 USED (high confidence) M. Wen, Y. Afshar, R. Elliott, and E. Tadmor, “KLIFF: A framework to develop physics-based and machine learning interatomic potentials,” Comput. Phys. Commun. 2021. link Times cited: 12 USED (high confidence) H. Huan, B. Fu, and X. Ye, “Tuning the thermal conductivity of wurtzite CdSe nanowires: effects of size, strain, torsion and temperature,” Philosophical Magazine. 2021. link Times cited: 1 Abstract: ABSTRACT The thermal transport of wurtzite CdSe nanowires (N… read more USED (high confidence) C. Yan et al., “Uncovering the Role of Hole Traps in Promoting Hole Transfer from Multiexcitonic Quantum Dots to Molecular Acceptors.,” ACS nano. 2020. link Times cited: 17 Abstract: Understanding electronic dynamics in multiexcitonic quantum … read more USED (high confidence) S. Goel et al., “Horizons of modern molecular dynamics simulation in digitalized solid freeform fabrication with advanced materials,” Materials Today Chemistry. 2020. link Times cited: 17 USED (high confidence) S. Abdullah, R. Aguirre, X. W. Zhou, and D. Zubia, “Growth Evolution of Polycrystalline CdTe/CdS with Atomic Scale Resolution via Molecular Dynamics,” 2019 IEEE 46th Photovoltaic Specialists Conference (PVSC). 2019. link Times cited: 1 Abstract: A new method to study polycrystalline growth of CdTe layers … read more USED (high confidence) R. Aguirre et al., “Crystal Growth and Atom Diffusion in (Cu)ZnTe/CdTe via Molecular Dynamics,” IEEE Journal of Photovoltaics. 2018. link Times cited: 4 Abstract: Molecular dynamics (MD) simulations and experimental evapora… read more USED (high confidence) M. Yu and S. Kenny, “Modelling the deposition process on the CdTe/CdS interface,” Nuclear Instruments & Methods in Physics Research Section B-beam Interactions With Materials and Atoms. 2017. link Times cited: 1 USED (high confidence) X. W. Zhou, J. J. Chavez, S. Almeida, and D. Zubia, “Understanding misfit strain releasing mechanisms via molecular dynamics simulations of CdTe growth on 112zinc-blende CdS,” Journal of Applied Physics. 2016. link Times cited: 11 Abstract: Molecular dynamics simulations have been used to analyse mic… read more USED (high confidence) S. Almeida, J. J. Chavez, X. W. Zhou, and D. Zubia, “Effect of substrate orientation on CdS homoepitaxy by molecular dynamics,” Journal of Crystal Growth. 2016. link Times cited: 4 USED (high confidence) F. van Swol, X. W. Zhou, S. R. Challa, and J. E. Martin, “Heterojunctions of model CdTe/CdSe mixtures,” Modelling and Simulation in Materials Science and Engineering. 2015. link Times cited: 0 Abstract: We report on the strain behavior of compound mixtures of mod… read more USED (high confidence) J. J. Chavez, X. W. Zhou, D. Ward, J. Cruz-Campa, and D. Zubia, “A molecular dynamics study on defect reduction in thin film Cd1−xZnxTe/CdS solar cells,” 2014 IEEE 40th Photovoltaic Specialist Conference (PVSC). 2014. link Times cited: 1 Abstract: Recently developed molecular dynamics models have been appli… read more USED (low confidence) C. Liu, W. Yip, S. To, B. Chen, and J. Xu, “Numerical Investigation on the Effects of Grain Size and Grinding Depth on Nano-Grinding of Cadmium Telluride Using Molecular Dynamics Simulation,” Nanomaterials. 2023. link Times cited: 0 Abstract: Cadmium telluride (CdTe) is known as an important semiconduc… read more USED (low confidence) K. Peng and E. Rabani, “Polaritonic Bottleneck in Colloidal Quantum Dots.,” Nano letters. 2023. link Times cited: 0 Abstract: Controlling the relaxation dynamics of excitons is key to im… read more USED (low confidence) N. A. Pike and R. Pachter, “Fitting the charged-optimized many-body potential for the Al-O-Se-Zn system,” Computational Materials Science. 2023. link Times cited: 0 USED (low confidence) Y. Li, B. Gu, A. Diaz, S. Phillpot, D. McDowell, and Y. Chen, “Dislocation formation in the heteroepitaxial growth of PbSe/PbTe systems,” Acta Materialia. 2023. link Times cited: 2 USED (low confidence) A. Islam, M. S. Hasan, M. S. Islam, A. G. Bhuiyan, C. Stampfl, and J. Park, “Crystal orientation-dependent tensile mechanical behavior and deformation mechanisms of zinc-blende ZnSe nanowires,” Scientific Reports. 2023. link Times cited: 0 USED (low confidence) K. Lin, D. Jasrasaria, J. Yoo, M. Bawendi, H. Utzat, and E. Rabani, “Theory of Photoluminescence Spectral Line Shapes of Semiconductor Nanocrystals.,” The journal of physical chemistry letters. 2022. link Times cited: 3 Abstract: Single-molecule photoluminescence (PL) spectroscopy of semic… read more USED (low confidence) C. Xu et al., “Anisotropic mechanical responses and plastic deformation mechanisms of cadmium telluride under indentations,” Applied Physics A. 2022. link Times cited: 2 USED (low confidence) Y. Li, Z. Zheng, A. Diaz, S. Phillpot, D. McDowell, and Y. Chen, “Resonant interaction between phonons and PbTe/PbSe (001) misfit dislocation networks,” Acta Materialia. 2022. link Times cited: 4 USED (low confidence) S. Abdullah, X. W. Zhou, R. Aguirre, and D. Zubia, “A computational approach to analyze grain structures of semiconductor compound films: Case study of CdTe/CdS multilayers,” MRS Advances. 2022. link Times cited: 0 Abstract: Grain structures impact the performance of semiconductor dev… read more USED (low confidence) A. Islam, M. S. Hasan, M. S. Islam, and J. Park, “Chirality, temperature, and vacancy effects on mechanical behavior of monolayer zinc-sulfide,” Computational Materials Science. 2021. link Times cited: 3 USED (low confidence) C. Xu, F.-ming Liu, C. Liu, P. Wang, and H. Liu, “Orientation Dependent Mechanical Responses and Plastic Deformation Mechanisms of ZnSe Nano Films under Nanoindentation,” Nanomaterials. 2021. link Times cited: 3 Abstract: Although ZnSe has been widely studied due to its attractive … read more USED (low confidence) J. Chen and X. Zhang, “Thermal resistance and thermal rectification of silicon device with triangular pores: A molecular dynamics study,” Physics Letters A. 2021. link Times cited: 1 USED (low confidence) P. Hu, S. Wang, and Y. Zhuo, “Research on operation parameters and properties of flue gas on adsorption of As2O3 by γ-Al2O3: An experiment and simulation study,” Process Safety and Environmental Protection. 2021. link Times cited: 10 USED (low confidence) A. Islam, M. S. Islam, M. R. Islam, C. Stampfl, and J. Park, “Thermal transport in monolayer zinc-sulfide: effects of length, temperature and vacancy defects,” Nanotechnology. 2021. link Times cited: 5 Abstract: Of late, atomically thin two-dimensional zinc-sulfide (2D-Zn… read more USED (low confidence) M. Rahman, E. Chowdhury, D. A. Redwan, and S. Hong, “Computational characterization of thermal and mechanical properties of single and bilayer germanene nanoribbon,” Computational Materials Science. 2021. link Times cited: 13 USED (low confidence) N. Hew, D. Spagnoli, and L. Faraone, “Dislocation core energies of the 0° perfect, 60° perfect, 30° partial, and 90° partial dislocations in CdTe, HgTe, and ZnTe: A molecular statics and elasticity theory analysis,” Materials today communications. 2021. link Times cited: 3 USED (low confidence) J. C. Ondry, J. Philbin, M. Lostica, E. Rabani, and A. Alivisatos, “Colloidal Synthesis Path to 2D Crystalline Quantum Dot Superlattices.,” ACS nano. 2020. link Times cited: 28 Abstract: By combining colloidal nanocrystal synthesis, self-assembly,… read more USED (low confidence) D. P. Rai, A. Laref, M. Khuili, S. Al-Qaisi, T. Vu, and D. D. Vo, “Electronic, magnetic and optical properties of monolayer (ML) hexagonal ZnSe on vacancy defects at Zn sites from DFT-1/2 approach,” Vacuum. 2020. link Times cited: 13 USED (low confidence) J. Philbin and E. Rabani, “Auger Recombination Lifetime Scaling for Type-I and Quasi-Type-II Core/Shell Quantum Dots.,” The journal of physical chemistry letters. 2020. link Times cited: 22 Abstract: Having already achieved near-unity quantum yields, with prom… read more USED (low confidence) B. Chettri et al., “Induced ferromagnetism in bilayer hexagonal Boron Nitride (h-BN) on vacancy defects at B and N sites,” arXiv: Materials Science. 2020. link Times cited: 16 USED (low confidence) R. Khadka, N. Baishnab, G. Opletal, and R. Sakidja, “Study of amorphous boron carbide (a-BxC) materials using Molecular Dynamics (MD) and Hybrid Reverse Monte Carlo (HRMC),” Journal of Non-crystalline Solids. 2020. link Times cited: 5 USED (low confidence) H. Abbas and J. Hahn, “Crystallization mechanism of liquid tellurium from classical molecular dynamics simulation,” Materials Chemistry and Physics. 2020. link Times cited: 6 USED (low confidence) X. W. Zhou, “Impact of Molecular Dynamics Simulations on Research and Development of Semiconductor Materials,” MRS Advances. 2019. link Times cited: 2 Abstract: Atomic scale defects critically limit performance of semicon… read more USED (low confidence) J. C. Ondry et al., “Resilient Pathways to Atomic Attachment of Quantum Dot Dimers and Artificial Solids from Faceted CdSe Quantum Dot Building Blocks.,” ACS nano. 2019. link Times cited: 25 Abstract: The goal of this work is to identify favored pathways for pr… read more USED (low confidence) C. Chen, P. Song, F. Meng, P. Ou, X. Liu, and J. Song, “Predictive modeling of misfit dislocation induced strain relaxation effect on self-rolling of strain-engineered nanomembranes,” Applied Physics Letters. 2018. link Times cited: 2 Abstract: Combining atomistic simulations and continuum modeling, the … read more USED (low confidence) T. Majdi, S. Pal, A. Hafreager, S. Murad, R. Sahu, and I. Puri, “Altering thermal transport by strained-layer epitaxy,” Applied Physics Letters. 2018. link Times cited: 4 Abstract: Since strain changes the interatomic spacing of matter and a… read more USED (low confidence) B. Bonef et al., “High spatial resolution correlated investigation of Zn segregation to stacking faults in ZnTe/CdSe nanostructures,” Applied Physics Letters. 2018. link Times cited: 4 Abstract: The correlative use of atom probe tomography (APT) and energ… read more USED (low confidence) X. Qian, X. Gu, and R. Yang, “Thermal conductivity modeling of hybrid organic-inorganic crystals and superlattices,” Nano Energy. 2017. link Times cited: 31 USED (low confidence) R. Aguirre, J. J. Chavez, X. W. Zhou, and D. Zubia, “High Fidelity Polycrystalline CdTe/CdS Heterostructures via Molecular Dynamics,” MRS Advances. 2017. link Times cited: 3 Abstract: Molecular dynamics simulations of polycrystalline growth of … read more USED (low confidence) Q. Xiang et al., “Deformation mechanisms and twin boundary effects in cadmium telluride under nanoindentation,” Ceramics International. 2017. link Times cited: 4 USED (low confidence) X. W. Zhou, J. J. Chavez, and D. Zubia, “Molecular Dynamics Analysis of Nanostructures.” 2016. link Times cited: 0 USED (low confidence) A. Kelley, “Comparison of three empirical force fields for phonon calculations in CdSe quantum dots.,” The Journal of chemical physics. 2016. link Times cited: 11 Abstract: Three empirical interatomic force fields are parametrized us… read more USED (low confidence) X. W. Zhou, M. E. Foster, R. Jones, P. Yang, H. Fan, and F. Doty, “A modified Stillinger-Weber potential for TlBr and its polymorphic extension,” Journal of Materials Science Research. 2015. link Times cited: 6 Abstract: TlBr is promising for g- and x- radiation detection, but suf… read more USED (low confidence) Y. Wu, R.-B. Li, J. Xiao, and Y. Jiang, “Crystallization in Supercooled BCC-Vanadium, HCP-Zinc and FCC-Aluminum.” 2015. link Times cited: 0 USED (low confidence) J. Farrell and D. Wales, “Clusters of coarse-grained water molecules.,” The journal of physical chemistry. A. 2014. link Times cited: 4 Abstract: Global optimization for molecular clusters can be significan… read more USED (low confidence) D. Nath and R. Das, “Experimental (XRD) and theoretical (DFT) analysis for understanding the influence of SHI irradiation on the stacking fault energy in CdSe nanocrystals,” Journal of Alloys and Compounds. 2021. link Times cited: 4 USED (low confidence) R. Jones, C. Weinberger, S. Coleman, and G. Tucker, “Introduction to Atomistic Simulation Methods.” 2016. link Times cited: 1 NOT USED (high confidence) D. Jasrasaria and E. Rabani, “Interplay of Surface and Interior Modes in Exciton-Phonon Coupling at the Nanoscale.,” Nano letters. 2021. link Times cited: 6 Abstract: Exciton-phonon coupling (EXPC) plays a key role in the optoe… read more NOT USED (high confidence) E. Chowdhury, M. Rahman, R. Jayan, and M. M. Islam, “Atomistic investigation on the mechanical properties and failure behavior of zinc-blende cadmium selenide (CdSe) nanowire,” Computational Materials Science. 2021. link Times cited: 2 NOT USED (high confidence) C. Chen et al., “Vacancy-assisted core transformation and mobility modulation of a-type edge dislocations in wurtzite GaN,” Journal of Physics D: Applied Physics. 2019. link Times cited: 3 Abstract: In this study, core structure dependent dislocation dynamics… read more NOT USED (high confidence) H. Hieu et al., “Structural and Thermomechanical Properties of Zincblende-Type ZnX (X = S, Se, Te),” Journal of Electronic Materials. 2019. link Times cited: 1 NOT USED (high confidence) M. Vohra, A. Nobakht, S. Shin, and S. Mahadevan, “Uncertainty quantification in non-equilibrium molecular dynamics simulations of thermal transport,” International Journal of Heat and Mass Transfer. 2018. link Times cited: 14 NOT USED (high confidence) M. Wen, S. Shirodkar, P. Plecháč, E. Kaxiras, R. Elliott, and E. Tadmor, “A force-matching Stillinger-Weber potential for MoS2: Parameterization and Fisher information theory based sensitivity analysis,” Journal of Applied Physics. 2017. link Times cited: 25 Abstract: Two-dimensional molybdenum disulfide (MoS2) is a promising m… read more NOT USED (high confidence) X. W. Zhou, R. Jones, and K. Chu, “Polymorphic improvement of Stillinger-Weber potential for InGaN,” Journal of Applied Physics. 2017. link Times cited: 4 Abstract: A Stillinger-Weber potential is computationally very efficie… read more NOT USED (high confidence) A. Takahashi, A. Seko, and I. Tanaka, “Linearized machine-learning interatomic potentials for non-magnetic elemental metals: Limitation of pairwise descriptors and trend of predictive power.,” The Journal of chemical physics. 2017. link Times cited: 20 Abstract: Machine-learning interatomic potential (MLIP) has been of gr… read more NOT USED (high confidence) X. W. Zhou and R. Jones, “A Stillinger-Weber Potential for InGaN,” Journal of Materials Science Research. 2017. link Times cited: 9 Abstract: Reducing defects in InGaN films deposited on GaN substrates … read more NOT USED (high confidence) X. W. Zhou, R. Jones, and J. Gruber, “Molecular dynamics simulations of substitutional diffusion,” Computational Materials Science. 2017. link Times cited: 23 NOT USED (high confidence) E. Voyiatzis and M. Böhm, “Atomic and global mechanical properties of systems described by the Stillinger–Weber potential,” Journal of Physics: Condensed Matter. 2016. link Times cited: 0 Abstract: Analytical expressions for the stress and elasticity tensors… read more NOT USED (high confidence) X. W. Zhou et al., “An atomistically validated continuum model for strain relaxation and misfit dislocation formation,” Journal of The Mechanics and Physics of Solids. 2016. link Times cited: 21 NOT USED (high confidence) S. Schreyeck et al., “Kinetic limitation of chemical ordering in Bi2Te3−xSex layers grown by molecular beam epitaxy,” Journal of Physics: Condensed Matter. 2016. link Times cited: 4 Abstract: We study the chemical ordering in Bi2Te3−xSex grown by molec… read more NOT USED (high confidence) Z. Fan, “Molecular Simulations of Nanoscale Transformations in Ionic Semiconductor Nanocrystals.” 2016. link Times cited: 0 Abstract: The aim of the study described in this thesis is to obtain a… read more NOT USED (high confidence) F. van Swol, X. W. Zhou, S. R. Challa, and J. E. Martin, “Thermodynamic properties of model CdTe/CdSe mixtures,” Molecular Simulation. 2016. link Times cited: 3 Abstract: We report on the thermodynamic properties of binary compound… read more NOT USED (high confidence) W.-T. Xu, L. Zhu, Y. Cai, G. Zhang, and B. Li, “Direction dependent thermal conductivity of monolayer phosphorene: parameterization of Stillinger-Weber potential and molecular dynamics study,” arXiv: Mesoscale and Nanoscale Physics. 2015. link Times cited: 70 Abstract: A Stillinger-Weber interatomic potential is parameterized fo… read more NOT USED (high confidence) B. Bonef et al., “Atomic arrangement at ZnTe/CdSe interfaces determined by high resolution scanning transmission electron microscopy and atom probe tomography,” Applied Physics Letters. 2015. link Times cited: 15 Abstract: High resolution scanning transmission electron microscopy an… read more NOT USED (high confidence) X. Zhou, M. E. Foster, F. Swol, J. E. Martin, and B. M. Wong, “Analytical Bond-Order Potential for the Cd–Te–Se Ternary System,” Journal of Physical Chemistry C. 2014. link Times cited: 13 NOT USED (high confidence) X. W. Zhou, J. J. Chavez, J. Cruz-Campa, and D. Zubia, “Towards model-guided defect reduction in Cd1−xZnxTe/CdS solar cells: Development of molecular dynamics models,” 2014 IEEE 40th Photovoltaic Specialist Conference (PVSC). 2014. link Times cited: 0 Abstract: Cd1-xZnxTe/CdS solar cells are currently limited by material… read more NOT USED (high confidence) X. Hu, R. Ciaglia, F. Pietrucci, G. A. Gallet, and W. Andreoni, “DFT-derived reactive potentials for the simulation of activated processes: the case of CdTe and CdTe:S.,” The journal of physical chemistry. B. 2014. link Times cited: 2 Abstract: We introduce a new ab initio derived reactive potential for … read more |
| Funding | Not available |
| Short KIM ID
The unique KIM identifier code.
| MO_503261197030_003 |
| Extended KIM ID
The long form of the KIM ID including a human readable prefix (100 characters max), two underscores, and the Short KIM ID. Extended KIM IDs can only contain alpha-numeric characters (letters and digits) and underscores and must begin with a letter.
| SW_ZhouWardMartin_2013_CdTeZnSeHgS__MO_503261197030_003 |
| DOI |
10.25950/8846e83d https://doi.org/10.25950/8846e83d https://commons.datacite.org/doi.org/10.25950/8846e83d |
| KIM Item Type
Specifies whether this is a Portable Model (software implementation of an interatomic model); Portable Model with parameter file (parameter file to be read in by a Model Driver); Model Driver (software implementation of an interatomic model that reads in parameters).
| Portable Model using Model Driver SW__MD_335816936951_005 |
| Driver | SW__MD_335816936951_005 |
| KIM API Version | 2.0 |
| Potential Type | sw |
| Previous Version | SW_ZhouWardMartin_2013_CdTeZnSeHgS__MO_503261197030_002 |
| Grade | Name | Category | Brief Description | Full Results | Aux File(s) |
|---|---|---|---|---|---|
| P | vc-species-supported-as-stated | mandatory | The model supports all species it claims to support; see full description. |
Results | Files |
| P | vc-periodicity-support | mandatory | Periodic boundary conditions are handled correctly; see full description. |
Results | Files |
| P | vc-permutation-symmetry | mandatory | Total energy and forces are unchanged when swapping atoms of the same species; see full description. |
Results | Files |
| A | vc-forces-numerical-derivative | consistency | Forces computed by the model agree with numerical derivatives of the energy; see full description. |
Results | Files |
| P | vc-dimer-continuity-c1 | informational | The energy versus separation relation of a pair of atoms is C1 continuous (i.e. the function and its first derivative are continuous); see full description. |
Results | Files |
| P | vc-objectivity | informational | Total energy is unchanged and forces transform correctly under rigid-body translation and rotation; see full description. |
Results | Files |
| P | vc-inversion-symmetry | informational | Total energy is unchanged and forces change sign when inverting a configuration through the origin; see full description. |
Results | Files |
| P | vc-memory-leak | informational | The model code does not have memory leaks (i.e. it releases all allocated memory at the end); see full description. |
Results | Files |
| P | vc-thread-safe | mandatory | The model returns the same energy and forces when computed in serial and when using parallel threads for a set of configurations. Note that this is not a guarantee of thread safety; see full description. |
Results | Files |
| P | vc-unit-conversion | mandatory | The model is able to correctly convert its energy and/or forces to different unit sets; see full description. |
Results | Files |
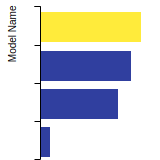
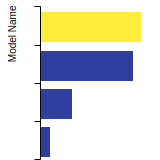
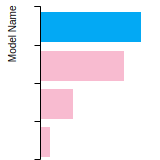
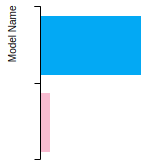
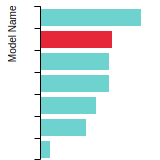
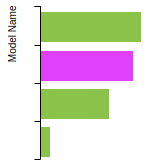
BCC Lattice Constant
This bar chart plot shows the mono-atomic body-centered cubic (bcc) lattice constant predicted by the current model (shown in the unique color) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
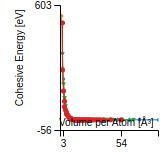
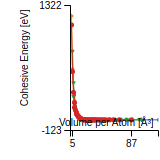
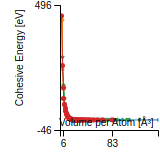
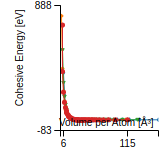
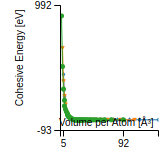
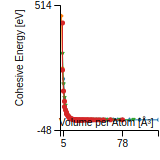
Cohesive Energy Graph
This graph shows the cohesive energy versus volume-per-atom for the current mode for four mono-atomic cubic phases (body-centered cubic (bcc), face-centered cubic (fcc), simple cubic (sc), and diamond). The curve with the lowest minimum is the ground state of the crystal if stable. (The crystal structure is enforced in these calculations, so the phase may not be stable.) Graphs are generated for each species supported by the model.
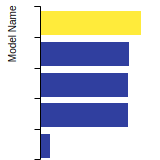
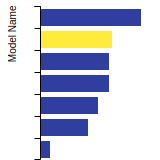
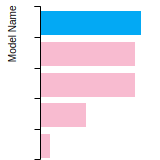
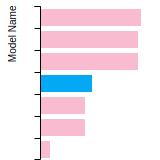
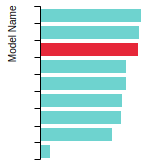
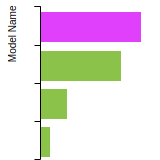
Diamond Lattice Constant
This bar chart plot shows the mono-atomic face-centered diamond lattice constant predicted by the current model (shown in the unique color) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
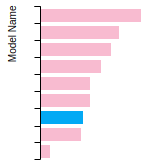
Dislocation Core Energies
This graph shows the dislocation core energy of a cubic crystal at zero temperature and pressure for a specific set of dislocation core cutoff radii. After obtaining the total energy of the system from conjugate gradient minimizations, non-singular, isotropic and anisotropic elasticity are applied to obtain the dislocation core energy for each of these supercells with different dipole distances. Graphs are generated for each species supported by the model.
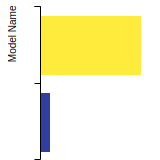
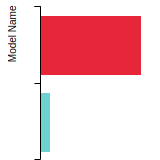
(No matching species)FCC Elastic Constants
This bar chart plot shows the mono-atomic face-centered cubic (fcc) elastic constants predicted by the current model (shown in blue) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
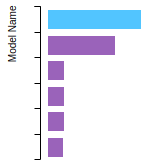
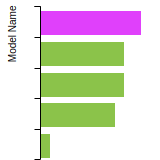
FCC Lattice Constant
This bar chart plot shows the mono-atomic face-centered cubic (fcc) lattice constant predicted by the current model (shown in red) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
FCC Stacking Fault Energies
This bar chart plot shows the intrinsic and extrinsic stacking fault energies as well as the unstable stacking and unstable twinning energies for face-centered cubic (fcc) predicted by the current model (shown in blue) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
(No matching species)FCC Surface Energies
This bar chart plot shows the mono-atomic face-centered cubic (fcc) relaxed surface energies predicted by the current model (shown in blue) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
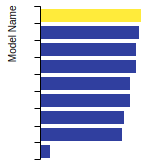
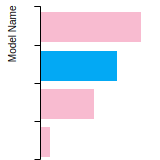
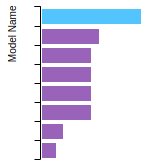
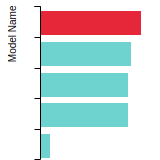
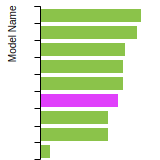
(No matching species)SC Lattice Constant
This bar chart plot shows the mono-atomic simple cubic (sc) lattice constant predicted by the current model (shown in the unique color) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
Cubic Crystal Basic Properties Table
Species: CdSpecies: Hg
Species: S
Species: Se
Species: Te
Species: Zn
Creators:
Contributor: karls
Publication Year: 2019
DOI: https://doi.org/10.25950/64cb38c5
This Test Driver uses LAMMPS to compute the cohesive energy of a given monoatomic cubic lattice (fcc, bcc, sc, or diamond) at a variety of lattice spacings. The lattice spacings range from a_min (=a_min_frac*a_0) to a_max (=a_max_frac*a_0) where a_0, a_min_frac, and a_max_frac are read from stdin (a_0 is typically approximately equal to the equilibrium lattice constant). The precise scaling and number of lattice spacings sampled between a_min and a_0 (a_0 and a_max) is specified by two additional parameters passed from stdin: N_lower and samplespacing_lower (N_upper and samplespacing_upper). Please see README.txt for further details.
Creators:
Contributor: ilia
Publication Year: 2024
DOI: https://doi.org/10.25950/888f9943
Computes the elastic constants for an arbitrary crystal. A robust computational protocol is used, attempting multiple methods and step sizes to achieve an acceptably low error in numerical differentiation and deviation from material symmetry. The crystal structure is specified using the AFLOW prototype designation as part of the Crystal Genome testing framework. In addition, the distance from the obtained elasticity tensor to the nearest isotropic tensor is computed.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Elastic constants for SeZn in AFLOW crystal prototype A2B_cP12_205_c_a at zero temperature and pressure v000 | view | 115444 | |
| Elastic constants for SZn in AFLOW crystal prototype A2B_cP12_205_c_a at zero temperature and pressure v000 | view | 152247 |
Creators: Junhao Li and Ellad Tadmor
Contributor: tadmor
Publication Year: 2019
DOI: https://doi.org/10.25950/5853fb8f
Computes the cubic elastic constants for some common crystal types (fcc, bcc, sc, diamond) by calculating the hessian of the energy density with respect to strain. An estimate of the error associated with the numerical differentiation performed is reported.
Creators:
Contributor: ilia
Publication Year: 2024
DOI: https://doi.org/10.25950/2f2c4ad3
Computes the equilibrium crystal structure and energy for an arbitrary crystal at zero temperature and applied stress by performing symmetry-constrained relaxation. The crystal structure is specified using the AFLOW prototype designation. Multiple sets of free parameters corresponding to the crystal prototype may be specified as initial guesses for structure optimization. No guarantee is made regarding the stability of computed equilibria, nor that any are the ground state.
Creators:
Contributor: ilia
Publication Year: 2025
DOI: https://doi.org/10.25950/866c7cfa
Computes the equilibrium crystal structure and energy for an arbitrary crystal at zero temperature and applied stress by performing symmetry-constrained relaxation. The crystal structure is specified using the AFLOW prototype designation. Multiple sets of free parameters corresponding to the crystal prototype may be specified as initial guesses for structure optimization. No guarantee is made regarding the stability of computed equilibria, nor that any are the ground state.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Equilibrium crystal structure and energy for Cd in AFLOW crystal prototype A_hP2_194_c v003 | view | 150867 | |
| Equilibrium crystal structure and energy for Zn in AFLOW crystal prototype A_hP2_194_c v003 | view | 166239 | |
| Equilibrium crystal structure and energy for Hg in AFLOW crystal prototype A_hP3_191_ad v003 | view | 144366 | |
| Equilibrium crystal structure and energy for Hg in AFLOW crystal prototype A_tI2_139_a v003 | view | 163080 |
Creators: Daniel S. Karls and Junhao Li
Contributor: karls
Publication Year: 2019
DOI: https://doi.org/10.25950/2765e3bf
Equilibrium lattice constant and cohesive energy of a cubic lattice at zero temperature and pressure.
Creators: Daniel S. Karls and Junhao Li
Contributor: karls
Publication Year: 2019
DOI: https://doi.org/10.25950/c339ca32
Calculates lattice constant of hexagonal bulk structures at zero temperature and pressure by using simplex minimization to minimize the potential energy.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Equilibrium lattice constants for hcp Cd v005 | view | 19672 | |
| Equilibrium lattice constants for hcp Hg v005 | view | 19985 | |
| Equilibrium lattice constants for hcp S v005 | view | 23087 | |
| Equilibrium lattice constants for hcp Se v005 | view | 21959 | |
| Equilibrium lattice constants for hcp Te v005 | view | 23650 | |
| Equilibrium lattice constants for hcp Zn v005 | view | 19014 |
Creators:
Contributor: efuem
Publication Year: 2023
DOI: https://doi.org/10.25950/fca89cea
Computes the monovacancy formation energy and relaxation volume for cubic and hcp monoatomic crystals.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Monovacancy formation energy and relaxation volume for hcp Cd | view | 282703 | |
| Monovacancy formation energy and relaxation volume for hcp Zn | view | 374949 |
Creators:
Contributor: efuem
Publication Year: 2023
DOI: https://doi.org/10.25950/c27ba3cd
Computes the monovacancy formation and migration energies for cubic and hcp monoatomic crystals.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Vacancy formation and migration energy for hcp Cd | view | 3701712 | |
| Vacancy formation and migration energy for hcp Zn | view | 3023079 |
| Test | Error Categories | Link to Error page |
|---|---|---|
| Cohesive energy versus lattice constant curve for bcc Se v004 | other | view |
ElasticConstantsHexagonal__TD_612503193866_004
| Test | Error Categories | Link to Error page |
|---|---|---|
| Elastic constants for hcp Cd at zero temperature v004 | other | view |
| Elastic constants for hcp Hg at zero temperature v004 | other | view |
| Elastic constants for hcp S at zero temperature v004 | other | view |
| Elastic constants for hcp Se at zero temperature v004 | other | view |
| Elastic constants for hcp Te at zero temperature v004 | other | view |
| Elastic constants for hcp Zn at zero temperature v004 | other | view |
EquilibriumCrystalStructure__TD_457028483760_000
EquilibriumCrystalStructure__TD_457028483760_002
EquilibriumCrystalStructure__TD_457028483760_003
| Test | Error Categories | Link to Error page |
|---|---|---|
| Equilibrium crystal structure and energy for Hg in AFLOW crystal prototype A_mC2_12_a v003 | other | view |
| Equilibrium crystal structure and energy for Hg in AFLOW crystal prototype A_mC6_12_ai v003 | other | view |
| SW_ZhouWardMartin_2013_CdTeZnSeHgS__MO_503261197030_003.txz | Tar+XZ | Linux and OS X archive |
| SW_ZhouWardMartin_2013_CdTeZnSeHgS__MO_503261197030_003.zip | Zip | Windows archive |
This Model requires a Model Driver. Archives for the Model Driver SW__MD_335816936951_005 appear below.
| SW__MD_335816936951_005.txz | Tar+XZ | Linux and OS X archive |
| SW__MD_335816936951_005.zip | Zip | Windows archive |