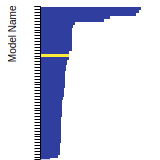
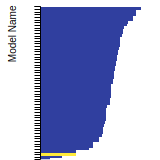
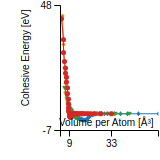
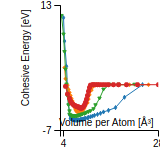
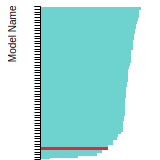
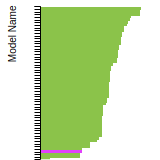
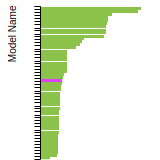
Test
Test Results
Link to Test Results page
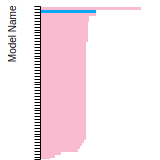
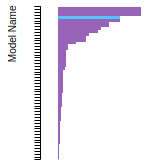
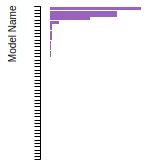
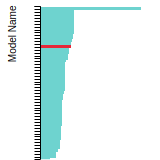
Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2335
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2335
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2911
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2719
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2335
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2815
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2207
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2335
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2335
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2943
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2303
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
3007
Conjugate gradient relaxation of random finite cluster of Si atoms v003
3007
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2911
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2719
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2751
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2751
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2687
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2687
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2719
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2847
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2687
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2207
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2719
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2175
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2687
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2719
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2239
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2335
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2719
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2303
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2175
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2911
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2687
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2751
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2783
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2719
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2751
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2207
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2687
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2879
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2335
Conjugate gradient relaxation of random finite cluster of Si atoms v003
1951
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2207
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2815
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2751
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2719
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2687
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2783
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2335
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2751
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2207
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2207
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2271
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2751
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2783
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2335
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2271
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2719
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2335
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2079
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2271
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2719
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2239
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2719
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2815
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2175
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2335
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2815
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2207
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2751
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2335
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2687
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2079
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2687
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2303
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2719
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2783
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2911
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2975
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2335
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2303
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2079
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2111
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2335
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2207
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2335
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2719
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2687
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2271
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2719
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2303
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2815
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2751
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2239
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2335
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2687
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2303
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2175
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2879
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2687
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2719
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
1983
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2719
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2271
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2751
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2303
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2687
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2303
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2943
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2719
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2751
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2239
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2303
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2719
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2687
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2911
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2783
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2335
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2303
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2687
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2783
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2335
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2303
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2271
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2111
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2271
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2047
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2879
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2303
Conjugate gradient relaxation of random finite cluster of Si atoms v003
3071
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2815
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2815
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2687
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2271
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2271
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
1983
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2719
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2271
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2175
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2751
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2751
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2239
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2239
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2687
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2239
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2911
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2143
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2783
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2239
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
1951
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2719
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2111
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2687
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2303
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2303
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2175
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2143
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2847
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2335
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2335
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2303
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2719
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2719
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2175
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2335
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2271
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2719
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2175
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2239
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2143
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2687
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2175
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2751
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2751
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2303
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2751
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2175
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2335
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2303
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2303
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2335
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2175
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2079
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2815
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2751
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2335
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2783
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2719
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2687
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2687
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2111
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2911
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2239
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2751
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2303
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2687
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2143
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2303
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2815
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2111
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2303
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2751
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2271
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2271
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2719
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2687
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2111
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2751
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2271
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2303
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2719
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2335
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2815
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2719
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2687
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2943
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2751
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2303
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2303
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2751
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2335
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2719
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2271
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2751
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2815
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2687
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2431
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2847
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2783
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2207
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2303
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2815
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2271
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2335
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2783
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2143
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2527
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2303
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2239
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2463
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2559
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2495
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2591
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2623
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2367
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2399
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2655
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2303
Conjugate gradient relaxation of random finite cluster of Si atoms v003
2335