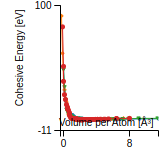
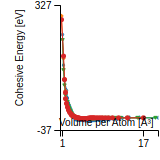
Citations
This panel presents information regarding the papers that have cited the interatomic potential (IP) whose page you are on.
The OpenKIM machine learning based Deep Citation framework is used to determine whether the citing article actually used the IP in computations (denoted by "USED") or only provides it as a background citation (denoted by "NOT USED"). For more details on Deep Citation and how to work with this panel, click the documentation link at the top of the panel.
The word cloud to the right is generated from the abstracts of IP principle source(s) (given below in "How to Cite") and the citing articles that were determined to have used the IP in order to provide users with a quick sense of the types of physical phenomena to which this IP is applied.
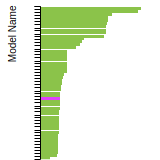
The bar chart shows the number of articles that cited the IP per year. Each bar is divided into green (articles that USED the IP) and blue (articles that did NOT USE the IP).
Users are encouraged to correct Deep Citation errors in determination by clicking the speech icon next to a citing article and providing updated information. This will be integrated into the next Deep Citation learning cycle, which occurs on a regular basis.
OpenKIM acknowledges the support of the Allen Institute for AI through the Semantic Scholar project for providing citation information and full text of articles when available, which are used to train the Deep Citation ML algorithm.
|
This panel provides information on past usage of this interatomic potential (IP) powered by the OpenKIM Deep Citation framework. The word cloud indicates typical applications of the potential. The bar chart shows citations per year of this IP (bars are divided into articles that used the IP (green) and those that did not (blue)). The complete list of articles that cited this IP is provided below along with the Deep Citation determination on usage. See the Deep Citation documentation for more information.

351 Citations (229 used)
Help us to determine which of the papers that cite this potential actually used it to perform calculations. If you know, click the .
USED (high confidence) S. Wang, H. Feng, and Z. Guo, “Stacking and thickness effects on cross-plane thermal conductivity of hexagonal boron nitride,” Computational Materials Science. 2023. link Times cited: 0 USED (high confidence) T. Huang et al., “Self-Modifying Nanointerface Driving Ultrahigh Bidirectional Thermal Conductivity Boron Nitride-Based Composite Flexible Films,” Nano-Micro Letters. 2022. link Times cited: 9 USED (high confidence) Y. Liu et al., “A Qualitative Study of the Disorder Effect on the Phonon Transport in a Two-Dimensional Graphene/h-BN Heterostructure,” Frontiers in Materials. 2022. link Times cited: 5 Abstract: Recently, massive efforts have been made to control phonon t… read moreAbstract: Recently, massive efforts have been made to control phonon transport via introducing disorder. Meanwhile, materials informatics, an advanced material-discovery technology that combines data-driven search algorithms and material property simulations, has made significant progress and shown accurate prediction ability in studying the target properties of new materials. However, with the introduction of disorder, the design space of random structures is greatly expanded. Global optimization for the entire domain is nearly impossible with the current computer resource even when materials informatics reduces the design space to a few percent. Toward the goal of reducing design space, we investigate the effect of different types of disorders on phonon transport in two-dimensional graphene/hexagonal boron nitride heterostructure using non-equilibrium molecular dynamics simulation. The simulation results show that when the hexagonal boron nitride is distributed disorderly in the coherent phonon-dominated structure, that is, the structure with a period length of 1.23 nm, the thermal conductivity is significantly reduced due to the appearance of coherent phonon localization. By qualitatively analyzing different types of disorder, we found that the introduction of disordered structure in the cross direction with a larger shift distance can further reduce the thermal conductivity. Further physical mechanism analysis revealed that the structures with lower thermal conductivity were caused by weak propagation and strong localization of phonon. Our findings have implications for accelerating machine learning in the search for structures with the lowest thermal conductivity, and provide some guidance for the future synthesis of 2D heterostructures with unique thermal properties. read less USED (high confidence) V.-T. Pham and T. Fang, “Mechanical and thermal characterizations of nanoporous two-dimensional boron nitride membranes,” Scientific Reports. 2022. link Times cited: 7 USED (high confidence) J. S. Lima, I. S. Oliveira, S. Azevedo, A. Freitas, C. Bezerra, and L. Machado, “Mechanical and electronic properties of boron nitride nanosheets with graphene domains under strain,” RSC Advances. 2021. link Times cited: 1 Abstract: Hybrid structures comprised of graphene domains embedded in … read moreAbstract: Hybrid structures comprised of graphene domains embedded in larger hexagonal boron nitride (h-BN) nanosheets were first synthesized in 2013. However, the existing theoretical investigations on them have only considered relaxed structures. In this work, we use Density Functional Theory (DFT) and Molecular Dynamics (MD) simulations to investigate the mechanical and electronic properties of this type of nanosheet under strain. Our results reveal that the Young's modulus of the hybrid sheets depends only on the relative concentration of graphene and h-BN in the structure, showing little dependence on the shape of the domain or the size of the structure for a given concentration. Regarding the tensile strength, we obtained higher values using triangular graphene domains. We find that the studied systems can withstand large strain values (between 15% and 22%) before fracture, which always begins at the weaker C–B bonds located at the interface between the two materials. Concerning the electronic properties, we find that by combining composition and strain, we can produce hybrid sheets with band gaps spanning an extensive range of values (between 1.0 eV and 3.5 eV). Our results also show that the band gap depends more on the composition than on the external strain, particularly for structures with low carbon concentration. The combination of atomic-scale thickness, high ultimate strain, and adjustable band gap suggests applications of h-BN nanosheets with graphene domains in wearable electronics. read less USED (high confidence) B. Chava, Y. Wang, and S. Das, “Boron Nitride Nanotube–Salt–Water Hybrid: Toward Zero-Dimensional Liquid Water and Highly Trapped Immobile Single Anions Inside One-Dimensional Nanostructures,” Journal of Physical Chemistry C. 2021. link Times cited: 3 USED (high confidence) B. Mortazavi, “Ultrahigh thermal conductivity and strength in direct-gap semiconducting graphene-like BC6N: A first-principles and classical investigation.” 2021. link Times cited: 35 USED (high confidence) L. Razzaghi, F. Khoeini, A. Rajabpour, and M. Khalkhali, “Thermal transport in two-dimensional C3N/C2N superlattices: A molecular dynamics approach.” 2021. link Times cited: 12 USED (high confidence) I. S. Oliveira, J. S. Lima, A. Freitas, C. G. Bezerra, S. Azevedo, and L. D. Machado, “Investigating size effects in graphene–BN hybrid monolayers: a combined density functional theory-molecular dynamics study,” RSC Advances. 2021. link Times cited: 1 Abstract: We combine Density Functional Theory (DFT) and classical Mol… read moreAbstract: We combine Density Functional Theory (DFT) and classical Molecular Dynamics (MD) simulations to study graphene–boron nitride (BN) hybrid monolayers spanning a wide range of sizes (from 2 nm to 100 nm). Our simulations show that the elastic properties depend on the fraction of BN contained in the monolayer, with Young's modulus values decreasing as the BN concentration increases. Furthermore, our calculations reveal that the mechanical properties are weakly anisotropic. We also analyze the evolution of the stress distribution during our MD simulations. Curiously, we find that stress does not concentrate on the graphene–BN interface, even though fracture always starts in this region. Hence, we find that fracture is caused by the lower strength of C–N and C–B bonds, rather than by high local stress values. Still, in spite of the fact that the weaker bonds in the interface region become a lower fraction of the total as size increases, we find that the mechanical properties of the hybrid monolayers do not depend on the size of the structure, for constant graphene/BN concentrations. Our results indicate that the mechanical properties of the hybrid monolayers are independent of scale, so long as the graphene sheet and the h-BN nanodomain decrease or increase proportionately. read less USED (high confidence) O. Farzadian, C. Spitas, and K. Kostas, “Graphene-carbon nitride interface-geometry effects on thermal rectification: a molecular dynamics simulation,” Nanotechnology. 2021. link Times cited: 14 Abstract: In this paper we expand our previous study on phonon thermal… read moreAbstract: In this paper we expand our previous study on phonon thermal rectification (TR) exhibited in a hybrid graphene-carbon nitride system (G−C3N) to investigate the system’s behavior under a wider range of temperature differences, between the two employed baths, and the effects of media-interface geometry on the rectification factor. Our simulation results reveal a sigmoid relation between TR and temperature difference, with a sample-size depending upper asymptote occurring at generally large temperature differences. The achieved TR values are significant and go up to around 120% for ΔT = 150 K. Furthermore, the consideration of varying media-interface geometries yields a non-negligible effect on TR and highlights areas for further investigation. Finally, calculations of Kapitza resistance at the G-C3N interface are performed for assisting us in the understanding of interface-geometry effects on TR. read less USED (high confidence) L. Patra, G. Mallick, G. Sachdeva, C. J. Shock, and R. Pandey, “Orientation-dependent mechanical response of graphene/BN hybrid nanostructures,” Nanotechnology. 2021. link Times cited: 6 Abstract: Graphene-based hybrid van der Waals structures have emerged … read moreAbstract: Graphene-based hybrid van der Waals structures have emerged as a new class of materials for novel multifunctional applications. In such a vertically-stacked heterostructure, it is expected that its mechanical strength can be tailored by the orientation of the constituent monolayers relative to each other. In this paper, we explore this hypothesis by investigating the orientation dependence of the mechanical properties of graphene/h-BN heterostructures together with that of graphene and h-BN bilayers. The calculated results simulating the pull-out experiment show a noticeable dependence of the (out-of-plane) transverse mechanical response, which is primarily governed by the interlayer strength, on the stacking configurations. The degree of the dependence is directly related to the nature of the interlayer interactions, which change from covalent to covalent polar in going from graphene bilayer to graphene/BN to BN bilayer. In contrast, molecular dynamics simulations mimicking nanoindentation experiments predict that the in-plane mechanical response, which mainly depends on the intra-layer interactions, shows little or no dependence on the stacking-order. The BN monolayer is predicted to fracture before graphene regardless of the stacking pattern or configuration in the graphene/BN heterostructure, affirming the mechanical robustness of graphene. Thus, the graphene-based hybrid structures retain both stiffness and toughness required for a wide range of optoelectromechanical applications. read less USED (high confidence) W. Su, C. Zhu, A. Hua, S. Li, and J. Zhao, “Fracture behavior dependent on crack-tip shapes in nanoscale crack-defect monolayer boron nitride sheets,” International Journal of Smart and Nano Materials. 2021. link Times cited: 3 Abstract: ABSTRACT Nanoscale defects, including cracks, circular holes… read moreAbstract: ABSTRACT Nanoscale defects, including cracks, circular holes, and the triangular-shaped defects, often occur in the growth of boron nitride nanosheets (BNNS). In this study, the fracture behavior of chiral BNNS with different crack-tip shapes and the interactions of nanoscale crack-defects are studied using molecular dynamics (MD) simulations and finite element (FE) analysis. Both MD and FE results indicate that the fracture strength of BNNS with two crack tips (t = 2) is significantly higher than that with one crack tip (t = 1), in which the difference in zigzag (ZZ) direction is more obvious than that in armchair (AC) direction, mainly due to the fact that the change of bond angles near the crack tips is more substantial in the ZZ direction than those in the AC direction. Our results show that the fracture strength of BNNS strongly depends on crack-tip shapes, chiral angles, the defect-to-crack tip spacing and deflection angles. Checking against the current MD simulations and FE analysis shows the present results are reasonable. This study should be of great importance for enhancing the fracture performance of BNNS by modulating their crack-tip shapes and the interactions of nanoscale crack-defects. Graphical abstract read less USED (high confidence) L. Kiani, J. Hasanzadeh, and F. Yousefi, “Phonon modes contribution in thermal rectification in graphene-C3B junction: A molecular dynamics study,” Physica E: Low-dimensional Systems and Nanostructures. 2020. link Times cited: 6 USED (high confidence) Y. Wang, Y. Guo, and W. Guo, “Screening effect of monolayer van der Waals crystals on surface deicing: a molecular simulation study.,” Physical chemistry chemical physics : PCCP. 2020. link Times cited: 4 Abstract: Our extensive molecular dynamics simulations reveal a signif… read moreAbstract: Our extensive molecular dynamics simulations reveal a significant screening effect of monolayer graphene and hexagonal boron nitride (h-BN) on surface deicing of substrates with different degrees of hydrophilicity, including superhydrophilic (SHP) and superhydrophobic (SHB) substrates. Compared with bare surfaces, graphene and h-BN reduce the interfacial shear strength and the normal detaching strength of ice on an SHP substrate but increase the shear and detaching strengths on hydrophobic and SHB substrates. However, the shear and detaching strengths of ice become approximately unified on all of the surfaces, when interface ice layers melt into liquid water, demonstrating the screening capability from graphene and h-BN that weakens the influence of substrates on ice adhesion. Graphene and h-BN coatings suppress ice premelting on the SHP surface and change the dielectric constant of interface ice or water. This work could deepen our understanding of the role of van der Waals crystals in deicing coating. read less USED (high confidence) T. C. Sagar and V. Chinthapenta, “Effect of substitutional and vacancy defects on the electrical and mechanical properties of 2D-hexagonal boron nitride,” Journal of Molecular Modeling. 2020. link Times cited: 5 USED (high confidence) T. Liang, M. Zhou, P. Zhang, P. Yuan, and D. Yang, “Multilayer in-plane graphene/hexagonal boron nitride heterostructures: Insights into the interfacial thermal transport properties,” International Journal of Heat and Mass Transfer. 2020. link Times cited: 74 USED (high confidence) I. M. Felix and L. Pereira, “Suppression of coherent thermal transport in quasiperiodic graphene-hBN superlattice ribbons,” Carbon. 2020. link Times cited: 27 USED (high confidence) A. Galashev, K. Ivanichkina, K. Katin, and M. Maslov, “Computational Study of Lithium Intercalation in Silicene Channels on a Carbon Substrate after Nuclear Transmutation Doping,” Comput. 2019. link Times cited: 10 Abstract: Silicene is considered to be the most promising anode materi… read moreAbstract: Silicene is considered to be the most promising anode material for lithium-ion batteries. In this work, we show that transmutation doping makes silicene substantially more suitable for use as an anode material. Pristine and modified bilayer silicene was simulated on a graphite substrate using the classical molecular dynamics method. The parameters of Morse potentials for alloying elements were determined using quantum mechanical calculations. The main advantage of modified silicene is its low deformability during lithium intercalation and its possibility of obtaining a significantly higher battery charge capacity. Horizontal and vertical profiles of the density of lithium as well as distributions of the most significant stresses in the walls of the channels were calculated both in undoped and doped systems with different gaps in silicene channels. The energies of lithium adsorption on silicene, including phosphorus-doped silicene, were determined. High values of the self-diffusion coefficient of lithium atoms in the silicene channels were obtained, which ensured a high cycling rate. The calculations showed that such doping increased the normal stress on the walls of the channel filled with lithium to 67% but did not provoke a loss of mechanical strength. In addition, doping achieved a greater battery capacity and higher charging/discharging rates. read less USED (high confidence) X. Zhou et al., “Kinking effects and transport properties of coaxial BN-C nanotubes as revealed by in situ transmission electron microscopy and theoretical analysis,” APL Materials. 2019. link Times cited: 0 Abstract: The insights into transport behavior and the effects of bend… read moreAbstract: The insights into transport behavior and the effects of bending on heterostructures constructed from boron nitride (BN) and carbon (C) nanotubes are important for their flexible device applications because the two systems have equally excellent mechanical but completely different electrical properties. In this work, coaxial BN–C nanotubes have been fabricated and their intrinsic transport properties, as well as structural and electrical response to bending deformation, are studied inside a high-resolution transmission electron microscope. Ballistic, diffusive, and hopping transports within different tube length ranges have been observed. When bending deformation was applied to the tubes, although severe kinking becomes apparent, their transport properties are not notably affected. Meanwhile, both theoretical and experimental analyses confirm that the kink positions depend on the ratio of tube diameter to its length. Possible formation of quantum dots, directly within the kink areas, was predicted through calculations of electron density redistribution between nanotube walls at bending.The insights into transport behavior and the effects of bending on heterostructures constructed from boron nitride (BN) and carbon (C) nanotubes are important for their flexible device applications because the two systems have equally excellent mechanical but completely different electrical properties. In this work, coaxial BN–C nanotubes have been fabricated and their intrinsic transport properties, as well as structural and electrical response to bending deformation, are studied inside a high-resolution transmission electron microscope. Ballistic, diffusive, and hopping transports within different tube length ranges have been observed. When bending deformation was applied to the tubes, although severe kinking becomes apparent, their transport properties are not notably affected. Meanwhile, both theoretical and experimental analyses confirm that the kink positions depend on the ratio of tube diameter to its length. Possible formation of quantum dots, directly within the kink areas, was predicted through ... read less USED (high confidence) F. Liu et al., “Enhancement of thermal energy transport across the graphene/h-BN heterostructure interface.,” Nanoscale. 2019. link Times cited: 17 Abstract: Enhancing thermal energy transport is critical for the appli… read moreAbstract: Enhancing thermal energy transport is critical for the applications of 2-dimensional materials. Here, we explored the methods of enhancing the interfacial thermal energy transport across the graphene (GR)/hexagonal boron nitride (h-BN) heterostructure interface, and revealed the enhancement mechanisms of interfacial thermal energy transport by applying non-equilibrium molecular dynamics (NEMD) simulations. The computational results indicated that both doping and interface topography optimization could effectively improve the interfacial thermal conductance (ITC) of the GR/h-BN heterostructure. In particular, the enhancement of the zigzag interface topography led to a much better result than the other methods. Doping and interface topography optimization increased the overlap of the phonon density of states (PDOS). Temperature had a negligible effect on the ITC of the GR/h-BN heterostructure when the temperature exceeded 600 K. read less USED (high confidence) A. Rajabpour, S. Bazrafshan, and S. Volz, “Carbon-nitride 2D nanostructures: thermal conductivity and interfacial thermal conductance with the silica substrate.,” Physical chemistry chemical physics : PCCP. 2019. link Times cited: 36 Abstract: The rate of heat dissipation from a 2D nanostructure strongl… read moreAbstract: The rate of heat dissipation from a 2D nanostructure strongly depends on the interfacial thermal conductance with its substrate. In this paper, the interfacial thermal conductance of carbon-nitride 2D nanostructures (C3N, C2N, C3N4's) with silica substrates was investigated using transient molecular dynamics simulations. It was found that a 2D nanostructure with higher thermal conductivity, has a lower value of interfacial thermal conductance with the silica substrate. The thermal conductivity of suspended carbon-nitride 2D nanostructures was also calculated using the Green-Kubo formalism and compared with that of graphene as a reference structure. It was found that the thermal conductivities of C3N, C2N, C3N4 (s-triazine) and C3N4 (tri-triazine) are respectively 62%, 4%, 4% and 2% that of graphene; while their interfacial thermal conductances with silica are 113%, 171%, 212% and 188% that of graphene. These different behaviors of the thermal conductivity and the interfacial thermal conductance with the substrate may be important in the thermal management of carbon-nitride 2D nanostructures in nanoelectronics. read less USED (high confidence) S. Thomas and S. U. Lee, “Atomistic insights into the anisotropic mechanical properties and role of ripples on the thermal expansion of h-BCN monolayers,” RSC Advances. 2019. link Times cited: 27 Abstract: Monolayer boron–carbon–nitrogen (h-BCN) has been studied in … read moreAbstract: Monolayer boron–carbon–nitrogen (h-BCN) has been studied in comparison with graphene and hexagonal boron nitride (h-BN) using classical molecular dynamics (MD) simulations with an aim to better understand the structural and thermal behaviors and the anisotropic mechanical properties. The structural features of the simulated sample were analyzed using the pair-correlation function and a full width at half maximum (FWHM). As a hetero-structure of h-BN and graphene, the C–C bond in the h-BCN is responsible for an improved FWHM compared to graphene. Consistent with graphene and h-BN, the in-plane lattice parameter of h-BCN shows thermal contraction over a wide range of temperatures and exhibits a system size dependence. The observed thermal contraction is explained by the presence of out-of-plane bending modes excited at finite temperatures. A tensile test has been performed as a suitable means of measuring the mechanical properties of the h-BCN sheet for zigzag and armchair orientations and found that it is mechanically anisotropic and stable under various strain directions and temperatures. The fracture strength of h-BCN is affected by loading direction and temperature. We found that the Young's modulus of h-BCN is smaller than that of graphene but is higher than that of an h-BN monolayer, suggesting that h-BCN has high mechanical stiffness. Our modeling-based findings provide a guide for future experiments concerning the physical properties of this advanced composite material. read less USED (high confidence) D. Han et al., “Phonon thermal conduction in a graphene–C3N heterobilayer using molecular dynamics simulations,” Nanotechnology. 2018. link Times cited: 51 Abstract: Two-dimensional (2D) graphene (GRA) and polyaniline (C3N) mo… read moreAbstract: Two-dimensional (2D) graphene (GRA) and polyaniline (C3N) monolayers are attracting growing research interest due to their excellent electrical and thermal properties. In this work, in-plane and out-of-plane phonon thermal conduction of GRA–C3N heterobilayer are systematically investigated by using classical molecular dynamics simulations. Effects of system size, temperature and interlayer coupling strength on the in-plane thermal conductivity (k) and out-of-plane interfacial thermal resistance (R) are evaluated. Firstly, a monotonic increasing trend of k with increasing system size is observed, while a negative correlation between thermal conductivity and temperature is revealed. The interlayer coupling strength is found to have a weak effect on the in-plane thermal conductivity of the heterobilayer. Secondly, at T = 300 K and χ = 1, the predicted R of GRA → C3N and C3N → GRA are 1.29 × 10−7 K m2 W−1 and 1.35 × 10−7 K m2 W−1, respectively, which indicates that there is no significant thermal rectification phenomenon. It can also be observed that R decreases monotonically with increasing temperature and coupling strength due to the enhanced Umklapp phonon scattering and the phonon transmission probability across the interface. Phonon density of states, phonon dispersions and participation ratios are evaluated to reveal the mechanism of heat conduction in the heterobilayer. This work contributes the valuable thermal information to modulate the phonon behaviors in 2D heterobilayer based nanoelectronics. read less USED (high confidence) T. Jiang, Z. Wang, X. Ruan, and Y. Zhu, “Equi-biaxial compressive strain in graphene: Grüneisen parameter and buckling ridges,” 2D Materials. 2018. link Times cited: 19 Abstract: Strain and defects in graphene have critical impact on morph… read moreAbstract: Strain and defects in graphene have critical impact on morphology and properties of graphene. Here we report equi-biaxial compressive strain in monolayer graphene on SiO2 and Si3N4 substrates induced by thermal cycling in vacuum. The equi-biaxial strain is attributed to the mismatch in coefficient of thermal expansion between graphene and the substrate and sliding of graphene on the substrate. The sliding occurs during heating at the temperatures of 390 and 360 K for graphene on SiO2 and Si3N4 substrates, respectively. The biaxial Grüneisen parameter is determined to be 1.95 and 3.15 for G and 2D Raman bands of graphene, respectively. As the heating temperature exceeds a threshold temperature (1040 K for graphene/SiO2 and 640 K for graphene/Si3N4), buckling ridges are observed in graphene after the thermal cycle, from which the biaxial buckling strain of graphene on SiO2 and Si3N4 substrates are obtained as 0.21% and 0.22%, respectively. Importantly, the induced buckling ridges in graphene exhibit a pattern representing the symmetry of graphene crystal structure, which indicates that graphene relieves the compressive stress mainly along its lattice symmetry directions. These thermally induced graphene ridges are also found reminiscent of those in the synthesized graphene, suggesting the same origin of formation of the buckling ridges under biaxial compression. read less USED (high confidence) G. Mallick and R. Elder, “Graphene/hexagonal boron nitride heterostructures: Mechanical properties and fracture behavior from nanoindentation simulations,” Applied Physics Letters. 2018. link Times cited: 16 Abstract: In-plane or vertically stacked heterostructures containing m… read moreAbstract: In-plane or vertically stacked heterostructures containing multiple 2D materials are promising for emerging applications, such as flexible electronics, piezoelectric sensors, and molecular separations. However, utilizing heterostructures requires a fundamental understanding of their mechanics, which is currently lacking. Here, we use reactive molecular dynamics to simulate nanoindentation of stacked hexagonal boron nitride (h-BN) and graphene structures, 2D materials with similar structures but differing electronic properties. We calculate the Young's modulus, bending rigidity, ultimate strength, and the fracture strain of monolayers, homogeneous and heterogeneous bilayers, and alternating trilayers. Their mechanics are broadly similar, although graphene provides mild reinforcement to heterostructures. Further, we characterize the puncture created by nanoindentation, where we find that graphene allows smaller pores with a rougher fracture surface and more cleaved bonds than h-BN, which we attribute to differences in toughness. Our results demonstrate that these layered heterostructures maintain their mechanical robustness regardless of stacking order and provide insight into the influence of layer ordering in separation or passivation applications.In-plane or vertically stacked heterostructures containing multiple 2D materials are promising for emerging applications, such as flexible electronics, piezoelectric sensors, and molecular separations. However, utilizing heterostructures requires a fundamental understanding of their mechanics, which is currently lacking. Here, we use reactive molecular dynamics to simulate nanoindentation of stacked hexagonal boron nitride (h-BN) and graphene structures, 2D materials with similar structures but differing electronic properties. We calculate the Young's modulus, bending rigidity, ultimate strength, and the fracture strain of monolayers, homogeneous and heterogeneous bilayers, and alternating trilayers. Their mechanics are broadly similar, although graphene provides mild reinforcement to heterostructures. Further, we characterize the puncture created by nanoindentation, where we find that graphene allows smaller pores with a rougher fracture surface and more cleaved bonds than h-BN, which we attribute to dif... read less USED (high confidence) A. Mahata and T. Mukhopadhyay, “Probing the chirality-dependent elastic properties and crack propagation behavior of single and bilayer stanene.,” Physical chemistry chemical physics : PCCP. 2018. link Times cited: 26 Abstract: Stanene, a quasi-two-dimensional honeycomb-like structure of… read moreAbstract: Stanene, a quasi-two-dimensional honeycomb-like structure of tin belonging to the family of 2D-Xenes (X = Si, Ge, Sn) has recently been reported to show promising electronic, optical and mechanical properties. This paper investigates the elastic moduli and crack propagation behaviour of single layer and bilayer stanene based on molecular dynamics simulations, which have been performed using the Tersoff bond order potential (BOP). We have parameterized the interlayer van der Waals interactions for the bilayer Lennard-Jones potential in the case of bilayer stanene. Density functional calculations are performed to fit the Lennard-Jones parameters for the properties which are not available from the scientific literature. The effect of temperature and strain rate on the mechanical properties of stanene is investigated for both single layer and bilayer stanene in the armchair and zigzag directions. The results reveal that both the fracture strength and strain of stanene decrease with increasing temperature, while at higher loading rate, the material is found to exhibit higher fracture strength and strain. The effect of chirality on the elastic moduli of stanene is explained on the basis of a physics-based analytical approach, wherein the fundamental interaction between the shear modulus and Young's modulus is elucidated. To provide a realistic perspective, we have investigated the compound effect of uncertainty on the elastic moduli of stanene based on an efficient analytical approach. Large-scale Monte Carlo simulations are carried out considering different degrees of stochasticity. The in-depth results on mechanical properties presented in this article will further aid the adoption of stanene as a potential nano-electro-optical substitute with exciting features such as 2D topological insulating properties with a large bandgap, the capability to support enhanced thermoelectric performance, topological superconductivity and a quantum anomalous Hall effect at near-room-temperature. read less USED (high confidence) C. Yu et al., “Hot pressing-induced alignment of hexagonal boron nitride in SEBS elastomer for superior thermally conductive composites,” RSC Advances. 2018. link Times cited: 15 Abstract: Styrene–ethylene–butylene–styrene (SEBS) composite films con… read moreAbstract: Styrene–ethylene–butylene–styrene (SEBS) composite films containing well-dispersed and highly aligned hexagonal boron nitride (hBN) platelets were achieved by a ball milling process followed by hot-pressing treatment. An ultrahigh in-plane thermal conductivity of 45 W m−1 K−1 was achievable in the SEBS composite film with 95 wt% hBN. The corresponding out-of-plane thermal conductivity was also as high as 4.4 W m−1 K−1. The hBN/SEBS composite film was further used to cool a CPU connected to a computer, resulting in a decrease by about 4 °C in the stable temperature. Percolation thresholds over 40 wt% and 60 wt% in the hBN/SEBS composites were obtained in the in-plane and out-of-plane directions, respectively. This phenomenon has rarely been reported in polymer composites. Molecular dynamics simulations were also conducted to support this percolation threshold. The linear coefficients of the thermal expansion value of the hBN/SEBS composite with 95 wt% hBN was as low as 16 ppm K−1. This was a significant decrease compared to that of pure SEBS (149 ppm K−1). The proposed strategy provides valuable advice about the heat-transfer mechanism in polymer composites containing oriented two-dimensional materials. read less USED (high confidence) B. Mortazavi, M. Shahrokhi, X. Zhuang, and T. Rabczuk, “Boron–graphdiyne: a superstretchable semiconductor with low thermal conductivity and ultrahigh capacity for Li, Na and Ca ion storage,” Journal of Materials Chemistry. 2018. link Times cited: 90 Abstract: Most recently, boron–graphdiyne, a π-conjugated two-dimensio… read moreAbstract: Most recently, boron–graphdiyne, a π-conjugated two-dimensional (2D) structure made from a merely sp carbon skeleton connected with boron atoms was successfully experimentally realized through a bottom-up synthetic strategy. Motivated by this exciting experimental advance, we conducted density functional theory (DFT) and classical molecular dynamics simulations to study the mechanical, thermal conductivity and stability, electronic and optical properties of single-layer B-graphdiyne. We particularly analyzed the application of this novel 2D material as an anode for Li, Na, Mg and Ca ion storage. Uniaxial tensile simulation results reveal that B-graphdiyne owing to its porous structure and flexibility can yield superstretchability. The single-layer B-graphdiyne was found to exhibit a semiconducting electronic character, with a narrow band-gap of 1.15 eV based on the HSE06 prediction. It was confirmed that mechanical straining can be employed to further tune the optical absorbance and electronic band-gap of B-graphdiyne. Ab initio molecular dynamics results reveal that B-graphdiyne can withstand high temperatures, like 2500 K. The thermal conductivity of suspended single-layer B-graphdiyne was predicted to be very low, ∼2.5 W mK−1 at room temperature. Our first-principles results reveal the outstanding prospect of B-graphdiyne as an anode material with ultrahigh charge capacities of 808 mA h g−1, 5174 mA hg−1 and 3557 mA h g−1 for Na, Ca and Li ion storage, respectively. The comprehensive insight provided by this investigation highlights the outstanding physics of B-graphdiyne nanomembranes, and suggests them as highly promising candidates for the design of novel stretchable nanoelectronics and energy storage devices. read less USED (high confidence) Y. Liu et al., “Thermal Conductance of the 2D MoS2/h-BN and graphene/h-BN Interfaces,” Scientific Reports. 2017. link Times cited: 86 USED (high confidence) T. Zhang, J. Li, Y. Cao, L. Zhu, and G. Chen, “Tailoring thermal transport properties of graphene by nitrogen doping,” Journal of Nanoparticle Research. 2017. link Times cited: 9 USED (high confidence) R. Rezaei, C. Deng, M. Shariati, and H. Tavakoli-Anbaran, “The ductility and toughness improvement in metallic glass through the dual effects of graphene interface,” Journal of Materials Research. 2017. link Times cited: 12 Abstract: Bulk metallic glasses own unique mechanical properties such … read moreAbstract: Bulk metallic glasses own unique mechanical properties such as high strength and excellent elastic behavior due to their amorphous atomic structure. Nonetheless, they usually fail catastrophically by shear localization without showing any macroscale plastic deformation under tension and therefore are notoriously brittle. In this study, graphene was proposed as an effective reinforcement to improve the ductility and toughness of metallic glass for possessing a unique combination of strong in-plane strength and weak interbonding with the metal matrix based on molecular dynamics simulations. Both continuous and discontinuous graphene sheets with various configurations and lengths were taken into account. It was found that with proper dispersion of the graphene reinforcements, more than 100% increase in the ductility and more than 150% increase in the toughness can be achieved in the nanocomposites as compared to the monolithic metallic glass of similar size, which was enabled by spreading and delocalizing the plastic shearing deformation in the nanocomposites because of the dual effects of the added graphene. read less USED (high confidence) R. Rezaei, C. Deng, H. Tavakoli-Anbaran, and M. Shariati, “Deformation twinning-mediated pseudoelasticity in metal–graphene nanolayered membrane,” Philosophical Magazine Letters. 2016. link Times cited: 29 Abstract: In this study, we investigated the deformation behaviour of … read moreAbstract: In this study, we investigated the deformation behaviour of metal–graphene nanolayered composites for five face-centred cubic metals under compression using molecular dynamics simulations. It was found that by increasing the thickness of the individual metal layers, the composite strength increased, while the deformation mechanism changed from buckling to deformation twining in Cu, Au and Ag, which was absent in the monolithic form of those metals of the same orientation and size. The deformation twinning was found to be enabled by the graphene layer, which introduced pseudoelasticity and shape memory effects in the nanolayered membrane with more than 15% recoverable compressive strain. read less USED (high confidence) C. da Silva, F. Saiz, D. A. Romero, and C. Amon, “Coherent phonon transport in short-period two-dimensional superlattices of graphene and boron nitride,” Physical Review B. 2016. link Times cited: 28 Abstract: Promoting coherent transport of phonons at material interfac… read moreAbstract: Promoting coherent transport of phonons at material interfaces is a promising strategy for controlling thermal transport in nanostructures and an alternative to traditional methods based on structural defects. Coherent transport is particularly relevant in short-period heterostructures with smooth interfaces and long-wavelength heat-carrying phonons, such as two-dimensional superlattices of graphene and boron nitride. In this work, we predict phonon properties and thermal conductivities in these superlattices using a normal mode decomposition approach. We study the variation of the frequency dependence of these properties with the periodicity and interface configuration (zigzag and armchair) for superlattices with period lengths within the coherent regime. Our results showed that the thermal conductivity decreases significantly from the first period length (0.44 nm) to the second period length (0.87 nm), 13% across the interfaces and 16% along the interfaces. For greater periods, the conductivity across the interfaces continues decreasing at a smaller rate of 11 W/mK per period length increase (0.43 nm), driven by changes in the phonon group velocities (coherent effects). In contrast, the conductivity along the interfaces slightly recovers at a rate of 2 W/mK per period, driven by changes in the phonon relaxation times (diffusive effects). By changing the interface configuration from armchair to zigzag, the conductivities for all period lengths increase by approximately 7% across the interfaces and 19% along the interfaces. read less USED (high confidence) R. D’Souza and S. Mukherjee, “Thermoelectric transport in graphene/h-BN/graphene heterostructures: A computational study,” Physica E-low-dimensional Systems & Nanostructures. 2016. link Times cited: 19 USED (high confidence) A. Özden, A. Kandemir, F. Ay, N. K. Perkgöz, and C. Sevik, “Thermal Conductivity Suppression in Nanostructured Silicon and Germanium Nanowires,” Journal of Electronic Materials. 2016. link Times cited: 8 USED (high confidence) X. Gu and R. Yang, “Phonon transport and thermal conductivity in two-dimensional materials,” arXiv: Materials Science. 2015. link Times cited: 50 Abstract: Two-dimensional materials, such as graphene, boron nitride a… read moreAbstract: Two-dimensional materials, such as graphene, boron nitride and transition metal dichalcogenides, have attracted increased interest due to their potential applications in electronics and optoelectronics. Thermal transport in two-dimensional materials could be quite different from three-dimensional bulk materials. This article reviews the progress on experimental measurements and theoretical modeling of phonon transport and thermal conductivity in two-dimensional materials. We focus our review on a few typical two-dimensional materials, including graphene, boron nitride, silicene, transition metal dichalcogenides, and black phosphorus. The effects of different physical factors, such as sample size, strain and defects, on thermal transport in Two-dimensional materials are summarized. We also discuss the environmental effect on the thermal transport of two-dimensional materials, such as substrate and when two-dimensional materials are presented in heterostructures and intercalated with inorganic components or organic molecules. read less USED (high confidence) M.-Q. Le, “Prediction of Young’s modulus of hexagonal monolayer sheets based on molecular mechanics,” International Journal of Mechanics and Materials in Design. 2015. link Times cited: 31 USED (high confidence) M.-Q. Le, “Prediction of Young’s modulus of hexagonal monolayer sheets based on molecular mechanics,” International Journal of Mechanics and Materials in Design. 2014. link Times cited: 0 USED (high confidence) M.-Q. Le, “Young’s modulus prediction of hexagonal nanosheets and nanotubes based on dimensional analysis and atomistic simulations,” Meccanica. 2014. link Times cited: 17 USED (high confidence) M.-Q. Le, “Young’s modulus prediction of hexagonal nanosheets and nanotubes based on dimensional analysis and atomistic simulations,” Meccanica. 2014. link Times cited: 0 USED (high confidence) T. Li, Z. Tang, Z. Huang, and J. Yu, “A comparison between the mechanical and thermal properties of single-walled carbon nanotubes and boron nitride nanotubes,” Physica E-low-dimensional Systems & Nanostructures. 2017. link Times cited: 37 USED (low confidence) W. Zhao, S. Wang, L. Zhou, and X. Du, “Reducing interfacial thermal resistance between polyethylene oxide-based solid-state polymer electrolyte and lithium anode by using IVA group two-dimensional materials: A molecular dynamics study,” International Journal of Heat and Mass Transfer. 2024. link Times cited: 0 USED (low confidence) C. Wang et al., “Revealing the crystalline-amorphous W/B4C interface characteristic by first principles investigation,” Applied Surface Science Advances. 2023. link Times cited: 0 USED (low confidence) G. Zhang, S. Dong, X. Wang, and G. Xin, “Thermal transport of graphene-C3B superlattices and van der Waals heterostructures: a molecular dynamics study,” Nanotechnology. 2023. link Times cited: 0 Abstract: Two-dimensional (2D) materials have attracted more and more … read moreAbstract: Two-dimensional (2D) materials have attracted more and more attention due to their excellent properties. In this work, we systematically explore the heat transport properties of Graphene-C3B (GRA-C3B) superlattices and van der Waals (vdW) heterostructures using molecular dynamics method. The effects of interface types and heat flow directions on the in-plane interfacial thermal resistance (ITRip) are analyzed. Obvious thermal rectification is detected in the more energy stable interface, GRA zigzag-C3B zigzag (ZZ) interface, which also has the minimum value of ITRip. The dependence of the superlattices thermal conductivity (k) of the ZZ interface on the period length (l p ) is investigated. The results show that when the l p is 3.5 nm, the k reaches a minimum value of 35.52 W m−1 K−1, indicating a transition stage from coherent phonon transport to incoherent phonon transport. Afterwards, the effects of system size, temperature, coupling strength and vacancy defect on the out-of-plane interfacial thermal resistance (ITRop) are evaluated. With the increase of temperature, coupling strength and vacancy defect, ITRop are found to reduce effectively due to the enhanced Umklapp phonon scattering and increased probability of energy transfer. Phonon density of states and phonon participation ratio is evaluated to reveal phonon behavior during heat transport. This work is expected to provide essential guidance for the thermal management of nanoelectronics based on 2D monolayer GRA and C3B. read less USED (low confidence) P. R. Galligan et al., “Aligned carbon-doping to modulate thermal and electrical conductivity of boron carbon nitride grown from chemical vapor deposition,” Carbon. 2023. link Times cited: 0 USED (low confidence) S. Lahkar and R. Ranganathan, “Competing mechanisms govern the thermal rectification behavior in semi-stochastic polycrystalline graphene with graded grain-size distribution,” Carbon. 2023. link Times cited: 0 USED (low confidence) J. F. Dethan, “Thermal conductivity of hydrogenated h-BN nanosheets: a reactive force field study,” Soft Materials. 2023. link Times cited: 0 Abstract: ABSTRACT Thermal conductivity of hydrogenated hexagonal boro… read moreAbstract: ABSTRACT Thermal conductivity of hydrogenated hexagonal boron nitride (h-BN) nanosheets was investigated using molecular dynamics simulation method. A newly parameterized reactive force field (ReaxFF) for hydrogen and h-BN interactions was used. ReaxFF was used due to its higher accuracy compared to other simpler interatomic potentials. Accurate thickness selection of a monolayer h-BN nanosheet has been shown to produce high thermal conductivity values for pristine armchair and zigzag nanosheets. It was further found that hydrogenation diminishes thermal conductivity of hydrogenated h-BN nanosheets. This reduction in thermal conductivity was due to the occurrence of sp2 to sp3 bonding transition when hydrogen atoms were placed on top of B and N atoms. The increase in temperature was also found to diminish thermal conductivity due to the occurrence of phonon–phonon scattering at higher temperatures. N-vacancy defect has then been shown to exhibit lower thermal conductivity compared to B-vacancy defect. Furthermore, the removal of more atoms contributes to higher decline in thermal conductivity. However, vacancy defect constructed along vertical direction provides the highest reduction in thermal conductivity. It is expected that this work provides useful insights for the design of an effective hydrogen storage system using these novel h-BN nanosheets. read less USED (low confidence) X. Song, J. Yuan, C. Yang, G. Deng, Z. Wang, and J. Gao, “Carbon dioxide separation performance evaluation of amine-based versus choline-based deep eutectic solvents,” Renewable and Sustainable Energy Reviews. 2023. link Times cited: 1 USED (low confidence) D. Tan, M. Willatzen, and J. Christensen, “Structuring thermal transport in pristine graphene with h-BN nanorings,” Journal of Physics and Chemistry of Solids. 2023. link Times cited: 0 USED (low confidence) M. Zhou, L. Liu, J. Liu, and Z. Mei, “Prediction and Control of Thermal Transport at Defective State Gr/h-BN Heterojunction Interfaces,” Nanomaterials. 2023. link Times cited: 1 Abstract: The control of interfacial thermal conductivity is the key t… read moreAbstract: The control of interfacial thermal conductivity is the key to two−dimensional heterojunction in semiconductor devices. In this paper, by using non−equilibrium molecular dynamics (NEMD) simulations, we analyze the regulation of interfacial thermal energy transport in graphene (Gr)/hexagonal boron nitride (h-BN) heterojunctions and reveal the variation mechanism of interfacial thermal energy transport. The calculated results show that 2.16% atomic doping can effectively improve interfacial heat transport by more than 15.6%, which is attributed to the enhanced phonon coupling in the mid−frequency region (15–25 THz). The single vacancy in both N and B atoms can significantly reduce the interfacial thermal conductivity (ITC), and the ITC decreases linearly with the increase in vacancy defect concentration, mainly due to the single vacancy defects leading to an increased phonon participation rate (PPR) below 0.4 in the low-frequency region (0–13 THz), which shows the phonon the localization feature, which hinders the interfacial heat transport. Finally, a BP neural network algorithm is constructed using machine learning to achieve fast prediction of the ITC of Gr/h-BN two-dimensional heterogeneous structures, and the results show that the prediction error of the model is less than 2%, and the method will provide guidance and reference for the design and optimization of the ITC of more complex defect-state heterogeneous structures. read less USED (low confidence) Z. Cao et al., “Thermal transport in graphene–HMX composites with grafted interface,” Journal of Materials Science. 2023. link Times cited: 1 USED (low confidence) X. Wu, P. Ying, C. Li, and Q. Han, “Dual effects of hetero-interfaces on phonon thermal transport across graphene/C3N lateral superlattices,” International Journal of Heat and Mass Transfer. 2023. link Times cited: 1 USED (low confidence) C. Guarda, B. Faria, N. Silvestre, and J. C. C. Lopes, “Influence of Matrix Recrystallization and Nanofiller Porosity on the Interfacial Properties of Holey Graphene-Aluminium Nanocomposites,” Composite Structures. 2023. link Times cited: 2 USED (low confidence) L. Gong et al., “Thermal conductivity and interfacial thermal conductivity of complex boron nitride nanoribbons,” Journal of Thermal Stresses. 2023. link Times cited: 0 Abstract: Aiming at developing insulating materials with high thermal … read moreAbstract: Aiming at developing insulating materials with high thermal conductivity (TC), which can make up for the shortcoming that graphene cannot be used directly in electronic devices because of its zero band gap, we systematically study the thermal transport of the hexagonal boron nitride nanoribbons (BNNRs) composed of one multilayer central region (CR) and two monolayer regions (MRs). We show that the TC and the interfacial thermal conductivity (ITC) depend on the BNNR structure parameters and the temperature in different ways. As the CR layer number increases the ITC will decrease, indicating the two-layer BNNR will show the largest ITC. The TC will increase and the ITC will fluctuate around a certain value with increasing the MR length. However, with the increase of the BNNR width, both TC and ITC will show oscillations near certain values. Furthermore, we find that the ITC (TC) will increase (decrease) with the temperature increasing. Finally, we calculate the ITC of the compound BNNRs in different stacking manners and find the ITC for the AB stacking is greater than that for the AA stacking. This research presents the possible measures for manipulating heat transport and demonstrates that the whole heat transport performance is fundamentally determined by the interfaces. read less USED (low confidence) R. Tromer, I. M. Felix, L. C. Felix, L. Machado, C. Woellner, and D. Galvão, “Hydrogen atom/molecule adsorption on 2D metallic porphyrin: A first-principles study,” Chemical Physics. 2023. link Times cited: 0 USED (low confidence) F. Z. Zanane, K. Sadki, L. B. Drissi, E. H. Saidi, and M. Bousmina, “Graphene multilayers nanoribbons with chirality from molecular dynamics,” Materials Science and Engineering: B. 2022. link Times cited: 0 USED (low confidence) Z. Wang et al., “Phonon Transport in Two-dimensional Carbon-boron Material and Heterointerfaces,” Surfaces and Interfaces. 2022. link Times cited: 2 USED (low confidence) A. Senturk and G. Akgün, “Exploring the thermal conductivity and mechanical properties of BN-doped graphyne,” Journal of Molecular Modeling. 2022. link Times cited: 0 USED (low confidence) B. Azizi, M. Shariati, S. S. M. N. Souq, and M. Hosseini, “Bending and Stretching Behavior of Graphene Structures Using Continuum Models Calibrated with Modal Analysis,” Applied Mathematical Modelling. 2022. link Times cited: 5 USED (low confidence) W. Sha, X. Dai, S. Chen, and F. Guo, “Phonon thermal transport in graphene/h-BN superlattice monolayers,” Diamond and Related Materials. 2022. link Times cited: 2 USED (low confidence) Y. Liu et al., “Investigations on microstructure and mechanical properties of boron nitride fiber using experimental and numerical methods,” Materials Today Communications. 2022. link Times cited: 0 USED (low confidence) J. Lu et al., “Molecular dynamics simulation of the temperature effect on ideal mechanical properties of SiC/BN interface for SiCf/SiC composites,” Composite Interfaces. 2022. link Times cited: 0 Abstract: ABSTRACT Interfacial strength plays a significant role in th… read moreAbstract: ABSTRACT Interfacial strength plays a significant role in the mechanical properties of SiCf/SiC composites. The understanding of the micro-mechanisms of interfacial strength on mechanical properties at different temperature is important in application of SiCf/SiC composite. In the present work, the interfacial properties of ideal tensile strength and fracture toughness of SiC/BN interface at different temperature were studied based on molecular dynamics. It is revealed that the interfacial strength of Case Si (Si-terminated SiC/BN interface) decreases with the increase of temperature, resulting in the decrease of tensile strength and fracture toughness, while the interfacial strength of Case C (C-terminated SiC/BN interface) basically remains unchanged; so the interfacial properties of Case C are less affected by temperature. This phenomenon is well explained in terms of stress distribution and interface bonding number. Our results provide a good theoretical explanation for the high-temperature service performance of ceramic matrix composites. Graphical abstract read less USED (low confidence) C. Guarda, B. Faria, N. Silvestre, J. Lopes, and N. Pugno, “Melted and recrystallized holey-graphene-reinforced aluminum composites: Structure, elasticity and strength,” Composite Structures. 2022. link Times cited: 4 USED (low confidence) J. F. Dethan, J. Yeo, M. Rhamdhani, and V. Swamy, “Thermal conductivities of hydrogen encapsulated boron nitride and hybrid boron nitride – carbon nanotubes using molecular dynamics simulations,” Materials Today Communications. 2022. link Times cited: 2 USED (low confidence) S. Ren, Y. Shi, C. Zhang, M. Cui, and J. Pu, “Anomalous enhancement oxidation of few-layer MoS2 and MoS2/h-BN heterostructure,” Nano Research. 2022. link Times cited: 4 USED (low confidence) M. Z. Dehaghani, F. Molaei, C. Spitas, and A. H. Mashhadzadeh, “Thermal rectification in nozzle-like graphene/boron nitride nanoribbons: A molecular dynamics simulation,” Computational Materials Science. 2022. link Times cited: 9 USED (low confidence) M. Roshan, A. Akbarzadeh, S. Sadeghzadeh, and A. Maleki, “Tailoring the hardness of aluminum surface reinforced with graphene and C3N nanosheets,” Diamond and Related Materials. 2022. link Times cited: 1 USED (low confidence) A. T. Sose, E. Mohammadi, F. Wang, and S. A. Deshmukh, “Investigation of structure and dynamics of water confined between hybrid layered materials of graphene, boron nitride, and molybdenum disulfide,” Journal of Materials Science. 2022. link Times cited: 4 USED (low confidence) N. Zhang et al., “Near-Interface Defects in Graphene/H-BN In-Plane Heterostructures: Insights into the Interfacial Thermal Transport,” Nanomaterials. 2022. link Times cited: 3 Abstract: Based on nonequilibrium molecular dynamics (NEMD) and nonequ… read moreAbstract: Based on nonequilibrium molecular dynamics (NEMD) and nonequilibrium Green’s function simulations, the interfacial thermal conductance (ITC) of graphene/h-BN in-plane heterostructures with near-interface defects (monovacancy defects, 585 and f5f7 double-vacancy defects) is studied. Compared to pristine graphene/h-BN, all near-interface defects reduce the ITC of graphene/h-BN. However, differences in defective structures and the wrinkles induced by the defects cause significant discrepancies in heat transfer for defective graphene/h-BN. The stronger phonon scattering and phonon localization caused by the wider cross-section in defects and the larger wrinkles result in the double-vacancy defects having stronger energy hindrance effects than the monovacancy defects. In addition, the approximate cross-sections and wrinkles induced by the 585 and f5f7 double-vacancy defects provide approximate heat hindrance capability. The phonon transmission and vibrational density of states (VDOS) further confirm the above results. The double-vacancy defects in the near-interface region have lower low-frequency phonon transmission and VDOS values than the monovacancy defects, while the 585 and f5f7 double-vacancy defects have similar low-frequency phonon transmission and VDOS values at the near-interface region. This study provides physical insight into the thermal transport mechanisms in graphene/h-BN in-plane heterostructures with near-interface defects and provides design guidelines for related devices. read less USED (low confidence) F. Z. Zanane, K. Sadki, L. B. Drissi, and E. H. Saidi, “Graphene-based SiC Van der Waals heterostructures: nonequilibrium molecular dynamics simulation study,” Journal of Molecular Modeling. 2022. link Times cited: 3 USED (low confidence) X. Wu and Q. Han, “Transition from incoherent to coherent phonon thermal transport across graphene/h-BN van der Waals superlattices,” International Journal of Heat and Mass Transfer. 2022. link Times cited: 13 USED (low confidence) Y.-K. Weng, S. Shin, K. Kihm, M. M. Bahzad, and D. Aaron, “Investigation of microscopic mechanisms for water-ice phase change propagation control,” International Journal of Heat and Mass Transfer. 2022. link Times cited: 3 USED (low confidence) L. Fan, K. Liu, G. Liu, and Y. Hong, “Defects in Gr/h-BN nanoribbons heterostructure: Atomically precise cutting and defect amplification effect via hydrogenation pseudo-crack,” Diamond and Related Materials. 2022. link Times cited: 4 USED (low confidence) B. Zhao, Y. Zhang, Y. Fan, X. Yu, Z. Zhang, and B. Zhang, “The three-body abrasive tribological characteristics of the Graphene/h-BN heterostructure film considering defects,” Tribology International. 2022. link Times cited: 8 USED (low confidence) A. Dadrasi, A. Albooyeh, S. Fooladpanjeh, A. Salmankhani, A. H. Mashhadzadeh, and M. Saeb, “Theoretical examination of the fracture behavior of BC3 polycrystalline nanosheets: Effect of crack size and temperature,” Mechanics of Materials. 2022. link Times cited: 6 USED (low confidence) M.-Q. Le and R. Batra, “Fracture toughness of single layer boronitrene sheet using MD simulations,” Computational Materials Science. 2022. link Times cited: 0 USED (low confidence) W. Sha and F. Guo, “Thermal transport in two-dimensional carbon nitrides: A comparative molecular dynamics study,” Carbon Trends. 2022. link Times cited: 4 USED (low confidence) B. Sharma and A. G. Rajan, “How Grain Boundaries and Interfacial Electrostatic Interactions Modulate Water Desalination via Nanoporous Hexagonal Boron Nitride.,” The journal of physical chemistry. B. 2022. link Times cited: 5 Abstract: To fulfill the increasing demand for drinking water, researc… read moreAbstract: To fulfill the increasing demand for drinking water, researchers are currently exploring nanoporous two-dimensional materials, such as hexagonal boron nitride (hBN), as potential desalination membranes. A prominent, yet unsolved challenge is to understand how such membranes will perform in the presence of defects or surface charge in the membrane material. In this work, we study the effect of grain boundaries (GBs) and interfacial electrostatic interactions on the desalination performance of bicrystalline nanoporous hBN using classical molecular dynamics simulations supported by quantum-mechanical density functional theory (DFT) calculations. We investigate three different nanoporous bicrystalline hBN configurations, with symmetric tilt GBs having misorientation angles of 13.2, 21.8, and 32.2°. Using lattice dynamics calculations, we find that grain boundaries alter the areas and shapes of nanopores in bicrystalline hBN, as compared to the nanopores in monocrystalline hBN. We observe that, although bicrystalline nanoporous hBN with a misorientation angle of 13.2° shows an improved water flow rate by ∼30%, it demonstrates reduced Na+ ion rejection by ∼6%, as compared to monocrystalline hBN. We also uncover the role of the nanopore shape in water desalination, finding that more elongated pores with smaller sizes (in 21.8- and 32.2°-misoriented bicrystalline hBN) can match water permeation through less elongated pores of slightly larger sizes, with a concomitant ∼3-4% decrease in Na+ rejection. Simulations also predict that the water flow rate is significantly affected by interfacial electrostatic interactions. Indeed, the water flow rate is the highest when altered partial charges on B and N atoms were determined using DFT calculations, as compared to when no partial charges or bulk partial charges (i.e., charged hBN) were considered. Overall, our work on water/ion transport through nanopores in bicrystalline hBN indicates that the presence of GBs and surface charge can lead, respectively, to a decrease in the ion rejection and water permeation performance of hBN membranes. read less USED (low confidence) S. M. Hatam-Lee, F. Jabbari, and A. Rajabpour, “Interfacial thermal conductance between gold and SiO2: A molecular dynamics study,” Nanoscale and Microscale Thermophysical Engineering. 2022. link Times cited: 2 Abstract: ABSTRACT Silica coating on a gold nanoparticle can improve i… read moreAbstract: ABSTRACT Silica coating on a gold nanoparticle can improve its thermal application in cancer thermotherapy. In this paper, the interfacial thermal conductance between gold and silica is calculated utilizing classical non-equilibrium molecular dynamics. It is revealed that the results of molecular dynamics are different from what has been predicted by the conventional diffuse mismatch model. Furthermore, the interfacial thermal conductance between amorphous SiO2 and gold is approximately twice that of crystalline silica, which is explained by calculating the vibrational density of state mismatches. The interfacial thermal conductance variations in terms of van der Waals interaction strength between gold and silica are also investigated. It is revealed that the conductance increases by about 30% by increasing the simulation temperature from 300 to 700 K. The results of this paper can be useful in nanofluid systems, in addition to the application of silica-coated gold nanoparticles in cancer thermal therapy. read less USED (low confidence) M.-Q. Le, “Fracture and strength of single-atom-thick hexagonal materials,” Computational Materials Science. 2022. link Times cited: 1 USED (low confidence) H. Guo, C. Huo, L. Yang, and S. Lin, “Thermal Conductivity of Graphitic Carbon Nitride Nanotubes: A Molecular Dynamics Study,” Advances in Condensed Matter Physics. 2021. link Times cited: 2 Abstract: Graphitic carbon nitride (g-C3N4) nanotubes are recently gai… read moreAbstract: Graphitic carbon nitride (g-C3N4) nanotubes are recently gaining increasing interest due to their extraordinary physicochemical properties. In the following, we report on simulations using a method of nonequilibrium molecular dynamics and focus on the thermal conductivity variation of g-C3N4 nanotubes with respect to different temperatures, diameters, and chiral angles. In spite of the variation of diameters and chiral angles, the structure of nanotubes possesses high stability in the temperature range from 200 K to 600 K. Although there is little change of the thermal conductivity per unit arc length for nanotubes with the same diameter at different temperatures, it decreases significantly with increasing diameters at the same temperature. The thermal conductivity at different chiral angles has little to do with how temperature changes. Simulation results show that the vibrational density of states of nanotubes distributed, respectively, at ∼11 THz and ∼32 THz, indicating that heat in nanotubes is mostly carried by phonons with frequencies lower than 10 THz. read less USED (low confidence) M. Z. Dehaghani et al., “An insight into thermal properties of BC3-graphene hetero-nanosheets: a molecular dynamics study,” Scientific Reports. 2021. link Times cited: 15 USED (low confidence) M. Shariati, B. Azizi, M. Hosseini, and M. Shishesaz, “On the calibration of size parameters related to non-classical continuum theories using molecular dynamics simulations,” International Journal of Engineering Science. 2021. link Times cited: 22 USED (low confidence) Y. Du, P. Ying, and J. Zhang, “Prediction and optimization of the thermal transport in hybrid carbon-boron nitride honeycombs using machine learning,” Carbon. 2021. link Times cited: 3 USED (low confidence) A. Senturk, “Thermo-mechanical properties of different structures of BC2N,” Molecular Simulation. 2021. link Times cited: 7 Abstract: ABSTRACT The thermo-mechanical properties of four various st… read moreAbstract: ABSTRACT The thermo-mechanical properties of four various structures of BC2N are investigated using molecular dynamics (MD) simulation. These structures show superior mechanical properties. Especially, the type C, which has more C–C and B–N bonds, demonstrates higher mechanical properties than others. Conversely, the type D shows the lowest mechanical properties with increasing B–B and N–N bonds. BC2N structures are studied at different temperatures and strain rates. As temperature increases up to 900 K, the mechanical properties of BC2N structures gradually decrease. Also, changing of temperature shows more effect on the types A and D than others. Furthermore, the mechanical properties of BC2N structures demonstrate increasing trend when strain rate increases. Additionally, the influence of strain rate on the mechanical properties of BC2N structures is more prominent at lower temperatures. Non-equilibrium MD simulation findings show high thermal conductivity (TC) values of BC2N structures. The type C containing most C–C and B–N bonds has the highest TC value. However, the type D has more N–N and B–B bonds, resulting in a low TC. Due to increasing of phonon-phonon scattering, when the temperature increases from 300 to 900 K, the TCs of these structures are adversely affected. read less USED (low confidence) P. Zheng, W. Jiang, Q. Qin, and D. Li, “Dynamic Behavior of Rotation Transmission Nano-System in Helium Environment: A Molecular Dynamics Study,” Molecules. 2021. link Times cited: 0 Abstract: The molecular dynamics (MD) method is used to investigate th… read moreAbstract: The molecular dynamics (MD) method is used to investigate the influence of the shielding gas on the dynamic behavior of the heterogeneous rotation transmission nano-system (RTS) built on carbon nanotubes (CNTs) and boron nitride nanotube (BNNT) in a helium environment. In the heterogeneous RTS, the inner CNT acts as a rotor, the middle BNNT serves as a motor, and the outer CNT functions as a stator. The rotor will be actuated to rotate by the motor due to the interlayer van der Waals effects and the end effects. The MD simulation results show that, when the gas density is lower than a critical range, a stable signal of the rotor will arise on the output and the rotation transmission ratio (RRT) of RTS can reach 1.0, but as the gas density is higher than the critical range, the output signal of the rotor cannot be stable due to the sharp drop of the RRT caused by the large friction between helium and the RTS. The greater the motor input signal of RTS, the lower the critical working helium density range. The results also show that the system temperature and gas density are the two main factors affecting the RTS transmission behavior regardless of the size of the simulation box. Our MD results clearly indicate that in the working temperature range of the RTS from 100 K to 600 K, the higher the temperature and the lower the motor input rotation frequency, the higher the critical working helium density range allows. read less USED (low confidence) Q. Zhang, B. Mortazavi, and F. Aldakheel, “Molecular Dynamics Modeling of Mechanical Properties of Polymer Nanocomposites Reinforced by C7N6 Nanosheet,” Surfaces. 2021. link Times cited: 3 Abstract: Carbon-nitride nanosheets have attracted remarkable attentio… read moreAbstract: Carbon-nitride nanosheets have attracted remarkable attention in recent years due to their outstanding physical properties. C7N6 is one of the hotspot nanosheets which possesses excellent mechanical, electrical, and optical properties. In this study, the coupled thermo-mechanical properties of the single nanosheet C7N6 are systematically investigated. Although temperature effects have a strong influence on the mechanical properties of C7N6 monolayer, thermal effects were not fully analyzed for carbon-nitride nanosheet and still an open topic. To this end, the presented contribution aims to highlight this important aspect and investigate the temperature influence on the mechanical stress-strain response. By using molecular dynamics (MD) simulation, we have found out that the C7N6 monolayer’s maximum strength decreases as the temperature increase from 300 K to 1100 K. In the current contribution, 5% to 15% volume fractions of C7N6/P3HT composite were employed to investigate the C7N6 reinforcing ability. Significantly, the uniaxial tensile of C7N6/P3HT composite reveals that 10%C7N6 can enhance the maximum strength of the composite to 121.80 MPa which is 23.51% higher than the pure P3HT matrix. Moreover, to better understand the enhanced mechanism, we proposed a cohesive model to investigate the interface strength between the C7N6 nanosheet and P3HT matrix. This systematic study provides not only a sufficient method to understand the C7N6 thermo-mechanical properties, but also the reinforce mechanism of the C7N6 reinforced nanocomposite. Thus, this work provides a valuable method for the later investigation of the C7N6 nanosheet. read less USED (low confidence) L. Nan, N. Ding, T. Jiang, L. Liu, and F. Zaïri, “Mechanical properties of nanocracks in hybrid graphene/hexagonal boron nitride sheets,” Journal of Mechanics of Materials and Structures. 2021. link Times cited: 0 USED (low confidence) P. Zheng, W. Jiang, Y. Lin, Y.-J. Chen, Q. Qin, and D. Li, “A novel rotation transmission nano-system based on Carbon@Boron-Nitride@Carbon heterogeneous nanotubes: A molecular dynamics study,” Computational Materials Science. 2021. link Times cited: 4 USED (low confidence) Y. Zheng et al., “One-dimensional van der Waals heterostructures: Growth mechanism and handedness correlation revealed by nondestructive TEM,” Proceedings of the National Academy of Sciences of the United States of America. 2021. link Times cited: 24 Abstract: Significance We recently synthesized coaxially nested one-di… read moreAbstract: Significance We recently synthesized coaxially nested one-dimensional van der Waals heterostructures in which boron nitride nanotubes or molybdenum disulfide nanotubes grew seamlessly on a single-walled carbon nanotube template. In this work, edge structures, nucleation sites, and crystal epitaxial relationships in heteronanotubes are unambiguously revealed by a nondestructive transmission electron microscopic technique. These understandings, together with the characterization technique developed here, can help to optimize the synthesis process. Structure-controlled heteronanotubes may, ultimately, be used to build nanoscale devices such as gate-all-around nanotube transistors. We recently synthesized one-dimensional (1D) van der Waals heterostructures in which different atomic layers (e.g., boron nitride or molybdenum disulfide) seamlessly wrap around a single-walled carbon nanotube (SWCNT) and form a coaxial, crystalized heteronanotube. The growth process of 1D heterostructure is unconventional—different crystals need to nucleate on a highly curved surface and extend nanotubes shell by shell—so understanding the formation mechanism is of fundamental research interest. In this work, we perform a follow-up and comprehensive study on the structural details and formation mechanism of chemical vapor deposition (CVD)–synthesized 1D heterostructures. Edge structures, nucleation sites, and crystal epitaxial relationships are clearly revealed using transmission electron microscopy (TEM). This is achieved by the direct synthesis of heteronanotubes on a CVD-compatible Si/SiO2 TEM grid, which enabled a transfer-free and nondestructive access to many intrinsic structural details. In particular, we have distinguished different-shaped boron nitride nanotube (BNNT) edges, which are confirmed by electron diffraction at the same location to be strictly associated with its own chiral angle and polarity. We also demonstrate the importance of surface cleanness and isolation for the formation of perfect 1D heterostructures. Furthermore, we elucidate the handedness correlation between the SWCNT template and BNNT crystals. This work not only provides an in-depth understanding of this 1D heterostructure material group but also, in a more general perspective, serves as an interesting investigation on crystal growth on highly curved (radius of a couple of nanometers) atomic substrates. read less USED (low confidence) S. I. Kundalwal, V. Choyal, and V. Choyal, “Flexoelectric effect in boron nitride–graphene heterostructures,” Acta Mechanica. 2021. link Times cited: 12 USED (low confidence) C. Huang, X. Peng, and B. Yang, “Effect of heterointerface on the indentation behavior of nano-laminated c-BN/diamond composites,” Ceramics International. 2021. link Times cited: 6 USED (low confidence) X. Wu and Q. Han, “Thermal transport in pristine and defective two-dimensional polyaniline (C3N),” International Journal of Heat and Mass Transfer. 2021. link Times cited: 8 USED (low confidence) X. Wu and Q. Han, “Phonon Thermal Transport across Multilayer Graphene/Hexagonal Boron Nitride van der Waals Heterostructures.,” ACS applied materials & interfaces. 2021. link Times cited: 31 Abstract: Van der Waals (vdW) heterostructures stacked vertically by g… read moreAbstract: Van der Waals (vdW) heterostructures stacked vertically by graphene (Gr) and hexagonal boron nitride (h-BN), by virtue of their novel properties, will undoubtedly spark great interests from the perspective of basic physics and applied science. Herein, phonon thermal transport across multilayer Gr/h-BN vdW heterostructures was systematically investigated by extensive molecular dynamics simulations, both in terms of internal structural configuration and external modulation. The former includes the structural configuration at the Gr/h-BN interface, the proportion of components in the effective heat transfer area, and size effect, while the latter includes cross-plane strain, temperature, and interfacial coupling strength. Our results show that at 300 K it has an ultralow out-of-plane thermal conductivity of only about 8.93 MWm-1 K-1, while the Gr/h-BN interfacial thermal conductance (ITC) is up to about 300 MWm-2 K-1, and the latter can be modulated in a wide range from 0.5 to 3.5 times under cross-plane strain. The analysis of the spectral decomposition results indicates that the thermal transport across the Gr/h-BN interface depends almost entirely on low-frequency out-of-plane phonons below 10 THz and the quantum effect can be ignorable, which uncovers the physical mechanisms underlying the changes in the ITC and also points the path toward its modulation. read less USED (low confidence) S. Fooladpanjeh et al., “Thermal conductivity of random polycrystalline BC3 nanosheets: A step towards realistic simulation of 2D structures.,” Journal of molecular graphics & modelling. 2021. link Times cited: 15 USED (low confidence) M. Li, L. Jiahuan, W. Yu, Y. Zhang, and H. Zhou, “Atomistic molecular dynamic simulations of the thermal transport across h-BN/cellulose nanocrystal interface,” International Journal of Heat and Mass Transfer. 2021. link Times cited: 4 USED (low confidence) Y. Zeng, Y.-X. Feng, L.-M. Tang, and K. Chen, “Effect of out-of-plane strain on the phonon structures and anharmonicity of twisted multilayer graphene,” Applied Physics Letters. 2021. link Times cited: 34 Abstract: Twisted bilayer and multilayer two-dimensional materials lin… read moreAbstract: Twisted bilayer and multilayer two-dimensional materials linked by van der Waals interactions exhibit various unique physical properties. The phonon properties of such systems are of great importance, but have not been explored in detail. In this work, we use a hybrid neural-network potential to systematically investigate the evolution of the phonon structure of twisted multilayer graphene under out-of-plane strain. With increasing out-of-plane strain, the evolution of the phonon structure of the moire superlattice exhibits different behavior from that of AA and AB stacked multilayer graphene. Meanwhile, with twisting of the interlayer, a higher Gruneisen parameter and a lower phonon group velocity can be obtained. A possible method is revealed by which phonon anharmonic scattering in stacked multilayer graphene could be enhanced by varying the twist angle in combination with out-of-plane strain. Our work shows that the application of out-of-plane strain can serve as an effective way to amplify the effect of twist angle on phonon structures of twisted multilayer two-dimensional systems, with potential application to thermoelectric and thermal logical devices. read less USED (low confidence) A. Dadrasi, S. Fooladpanjeh, A. Albooyeh, A. Salmankhani, A. H. Mashhadzadeh, and M. Saeb, “A theoretical insight into the fracture behavior of the edge-cracked polycrystalline BC3 nanosheets,” Computational Materials Science. 2021. link Times cited: 10 USED (low confidence) F. Molaei, K. E. Eshkalak, S. Sadeghzadeh, and H. Siavoshi, “Assessing mechanical properties of single-layer B-doped C3N and N-doped BC3 nanosheets and their hybrid,” Computational Materials Science. 2021. link Times cited: 4 USED (low confidence) B. Bagheri et al., “Fracture fingerprint of polycrystalline C3N nanosheets: Theoretical basis.,” Journal of molecular graphics & modelling. 2021. link Times cited: 15 USED (low confidence) S. Corthay et al., “Elevated-temperature high-strength h-BN-doped Al2014 and Al7075 composites: Experimental and theoretical insights,” Materials Science and Engineering A-structural Materials Properties Microstructure and Processing. 2021. link Times cited: 10 USED (low confidence) S. Wu, K. Zhang, J. Li, and T. Zhong, “Boron and nitrogen edges modify the thermal conductivity of phagraphene nanoribbons: Molecular dynamics simulations,” Computational Materials Science. 2021. link Times cited: 3 USED (low confidence) A. T. Celebi, T. Vlugt, and O. Moultos, “Thermal conductivity of aqueous solutions of reline, ethaline, and glyceline deep eutectic solvents; a molecular dynamics simulation study,” Molecular Physics. 2021. link Times cited: 12 Abstract: Accurate knowledge and control of thermal conductivities is … read moreAbstract: Accurate knowledge and control of thermal conductivities is central for the efficient design of heat storage and transfer devices working with deep eutectic solvents (DESs). The addition of water is a straightforward and cost-efficient way of tuning many properties of DESs. In this work, the thermal conductivities of aqueous solutions of reline, ethaline, and glyceline are reported for the first time. The non-equilibrium molecular dynamics Müller-Plathe (MP) method was used, along with the well-established GAFF and SPC/E force fields for DESs and water, respectively. We show that thermal conductivities of neat DESs are in excellent agreement with available experimental data. The addition of 25 wt% water results in nearly 2 times higher thermal conductivities in all DESs. A further increase in the fraction of water to 75 wt%, causes an increase in the thermal conductivities of DESs ca. 3 times. This behaviour is mainly due to the change in the microscopic structure of the DESs (i.e. hydrogen bonding) upon the addition of water. Our simulations reveal that thermal conductivities of aqueous DESs do not significantly depend on temperature. We also show that thermal conductivities strongly depend on system-size. System-sizes bigger larger than ca. 5 nm should be used. GRAPHICAL ABSTRACT read less USED (low confidence) X. Wu and Q. Han, “Semidefective Graphene/h-BN In-Plane Heterostructures: Enhancing Interface Thermal Conductance by Topological Defects,” Journal of Physical Chemistry C. 2021. link Times cited: 8 Abstract: Two-dimensional (2D) in-plane heterostructures, whose interf… read moreAbstract: Two-dimensional (2D) in-plane heterostructures, whose interface thermal conductance (ITC) plays a crucial role in the thermal performance of nanostructured materials, will undoubtedly become the fo... read less USED (low confidence) X. Li et al., “Construction of Oriented Interconnected BNNS Skeleton by Self‐Growing CNTs Leading High Thermal Conductivity,” Advanced Materials Interfaces. 2021. link Times cited: 11 Abstract: The development of thermal conduction polymer‐based composit… read moreAbstract: The development of thermal conduction polymer‐based composites is important to solve the heat dissipation of electronic instruments under overheating conditions. The construction of thermal conductive pathways in composites and the reduction of contact resistance between fillers are crucial for concerning excellent thermal conduction properties. Herein, the oriented coherent thermal conductive network in composites is successfully developed via the in situ growth of carbon nanotubes (CNTs) into boron nitride nanosheets (BNNSs) skeleton prepared from ice‐templated. The thermal conductivity of composites reaches 3.21 W m−1 K−1 approximately low filler loading of 9.86 vol%, due to the formation of the covalent bonding between CNTs and BNNSs as reducing the thermal contact resistance by one order of magnitude. More importantly, non‐equilibrium molecular dynamics (NEMD) simulations are carried out to demonstrate the influence of CNTs in elevating the heat conductivity between BNNSs. Meanwhile, the volume resistivity of composites up to 1015 Ω cm far met the requirement of electrical insulation. This study provided a valuable idea for the design of thermal management materials for potential applications in integrated circuits. read less USED (low confidence) M. Zhou, T. Liang, B.-R. Wu, J. Liu, and P. Zhang, “Phonon transport in antisite-substituted hexagonal boron nitride nanosheets: A molecular dynamics study,” Journal of Applied Physics. 2020. link Times cited: 10 Abstract: This study uses non-equilibrium molecular dynamics simulatio… read moreAbstract: This study uses non-equilibrium molecular dynamics simulations to investigate the impact of antisite substitution on thermal conductivity. The phonon-dispersion curve and predicted thermal conductivity of pristine hexagonal boron nitride nanosheets (hBNNSs) show good agreement with the experiment results, indicating the reliability of the extep potential. It is clear that both neighboring substitution (NS) and random substitution (RS) drastically reduce the thermal conductivity of hBNNSs, of which RS has a larger effect. Calculations for the participation ratio and relaxation time show that the localization is the primary cause for the reduction in thermal conductivity when the defect concentration is low. When the defect concentration is higher, the primary cause is phonon-defect scattering in all phonon modes. RS has a larger effect on the phonon modes with long mean free paths, while NS has a larger effect on phonon modes with various lengths of mean free paths. read less USED (low confidence) B. Bagheri et al., “Correlation between surface topological defects and fracture mechanism of γ-graphyne-like boron nitride nanosheets,” Computational Materials Science. 2020. link Times cited: 18 USED (low confidence) T. Fang and Nguyen, “Atomistic wear mechanisms and deformation evolution in polishing.” 2020. link Times cited: 0 Abstract:
Our aim with this study was a new insight into the sub-nan… read moreAbstract:
Our aim with this study was a new insight into the sub-nanoscale of polishing and provides the atomic view of the material removal and wear mechanisms by carrying out molecule dynamics simulation. We proposed and analyzed a model with a diamond abrasive particle that sliding or rolling on the surface of GaN workpieces. The authors investigated, step by step, the effects of polishing depths, speeds, abrasive sizes, and crystalline orientations on the wear mechanisms and material removal. The wear mechanisms of the sliding motion were adhering, ploughing, and cutting, depending on the depths. While the wear mechanisms of rolling motion are adhering and ploughing. Notably, in both stages of sliding and rolling, there is an existence of a critical point at 5.0 Å depth when we considered the deformation behaviors. Below that critical point, the GaN workpiece will present an elastic deformation. From the aforementioned point, the workpiece would be plastically deformed. Besides, from 10 Å depth, the dislocation began to appear and evolute simultaneously with the development of the maximum shear stress. The sliding motion on the Ga-face could remove a greater number of atoms than that of the N-face. Moreover, direction [1-100] on Ga-face requesting more forces to polish than direction [11-20]. In conclusion, the main achievements that contribute to the field can be summarized as follows: the atomistic wear mechanisms of sliding and rolling motions, material removal, and the role of rolling motion at the sub-nanoscale during the ultrafine flat polishing process. read less USED (low confidence) B. Chava, Y. Wang, V. Sivasankar, and S. Das, “Water-free Localization of Anion at Anode for Small-Concentration Water-in-Salt Electrolytes Confined in Boron-Nitride Nanotube.” 2020. link Times cited: 3 USED (low confidence) Z. Z. He, Y. Zhu, and H. Wu, “Edge effect on interlayer shear in multilayer two-dimensional material assemblies,” International Journal of Solids and Structures. 2020. link Times cited: 6 USED (low confidence) A. Mayelifartash, M. A. Abdol, and S. Sadeghzadeh, “Mechanical properties of intrinsic and defective hybrid polyaniline (C3N)-BC3 nanosheets in the armchair and zigzag configurations: a molecular dynamics study,” Applied Physics A. 2020. link Times cited: 9 USED (low confidence) C. Ding, Y. Dai, F. Yang, and X. Chu, “A molecular dynamics study of the mechanical properties of the graphene/hexagonal boron nitride planar heterojunction for RRAM,” Materials today communications. 2020. link Times cited: 4 USED (low confidence) L. Fan and W. Yao, “Effect of transverse and longitudinal defects on mechanical properties of graphene-h-BN/copper vertically-stacked heterostructure,” Computational Materials Science. 2020. link Times cited: 11 USED (low confidence) X. Nie, L. Zhao, S. Deng, and X. Chen, “How interlayer twist angles affect thermal conduction of double-walled nanotubes: A non-equilibrium molecular dynamics study,” International Journal of Heat and Mass Transfer. 2020. link Times cited: 4 USED (low confidence) H. Ghasemi, B. Abraham, J. Rutledge, and H. Yazdani, “Mechanical properties of C3N nanotubes,” Diamond and Related Materials. 2020. link Times cited: 3 USED (low confidence) L. Fan, W. Yao, and Z. Zhang, “Regulation of failure mechanism of a bilayer Gr/h-BN staggered stacked heterostructure via interlayer sp3 bonds, interface connection, and defects,” Applied Physics A. 2020. link Times cited: 7 USED (low confidence) J. Song, Z. Xu, and X. He, “Thermal energy transport across the graphene/C3N interface,” International Journal of Heat and Mass Transfer. 2020. link Times cited: 11 USED (low confidence) A. Senturk, A. Oktem, and A. E. S. Konukman, “Thermal conductivity and mechanical properties of graphene-like BC2, BC3 and B4C3,” Molecular Simulation. 2020. link Times cited: 11 Abstract: ABSTRACT Recently, carbon-based 2D nanomaterials have receiv… read moreAbstract: ABSTRACT Recently, carbon-based 2D nanomaterials have received significant attention because of their superior physical properties. In this investigation, the thermal conductivity (TC) and mechanical properties of graphene-like BC2, BC3 and B4C3 structures are systematically examined, using molecular dynamics (MD) simulations. For graphene-like BC2, BC3 and B4C3 structures, our MD results predict remarkably high thermal and mechanical properties. Especially, graphene-like BC3 structure indicates higher mechanical properties than graphene-like BC2 and B4C3 structures. Also, the mechanical properties of these graphene-like structures are investigated at four various temperatures from 200 to 900 K. Our results indicate that the mechanical properties of graphene-like structures gradually decrease as the temperature rises. In addition, the failure processes of graphene-like BC2, BC3 and B4C3 structures are examined at room temperature. According to the MD simulations, these graphene-like structures show brittle failure mechanism. In addition, graphene-like BC3 structure is more stretchable than other structures. Remarkably, non-equilibrium MD simulation results demonstrate ultra high TC values of graphene-like BC2, BC3 and B4C3 structures and so propose them for thermal management of polymeric materials or in nanoelectronics. Similar to the mechanical properties, graphene-like BC3 has higher TC value than others. read less USED (low confidence) A. Senturk, “Outstanding thermo-mechanical properties of graphene-like B3C3 and C3N3,” Applied Physics A. 2020. link Times cited: 5 USED (low confidence) H. Ghasemi, J. Rutledge, and H. Yazdani, “Mechanical properties of defective cyanoethynyl (2D polyaniline – C3N): A comparative molecular dynamics study versus graphene and hexagonal boron nitride,” Physica E-low-dimensional Systems & Nanostructures. 2020. link Times cited: 4 USED (low confidence) A. Senturk, A. Oktem, and A. E. S. Konukman, “The influences of boron doping in various defect sites on the thermo-mechanical properties of armchair graphene nanoribbons,” The European Physical Journal B. 2020. link Times cited: 2 USED (low confidence) A. Bondarev, A. Fraile, T. Polcar, and D. Shtansky, “Mechanisms of friction and wear reduction by h-BN nanosheet and spherical W nanoparticle additives to base oil: Experimental study and molecular dynamics simulation,” Tribology International. 2020. link Times cited: 35 USED (low confidence) V.-T. Pham and T. Fang, “Anisotropic mechanical strength, negative Poisson’s ratio and fracture mechanism of borophene with defects,” Thin Solid Films. 2020. link Times cited: 16 USED (low confidence) T. Ma, C. T. Lin, and Y. Wang, “The dimensionality effect on phonon localization in graphene/hexagonal boron nitride superlattices,” 2D Materials. 2020. link Times cited: 11 Abstract: Phonon localization, a largely elusive phenomenon, has a gre… read moreAbstract: Phonon localization, a largely elusive phenomenon, has a great promise for improving current applications like thermoelectric materials and thermal barrier coatings. By freezing the out-of-plane atomic motion in graphene/hexagonal boron nitride (hBN) superlattices and random multilayers, i.e aperiodic superlattices, we are able to completely isolate the effect of the third dimension on phonon scattering and localization in 2D materials. In particular, we find much more prominent phonon heat conduction and localization when atomic motions in the third dimension are frozen. Rigorous spectral phonon transmission and scattering phase space analyses reveal that the phase-breaking anharmonic scatterings can significantly hinder the occurrence of phonon localization. Phonon participation ratio calculations further reveal that the flexural modes—arising from the degree of freedom of the third dimension—are rather extended, in contrast to the vastly localized in-plane modes in graphene/hBN random multilayers. These two factors altogether greatly obstruct the observation of coherent phonon localization in realistic materials. This work will be useful for guiding the search for nanostructures possessing significant phonon localization behaviors. read less USED (low confidence) M. Mehrabani, M. M. Khatibi, M. Ashory, and S. Sadeghzadeh, “Effect of nitrogen or boron impurities on the mechanical and vibrational properties of graphene nanosheets: a molecular dynamics approach,” Micro & Nano Letters. 2020. link Times cited: 0 Abstract: Investigation of mechanical and vibrational properties of na… read moreAbstract: Investigation of mechanical and vibrational properties of nano-structures using the analytical methods would be time-consuming. Therefore, using a semi-empirical method would reduce the time needed to investigate materials characterisation. One of the semi-empirical approaches is molecular dynamics. In this Letter, the large-scale atomic/molecular massively parallel simulator software is used to simulate the mechanical and vibrational behaviour of a nitrogen- and boron-doped 24.04 × 51.13 A graphene nano-sheet. The natural frequencies, Young's modulus, and ultimate tensile strength (UTS) are studied. By adding impurity to the nanosheet and increasing its density, Young's modulus, UTS, and natural frequencies were decreased. The decrease in tensile properties was more significant in the case of boron impurity. When the boron (nitrogen) impurity increased to about 20%, Young's modulus and the first natural frequency were decreased 7.1% (9%) and 16.8% (73%), respectively. This illustrates that Young's modulus and natural frequencies are directly related. Therefore, for the same dimensions and boundary conditions, it is obvious that the increase in impurity content has reduced the natural frequencies of the nanostructure. read less USED (low confidence) L. Seremetis et al., “Thermomechanical Response of Supported Hexagonal Boron Nitride Sheets of Various Thicknesses,” Journal of Physical Chemistry C. 2020. link Times cited: 5 Abstract: Raman spectroscopy is employed to investigate the temperatur… read moreAbstract: Raman spectroscopy is employed to investigate the temperature dependence of the E2g phonon mode of single-layer, few-layer (FL), and bulk hexagonal boron nitride (hBN) sheets, situated over Si/SiO2... read less USED (low confidence) A. Salmankhani, Z. Karami, A. H. Mashhadzadeh, M. Saeb, V. Fierro, and A. Celzard, “Mechanical Properties of C3N Nanotubes from Molecular Dynamics Simulation Studies,” Nanomaterials. 2020. link Times cited: 13 Abstract: Although the properties of carbon nanotubes (CNTs) are very … read moreAbstract: Although the properties of carbon nanotubes (CNTs) are very well-known and are still extensively studied, a thorough understanding of other carbon-based nanomaterials such as C3N nanotubes (C3NNTs) is still missing. In this article, we used molecular dynamics simulation to investigate the effects of parameters such as chirality, diameter, number of walls, and temperature on the mechanical properties of C3N nanotubes, C3N nanobuds, and C3NNTs with various kinds of defects. We also modeled and tested the corresponding CNTs to validate the results and understand how replacing one C atom of CNT by one N atom affects the properties. Our results demonstrate that the Young’s modulus of single-walled C3NNTs (SWC3NNTs) increased with diameter, irrespective of the chirality, and was higher in armchair SWC3NNTs than in zigzag ones, unlike double-walled C3NNTs. Besides, adding a second and then a third wall to SWC3NNTs significantly improved their properties. In contrast, the properties of C3N nanobuds produced by attaching an increasing number of C60 fullerenes gradually decreased. Moreover, considering C3NNTs with different types of defects revealed that two-atom vacancies resulted in the greatest reduction of all the properties studied, while Stone–Wales defects had the lowest effect on them. read less USED (low confidence) F. Momeni, B. Mehrafrooz, A. Montazeri, and A. Rajabpour, “MD-based design of bilayer graphene-hBN heterostructures: An insight into enhanced thermal transport,” International Journal of Heat and Mass Transfer. 2020. link Times cited: 13 USED (low confidence) L. Fan and W. Yao, “Effects of vacancy defects on the mechanical properties of graphene/hexagonal BN superlattice nanoribbons,” New Carbon Materials. 2020. link Times cited: 6 USED (low confidence) K. E. Eshkalak, S. Sadeghzadeh, and M. Jalaly, “Thermal resistance analysis of hybrid graphene-boron nitride nanosheets: The effect of geometry, temperature, size, strain and structural defects,” Computational Materials Science. 2020. link Times cited: 18 USED (low confidence) X. Zhang, J. Zhang, and M. Yang, “Molecular dynamics study on the thermal conductivity of bilayer graphene with nitrogen doping,” Solid State Communications. 2020. link Times cited: 8 USED (low confidence) B. Yang et al., “Molecular dynamic simulation of thermal transport in monolayer C3BxN1−x alloy,” Nanotechnology. 2020. link Times cited: 2 Abstract: Recently, two-dimensional (2D) monolayers C3B and C3N attrac… read moreAbstract: Recently, two-dimensional (2D) monolayers C3B and C3N attract growing research interest due to the excellent physical properties. In this work, the thermal conductivities (k) of the monolayer C3BxN1−x alloy and the special C3B0.5N0.5 superlattice (C3B0.5N0.5-SL) alloy are systematically evaluated by using molecular dynamic simulation. First, the k of monolayer C3BxN1−x alloy presents a U-shaped profile with the increasing random doping ratio (x), in which the lowest k exists in x = 0.5. Second, we further calculate the thermal conductivity of C3B0.5N0.5-SL. The result shows an initial decreasing and then rising trend, and the coherent length is 5.11 nm which occupies the minimum thermal conductivity. Furthermore, to uncover the phonon thermal transport mechanism, we calculate the spatiotemporal thermal transport, phonon density of states, phonon group velocity, participation ratio and the phonon wave packet simulations in monolayer alloy system. We note that on account of the random doping atoms, the enhancive phonon-impurity scattering and phonon localization reduce the thermal conductivity in monolayer C3BxN1−x alloy. In C3B0.5N0.5-SL, when the period length is smaller than the coherent length, coherent phonon modes emerge because of the phonon interference, in which the superlattice can be regarded as a ‘newly generated material’. However, when the period length is larger than the coherent length, the decreasing number of the interface in superlattice lessens phonon-interface scattering and cause the increasing thermal conductivity. This work contributes the fundamental knowledge for thermal management in 2D monolayer C3BxN1−x alloy based nanoelectronics. read less USED (low confidence) Y. Ni, H. Zhang, S. Hu, H. Wang, S. Volz, and S. Xiong, “Interface diffusion-induced phonon localization in two-dimensional lateral heterostructures,” International Journal of Heat and Mass Transfer. 2019. link Times cited: 15 USED (low confidence) R. Ravinder, P. Garg, and N. Krishnan, “Glass Transition and Crystallization in Hexagonal Boron Nitride: Crucial Role of Orientational Order,” Advanced Theory and Simulations. 2019. link Times cited: 1 Abstract: While extensive studies have been carried out on 2D crystals… read moreAbstract: While extensive studies have been carried out on 2D crystals, their disordered counterpart, namely 2D glasses, remain poorly explored. Using molecular dynamics simulation, it is demonstrated that hexagonal boron nitride (h‐BN) can exhibit crystallization and glass transition. Similar to archetypical glasses, it is observed that the glassy structures are disordered, marked by the absence of any long‐range order while exhibiting some short‐range order. Further, the structures obtained are stable in three dimensions, confirming the realistic nature of the 2D glasses. Interestingly, it is observed that the orientational order of the h‐BN structure with respect to density as well as ground state enthalpy follows a master curve for both crystallization and glass transition, revealing thermally accessible regions for the structure. Further, the standard deviation of orientational order provides information about the spatial heterogeneity in the structure, the rearrangement of which results in the formation of crystal/glass. This suggests that the orientational order may play a crucial role in controlling the propensity for crystallization/glass transition in systems having directional bonds. read less USED (low confidence) M. S. Elapolu, A. Tabarraei, A. Reihani, and A. Ramazani, “Phononic thermal transport properties of C3N nanotubes,” Nanotechnology. 2019. link Times cited: 13 Abstract: Reverse nonequilibrium molecular dynamics (RNEMD) is employe… read moreAbstract: Reverse nonequilibrium molecular dynamics (RNEMD) is employed to study the phononic thermal transport properties of C3N nanotubes. We study the effect of nanotube length and diameter on the thermal conductivity and investigate the phonon transport transition from ballistic to diffusive regime in C3N nanotubes. It is found that the thermal conductivity of C3N nanotubes is significantly lower than those of carbon nanotubes across the entire ballistic-diffusive range. In addition, significantly lower ballistic to diffusive transition length (72–80 nm) is observed in C3N nanotubes compared to carbon nanotubes. The inspection of phonon dispersion curves shows that carbon nanotubes have stiffer acoustic modes than C3N nanotubes which results in lower group velocities for C3N nanotubes. Due to the presence of nitrogen atoms, the phonon mean free paths and relaxation times of C3N nanotubes are shorter than those of the carbon nanotubes. The combined effect of lower group velocities and relaxation times leads to the lower thermal conductivity of C3N nanotubes. read less USED (low confidence) S. M. Hatam-Lee, A. Rajabpour, S. Volz, and S. Volz, “Thermal conductivity of graphene polymorphs and compounds: From C3N to graphdiyne lattices,” Carbon. 2019. link Times cited: 47 USED (low confidence) Y. Ren, Y. Wu, Z. Zong, X. Yang, B. Xiao, and K. Wu, “Heat Transfer in BNNT-Polymer Nanocomposites from Non-equilibrium Molecular Dynamics,” 2019 IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP). 2019. link Times cited: 0 Abstract: Doping high thermal conductivity fillers into polymers as a … read moreAbstract: Doping high thermal conductivity fillers into polymers as a major way to improve the thermal conductivity of materials, but the failure mechanism of the coupling agents and entangled polymer chains on the thermal conductivity of nanofillers is missing. In order to explore those, the thermal conductivity of pure BN nanotube and BN nanotube with coupling agents was calculated by the nonequilibrium molecular dynamics method. It is shown that the thermal conductivity of BN nanotube with coupling agents decreased significantly at the full frequency range. The dynamical structural factor was calculated to exact the longitudinal acoustics mode of BNNT in the nanocomposites and found that the entangled polyethylene chains have little effect on the thermal conductivity of BNNT and the coupling agents are the main factor to destroy the thermal conductivity. Based on those results, a new branches method is proposed that the coupling agent should bond at the edge not on the surface for single-wall BNNT. read less USED (low confidence) R. K. Zahedi, A. N. Shirazi, P. Alimouri, N. Alajlan, and T. Rabczuk, “Mechanical properties of graphene-like BC3; a molecular dynamics study,” Computational Materials Science. 2019. link Times cited: 32 USED (low confidence) L. Fan and W. Yao, “Regulation and coupling effects on mechanical properties of copper-graphene/h-BN layered heterostructure via ion irradiation, interlayer sp3 bonds and temperature,” Materials Research Express. 2019. link Times cited: 4 Abstract: In this paper, by using the molecular dynamics method, vario… read moreAbstract: In this paper, by using the molecular dynamics method, various defects have been created in graphene/h-BN with interlayer sp3 bonds (G/BN-sp3) by using ion irradiation. The copper-graphene/h-BN layered heterostructure (Cu-G/BN-sp3) were prepared by inserting G/BN-sp3 after irradiation damage into the single crystal copper matrix. The coupling effects of ion irradiation, interlayer sp3 bonds and temperature on defective copper-graphene/h-BN layered heterostructure were studied. The results show with the increase of ion irradiation doses, the mechanical properties of copper layered heterostructure decrease. When defects (caused by ion irradiation) and sp3 bonds coexist, if the defects are created around the sp3 bonds, the composite system is more vulnerable to damage. The location of the defects is an important factor to determine the crack position and fracture direction of copper layered heterostructure. Although ion irradiation and sp3 defects have adverse effects on mechanical properties, the mechanical properties of pure copper are still improved by introducing graphene/h-BN heterostructure. It provides a new way to enhance the radiation resistance and corrosion resistance of copper matrix composites. Meanwhile, controlling and strengthening the properties of copper matrix composites from a new perspective. read less USED (low confidence) L. Fan and W. Yao, “Effect of interlayer sp3 bonds and nanopores on mechanical properties of vertically-stacked 2D heterostructures,” Materials Research Express. 2019. link Times cited: 7 Abstract: A vertically-stacked 2D heterostructure is established, befo… read moreAbstract: A vertically-stacked 2D heterostructure is established, before the geometric nanopores (circular and square) and interlayer sp3 bonds are created in the vertically-stacked 2D heterostructures. By using molecular dynamics method, the Young’s modulus of defective vertically-stacked 2D heterostructures in different cases have been studied, including sizes and positions of nanopores, and different sp3 bonds fraction. The results show that the Young’s modulus of vertically-stacked 2D heterostructures decrease with the increase of nanopores size. In addition, when square nanopores are placed at different locations of vertically-stacked 2D heterostructures, Young’s modulus of vertically-stacked 2D heterostructures have changed greatly to do not follow the general tendency. The adverse effect of square nanopores on Young’s modulus of vertically-stacked 2D heterostructures is stronger than that of circular nanopores. When square nanopores and interlayer sp3 bonds coexist, the damage to heterostructures will be more significant, indicating that sp3 bonds can be considered as a special defect. It provides a way to regulate the performance of hybrid structures (choosing the appropriate geometric nanopores and interlayer sp3 bonds) according to the actual situation. In addition, it provides a reference for the application of nanopores in DNA detection. read less USED (low confidence) W. Yao and L. Fan, “Effect of defects on mechanical properties of novel hybrid graphene-h-BN/copper layered nanostructures,” Applied Physics A. 2019. link Times cited: 3 USED (low confidence) W. Qu, S. Bagchi, X. Chen, H. Chew, and C. Ke, “Bending and interlayer shear moduli of ultrathin boron nitride nanosheet,” Journal of Physics D: Applied Physics. 2019. link Times cited: 26 Abstract: We investigate the bending rigidity of ultrathin hexagonal b… read moreAbstract: We investigate the bending rigidity of ultrathin hexagonal boron nitride nanosheet (BNNS) through quantifying its self-folded conformations on flat substrates by using atomic force microscopy and atomistic simulations. The bending stiffness of two to six layers of BNNS is found to follow a power function of its thickness with a power index of ~2.35 and is substantially higher than that of comparable graphene. In contrast, monolayer graphene possesses a higher stiffness than its h-BN counterpart. We attribute the high bending stiffness of multilayer BNNS to its partially ionic B–N bondings and corrugated electronic structures, which result in one order of magnitude stronger interlayer shear interaction in h-BN than in graphene. The higher out-of-plane bending and interlayer shear rigidities suggest that unlike graphene, BNNS is less prone to interlayer delamination-induced structural inhomogeneities (e.g. shearing, rippling and kinks) and thus is suitable as a building block for atomically thin electronics and a reinforcing filler for nanocomposites. read less USED (low confidence) L. Fan and W. Yao, “Effect of defects on mechanical properties of planar h-BN-graphene heterostructure,” Materials Research Express. 2019. link Times cited: 8 Abstract: In this paper, a novel planar graphene/h-BN heterostructure … read moreAbstract: In this paper, a novel planar graphene/h-BN heterostructure (PG/h-BN) is established. The geometric defects were created in the novel planar graphene/h-BN heterostructure. The mechanical properties of PG/h-BN in the presence of geometric defects have been studied, and the effects of dimensions and positions of geometric defects on mechanical properties have also been investigated by using molecular dynamics method. The results show that mechanical properties of defective PG/h-BN decrease with the increase in the diameter of the geometric defects. Meanwhile, planar heterojunction with square nanoholes are more prone to stress concentration than planar heterojunction with circular nanoholes. In addition, in the presence of geometric defects, the failure strain and strength of planar heterojunction more affected by geometric defects, and the degree of influence is greater than Young’s modulus. It is very important for the defects to regulate the physical properties of planar heterojunctions. read less USED (low confidence) Y. Zhang, Q. Pei, Z. Sha, and Y.-W. Zhang, “A molecular dynamics study of the mechanical properties of h-BCN monolayer using a modified Tersoff interatomic potential,” Physics Letters A. 2019. link Times cited: 30 USED (low confidence) F. Mehralian, R. D. Firouz-Abadi, and M. Norouzi, “Molecular dynamics study on axial elastic modulus of carbon nanoropes,” Archives of Civil and Mechanical Engineering. 2019. link Times cited: 1 USED (low confidence) L. Fan and W. Yao, “Mechanical properties of a G/h-BN heterobilayer nanosheets coupled by interlayer sp3 bonds and defects,” Materials Research Express. 2019. link Times cited: 21 Abstract: The mechanical properties of graphene/hexagonal boron nitrid… read moreAbstract: The mechanical properties of graphene/hexagonal boron nitride (G/h-BN) heterobilayer nanosheets coupled by interlayer sp3 bonds and defects have been investigated by using the molecular dynamics (MD) simulation. For this purpose, interlayer sp3 bonds and two kinds of geometric imperfection (including rhombus and square nanopore) are formed in the G/h-BN heterobilayer nanosheets. The effects of adding the nanopore diameter, interlayer sp3 bonds fraction, and the influence of different position of geometric imperfection in heterobilayer nanostructure on mechanical properties have been investigated. The result shows that when sp3 bonds and nanopore coexist, the mechanical properties of defective graphene layer are higher than that of defective hexagonal boron nitride (h-BN) layer. Meanwhile, the negative effect of rhomboid nanohole on mechanical properties of heterostructure is weaker than that of square nanohole. It is observed that that interlayer sp3 bonds have greatest influence on the fracture strain of G/h-BN heterobilayer nanostructure, followed by fracture stress, and finally Young’s modulus. Another important point is that interlayer sp3 bonds can be regarded as a special defect, and its value seems to outweigh the intrinsic defects. read less USED (low confidence) M. Li et al., “Effect of Stone-Wales Defect on Mechanical Properties of Gr/epoxy Nanocomposites,” Polymers. 2019. link Times cited: 11 Abstract: Due to its superior mechanical properties, graphene (Gr) has… read moreAbstract: Due to its superior mechanical properties, graphene (Gr) has the potential to achieve high performance polymer-based nanocomposites. Previous studies have proved that defects in the Gr sheets could greatly reduce the mechanical properties of Gr, while the Stone-Wales (SW) defect was found to enhance the interfacial mechanical strength between Gr and epoxy. However, the combined effects of defects on the overall mechanical properties of Gr/epoxy nanocomposites have not been well understood. In this paper, the effect of the SW defect on the mechanical properties of Gr/epoxy nanocomposites was systematically investigated by using molecular dynamic simulations. The simulation results showed that the SW defect would degrade the mechanical properties of nanocomposites, including the Young’s modulus and in-plane shear modulus. Surprisingly, the transverse shear modulus could be remarkably enhanced with the existence of SW. The reinforcing mechanisms were mainly due to two aspects: (1) the SW defect could increase the surface roughness of the Gr, preventing the slippage between Gr and epoxy during the transverse shea; and (2) the nanocomposite with defective Gr enables a higher interaction energy than that with perfect graphene. Additionally, the effects of temperature, the dispersion and volume fraction of Gr were also investigated. read less USED (low confidence) S. Hu et al., “Disorder limits the coherent phonon transport in two-dimensional phononic crystal structures.,” Nanoscale. 2019. link Times cited: 43 Abstract: Recently, increasing efforts are being made to control therm… read moreAbstract: Recently, increasing efforts are being made to control thermal transport via coherent phonons in periodic phononic structures; however, the direct observation of coherent phonon transport is experimentally very difficult at ambient temperature, and the importance of coherent phonons to the total thermal conductivity has not been critically assessed to date. In this study, using the non-equilibrium molecular dynamics simulations, we studied coherent phonon transport in a C3N phononic crystal (CNPnC) structure at room temperature by changing the porosity. When the holes were randomly distributed to construct the disordered C3N (D-C3N) structure, the localization of the coherent phonons was revealed by the phonon transmission coefficient, phonon wave packet simulation, phonon participation ratio and spatial energy density, which led to a significant reduction in the thermal conductivity. Finally, the effects of the length, temperature and strain on the thermal conductivity of CNPnC and D-C3N have also been discussed. Our study provides a solid understanding of the coherent phonon transport behavior, which will be beneficial for phononic-related control based on coherent phonons. read less USED (low confidence) J. Song et al., “Thermal conductivity of two-dimensional BC3: a comparative study with two-dimensional C3N.,” Physical chemistry chemical physics : PCCP. 2019. link Times cited: 21 Abstract: The thermal conductivities of single-layer BC3 (SLBC) sheets… read moreAbstract: The thermal conductivities of single-layer BC3 (SLBC) sheets and their responses to environmental temperature, vacancy defects and external strain have been studied and compared with those of single-layer C3N (SLCN) sheets by molecular dynamics (MD) simulations. We found that SLBC and SLCN are isotropic in the basal plane and that their predicted thermal conductivities for infinite length sheets are 488.54 W m-1 K-1 and 799.87 W m-1 K-1, respectively. Despite many similar features in the structures of these materials, SLBC exhibits a lower thermal conductivity than SLCN due to stronger flexural acoustic phonon-defect scattering rates and weaker interatomic bonding stiffnesses. The vibrational density of states (VDOS) are calculated in both structures to elucidate their thermal conductivity differences. SLBC exhibits a more substantial redshift phenomenon in the high- and low-frequency domains than SLCN. In addition, the thermal conductivities of these materials exhibit decreasing trends in response to increases in temperature and defect ratio, and the temperature effect in SLBC is more substantial than that in SLCN, while the defect effect in SLBC is less substantial than that in SLCN. The influences of uniaxial compressive and tensile strains on the thermal conductivities of these materials are analysed separately. These two deformation modes cause different effects on the thermal transport behaviours of SLBC and SLCN: the effect of uniaxial compressive strain is slightly negative, while the effect of uniaxial tensile strain is initially positive and then negative. Moreover, the biaxial strains result in a more severe reduction in thermal conductivity than the uniaxial strains. Remarkably, the impact of uniaxial and biaxial tensile strains on thermal transport was stronger in SLBC than in SLCN. We propose that SLBC nanomembranes are promising candidates for various thermal applications. read less USED (low confidence) Z. Dai et al., “Mechanical responses of boron-doped monolayer graphene,” Carbon. 2019. link Times cited: 21 USED (low confidence) P. F. Achari, K. K. Bejagam, S. Singh, and S. A. Deshmukh, “Development of non-bonded interaction parameters between hexagonal boron-nitride and water,” Computational Materials Science. 2019. link Times cited: 8 USED (low confidence) X. Cheng and X. Wang, “Thermal transport in C3N nanotube: a comparative study with carbon nanotube,” Nanotechnology. 2019. link Times cited: 12 Abstract: One-dimensional nanotubes, such as carbon nanotube (CNT) and… read moreAbstract: One-dimensional nanotubes, such as carbon nanotube (CNT) and C3N nanotube (C3NNT), are attracting growing research interest due to their excellent electrical and thermal properties. In this work, the thermal transport of a single-walled C3NNT is investigated in comparison with a single-walled CNT using classical molecular dynamic simulations. We firstly observe that the thermal conductivity (k) of C3NNT is lower than that of CNT. Due to the phonon scattering in the N atoms of C3NNT, the energy is localized around the N atoms. Monotonic decreasing trends of k with increasing temperature are shown in CNT and C3NNT, indicating strong Umklapp phonon scattering. Afterwards, uniaxial strains from −10% to 14% are applied to the nanotubes, and the thermal conductivity initially increases and then decreases. Phonon density of states, phonon dispersions, participation ratios, and spatial distribution of energy are used to analyze the phonon behaviors in nanotubes. This work provides fundamental thermo-physical knowledge to the thermal management of CNT and C3NNT based nanoelectronics. read less USED (low confidence) V. Vijayaraghavan and L. Zhang, “Nanomechanics of single layer hybrid boron nitride–carbon nanosheets: A molecular dynamics study,” Computational Materials Science. 2019. link Times cited: 12 USED (low confidence) A. Kipper and L. B. D. Silva, “Non equilibrium molecular dynamics simulation study of thermal conductivity in doped graphene nanoribbons,” Physica B: Condensed Matter. 2019. link Times cited: 8 USED (low confidence) H. Loulijat, A. Koumina, and H. Zerradi, “The effect of the thermal vibration of graphene nanosheets on viscosity of nanofluid liquid argon containing graphene nanosheets,” Journal of Molecular Liquids. 2019. link Times cited: 10 USED (low confidence) S. Sadeghzadeh, “Wrinkling C3N nano-grids in uniaxial tensile testing; a molecular dynamics study,” Diamond and Related Materials. 2019. link Times cited: 9 USED (low confidence) T. Liang, P. Zhang, P. Yuan, S. Zhai, and D. Yang, “A molecular dynamics study on the thermal conductivities of single- and multi-layer two-dimensional borophene,” Nano Futures. 2019. link Times cited: 23 Abstract: Borophene, a new two-dimensional (2D) structure of boron ato… read moreAbstract: Borophene, a new two-dimensional (2D) structure of boron atoms, has aroused a great deal of attention and research recently. However, research on the thermal conductivity of borophene is still scarce, although this is critical for the potential application of borophene. Accordingly, we investigate the in-plane and cross-plane thermal conductivities of single- and multi-layer borophene using the non-equilibrium molecular dynamics simulations. The effect on the thermal conductivity with respect to sample length, temperature, layer number and mechanical strain is systematically examined. It is found that the in-plane thermal conductivity of infinite-size single-layer borophene exhibits strong anisotropy, which is calculated to be 102.5 ± 1.9 (along the zigzag direction) and 233.3 ± 2.1 W m−1K−1 (along the armchair direction). Notably, we found that both the in-plane and cross-plane thermal conductivities of borophene are affected by temperature variations, which is the same as other 2D materials. Surprisingly, the in-plane thermal conductivity of multi-layer borophene is insensitive to the layer number. This is attributed to the out-of-plane flexural phonons mode vibration being maintained by the intrinsic bi-layer structure (buckled structure), resulting in a negligible effect of interlayer vdW interactions of the multi-layer structure on the out-of-plane flexural phonons mode. In particular, the cross-plane strain was found to be effective in modulating the cross-plane thermal conductivity of multi-layer borophene in our research. Our findings here are of significance for understanding the thermal transport behavior of single- and multi-layer borophene and promoting their future applications in thermal management and nanodevices. read less USED (low confidence) G. C. Loh, “Fast water desalination by carbon-doped boron nitride monolayer: transport assisted by water clustering at pores,” Nanotechnology. 2018. link Times cited: 6 Abstract: The well-being of the ever-escalating world population hinge… read moreAbstract: The well-being of the ever-escalating world population hinges largely upon the adequacy of clean, fresh water. Desalination is one of the most promising approaches in such an endeavor. Using molecular dynamics simulations, we take a close look at nanoporous hexagonal boron nitride nanosheets as desalination membranes, and study how C dopants affect their performance. The calculations predict that the desalination performance of C-doped BN membranes compares favorably to that of MoS2 membranes: the water flux through the 0% (0CB–0CN), 25% (3CB–0CN), 75% (3CB–6CN), and 100% C terminated BN membrane (6CB–6CN) is 29.9, 47.5, 95.3, and 81.5 molecules ns−1 per pore, respectively, and there is a strong correlation between the water flux and the axial diffusion coefficient. Through our study of the effect of C content on the desalination performance, it is found that more clustering of water molecules at membrane pores due to a smaller hydration free energy and pore energy barrier assists water transport through the pores, and allows a greater water flux. read less USED (low confidence) M. Dewapriya and R. Rajapakse, “Atomistic and continuum modelling of stress field at an inhomogeneity in graphene,” Materials & Design. 2018. link Times cited: 7 USED (low confidence) J. Yi, L. Wang, and Y. Zhang, “Vibration of two-dimensional hexagonal boron nitride,” Theoretical and Applied Mechanics Letters. 2018. link Times cited: 3 USED (low confidence) Q. Ding, N. Ding, L. Liu, N. Li, and C. M. L. Wu, “Investigation on mechanical performances of grain boundaries in hexagonal boron nitride sheets,” International Journal of Mechanical Sciences. 2018. link Times cited: 17 USED (low confidence) H. Zhang and B. Zhang, “Fast crack kinking manipulated by atomic hoop stress in monolayer hexagonal boron nitride strip,” Computational Materials Science. 2018. link Times cited: 5 USED (low confidence) K. E. Eshkalak, S. Sadeghzadeh, and M. Jalaly, “Studying the effects of longitudinal and transverse defects on the failure of hybrid graphene-boron nitride sheets: A molecular dynamics simulation,” Physica E: Low-dimensional Systems and Nanostructures. 2018. link Times cited: 26 USED (low confidence) S. Sadeghzadeh, “Effects of vacancies and divacancies on the failure of C3N nanosheets,” Diamond and Related Materials. 2018. link Times cited: 31 USED (low confidence) X.-K. Chen, J. Liu, Z.-X. Xie, Y. Zhang, Y.-xiang Deng, and K. Chen, “A local resonance mechanism for thermal rectification in pristine/branched graphene nanoribbon junctions,” Applied Physics Letters. 2018. link Times cited: 67 Abstract: Using non-equilibrium molecular dynamics simulations, we inv… read moreAbstract: Using non-equilibrium molecular dynamics simulations, we investigate thermal rectification (TR) in pristine/branched graphene nanoribbon (GNR) junctions. The results indicate that the TR ratio of such junctions can reach 470% under small temperature bias, which has distinct superiority over asymmetric GNR and many other junctions. Moreover, the TR ratio decreases rapidly as the applied temperature bias increases. It seems to be against common sense that the TR ratio generally increases with temperature bias. Phonon spectra analyses reveal that the observed phenomena stem from the local resonance of longitudinal phonons in branched GNR region under negative temperature bias. Furthermore, the influence of ambient temperature, system length, branch number, and defect density is studied to obtain the optimum conditions for TR. This work extends local resonance mechanism to GNR for thermal signal manipulation.Using non-equilibrium molecular dynamics simulations, we investigate thermal rectification (TR) in pristine/branched graphene nanoribbon (GNR) junctions. The results indicate that the TR ratio of such junctions can reach 470% under small temperature bias, which has distinct superiority over asymmetric GNR and many other junctions. Moreover, the TR ratio decreases rapidly as the applied temperature bias increases. It seems to be against common sense that the TR ratio generally increases with temperature bias. Phonon spectra analyses reveal that the observed phenomena stem from the local resonance of longitudinal phonons in branched GNR region under negative temperature bias. Furthermore, the influence of ambient temperature, system length, branch number, and defect density is studied to obtain the optimum conditions for TR. This work extends local resonance mechanism to GNR for thermal signal manipulation. read less USED (low confidence) M. Ge and C. Si, “Mechanical and electronic properties of lateral graphene and hexagonal boron nitride heterostructures,” Carbon. 2018. link Times cited: 14 USED (low confidence) S. Bazrafshan and A. Rajabpour, “Engineering of thermal transport in graphene using grain size, strain, nitrogen and boron doping; a multiscale modeling,” International Journal of Heat and Mass Transfer. 2018. link Times cited: 31 USED (low confidence) R. Rezaei, “Tensile mechanical characteristics and deformation mechanism of metal-graphene nanolayered composites,” Computational Materials Science. 2018. link Times cited: 39 USED (low confidence) Y. Dong, M. Meng, M. M. Groves, C. Zhang, and J. Lin, “Thermal conductivities of two-dimensional graphitic carbon nitrides by molecule dynamics simulation,” International Journal of Heat and Mass Transfer. 2018. link Times cited: 50 USED (low confidence) M. Wang et al., “Impact of interface types on spin transport in heterostructures of graphene/hexagonal boron-nitride nanoribbons,” Organic Electronics. 2018. link Times cited: 5 USED (low confidence) R. Kayser and A. Adnan, “Grain boundary driven mechanical properties of ZrB2 and ZrC‐ZrB2 nanocomposite: A molecular simulation study,” Journal of the American Ceramic Society. 2018. link Times cited: 10 USED (low confidence) C. Androulidakis, E. Koukaras, M. Poss, K. Papagelis, C. Galiotis, and S. Tawfick, “Strained hexagonal boron nitride: Phonon shift and Grüneisen parameter,” Physical Review B. 2018. link Times cited: 40 USED (low confidence) H.-T. Nguyen, M.-Q. Le, and V. Nguyen, “Mode-I stress intensity factors of silicene, AlN, and SiC hexagonal sheets,” Materials Research Express. 2018. link Times cited: 11 Abstract: The crack-tip displacement field and molecular dynamics fini… read moreAbstract: The crack-tip displacement field and molecular dynamics finite element method with Tersoff potentials were used to find the mode-I stress intensity factors (SIF) of silicene, aluminum nitride (AlN), and silicon carbide (SiC) hexagonal sheets. Fracture properties of graphene and boronitrene are also included for comparison. It is found that KIct (KIc is mode-I critical SIF and t is the sheet’s thickness) of silicene, AlN, and SiC sheets are approximately 80, 66, and 47%; and 73, 64, and 45% smaller values of those of graphene for crack along the armchair and zigzag directions, respectively. The estimated fracture toughness of silicene is close to the experimental data of single-crystal silicon. read less USED (low confidence) J. Wang et al., “The thermal and thermoelectric properties of in-plane C-BN hybrid structures and graphene/h-BN van der Waals heterostructures,” Materials Today Physics. 2018. link Times cited: 73 USED (low confidence) M. Dewapriya, S. Meguid, and R. Rajapakse, “Atomistic modelling of crack-inclusion interaction in graphene,” Engineering Fracture Mechanics. 2018. link Times cited: 13 USED (low confidence) K. Firestein et al., “Compressive properties of hollow BN nanoparticles: theoretical modeling and testing using a high-resolution transmission electron microscope.,” Nanoscale. 2018. link Times cited: 6 Abstract: Due to their excellent mechanical properties, nanoparticles … read moreAbstract: Due to their excellent mechanical properties, nanoparticles have great potential as reinforcing phases in composite materials, friction modifiers in liquid lubricants, catalysts and drug-delivery agents. In the present study, the mechanical analysis of individual spherical hollow BN nanoparticles (BNNPs) using a combination of in situ compression tests inside a high-resolution transmission electron microscope (TEM) and theoretical modelling was conducted. It was found that BNNPs display high mechanical stiffness and a large value of elastic recovery. This enables the hollow BNNPs to exhibit considerably large cyclic deformation (up to 30% of the sphere's original external diameter) and to accumulate plastic deformation of approximately 30% of the total compression strain. Theoretical simulations allowed for elucidation of BNNPs' structural changes under compression at the atomic level and explained the origin of their high stiffness and large critical deformation values. read less USED (low confidence) C. Si et al., “A comprehensive analysis about thermal conductivity of multi-layer graphene with N-doping, -CH3 group, and single vacancy,” Journal of Applied Physics. 2018. link Times cited: 11 Abstract: Graphene has received great attention due to its fascinating… read moreAbstract: Graphene has received great attention due to its fascinating thermal properties. The inevitable defects in graphene, such as single vacancy, doping, and functional group, greatly affect the thermal conductivity. The sole effect of these defects on the thermal conductivity has been widely studied, while the mechanisms of the coupling effects are still open. We studied the combined effect of defects with N-doping, the -CH3 group, and single vacancy on the thermal conductivity of multi-layer graphene at various temperatures using equilibrium molecular dynamics with the Green-Kubo theory. The Taguchi orthogonal algorithm is used to evaluate the sensitivity of N-doping, the -CH3 group, and single vacancy. Sole factor analysis shows that the effect of single vacancy on thermal conductivity is always the strongest at 300 K, 700 K, and 1500 K. However, for the graphene with three defects, the single vacancy defect only plays a significant role in the thermal conductivity modification at 300 K and 700 K, while the -CH3 group dominates the thermal conductivity reduction at 1500 K. The phonon dispersion is calculated using a spectral energy density approach to explain such a temperature dependence. The combined effect of the three defects further decreases the thermal conductivity compared to any sole defect at both 300 K and 700 K. The weaker single vacancy effect is due to the stronger Umklapp scattering at 1500 K, at which the combined effect seriously covers almost all the energy gaps in the phonon dispersion relation, significantly reducing the phonon lifetimes. Therefore, the temperature dependence only appears on the multi-layer graphene with combined defects.Graphene has received great attention due to its fascinating thermal properties. The inevitable defects in graphene, such as single vacancy, doping, and functional group, greatly affect the thermal conductivity. The sole effect of these defects on the thermal conductivity has been widely studied, while the mechanisms of the coupling effects are still open. We studied the combined effect of defects with N-doping, the -CH3 group, and single vacancy on the thermal conductivity of multi-layer graphene at various temperatures using equilibrium molecular dynamics with the Green-Kubo theory. The Taguchi orthogonal algorithm is used to evaluate the sensitivity of N-doping, the -CH3 group, and single vacancy. Sole factor analysis shows that the effect of single vacancy on thermal conductivity is always the strongest at 300 K, 700 K, and 1500 K. However, for the graphene with three defects, the single vacancy defect only plays a significant role in the thermal conductivity modification at 300 K and 700 K, while the... read less USED (low confidence) T. Li, Z. Tang, Z. Huang, and J. Yu, “Substrate effects on the thermal performance of in-plane graphene/hexagonal boron nitride heterostructures,” Carbon. 2018. link Times cited: 27 USED (low confidence) M. S. Elapolu and A. Tabarraei, “Kapitza conductance of symmetric tilt grain boundaries of monolayer boron nitride,” Computational Materials Science. 2018. link Times cited: 10 USED (low confidence) Y. Li, A. Wei, H. Ye, and H. Yao, “Correction: Mechanical and thermal properties of grain boundary in a planar heterostructure of graphene and hexagonal boron nitride.,” Nanoscale. 2018. link Times cited: 17 Abstract: Correction for 'Mechanical and thermal properties of gr… read moreAbstract: Correction for 'Mechanical and thermal properties of grain boundary in a planar heterostructure of graphene and hexagonal boron nitride' by Yinfeng Li, et al., Nanoscale, 2018, DOI: 10.1039/c7nr07306b. read less USED (low confidence) I. M. Felix and L. Pereira, “Thermal Conductivity of Graphene-hBN Superlattice Ribbons,” Scientific Reports. 2018. link Times cited: 70 USED (low confidence) K. Cai, L. Yang, J. Shi, and Q. Qin, “Critical conditions for escape of a high-speed fullerene from a BNC nanobeam after collision,” Scientific Reports. 2018. link Times cited: 9 USED (low confidence) L. Nan, N. Ding, S. Qu, L. Liu, W. Guo, and C. M. L. Wu, “Mechanical properties and failure behavior of hexagonal boron nitride sheets with nano-cracks,” Computational Materials Science. 2017. link Times cited: 32 USED (low confidence) G. Wang et al., “Interlayer Coupling Behaviors of Boron Doped Multilayer Graphene,” Journal of Physical Chemistry C. 2017. link Times cited: 26 Abstract: It is fundamentally important to understand how the interlay… read moreAbstract: It is fundamentally important to understand how the interlayer interaction of neighboring graphene sheets is influenced by chemical doping. Here we investigate the interlayer coupling of multilayer graphene doped with controlled boron content via the Raman-active in-plane shear mode. The experimental results reveal a remarkable decline in the interlayer shear modulus as boron content increases, which is a direct consequence of the enlarged interlayer spacing, further supported by the molecular dynamic (MD) simulations. Nanoindentation tests were conducted to clarify the influence of interlayer coupling behaviors on nanomechanical behaviors of boron-doped bilayer graphene. As the interlayer slippage is induced under shear deformations, the weakened shear resistance would lead to the reduced energy dissipation during sliding process. Our results provide valuable insight into fundamental mechanical properties of boron-doped graphene and its interfaces and potentially allows tailoring of interlayer coupling f... read less USED (low confidence) S. Thomas, K. Ajith, and M. C. Valsakumar, “Effect of ripples on the finite temperature elastic properties of hexagonal boron nitride using strain-fluctuation method,” Superlattices and Microstructures. 2017. link Times cited: 10 USED (low confidence) M. Hammad et al., “Adhesionless and near-ideal contact behavior of graphene on Cu thin film,” Carbon. 2017. link Times cited: 16 USED (low confidence) X. Wang, M. Wang, Y. Hong, Z. Wang, and J. Zhang, “Coherent and incoherent phonon transport in a graphene and nitrogenated holey graphene superlattice.,” Physical chemistry chemical physics : PCCP. 2017. link Times cited: 30 Abstract: The transition between coherent and incoherent phonon transp… read moreAbstract: The transition between coherent and incoherent phonon transport in a graphene (GRA) and nitrogenated holey graphene (C2N) superlattice is investigated by non-equilibrium molecular dynamics (NEMD) simulation. We find that the thermal conductivity of the GRA-C2N superlattice is much lower than those of graphene and C2N, and exhibits a positive correlation with the system length. Owing to three mechanisms, i.e., phonon wave interference, phonon confinement and phonon interface scattering, the calculated thermal conductivity shows a decreasing trend at small period length scales and gradually increases at large period length scales. The coherence length of the superlattice at 300 K is 4.43 nm, which is independent of the total length. In addition, the effects of temperature and uniaxial tensile strain on phonon transport are investigated. At 100 K, the coherent phonons play a more dominating role in the superlattice and the responding coherence length is enlarged to 7.38 nm. On the other hand, tensile strain can effectively reduce the thermal conductivity, which results from the phonon softening. read less USED (low confidence) A. Mehri, M. Jamaati, and A. Namiranian, “Electron transport in graphene/h-BN lateral hybrids: Rhombus and bowtie domains,” Superlattices and Microstructures. 2017. link Times cited: 7 USED (low confidence) C. Lin, X. Zhang, and Z. Rao, “Theoretical prediction of thermal transport in BC2N monolayer,” Nano Energy. 2017. link Times cited: 39 USED (low confidence) F. Gayk, J. Ehrens, T. Heitmann, P. Vorndamme, A. Mrugalla, and J. Schnack, “Young’s moduli of carbon materials investigated by various classical molecular dynamics schemes,” Physica E-low-dimensional Systems & Nanostructures. 2017. link Times cited: 16 USED (low confidence) S. Thomas, K. Ajith, and M. C. Valsakumar, “Empirical potential influence and effect of temperature on the mechanical properties of pristine and defective hexagonal boron nitride,” Materials Research Express. 2017. link Times cited: 11 Abstract: The major objective of this work is to present results of a … read moreAbstract: The major objective of this work is to present results of a classical molecular dynamics study to investigate the effect of changing the cut-off distance in the empirical potential on the stress–strain relation and also the temperature dependent Young’s modulus of pristine and defective hexagonal boron nitride. As the temperature increases, the computed Young’s modulus shows a significant decrease along both the armchair and zigzag directions. The computed Young’s modulus shows a trend in keeping with the structural anisotropy of h-BN. The variation of Young’s modulus with system size is elucidated. The observed mechanical strength of h-BN is significantly affected by the vacancy and Stone–Wales type defects. The computed room temperature Young’s modulus of pristine h-BN is 755 GPa and 769 GPa respectively along the armchair and zigzag directions. The decrease of Young’s modulus with increase in temperature has been analyzed and the results show that the system with zigzag edge shows a higher value of Young’s modulus in comparison to that with armchair edge. As the temperature increases, the computed stiffness decreases and the system with zigzag edge possesses a higher value of stiffness as compared to the armchair counterpart and this behaviour is consistent with the variation of Young’s modulus. The defect analysis shows that presence of vacancy type defects leads to a higher Young’s modulus, in the studied range with different percentage of defect concentration, in comparison with Stone–Wales defect. The variations in the peak position of the computed radial distribution function reveals the changes in the structural features of systems with zigzag and armchair edges in the presence of applied stress. read less USED (low confidence) X. Wang, Y. Hong, D. Ma, and J. Zhang, “Molecular dynamics study of thermal transport in a nitrogenated holey graphene bilayer,” Journal of Materials Chemistry C. 2017. link Times cited: 31 Abstract: Recent studies of graphene have spurred enormous interest in… read moreAbstract: Recent studies of graphene have spurred enormous interest in the exploration of novel 2D materials. Much attention has been paid to the opening of a direct bandgap in graphene, which enables its applications in field effect transistors (FET). Lately, a nitrogenated holey graphene structure with C2N stoichiometry has been synthesized, which exhibits extraordinary electrical properties. Heat dissipation plays a vital role in practical applications, and therefore its thermal properties need to be explored urgently. In this work, the basal-plane thermal conductivity (κ) and cross-plane interfacial thermal resistance (R) in a C2N bilayer structure are systematically investigated using the molecular dynamics (MD) method. The effects of several internal and external modulators, such as system temperature, longitudinal length, interlayer coupling strength and tensile strain on the calculated κ and R values are studied. The predicted κ for an infinite-length C2N bilayer is 80.0 W m−1 K−1 and the cross-plane R between C2N monolayers equals 3.4 × 10−8 K m2 W−1. The calculated thermal conductivities are found to decrease monotonically with temperature and tensile strain, while show negligible changes with coupling strength. On the other hand, both temperature and coupling strength can effectively reduce the interfacial thermal resistance with maximum R reductions amounting to 51% and 54%, respectively. read less USED (low confidence) R. Guerra, M. V. van Wijk, A. Vanossi, A. Fasolino, and E. Tosatti, “Graphene on h-BN: to align or not to align?,” Nanoscale. 2017. link Times cited: 14 Abstract: The contact strength, adhesion and friction, between graphen… read moreAbstract: The contact strength, adhesion and friction, between graphene and an incommensurate crystalline substrate such as h-BN depends on their relative alignment angle θ. The well-established Novaco-McTague (NM) theory predicts for a monolayer graphene on a hard bulk h-BN crystal face a small spontaneous misalignment, here θNM ≃ 0.45 degrees which if realized would be relevant to a host of electronic properties besides the mechanical ones. Because experimental equilibrium is hard to achieve, we inquire theoretically about alignment or misalignment by simulations based on dependable state-of-the-art interatomic force fields. Surprisingly at first, we find compelling evidence for θ = 0, i.e., full energy-driven alignment in the equilibrium state of graphene on h-BN. Two factors drive this deviation from the NM theory. First, graphene is not flat, developing on h-BN a long-wavelength out-of-plane corrugation. Second, h-BN is not hard, releasing its contact stress by planar contractions/expansions that accompany the interface moiré structure. Repeated simulations by artificially forcing graphene to keep flat, and h-BN to keep rigid, indeed yield an equilibrium misalignment similar to θNM as expected. Subsequent sliding simulations show that friction of graphene on h-BN, small and essentially independent of misalignments in the artificial frozen state, strongly increases in the more realistic corrugated, strain-modulated, aligned state. read less USED (low confidence) H. Badjian and A. Setoodeh, “Improved tensile and buckling behavior of defected carbon nanotubes utilizing boron nitride coating - A molecular dynamic study,” Physica B-condensed Matter. 2017. link Times cited: 22 USED (low confidence) J. Zhang, X. Wang, Y. Hong, Q. Xiong, J. Jiang, and Y. Yue, “Understanding thermal transport in asymmetric layer hexagonal boron nitride heterostructure,” Nanotechnology. 2017. link Times cited: 21 Abstract: In this work, thermal transport at the junction of an asymme… read moreAbstract: In this work, thermal transport at the junction of an asymmetric layer hexagonal boron-nitride (h-BN) heterostructure is explored using a non-equilibrium molecular dynamics method. A thermal contact resistance of 3.6 × 10−11 K · m2 W−1 is characterized at a temperature of 300 K with heat flux from the trilayer to monolayer regions. The mismatch in the flexural phonon modes revealed by power spectra analysis provides the driving force for the calculated thermal resistance. A high thermal rectification efficiency of 360% is calculated at the layer junction surpassing that of graphene. Several modulators, i.e. the system temperature, contact pressure and lateral dimensions, are applied to manipulate the thermal conductance and rectification across the interfaces. The predicted thermal rectification sustains positive correlations with temperature and phonon propagation lengths with little change to the coupling strength. read less USED (low confidence) T. Zhang and L. Zhu, “Giant reduction of thermal conductivity in a two-dimensional nitrogenated holey C2N nanosheet.,” Physical chemistry chemical physics : PCCP. 2017. link Times cited: 22 Abstract: Thermal conductivities of monolayer holey C2N nanosheets are… read moreAbstract: Thermal conductivities of monolayer holey C2N nanosheets are investigated via equilibrium molecular dynamics simulations. As compared with graphene, the lattice thermal conductivities of C2N decrease by two orders in magnitude, which are around 40 W m-1 K-1 at 300 K along both zigzag and armchair directions. The lattice dynamics calculations reveal that the reduced group velocities and shortened phonon lifetimes, due to the incorporation of nitrogen atoms and the holey structure, account for such a giant reduction in thermal conductivity. Our study also indicates that pyridinic-like nitrogen doping would be a more efficient way than graphite-like nitrogen doping to suppress the thermal conductivity of graphene. read less USED (low confidence) R. D’Souza and S. Mukherjee, “First principles calculation of thermoelectric parameters of Monolayer- and Bilayer-Graphene and Heterostructures of Graphene and h-BN,” Journal of Physics: Conference Series. 2016. link Times cited: 4 Abstract: Electrical conductivity and Seebeck coefficient were calcula… read moreAbstract: Electrical conductivity and Seebeck coefficient were calculated using Boltzmann transport theory based on first-principles bandstructure calculations for the monolayer- and bilayer-graphene. We also present calculations of the thermoelectric parameters of Graphene/h- BN/Graphene sandwiched heterostructures. These results will be discussed in the light of existing experimental data. read less USED (low confidence) Y. Zhao et al., “Molecular dynamics simulation of nano-indentation of (111) cubic boron nitride with optimized Tersoff potential,” Applied Surface Science. 2016. link Times cited: 25 USED (low confidence) Y. Hong, J. Zhang, and X. Zeng, “Thermal contact resistance across a linear heterojunction within a hybrid graphene/hexagonal boron nitride sheet.,” Physical chemistry chemical physics : PCCP. 2016. link Times cited: 41 Abstract: Interfacial thermal conductance plays a vital role in defini… read moreAbstract: Interfacial thermal conductance plays a vital role in defining the thermal properties of nanostructured materials in which heat transfer is predominantly phonon mediated. In this work, the thermal contact resistance (R) of a linear heterojunction within a hybrid graphene/hexagonal boron nitride (h-BN) sheet is characterized using non-equilibrium molecular dynamics (NEMD) simulations. The effects of system dimension, heat flux direction, temperature and tensile strain on the predicted R values are investigated. The spatiotemporal evolution of thermal energies from the graphene to the h-BN sheet reveals that the main energy carrier in graphene is the flexural phonon (ZA) mode, which also has the most energy transmissions across the interface. The calculated R decreases monotonically from 5.2 × 10(-10) to 2.2 × 10(-10) K m(2) W(-1) with system lengths ranging from 20 to 100 nm. For a 40 nm length hybrid system, the calculated R decreases by 42% from 4.1 × 10(-10) to 2.4 × 10(-10) K m(2) W(-1) when the system temperature increases from 200 K to 600 K. The study of the strain effect shows that the thermal contact resistance R between h-BN and graphene sheets increases with the tensile strain. Detailed phonon density of states (PDOS) is computed to understand the thermal resistance results. read less USED (low confidence) J. Zhang, W. Xie, X. Xu, S. Zhang, and J. Zhao, “Structural and Electronic Properties of Interfaces in Graphene and Hexagonal Boron Nitride Lateral Heterostructures,” Chemistry of Materials. 2016. link Times cited: 55 Abstract: The in-plane heterostructures composed of graphene and hexag… read moreAbstract: The in-plane heterostructures composed of graphene and hexagonal boron nitride (G/BN), as the first kind of two-dimensional metal/semiconductor heterostructures of one-atom thickness, are attractive for both fundamental low-dimensional physics and nanoscale devices because of the tailorable electronic properties. The atomic structures and electronic properties of interfaces in lateral G/BN heterostructures are investigated by first-principles calculations. The symmetric armchair interfaces have a similar formation energy but a larger band gap compared with the nonsymmetric interfaces. G/BN heterostructures with zigzag-type interfaces constructed under the guide of Clar’s rule are found to possess a lower formation energy than those with abrupt interfaces and open a finite band gap. In addition to the zigzag and armchair interfaces, other misorientated interfaces with pentagon and heptagon rings are also stable with low formation energies of 4.4–6.8 eV/nm. These theoretical results are important to clarify... read less USED (low confidence) X.-K. Chen, Z.-X. Xie, W.-X. Zhou, L.-M. Tang, and K. Chen, “Phonon wave interference in graphene and boron nitride superlattice,” Applied Physics Letters. 2016. link Times cited: 92 Abstract: The thermal transport properties of the graphene and boron n… read moreAbstract: The thermal transport properties of the graphene and boron nitride superlattice (CBNSL) are investigated via nonequilibrium molecular dynamics simulations. The simulation results show that a minimum lattice thermal conductivity can be achieved by changing the period length of the superlattice. Additionally, it is found that the period length at the minimum shifts to lower values at higher temperatures, and that the depth of the minimum increases with decreasing temperature. In particular, at 200 K, the thermal conductivities of CBNSLs with certain specific period lengths are nearly equal to the corresponding values at 300 K. A detailed analysis of the phonon spectra shows that this anomalous thermal conductivity behavior is a result of strong phonon wave interference. These observations indicate a promising strategy for manipulation of thermal transport in superlattices. read less USED (low confidence) R. Rezaei, M. Shariati, H. Tavakoli-Anbaran, and C. Deng, “Mechanical characteristics of CNT-reinforced metallic glass nanocomposites by molecular dynamics simulations,” Computational Materials Science. 2016. link Times cited: 45 USED (low confidence) K. Firestein et al., “Structural analysis and atomic simulation of Ag/BN nanoparticle hybrids obtained by Ag ion implantation.” 2016. link Times cited: 19 USED (low confidence) A. Tabarraei and X. Wang, “Anomalous thermal conductivity of monolayer boron nitride,” Applied Physics Letters. 2016. link Times cited: 31 Abstract: In this paper, we use nonequilibrium molecular dynamics mode… read moreAbstract: In this paper, we use nonequilibrium molecular dynamics modeling to investigate the thermal properties of monolayer hexagonal boron nitride nanoribbons under uniaxial strain along their longitudinal axis. Our simulations predict that hexagonal boron nitride shows an anomalous thermal response to the applied uniaxial strain. Contrary to three dimensional materials, under uniaxial stretching, the thermal conductivity of boron nitride nanoribbons first increases rather than decreasing until it reaches its peak value and then starts decreasing. Under compressive strain, the thermal conductivity of monolayer boron nitride ribbons monolithically reduces rather than increasing. We use phonon spectrum and dispersion curves to investigate the mechanism responsible for the unexpected behavior. Our molecular dynamics modeling and density functional theory results show that application of longitudinal tensile strain leads to the reduction of the group velocities of longitudinal and transverse acoustic modes. Such a phonon softening mechanism acts to reduce the thermal conductivity of the nanoribbons. On the other hand, a significant increase in the group velocity (stiffening) of the flexural acoustic modes is observed, which counteracts the phonon softening effects of the longitudinal and transverse modes. The total thermal conductivity of the ribbons is a result of competition between these two mechanisms. At low tensile strain, the stiffening mechanism overcomes the softening mechanism which leads to an increase in the thermal conductivity. At higher tensile strain, the softening mechanism supersedes the stiffening and the thermal conductivity slightly reduces. Our simulations show that the decrease in the thermal conductivity under compressive strain is attributed to the formation of buckling defects which reduces the phonon mean free path. read less USED (low confidence) X.-K. Chen, Z.-X. Xie, W.-X. Zhou, L.-M. Tang, and K. Chen, “Thermal rectification and negative differential thermal resistance behaviors in graphene/hexagonal boron nitride heterojunction,” Carbon. 2016. link Times cited: 95 USED (low confidence) X.-K. Chen, Z.-X. Xie, W.-X. Zhou, and K. Chen, “The thermal conductivity in hybridised graphene and boron nitride nanoribbons modulated with strain,” Journal of Physics D: Applied Physics. 2016. link Times cited: 23 Abstract: Thermal transport properties in hybridised graphene and boro… read moreAbstract: Thermal transport properties in hybridised graphene and boron nitride ribbons (HGBNRs) under different strains are studied by using reverse nonequilibrium molecular dynamics simulations. It is found that the effect of strains on the thermal conductivity is different for different types of strains. When the tensile and shear strains are applied, the thermal conductivity can be modulated at least up to 50% at room temperature as the strain ε ranges from 0 to 0.2. However, when the compressive and flexural strains are respectively applied, the thermal conductivity is insensitive to the variation of the strain. In addition, it is also found that the thermal conductivity of HGBNRs depends sensitively on the dimension of the hybridised ribbon and the relative amount of h-BN to graphene. A brief analysis of these results is given. read less USED (low confidence) A. Chandra, P. Patra, and B. Bhattacharya, “Thermomechanical buckling of boron nitride nanotubes using molecular dynamics,” Materials Research Express. 2016. link Times cited: 19 Abstract: We study the thermal buckling behavior of precompressed boro… read moreAbstract: We study the thermal buckling behavior of precompressed boron-nitride nanotubes (BNNTs) using molecular dynamics simulations with Tersoff interatomic potential. We compute the critical buckling strains at near-zero temperature, and subsequently precompress the nanotubes at a certain fraction of this value followed by temperature ramping. The critical buckling temperature, Tcr, is marked by a sudden decrease of the internal force. We observe that (i) at small to moderate lengths, Tcr is higher for chiral nanotubes than for either armchair or zigzag nanotubes, (ii) Tcr decreases with increasing diameter unlike in thermal disintegration where disintegration temperatures rise with increasing diameter, and (iii) armchair nanotubes have an optimal length for which Tcr is maximum. We qualitatively explain the reasons for each of the findings. Thermomechanical buckling occurs predominantly in two ways depending on the length of the nanotube—while the shorter nanotubes fail by radial instability (shell-like behavior), the longer ones invariably fail due to bending-buckling (rod-like behavior). read less USED (low confidence) A. Kandemir, H. Yapicioglu, A. Kinaci, T. Çagin, and C. Sevik, “Thermal transport properties of MoS2 and MoSe2 monolayers,” Nanotechnology. 2016. link Times cited: 95 Abstract: The isolation of single- to few-layer transition metal dicha… read moreAbstract: The isolation of single- to few-layer transition metal dichalcogenides opens new directions in the application of two-dimensional materials to nanoelectronics. The characterization of thermal transport in these new low-dimensional materials is needed for their efficient implementation, either for general overheating issues or specific applications in thermoelectric devices. In this study, the lattice thermal conductivities of single-layer MoS2 and MoSe2 are evaluated using classical molecular dynamics methods. The interactions between atoms are defined by Stillinger–Weber-type empirical potentials that are developed to represent the structural, mechanical, and vibrational properties of the given materials. In the parameterization of the potentials, a stochastic optimization algorithm, namely particle swarm optimization, is utilized. The final parameter sets produce quite consistent results with density functional theory in terms of lattice parameters, bond distances, elastic constants, and vibrational properties of both single-layer MoS2 and MoSe2. The predicted thermal properties of both materials are in very good agreement with earlier first-principles calculations. The discrepancies between the calculations and experimental measurements are most probably caused by the pristine nature of the structures in our simulations. read less USED (low confidence) R. Martínez-Gordillo and M. Pruneda, “Polar discontinuities and 1D interfaces in monolayered materials,” Progress in Surface Science. 2015. link Times cited: 17 USED (low confidence) J. Peng, Y. Zhou, and K. Chen, “Influence of boundary types on rectifying behaviors in hexagonal boron-nitride/graphene nanoribbon heterojunctions,” Organic Electronics. 2015. link Times cited: 38 USED (low confidence) V. Tran, J. Saint-Martin, and P. Dollfus, “High thermoelectric performance in graphene nanoribbons by graphene/BN interface engineering,” Nanotechnology. 2015. link Times cited: 36 Abstract: The thermoelectric properties of in-plane heterostructures m… read moreAbstract: The thermoelectric properties of in-plane heterostructures made of Graphene and hexagonal boron nitride (BN) have been investigated by means of atomistic simulation. The heterostructures consist in armchair graphene nanoribbons to the sides of which BN flakes are periodically attached. This arrangement generates a strong mismatch of phonon modes between the different sections of the ribbons, which leads to a very small phonon conductance, while the electron transmission is weakly affected. In combination with the large Seebeck coefficient resulting from the BN-induced bandgap opening or broadening, it is shown that large thermoelectric figure of merit ZT > 0.8 can be reached in perfect structures at relatively low Fermi energy, depending on the graphene nanoribbon width. The high value ZT = 1.48 may even be achieved by introducing appropriately vacancies in the channel, as a consequence of further degradation of the phonon conductance. read less USED (low confidence) A. Tabarraei, “Thermal conductivity of monolayer hexagonal boron nitride nanoribbons,” Computational Materials Science. 2015. link Times cited: 71 USED (low confidence) A. Tabarraei and X. Wang, “A molecular dynamics study of nanofracture in monolayer boron nitride,” Materials Science and Engineering A-structural Materials Properties Microstructure and Processing. 2015. link Times cited: 35 USED (low confidence) Y. C. Chen, S. Lee, T.-H. Liu, and C.-C. Chang, “Thermal conductivity of boron nitride nanoribbons: Anisotropic effects and boundary scattering,” International Journal of Thermal Sciences. 2015. link Times cited: 30 USED (low confidence) S. Sarikurt, C. Sevik, A. Kinaci, J. Haskins, and T. Çagin, “Tailoring Thermal Conductivity of Ge/Si Core‐Shell Nanowires.” 2015. link Times cited: 1 USED (low confidence) S. Tan, L.-M. Tang, and K. Chen, “Phonon scattering and thermal conductance properties in two coupled graphene nanoribbons modulated with bridge atoms,” Physics Letters A. 2014. link Times cited: 7 USED (low confidence) M. Ren, J. Liu, L. Wang, and Q. Zheng, “Anomalous elastic buckling of hexagonal layered crystalline materials in the absence of structure slenderness,” arXiv: Materials Science. 2014. link Times cited: 23 USED (low confidence) J. Song and N. Medhekar, “Thermal transport in lattice-constrained 2D hybrid graphene heterostructures,” Journal of Physics: Condensed Matter. 2013. link Times cited: 20 Abstract: The thermal transport properties of hybrid graphene/h-BN het… read moreAbstract: The thermal transport properties of hybrid graphene/h-BN heterostructures are investigated using atomistic simulations. While the thermal conductivity is observed to be significantly limited perpendicular to the graphene/h-BN interface, it is tunable via a composition parallel to the interface. In particular we show that the thermal transport parallel to the interface can be understood by viewing the hybrid system as a series of individual embedded graphene nanoribbons (GNRs) constrained by neighboring h-BN. A mechanistic model is proposed to relate the thermal conductivities of the embedded and free-standing GNRs through a linear function of the composition. The model predictions are demonstrated to be in good agreement with the simulation results. read less USED (low confidence) I. M. Felix and L. Pereira, “Thermal conductivity of Thue–Morse and double-period quasiperiodic graphene-hBN superlattices,” International Journal of Heat and Mass Transfer. 2022. link Times cited: 5 USED (low confidence) A. Salmankhani et al., “A theoretical scenario for the mechanical failure of boron carbide nanotubes,” Computational Materials Science. 2021. link Times cited: 17 USED (low confidence) B. Zhao, X. Yu, Y. Liu, L. Yang, Z. Zhang, and B. Zhang, “Frictional characteristics of heterostructure film composed of graphene and H-BN with the consideration of defects,” Tribology International. 2021. link Times cited: 9 USED (low confidence) Y. Liu et al., “Mechanical properties and thickness-determined fracture mode of hexagonal boron nitride nanosheets under nanoindentation simulations,” Computational Materials Science. 2021. link Times cited: 12 USED (low confidence) O. Folorunso, Y. Hamam, R. Sadiku, S. Ray, and G. J. Adekoya, “Comparative study of graphene-polypyrrole and borophene-polypyrrole composites: molecular dynamics modeling approach,” Engineering Solid Mechanics. 2021. link Times cited: 2 Abstract: In the search for the solution to energy storage problems, t… read moreAbstract: In the search for the solution to energy storage problems, this study investigates the interfacial energy interaction and temperature stability of the composites made of polypyrrole-graphene-borophene (PPy-Gr-Bon) by using molecular dynamics simulations. From the calculated thermodynamics and interfacial energies of the system, comparisons between the ternary and the binary-binary systems were made. The materials in the entity show a good degree of temperature stability to a dynamic process at 300, 350, 400, and 450 K. Moreso, at 300 K, the interaction energy of PPy-Gr, PPy-Bon, and PPy-Gr-Bon are: -5.621e3 kcal/mol, -26.094e3 kcal/mol, and -28.206e3 kcal/mol respectively. The temperature stability of the systems is in the order of: PPy-Gr-Bon > PPy-Bon > PPy-Gr. The effect of temperature on the interaction energy of the systems was also investigated. The ternary system showed higher stability as the temperature increased. In addition, the radial distribution function computed for the three systems revealed that there is a strong, but non-chemical bonding interaction between PPy-Gr-Bon, Bon-PPy, and Gr-PPy. By considering the excellent mechanical properties of PPy-Gr-Bon and the already established high electrical conductivity and chemical stability of Gr, Bon and PPy, their composite is therefore suggested to be considered for the manufacturing of electrochemical electrodes. read less USED (low confidence) S. Sadeghzadeh, M. Ghojavand, and J. Mahmoudi, “Influence of Stone-Wales defects on the mechanical properties of graphene-like polyaniline (PANI) C3N nanosheets,” Diamond and Related Materials. 2020. link Times cited: 14 USED (low confidence) M. Dewapriya, R. Rajapakse, and S. Meguid, “Mechanical properties of two-dimensional materials: atomistic modeling and future directions.” 2020. link Times cited: 2 USED (low confidence) V. Vijayaraghavan and L. Zhang, “Computational Modelling of Hybrid Boron Nitride-Carbon Nanosheets,” Materials Today: Proceedings. 2019. link Times cited: 0 USED (low confidence) A. Wei, Y. Li, D. Datta, H. Guo, and Z. Lv, “Mechanical properties of graphene grain boundary and hexagonal boron nitride lateral heterostructure with controlled domain size,” Computational Materials Science. 2017. link Times cited: 20 USED (low confidence) S. Sarikurt, C. Sevik, A. Kinaci, J. Haskins, and T. Çagin, “Influence of Core-Shell Architecture Parameters on Thermal Conductivity of Si-Ge Nanowires,” MRS Proceedings. 2015. link Times cited: 0 Abstract: In this work, we investigate the influence of the core-shell… read moreAbstract: In this work, we investigate the influence of the core-shell architecture on nanowire (1D) thermal conductivity targeting to evaluate its validity as a strategy to achieve a better thermoelectric performance. To obtain the thermal conductivity values, equilibrium molecular dynamic simulations is applied to Si and Ge systems that are chosen to form core-shell nanostructures. To explore the parameter space, we have calculated thermal conductivity values of the Si-core/Ge-shell and Ge-core/Si-shell nanowires at different temperatures for different cross-sectional sizes and different core contents. Our results indicate that (1) increasing the cross-sectional area of pristine Si and pristine Ge nanowire increases the thermal conductivity (2) increasing the Ge core size in the Si-core/Ge-shell structure results in a decrease in the thermal conductivity values at 300 K (3) thermal conductivity of the Si-core/Ge-shell nanowires demonstrates a minima at specific core size (4) no significant variation in the thermal conductivity observed in nanowires for temperature values larger than 300 K (5) the predicted thermal conductivity around 10 W m −1 K −1 for the Si and Ge core-shell architecture is still high to get desired ZT values for thermoelectric applications. On the other hand, significant decrease in thermal conductivity with respect to bulk thermal conductivity of materials and pristine nanowires proves that employing core–shell architectures for other possible thermoelectric material candidates would serve valuable opportunities to achieve a better thermoelectric performance. read less USED (low confidence) S. Thomas and K. Ajith, “Molecular Dynamics Simulation of the Thermo-mechanical Properties of Monolayer Graphene Sheet☆,” Procedia Materials Science. 2014. link Times cited: 21 NOT USED (low confidence) S. Sinha, D. Kumar, S. Goel, and A. Patnaik, “Evaluating the elastic behaviour of boron nitride nanotube (BNNT) reinforced phenolic nanocomposites,” Engineering Research Express. 2023. link Times cited: 0 Abstract: The present analysis concerns investigation of the elastic b… read moreAbstract: The present analysis concerns investigation of the elastic behavior of boron nitride nanotube (BNNT)-reinforced phenolic nanocomposite using molecular dynamics (MD) simulations. In the investigation, an armchair BNNT with chiral vectors (10, 10) was used as reinforcement and novolac-type phenolic chains and formaldehyde mixture was used as a matrix. The crosslinking of phenolic chains and formaldehyde mixture was achieved to obtain the three-dimensional crosslinked structure reinforced with BNNT. In addition to the tensile elastic modulus, the glass transition temperature was evaluated for the bulk phenolic resin and the nanocomposite using the density-temperature relationship. Based on the results, it was concluded that 6.8% (volume fraction) of BNNT can enhance the elastic modulus of the composite by ∼15 times. Poisson’s ratio was found to be independent of the mixing ratio. It was also observed that reinforcement with BNNT can enhance the glass transition temperature of the nanocomposite. Continuum-based rule of mixture showed a good correlation with the MD predictions. read less NOT USED (low confidence) X. Wu et al., “Suppressed thermal transport in mathematically inspired 2D heterosystems,” Carbon. 2023. link Times cited: 1 NOT USED (low confidence) X. Jiang, H. Sun, K. Choudhary, H. Zhuang, and Q. Nian, “Interpretable Ensemble Learning for Materials Property Prediction with Classical Interatomic Potentials: Carbon as an Example,” ArXiv. 2023. link Times cited: 0 Abstract: Machine learning (ML) is widely used to explore crystal mate… read moreAbstract: Machine learning (ML) is widely used to explore crystal materials and predict their properties. However, the training is time-consuming for deep-learning models, and the regression process is a black box that is hard to interpret. Also, the preprocess to transfer a crystal structure into the input of ML, called descriptor, needs to be designed carefully. To efficiently predict important properties of materials, we propose an approach based on ensemble learning consisting of regression trees to predict formation energy and elastic constants based on small-size datasets of carbon allotropes as an example. Without using any descriptor, the inputs are the properties calculated by molecular dynamics with 9 different classical interatomic potentials. Overall, the results from ensemble learning are more accurate than those from classical interatomic potentials, and ensemble learning can capture the relatively accurate properties from the 9 classical potentials as criteria for predicting the final properties. read less NOT USED (low confidence) H. Nguyen, “Structural evolution of in-plane hybrid graphene/hexagonal boron nitride heterostructure upon heating.,” Journal of molecular graphics & modelling. 2023. link Times cited: 0 NOT USED (low confidence) L. Fan, X. Cai, H. Wang, J. Ye, Y. Hong, and Y. Feng, “Toughening two-dimensional hybrid materials by integrating carbon nanotubes,” Surfaces and Interfaces. 2022. link Times cited: 1 NOT USED (low confidence) H. Sun et al., “Graphene and 2D Hexagonal Boron Nitride Heterostructure for Thermal Management in Actively Tunable Manner,” Nanomaterials. 2022. link Times cited: 3 Abstract: Thermal management is a critical task for highly integrated … read moreAbstract: Thermal management is a critical task for highly integrated or high-power semiconductor devices. Low dimensional materials including graphene and single-layer hexagonal boron nitride (BN) are attractive candidates for this task because of their high thermal conductivity, semi-conductivity and other excellent physical properties. The similarities in crystal structure and chemistry between graphene and boron nitride provide the possibility of constructing graphene/BN heterostructures bearing unique functions. In this paper, we investigated the interfacial thermal transport properties of graphene/BN nanosheets via non-equilibrium molecular dynamics (NEMD) simulations. We observed a significant thermal rectification behavior of these graphene/BN nanosheets, and the rectification ratio increased with the system length increases up to 117%. This phenomenon is attributed to the mismatch of out-of-plane phonon vibration modes in two directions at the interface. In addition, we explored the underlying mechanism of the length dependence of the thermal transport properties. The results show promise for the thermal management of this two-dimensional heterostructure in an actively tunable manner. read less NOT USED (low confidence) Z. C. Huang, Z. Z. He, Y. Zhu, and H. Wu, “A general theory for the bending of multilayer van der Waals materials,” Journal of the Mechanics and Physics of Solids. 2022. link Times cited: 6 NOT USED (low confidence) N. Li et al., “Phonon transition across an isotopic interface,” Nature Communications. 2022. link Times cited: 0 NOT USED (low confidence) B. Mortazavi, F. Shojaei, M. Yagmurcukardes, A. Shapeev, and X. Zhuang, “Anisotropic and outstanding mechanical, thermal conduction, optical, and piezoelectric responses in a novel semiconducting BCN monolayer confirmed by first-principles and machine learning,” Carbon. 2022. link Times cited: 10 NOT USED (low confidence) B. Yao, Z. R. Liu, and R. F. Zhang, “EAPOTc: An integrated empirical interatomic potential optimization platform for compound solids,” Computational Materials Science. 2022. link Times cited: 1 NOT USED (low confidence) X. Wan et al., “Iron atom–cluster interactions increase activity and improve durability in Fe–N–C fuel cells,” Nature Communications. 2022. link Times cited: 91 NOT USED (low confidence) J. Luo et al., “Engineering dual oxygen simultaneously modified boron nitride for boosting adsorptive desulfurization of fuel,” Engineering. 2022. link Times cited: 9 NOT USED (low confidence) M. Mehrabani, M. M. Khatibi, S. Sadeghzadeh, and M. Ashory, “Tailoring the effects of interface physics on the free vibration of graphene-boron nitride heterostructure,” Diamond and Related Materials. 2022. link Times cited: 0 NOT USED (low confidence) J. Cai, E. Estakhrianhaghighi, and A. Akbarzadeh, “Functionalized Graphene Origami Metamaterials with Tunable Thermal Conductivity,” MatSciRN EM Feeds. 2022. link Times cited: 11 Abstract: Graphene with tunable thermo-mechanical property is of great… read moreAbstract: Graphene with tunable thermo-mechanical property is of great importance for next-generation thermal management devices. Distinct from previously reported porous graphene materials that tune the thermal conductivity at the cost of degrading their mechanical properties, non-porous hydrogenated graphene origami metamaterial exhibits a unique combination of tunable thermal conductivity, high strength, and enhanced stretchability. Through molecular dynamics simulation, an extremely broad range of thermal conductivity can be obtained by tuning the geometrical parameters of the Miura-ori nanoarchitecture of graphene origami, altering the adatom types and density, designing new origami patterns, and applying mechanical strains. By analyzing and comparing the results from atomistic and continuum-based simulations, the effect of length scale on the thermal property of graphene origami metamaterials is explored. The temperature distribution and the phonon density of states of the proposed graphene origami are examined to illustrate the heat conduction mechanism. Finally, 3D graphene origami metamaterials are constructed based on the coupling and assembling of graphene origami strips, and their thermo-mechanical performance is elucidated. Negative coefficients of thermal expansion are obtained in graphene origami nanotubes. The introduced strategy for controlling the thermo-mechanical properties of graphene metamaterials can open up new avenues for developing thermoelectric devices, heat management systems, and flexible nanoelectronics. read less NOT USED (low confidence) S. Wyant, A. Rohskopf, and A. Henry, “Machine learned interatomic potentials for modeling interfacial heat transport in Ge/GaAs,” Computational Materials Science. 2021. link Times cited: 4 NOT USED (low confidence) K. Dheeraj and S. P. Sathian, “The disparate effect of strain on thermal conductivity of 2-D materials.,” Physical chemistry chemical physics : PCCP. 2021. link Times cited: 1 Abstract: Thermal transport in 2-D (dimensional) structures is highly … read moreAbstract: Thermal transport in 2-D (dimensional) structures is highly susceptible to external perturbations such as strain, owing to their high surface-to-volume ratio. In this study, we investigate the influence of strain on the thermal conductivity of flat (graphene and hexagonal boron nitride), buckled and puckered (molybdenum disulfide and black phosphorous) 2-D materials. Unlike bulk materials where the thermal conductivity reduces with strain, the thermal conductivity of 2-D materials under strain is observed to be unique and dependent on the material considered. To understand such diverse strain-dependent thermal conductivity in 2-D materials, the phonon mode properties are calculated. It was observed that the strain softens the longitudinal mode (LA), whereas the out-of-plane acoustic mode (ZA) undergoes stiffening albeit various extents. In flat 2-D materials, the dispersion of ZA mode is linearized under strain while it tends to linearize in buckled and puckered structures. The variation in the phonon group velocity of ZA mode coupled with the anomalous behavior of the phonon lifetime of acoustic modes results in a diverse strain dependence of the thermal conductivity of 2-D materials. Our findings offer insight into the influence of strain of 2-D materials and will be helpful in tailoring the thermal properties of these materials for various applications such as nanoelectronics and thermoelectric devices. read less NOT USED (low confidence) A. Mayelifartash, M. A. Abdol, and S. Sadeghzadeh, “Thermal conductivity and interfacial thermal resistance behavior for the polyaniline-boron carbide heterostructure.,” Physical chemistry chemical physics : PCCP. 2021. link Times cited: 9 Abstract: In this paper, by employing non-equilibrium molecular dynami… read moreAbstract: In this paper, by employing non-equilibrium molecular dynamics simulations (NEMD), the thermal conductance of the hybrid formed by polyaniline (C3N) and boron carbide (BC3) in both the armchair and zigzag configurations has been investigated. For this purpose, by creating superlattices with different periodic lengths (lp), the thermal conductivity of the entire hybrid at various lengths and also at infinity has been reported. In addition, the thermal conductivity of each sheet and also the interface thermal resistance (ITR) between them under various conditions have been computed and how this changes upon varying the length, width, temperature, uniaxial strain, point vacancy, and circular defects has been recorded and plotted. Based on our findings, the increasing length of the hybrid results in a higher thermal conductance owing to the higher thermal conductivity of each sheet and the lower amount of ITR. However, altering the width does not have a noticeable effect on the thermal transport if the periodic boundary conditions are applied. Moreover, the results revealed that the rising temperature and uniaxial strain reduced the thermal conductivity of each sheet, whereas the ITR increased by increasing the temperature. Also, studying the effect of the presence of defects on the thermal transport demonstrated that increasing the size of the defects or the density leads to considerably lower thermal conductivity of each sheet and also a higher ITR. Our results also revealed the thermal conductivity of hybrid C3N-BC3 can reach 506 W m-1 K-1, which is higher in comparison to other two-dimensional hybrid materials. This result provides valuable information on the thermal transport and phonon behavior for use in nanoelectronic and thermoelectric devices. read less NOT USED (low confidence) P. Ying, J. Zhang, Y. Du, and Z. Zhong, “Effects of coating layers on the thermal transport in carbon nanotubes-based van der Waals heterostructures,” Carbon. 2021. link Times cited: 10 NOT USED (low confidence) Y. Ren, Y. Wu, B. Xiao, K. Wu, and D. Cubero, “Heat transport and surface functionalization in nanocomposites of boron nitride nanotubes and polyethylene.,” Physical chemistry chemical physics : PCCP. 2021. link Times cited: 2 Abstract: This work explores the possibility for improving heat transp… read moreAbstract: This work explores the possibility for improving heat transport in a polymeric, electrical insulating material, such as polyethylene, by adding boron nitride nanotubes - a heat superdiffusive material. We use molecular dynamics simulations to study the nanocomposites formed by addition of the nanotubes to both amorphous and crystalline polyethylene, and also investigate the effect of surface functionalization using a silane coupling agent, which, being covalently attached to both the nanofiller and the polymer matrix, facilitates the heat transport between them. Even though transport is shown to deteriorate in each simulation when the coupling agents are added, they are expected to favor the nucleation of the crystalline regions about the nanotubes, thus significantly boosting heat conduction in the material along their direction. read less NOT USED (low confidence) Z. Xiong, T. Zhang, and X. Li, “Analytical Models for Predicting the Nonlinear Stress–Strain Relationships and Behaviors of Two-Dimensional Carbon Materials,” Journal of Applied Mechanics. 2021. link Times cited: 1 Abstract:
Due to having a single atom layer, two-dimensional (2D) ma… read moreAbstract:
Due to having a single atom layer, two-dimensional (2D) materials represented by graphene monolayers exhibit unique and excellent mechanical properties, such as ultrahigh moduli and strengths. A large number of experiments and atomistic simulations have demonstrated nonlinear stress–strain responses. However, there is no theoretical model that analytically describes the relationships between nonlinear mechanical properties and interatomic interaction parameters of 2D materials. Here, we developed a nonlinear stick-spiral model for four typical 2D materials (including graphene, γ-graphyne, β-graphyne, and hexagonal boron nitride) based on a molecular mechanics model. By using the perturbation method, we derived a series of analytical expressions for nonlinear stress–strain relationships and elastic constants of these 2D materials under uniaxial tension along the zigzag and armchair directions. Our analytic models indicated that both Young’s moduli and Poisson’s ratios of these 2D materials are isotropic and dominate the linear elastic deformation, while their third-order moduli are orientation-dependent and essentially characterize the nonlinear stress–strain responses. The nonlinear stress–strain relationships, elastic constants, and atomic behaviors (such as bond elongation and bond angle variation during deformation) predicted from our analytical models are in good agreement with those from atomistic simulations and previous experiments. Our analytical models further demonstrated that the mechanical properties and behaviors of 2D materials are linked with their bonding and atomic structures (from a quantitative perspective) and are mainly determined by stiffnesses for bond stretching, angle variation, and bond lengths. Our current study provides an effective and accurate analytical approach for investigating the nonlinear behaviors of 2D materials. read less NOT USED (low confidence) Y. Zhang, J. Ma, N. Wei, J. Yang, and Q. Pei, “Recent progress in the development of thermal interface materials: a review.,” Physical chemistry chemical physics : PCCP. 2021. link Times cited: 30 Abstract: Modern electronic devices are characterized by high-power an… read moreAbstract: Modern electronic devices are characterized by high-power and high-frequency with excessive heat accumulation. Thermal interface materials (TIMs) are of crucial importance for efficient heat dissipation to maintain proper functions and lifetime for these devices. The most promising TIMs are those polymer-based nanocomposites consisting of polymers and low-dimensional materials with high thermal conductivity (TC). This perspective summarizes the recent progress on the thermal transport properties of newly discovered one-dimensional (1D) nanomaterials and two-dimensional (2D) nanomaterials as well as three-dimensional (3D) nanostructures consisting of these 1D and 2D nanomaterials. Moreover, the applications of various nanomaterials in polymer nanocomposites for advanced TIMs are critically reviewed and the mechanism of TC enhancement is analysed. It is hoped that the present review could provide better understanding of the thermal transport properties of recently developed 2D nanomaterials and various 3D nanostructures as well as relevant polymer-based TIMs, shedding more light on the thermal management research. read less NOT USED (low confidence) W. Yao, L. Fan, and Z. Zhang, “Research on correlation of mechanical behavior of multilayer in-plane graphene/hexagonal boron nitride heterostructures in the presence of Stone-Wales defects and interlayer sp3 bonds with multiple physical fields,” Computational Materials Science. 2020. link Times cited: 4 NOT USED (low confidence) J. Song et al., “Thermal transport properties of graphite carbon nitride.,” Physical chemistry chemical physics : PCCP. 2020. link Times cited: 2 Abstract: Graphite carbon nitride (GCN), which can be regarded as a ni… read moreAbstract: Graphite carbon nitride (GCN), which can be regarded as a nitrogen heteroatom-substituted graphite framework, has attracted great attention as a new 2D layered structure material with semiconductor electronic characteristics. Using molecular dynamics simulations, the in-plane thermal conductivity and cross-plane thermal resistance of two GCN structures (i.e., triazine-based and heptazine-based) are investigated. Our results show that the in-plane thermal conductivities of the triazine-based and heptazine-based GCN monolayers along the armchair direction are 55.39 and 17.81 W m-1 K-1, respectively. The cross-plane thermal resistance decreases with increasing layer number and reaches asymptotic values of 3.6 × 10-10 and 9.3 × 10-10 m2 K W-1 at 40 layers for triazine-based and heptazine-based GCN, respectively. The in-plane thermal conductivity can be effectively manipulated by changing the temperature and applying strain, while it is insensitive to the number of layers, which is in sharp contrast to that of graphene. Moreover, the cross-plane thermal resistance decreases monotonically with temperature and coupling strength, and can be modulated by external strain. Surprisingly, the cross-plane tensile strain can reduce the thermal resistance of the heptazine-based GCN. Our study serves as a guide to groups interested in the physical properties of GCN. read less NOT USED (low confidence) S. Thomas and M. A. Zaeem, “A new planar BCN lateral heterostructure with outstanding strength and defect-mediated superior semiconducting to metallic properties.,” Physical chemistry chemical physics : PCCP. 2020. link Times cited: 20 Abstract: Motivated by the recent synthesis of boron-carbon-nitride (B… read moreAbstract: Motivated by the recent synthesis of boron-carbon-nitride (BCN) monolayers with different atomic compositions, we propose a novel planar BCN lateral heterostructure with a combination of graphene and hexagonal boron nitride (h-BN) counterparts. Density functional theory (DFT) and classical molecular dynamics (CMD) simulations are integrated to examine the effects of defects (vacancy and Stone-Wales (SW) defects) and temperature on the physical properties of the BCN heterostructure. We found that structures with SW defects possess the lowest (4.10 eV) and those with vacancy defects possess the highest (7.32 eV) defect formation energy. DFT results show that the computed mechanical properties of the pristine and defective BCN are complementary to those of graphene, and CMD results establish that the size effect on mechanical properties is insignificant. DFT calculations also reveal that the pristine and SW defect filled BCN retain the direct semiconducting electronic characteristics, while C and B mono-vacancies interestingly make it a metallic material due to the slight overlapping of the bands at the Fermi level, and the N mono-vacancy causes a small indirect bandgap (0.08 eV). Besides, the presence of defects significantly changes the work function of BCN due to the lattice rearrangement. Herein, we argue that the defect mediated design of BCN heterostructures can provide new opportunities for plausible applications including energy conversion and storage, and high speed optical and electronic devices due to their semiconducting-metallic functionality and superior mechanical properties. read less NOT USED (low confidence) R. Tromer et al., “Electronic, optical and thermoelectric properties of boron-doped nitrogenated holey graphene.,” Physical chemistry chemical physics : PCCP. 2020. link Times cited: 8 Abstract: We employ first principles calculations to investigate the e… read moreAbstract: We employ first principles calculations to investigate the electronic, optical, and thermoelectric properties of ten boron-doped nitrogenated holey graphene (NHG) monolayers. We find that most of the proposed structures remain stable during ab initio molecular dynamics simulations, in spite of their increased formation energies. Density functional theory calculations employing a hybrid functional predict band gaps ranging from 0.73 eV to 2.30 eV. In general, we find that boron doping shifts optical absorption towards the visible spectrum, and also reduces light reflection in this region. On the other hand, the magnitude of optical absorption coefficients are reduced. Regarding the thermoelectric properties, we predict that boron doping can enhance the figure of merit ZT of NHG by up to 55%. Our results indicate that boron-doped NHG monolayers may find application in solar cells and thermoelectric devices. read less NOT USED (low confidence) O. Olaniyan, L. Moskaleva, R. Mahadi, E. Igumbor, and A. Bello, “Tuning the electronic structure and thermodynamic properties of hybrid graphene-hexagonal boron nitride monolayer,” FlatChem. 2020. link Times cited: 4 NOT USED (low confidence) H. Qin, Y. Yan, H. Liu, J. Liu, Y.-W. Zhang, and Y. Liu, “Modified Timoshenko beam model for bending behaviors of layered materials and structures,” Extreme Mechanics Letters. 2020. link Times cited: 10 NOT USED (low confidence) H. Cheng et al., “Covalent coupling regulated thermal conductivity of poly(vinyl alcohol)/boron nitride composite film based on silane molecular structure,” Composites Part A-applied Science and Manufacturing. 2020. link Times cited: 29 NOT USED (low confidence) M. An et al., “Mass difference and polarization lead to low thermal conductivity of graphene-like carbon nitride (C3N),” Carbon. 2020. link Times cited: 30 NOT USED (low confidence) J. Song et al., “Effect of strain and defects on the thermal conductance of the graphene/hexagonal boron nitride interface.,” Physical chemistry chemical physics : PCCP. 2020. link Times cited: 12 Abstract: In-plane heterojunctions, obtained by seamlessly joining two… read moreAbstract: In-plane heterojunctions, obtained by seamlessly joining two or more nanoribbon edges of isolated two-dimensional atomic crystals such as graphene and hexagonal boron nitride, are emerging as nanomaterials for the development of future multifunctional devices. The thermal transport behavior at the interface of these heterojunctions plays a pivotal role in determining their functional performance. Using molecular dynamics simulations, the interfacial thermal conductance of graphene/hexagonal boron nitride (GE/BN) in-plane heterojunctions was investigated. The GE/BN heterostructure has a remarkably high interfacial thermal conductance, and thermal rectification occurs at the interface. The results also show that the interfacial thermal conductance is effectively modulated by strain and defect engineering. The atomic defect location can affect the phonon transmission at the interface. Interestingly, compared with the nitrogen doping effect, the boron doping defect can more effectively facilitate vibrational coupling at the interface in the graphene sheet. Stress distribution and vibrational spectral analyses are performed to elucidate the thermal transport mechanism. The results of this study may provide a foundation for future research attempting to manipulate the interfacial thermal conductance in other two-dimensional heterostructures. read less NOT USED (low confidence) B. Mortazavi et al., “Efficient machine-learning based interatomic potentialsfor exploring thermal conductivity in two-dimensional materials,” Journal of Physics: Materials. 2020. link Times cited: 39 Abstract: It is well-known that the calculation of thermal conductivit… read moreAbstract: It is well-known that the calculation of thermal conductivity using classical molecular dynamics (MD) simulations strongly depends on the choice of the appropriate interatomic potentials. As proven for the case of graphene, while most of the available interatomic potentials estimate the structural and elastic constants with high accuracy, when employed to predict the lattice thermal conductivity they however lead to a variation of predictions by one order of magnitude. Here we present our results on using machine-learning interatomic potentials (MLIPs) passively fitted to computationally inexpensive ab-initio molecular dynamics trajectories without any tuning or optimizing of hyperparameters. These first-attempt potentials could reproduce the phononic properties of different two-dimensional (2D) materials obtained using density functional theory (DFT) simulations. To illustrate the efficiency of the trained MLIPs, we consider polyaniline C3N nanosheets. C3N monolayer was selected because the classical MD and different first-principles results contradict each other, resulting in a scientific dilemma. It is shown that the predicted thermal conductivity of 418 ± 20 W mK−1 for C3N monolayer by the non-equilibrium MD simulations on the basis of a first-attempt MLIP evidences an improved accuracy when compared with the commonly employed MD models. Moreover, MLIP-based prediction can be considered as a solution to the debated reports in the literature. This study highlights that passively fitted MLIPs can be effectively employed as versatile and efficient tools to obtain accurate estimations of thermal conductivities of complex materials using classical MD simulations. In response to remarkable growth of 2D materials family, the devised modeling methodology could play a fundamental role to predict the thermal conductivity. read less NOT USED (low confidence) V. Sharma, H. L. Kagdada, P. Jha, P. Śpiewak, and K. Kurzydłowski, “Thermal transport properties of boron nitride based materials: A review,” Renewable & Sustainable Energy Reviews. 2020. link Times cited: 72 NOT USED (low confidence) W. Yao and L. Fan, “Research on the correlation of mechanical properties of BN-graphene-BN/BN vertically-stacked nanostructures in the presence of interlayer sp3 bonds and nanopores with temperature.,” Physical chemistry chemical physics : PCCP. 2020. link Times cited: 19 Abstract: In this study, we investigate the coupling of an internal fi… read moreAbstract: In this study, we investigate the coupling of an internal field (defect field-sp3 bonds and nanopores) and an external field (strain and temperature). Simultaneously, we provide a design idea of hybrid materials. The mechanical properties of hybrid materials under the condition of internal and external field coupling were studied. When nanopores and sp3 bonds are considered simultaneously, we found that internal (sp3 bonds and defects) and external field (temperature and strain fields) have a negative chain reaction on the mechanical properties of BN-graphene-BN/BN vertically-stacked nanostructures, and the negative chain reaction will gradually increase with the change in parameters (such as the increase in temperature). The sp3 bonds can be regarded as a special defect, which will increase the initial strain of the system. In addition, the mechanical properties of the nanostructure, containing square nanopores in the boron nitride region are most sensitive to temperature change, relative to the nanopore in the other two regions. Atoms (around square nanopores) are more likely to overcome the binding energy and lose stability from the inherent equilibrium position, relative to that of circular nanopores. read less NOT USED (low confidence) R. Tromer, I. M. Felix, A. Freitas, S. Azevedo, and L. Pereira, “Diboron-porphyrin monolayer: A new 2D semiconductor,” Computational Materials Science. 2020. link Times cited: 16 NOT USED (low confidence) Y. Zhang and L. Wang, “Effects of the Van der Waals Force on the Vibration of Typical Multi-layered Two-dimensional Nanostructures,” Scientific Reports. 2020. link Times cited: 6 NOT USED (low confidence) Z. Zhou, D. Fan, and H. Liu, “Realizing high thermoelectric performance with comparable p- and n-type figure-of-merits in a graphene/h-BN superlattice monolayer.,” Physical chemistry chemical physics : PCCP. 2019. link Times cited: 5 Abstract: Carbon-based structures are a superior alternative for unlea… read moreAbstract: Carbon-based structures are a superior alternative for unleashing the thermoelectric potential of earth-abundant and environmentally friendly materials. Here we design a hybrid graphene/h-BN superlattice monolayer and investigate its thermoelectric properties based on density functional theory and accurate solution of Boltzmann transport equations. Compared with that of pristine graphene, the lattice thermal conductivity of the superlattice structure is more than two orders of magnitude lower ascribed to the significantly increased phonon scattering originating from the mixed-bond characteristics. Besides, the obvious valley anisotropy near the electronic band edge leads to an ultrahigh power factor along the zigzag direction, which in turn gives an n-type ZT value as high as 2.5 at 1100 K. Moreover, it is interesting to find that the thermoelectric performance of p-type system can be enhanced to be comparable with that of n-type one by appropriate substitution of the nitrogen atom with phosphorus, which can suppress the lattice thermal conductivity but nearly have no effect on the hole transport. read less NOT USED (low confidence) X.-K. Chen et al., “Highly efficient thermal rectification in carbon/boron nitride heteronanotubes,” Carbon. 2019. link Times cited: 39 NOT USED (low confidence) W. Feng et al., “A cross-interface model for thermal transport across the interface between overlapped nanoribbons.,” Physical chemistry chemical physics : PCCP. 2019. link Times cited: 14 Abstract: The application of low-dimensional materials for heat dissip… read moreAbstract: The application of low-dimensional materials for heat dissipation requires a comprehensive understanding of thermal transport at cross-interfaces, which widely exist in various composite materials and electronic devices. In this work, an analytical model is proposed, named as the cross-interface model (CIM), to accurately reveal the essential mechanism of the two-dimensional thermal transport at cross-interfaces. The applicability of CIM is validated through a comparison of the analytical results with molecular dynamics simulations for a typical cross-interface between two overlapped boron nitride nanoribbons. Besides, it is found that both the thermal resistances and the factor, η, has an important influence on the thermal transport. These investigations would deepen the understanding of the thermal transport at cross-interfaces and also facilitate the application of low-dimensional materials in thermal management. read less NOT USED (low confidence) V. Zalizniak and O. A. Zolotov, “Embedded-atom method interatomic potential for boron nanostructures,” Journal of Molecular Modeling. 2019. link Times cited: 2 NOT USED (low confidence) S. Li, Z. X. Guo, and J.-wen Ding, “Interface thermal transport of graphene-based intralayer heterostructures,” Physica B: Condensed Matter. 2019. link Times cited: 6 NOT USED (low confidence) B. Liu and K. Zhou, “Recent progress on graphene-analogous 2D nanomaterials: Properties, modeling and applications,” Progress in Materials Science. 2019. link Times cited: 208 NOT USED (low confidence) H. Yang, Z. Zhang, J. Zhang, and X. Zeng, “Machine learning and artificial neural network prediction of interfacial thermal resistance between graphene and hexagonal boron nitride.,” Nanoscale. 2018. link Times cited: 57 Abstract: High-performance thermal interface materials (TIMs) have att… read moreAbstract: High-performance thermal interface materials (TIMs) have attracted persistent attention for the design and development of miniaturized nanoelectronic devices; however, a large number of potential new materials exist to form these heterostructures and the explorations of their thermal properties are time consuming and expensive. In this work, we train several supervised machine learning (ML) and artificial neural network (ANN) models to predict the interfacial thermal resistance (R) between graphene and hexagonal boron-nitride (hBN) with only the knowledge of the system temperature, coupling strength between two layers, and in-plane tensile strains. The training data were obtained by high-throughput computations (HTCs) of R using classical molecular dynamics (MD) simulations. Four different ML models, i.e., linear regression, polynomial regression, decision tree and random forest, are explored. A pair of one dense layer ANNs and another pair of two dense layer deep neural networks (DNNs) are also investigated. It is reported that the DNN models provide better R prediction results compared to the ML models. The thermal property predictions using HTC and ML/ANN models are applicable to a wide range of materials and open up new perspectives in the explorations of TIMs. read less NOT USED (low confidence) X. Liu and M. Hersam, “Interface Characterization and Control of 2D Materials and Heterostructures,” Advanced Materials. 2018. link Times cited: 118 Abstract: 2D materials and heterostructures have attracted significant… read moreAbstract: 2D materials and heterostructures have attracted significant attention for a variety of nanoelectronic and optoelectronic applications. At the atomically thin limit, the material characteristics and functionalities are dominated by surface chemistry and interface coupling. Therefore, methods for comprehensively characterizing and precisely controlling surfaces and interfaces are required to realize the full technological potential of 2D materials. Here, the surface and interface properties that govern the performance of 2D materials are introduced. Then the experimental approaches that resolve surface and interface phenomena down to the atomic scale, as well as strategies that allow tuning and optimization of interfacial interactions in van der Waals heterostructures, are systematically reviewed. Finally, a future outlook that delineates the remaining challenges and opportunities for 2D material interface characterization and control is presented. read less NOT USED (low confidence) X.-K. Chen, J.-wen Hu, X. Wu, P. Jia, Z.-H. Peng, and K. Chen, “Tunable thermal rectification in graphene/hexagonal boron nitride hybrid structures,” Journal of Physics D: Applied Physics. 2018. link Times cited: 26 Abstract: Using non-equilibrium molecular dynamics simulations, we inv… read moreAbstract: Using non-equilibrium molecular dynamics simulations, we investigate thermal rectification (TR) in graphene/hexagonal boron nitride (h-BN) hybrid structures. Two different structural models, partially substituting graphene into h-BN (CBN) and partially substituting h-BN into graphene (BNC), are considered. It is found that CBN has a significant TR effect while that of BNC is very weak. The observed TR phenomenon can be attributed to the resonance effect between out-of-plane phonons of graphene and h-BN domains in the low-frequency region under negative temperature bias. In addition, the influences of ambient temperature, system size, defect number and substrate interaction are also studied to obtain the optimum conditions for TR. More importantly, the TR ratio could be effectively tuned through chemical and structural diversity. A moderate C/BN ratio and parallel arrangement are found to enhance the TR ratio. Detailed phonon spectra analyses are conducted to understand the thermal transport behavior. This work extends hybrid engineering to 2D materials for achieving TR. read less NOT USED (low confidence) Y. Gao and B. Xu, “Controllable Interface Junction, In-Plane Heterostructures Capable of Mechanically Mediating On-Demand Asymmetry of Thermal Transports.,” ACS applied materials & interfaces. 2017. link Times cited: 20 Abstract: Designing structures with thermal rectification performance … read moreAbstract: Designing structures with thermal rectification performance that can be regulated by or adapted to mechanical deformation is in great demand in wearable electronics. Herein, using nonequilibrium molecular dynamics simulation, we present an in-plane graphene-boron nitride heterostructure with a controlled interface junction and demonstrate that its thermal transport ability is asymmetric when reversing the direction of heat flow. Such thermal rectification performance can be further regulated by applying an external tensile loading due to the mitigation of stress concentration, phonon resonance, and phonon localization. The analyses on heat flow distribution, vibrational spectra, and phonon participation suggest that the out-of-plane phonon modes dominate thermal rectification at a small tensile strain, while the mechanical stress plays a dominant role in regulation at a large tensile strain due to the weakened localization of out-of-plane phonon modes. The effect of tensile loading on the thermal rectification is demonstrated by selective interface junction-enabled heterostructures, and the results indicate that both asymmetry and direction of thermal transport can be controlled by introducing defects to the interface junction and/or applying mechanical tensile strain. These findings and models are expected to provide an immediate guidance for designing and manufacturing 2D material-based devices with mechanically tunable thermal management capabilities. read less NOT USED (low confidence) N. Han, H. Liu, J. Zhang, J. Gao, and J. Zhao, “Atomistic understanding of the lateral growth of graphene from the edge of an h-BN domain: towards a sharp in-plane junction.,” Nanoscale. 2017. link Times cited: 16 Abstract: The in-plane combination of graphene (G) and hexagonal-boron… read moreAbstract: The in-plane combination of graphene (G) and hexagonal-boron nitride (h-BN) leads to lateral h-BN/G heterostructures, which are promising candidates for novel two-dimensional electronics. The quality of the interface between G and h-BN domains is crucial for the device performance. By comprehensive first-principles calculations, we explore the heteroepitaxial growth of graphene along the edge of an h-BN domain on a Cu(111) surface and compare it with that on a Cu(111) terrace. We find that the graphene nucleation site strongly depends on the chemical potential of carbon and predeposited h-BN coverage. Under the suitable carbon concentration and coverage of h-BN, graphene mainly grows along the h-BN edge, leading to a sharp and straight h-BN/G interface. Our results provide insightful knowledge to synthesize well-defined h-BN/G and other lateral heterostructures. read less NOT USED (low confidence) X.-K. Chen, J. Liu, Z.-H. Peng, D. Du, and K. Chen, “A wave-dominated heat transport mechanism for negative differential thermal resistance in graphene/hexagonal boron nitride heterostructures,” Applied Physics Letters. 2017. link Times cited: 60 Abstract: Nonlinear thermal transport in graphene/hexagonal boron nitr… read moreAbstract: Nonlinear thermal transport in graphene/hexagonal boron nitride (h-BN) heterostructure is investigated by the nonequilibrium molecular dynamics method. It is found that negative differential thermal resistance (NDTR) will appear as the applied temperature difference increases. Detailed phonon spectra analysis reveals that the excited out-of-plane acoustic wave plays an important role in the heat transport across such interface. That is, the mechanical wave results in a significant mismatch between the lattice vibrations of graphene and h-BN domains and hinders interfacial thermal transport. In addition, NDTR can be tuned through the temperature parameter. Interestingly, the regime of NDTR becomes smaller and eventually vanishes with increasing the heterostructure length. However, NDTR is insensitive to the variation of system width. The work may be useful for nanoscale thermal managements utilizing the graphene/h-BN heterostructure. read less NOT USED (low confidence) S. J. Mahdizadeh and G. Akhlamadi, “Optimized Tersoff empirical potential for germanene.,” Journal of molecular graphics & modelling. 2017. link Times cited: 21 NOT USED (low confidence) Y. Zhou, Z. X. Guo, H. Cao, S. Chen, H. Xiang, and X. Gong, “Thermal conductivity of disordered two-dimensional binary alloys.,” Nanoscale. 2016. link Times cited: 4 Abstract: Using non-equilibrium molecular dynamics simulations, we hav… read moreAbstract: Using non-equilibrium molecular dynamics simulations, we have studied the effect of disorder on the thermal conductivity of two-dimensional (2D) C1-xNx alloys. We find that the thermal conductivity not only depends on the substitution concentration of nitrogen, but also strongly depends on the disorder distribution. A general linear relationship is revealed between the thermal conductivity and the participation ratio of phonons in 2D alloys. Localization mode analysis further indicates that the thermal conductivity variation in the ordered alloys can be attributed to the number of inequivalent atoms. As for the disordered alloys, we find that the thermal conductivity variation can be described by a simple linear formula with the disorder degree and the substitution concentration. The present study suggests some general guidance for phonon manipulation and thermal engineering in low dimensional alloys. read less NOT USED (low confidence) J. Nakamura and A. Akaishi, “Anomalous enhancement of Seebeck coefficients of the graphene/hexagonal boron nitride composites,” Japanese Journal of Applied Physics. 2016. link Times cited: 5 Abstract: Thermoelectric devices convert heat energy to electric power… read moreAbstract: Thermoelectric devices convert heat energy to electric power. The dimensionless thermoelectric figure of merit, ZT, is used as a standard criterion for efficiency of thermoelectric conversion. This criterion requires a high Seebeck coefficient, a high electric conductivity, and a low thermal conductivity. In this regard, PbTe, BiTe, and their alloys consisting of relatively heavier elements have been found to show higher values of ZT. In this paper, we focus on the potential of graphene-based composites as thermoelectric materials. Graphene was considered to be a disadvantageous material because of its extremely high thermal conductance and relatively low Seebeck coefficient. However, it has been reported recently that a structural modulation is an effective way of raising the thermoelectric ability of graphene. We introduce the recent progress in the design of graphene-based materials for thermoelectric devices. In particular, we provide a focused investigation of our recent progress regarding the thermopower enhancement in nanoarchitectonics, superlattices, and composites consisting of graphene and hexagonal BN nanoribbons. It has been shown that low-dimensional modulations are effective ways of obtaining a high thermoelectric performance of graphene-based materials. read less NOT USED (low confidence) X. Liu, G. Zhang, and Y.-W. Zhang, “Topological Defects at the Graphene/h-BN interface Abnormally Enhance Its Thermal Conductance.,” Nano letters. 2016. link Times cited: 110 Abstract: Low thermal conductance across interface is often the limiti… read moreAbstract: Low thermal conductance across interface is often the limiting factor in managing heat in many advanced device applications. The most commonly used approach to enhance the thermal conductance is to reduce/eliminate the interfacial structural defects. Using a graphene/h-BN (Gr/h-BN) interface, we show surprisingly that topological defects are able to enhance the thermal conductance across the interface. It is found that the phonon transmission across the Gr/h-BN interface with 5|7 defects is higher than that of the pristine interface, which is in strong contrast to the common notion that interface defects promote phonon scattering. By analyzing the strain distribution and phonon vibrational spectra, we find that this abnormal enhancement in interfacial thermal conductance originates from the localization of the stress fields arising from misfit dislocations and their out-of-plane deformations at the interface. In the presence of the defects, the overall mismatch strain is reduced. In addition, the out-of-plane deformations screen the long-ranged dislocation strain fields, resulting in the stress fields to be localized only at the cores of the defects. This abnormal mechanism provides a new dimension to enhance the interfacial thermal conductance in two-dimensional heterostructures. read less NOT USED (low confidence) X. Chen, B. Wu, and Y. Liu, “Direct preparation of high quality graphene on dielectric substrates.,” Chemical Society reviews. 2016. link Times cited: 75 Abstract: Graphene, an amazing two-dimensional material with excellent… read moreAbstract: Graphene, an amazing two-dimensional material with excellent physical properties, has attracted great attention in various disciplines. Both fundamental studies and applications require graphene samples with controlled parameters including their quality, size, crystallinity, layer number and so on. While graphene can be prepared by direct exfoliation from mother materials or growth on transition metals, the uncontrolled production or the additional complex transfer process has been challenging for graphene applications. Direct preparation on a desired dielectric substrate is an important research direction that potentially addresses these problems. Many advances have been made in the past few years, and this tutorial review provides a brief summary of ways of preparing graphene on dielectric substrates. Various methods including the annealing method, direct chemical vapor deposition graphene synthesis on conventional dielectric substrates and hexagonal boron nitride layers are systematically reviewed and discussed. The main problems and further directions in this field are also presented. read less NOT USED (low confidence) R. Kumar and A. Parashar, “Atomistic modeling of BN nanofillers for mechanical and thermal properties: a review.,” Nanoscale. 2016. link Times cited: 69 Abstract: Due to their exceptional mechanical properties, thermal cond… read moreAbstract: Due to their exceptional mechanical properties, thermal conductivity and a wide band gap (5-6 eV), boron nitride nanotubes and nanosheets have promising applications in the field of engineering and biomedical science. Accurate modeling of failure or fracture in a nanomaterial inherently involves coupling of atomic domains of cracks and voids as well as a deformation mechanism originating from grain boundaries. This review highlights the recent progress made in the atomistic modeling of boron nitride nanofillers. Continuous improvements in computational power have made it possible to study the structural properties of these nanofillers at the atomistic scale. read less NOT USED (low confidence) E. Goharshadi and S. J. Mahdizadeh, “Thermal conductivity and heat transport properties of nitrogen-doped graphene.,” Journal of molecular graphics & modelling. 2015. link Times cited: 30 NOT USED (low confidence) Y. Gao, X. Zhang, Y. Jing, and M. Hu, “The unexpected non-monotonic inter-layer bonding dependence of the thermal conductivity of bilayered boron nitride.,” Nanoscale. 2015. link Times cited: 20 Abstract: Hexagonal boron nitride (BN) and its bilayer form are very f… read moreAbstract: Hexagonal boron nitride (BN) and its bilayer form are very fascinating two-dimensional materials that have attracted tremendous interest recently. Their realistic applications in emerging nanoelectronics usually quest for manipulating the thermal transport properties in a precise manner. Using nonequilibrium molecular dynamics simulations, we herein studied the effect of inter-layer covalent bonding on the thermal conductivity of bilayered BN. We found that the in-plane thermal conductivity of bilayered BN, which can be largely tuned by introducing covalent bonding between the two BN layers, depends not only on the inter-layer bonding density, but also on the detailed topological configuration of the inter-layer bonds. For randomly distributed inter-layer bonding the thermal conductivity of bilayered BN decreases monotonically with inter-layer bonding density, the same behavior already found for bilayered graphene. However, for regularly arranged inter-layer bonding the thermal conductivity of bilayered BN surprisingly possesses a non-monotonic dependence on the inter-layer bonding density. This non-intuitive non-monotonic dependence is further explained by performing spectral energy density analysis, where the peak and valley values of the thermal conductivity are governed by different mechanisms. These results suggest the application of inter-layer covalent bonding in designing nanoscale devices with precisely tunable thermal conductivities. read less NOT USED (low confidence) J. Lu, L. C. Gomes, R. W. Nunes, A. H. C. Neto, and K. Loh, “Lattice relaxation at the interface of two-dimensional crystals: graphene and hexagonal boron-nitride.,” Nano letters. 2014. link Times cited: 88 Abstract: Heteroepitaxy of two-dimensional (2D) crystals, such as hexa… read moreAbstract: Heteroepitaxy of two-dimensional (2D) crystals, such as hexagonal boron nitride (BN) on graphene (G), can occur at the edge of an existing heterointerface. Understanding strain relaxation at such 2D laterally fused interface is useful in fabricating heterointerfaces with a high degree of atomic coherency and structural stability. We use in situ scanning tunneling microscopy to study the 2D heteroepitaxy of BN on graphene edges on a Ru(0001) surface with the aim of understanding the propagation of interfacial strain. We found that defect-free, pseudomorphic growth of BN on a graphene edge "substrate" occurs only for a short distance (<1.29 nm) perpendicular to the interface, beyond which misfit zero-dimensional dislocations occur to reduce the elastic strain energy. Boundary states originating from a coherent zigzag-linked G/BN boundary are observed to greatly enhance the local conductivity, thus affording a new avenue to construct one-dimensional transport channels in G/BN hybrid interface. read less NOT USED (low confidence) M. Loeblein, R. Tay, S. H. Tsang, W. Ng, and E. Teo, “Configurable three-dimensional boron nitride-carbon architecture and its tunable electronic behavior with stable thermal performances.,” Small. 2014. link Times cited: 50 Abstract: Recent developments of 3D-graphene and 3D-boron-nitride have… read moreAbstract: Recent developments of 3D-graphene and 3D-boron-nitride have become of great interest owing to their potential for ultra-light flexible electronics. Here we demonstrate the first synthesis of novel 3D-BNC hybrids. By specifically controlling the compositions of C and BN, new fascinating properties are observed, such as highly tunable electrical conductivity, controllable EMI shielding properties, and stable thermal conductivity. This ultra-light hybrid opens up many new applications such as for electronic packaging and thermal interface materials (TIMs). read less NOT USED (low confidence) H. Zhan, Y. Wei, and Y. Gu, “Tuneable Resonance Properties of Graphene by Nitrogen-Dopant,” Applied Mechanics and Materials. 2014. link Times cited: 4 Abstract: Doping as one of the popular methods to manipulate the prope… read moreAbstract: Doping as one of the popular methods to manipulate the properties of nanomaterials has received extensive application in deriving different types of graphene derivates, while the understanding of the resonance properties of dopant graphene is still lacking in literature. Based on the large-scale molecular dynamics simulation, reactive empirical bond order potential, as well as the tersoff potential, the resonance properties of N-doped graphene were studied. The studied samples were established according to previous experiments with the N atom’s percentage ranging from 0.38%-2.93%, including three types of N dopant locations, i.e., graphitic N, pyrrolic N and pyridinic N. It is found that different percentages of N-dopant exert different influence to the resonance properties of the graphene, while the amount of N-dopant is not the only factor that determines its impact. For all the considered cases, a relative large percentage of N-dopant (2.65% graphitic N-dopant) is observed to introduce significant influence to the profile of the external energy, and thus lead to an extremely low Q-factor comparing with that of the pristine graphene. The most striking finding is that the natural frequency of the defective graphene with N-dopant’s percentage higher than 0.89% appears larger than its pristine counterpart. For the perfect graphene, the N-dopant shows larger influence to its natural frequency. This study will enrich the current understanding of the influence of dopants on graphene, which will eventually shed lights on the design of different molecules-doped graphene sheet. read less NOT USED (low confidence) Q. Tang and Z. Zhou, “Graphene-analogous low-dimensional materials,” Progress in Materials Science. 2013. link Times cited: 638 NOT USED (low confidence) G. Tong, F.-Y. Du, W.-hua Wu, R.-N. Wu, F. Liu, and Y.-Y. Liang, “Enhanced reactive oxygen species (ROS) yields and antibacterial activity of spongy ZnO/ZnFe2O4 hybrid micro-hexahedra selectively synthesized through a versatile glucose-engineered co-precipitation/annealing process.,” Journal of materials chemistry. B. 2013. link Times cited: 67 Abstract: In this study, sponge-like ZnO/ZnFe2O4 hybrid micro-hexahedr… read moreAbstract: In this study, sponge-like ZnO/ZnFe2O4 hybrid micro-hexahedra with diverse textures and compositions were fabricated by the thermal decomposition of hexahedral zinc/iron oxalate precursors, starting from a glucose-engineered co-precipitation process. The resulting ZnO/ZnFe2O4 micro-hexahedra were systematically characterized by X-ray powder diffraction, Fourier-transform infrared spectroscopy, scanning electronic microscopy, transmission electron microscopy (TEM), high-resolution TEM, and surface area analysis. Moreover, modulation in crystal size, composition, and textural properties of spongy ZnO/ZnFe2O4 micro-hexahedra was easily achieved by varying the Zn2+/Fe3+ feeding ratio and the annealing temperature. The antibacterial property of the products was analyzed by testing ATP (adenosine triphosphate) and inhibition zones. Results showed that oxidative stress was the governing mechanism for the antibacterial activity of ZnO/ZnFe2O4 hybrid materials. Moreover, we found that the higher reactive oxygen species yields and the resulting antibacterial activity were exhibited by the ZnO/ZnFe2O4 micro-hexahedra formed at lower sintering temperatures rather than the pure ZnO and Fe2O3. The enhanced antibacterial properties were likely caused by the spongy ZnO/ZnFe2O4 heterostructures, improving the probability of photoinduced charge separation and broadening the visible-light absorption. read less NOT USED (low confidence) T. Wu, Y.-he Xu, H. Wang, Z. Sun, and L. Zou, “Efficient and inexpensive preparation of graphene laminated film with ultrahigh thermal conductivity,” Carbon. 2021. link Times cited: 29 NOT USED (low confidence) T. Çagin, J. Haskins, A. Kinaci, and C. Sevik, “Thermal Transport for Nanostructured Materials.” 2021. link Times cited: 0 NOT USED (high confidence) H. Ouyang et al., “Kirigami-Inspired Thermal Regulator,” Physical Review Applied. 2023. link Times cited: 1 Abstract: One of the current challenges in nanoscience is tailoring ph… read moreAbstract: One of the current challenges in nanoscience is tailoring phononic devices, such as thermal regulators and thermal computing. This has long been a rather elusive task because the thermal-switching ratio is not as high as electronic analogs. Mapping from a topological kirigami assembly, nitrogen-doped porous graphene metamaterials on the nanoscale are inversely designed with a thermal-switching ratio of 27.79, which is more than double the value of previous work. We trace this behavior to the chiral folding-unfolding deformation, resulting in a metal-insulator transition. This study provides a nanomaterial design paradigm to bridge the gap between kinematics and functional metamaterials that motivates the development of high-performance thermal regulators. read less NOT USED (high confidence) S. Jubin, A. Rau, Y. Barsukov, S. Ethier, and I. Kaganovich, “Boron adatom adsorption on graphene: A case study in computational chemistry methods for surface interactions,” Frontiers of Physics. 2022. link Times cited: 4 Abstract: Though weak surface interactions and adsorption can play an … read moreAbstract: Though weak surface interactions and adsorption can play an important role in plasma processing and materials science, they are not necessarily simple to model. A boron adatom adsorbed on a graphene sheet serves as a case study for how carefully one must select the correct technique from a toolbox of computational chemistry methods. Using a variety of molecular dynamics potentials and density functional theory functionals, we evaluate the adsorption energy, investigate barriers to adsorption and migration, calculate corresponding reaction rates, and show that a surprisingly high level of theory may be necessary to verify that the system is described correctly. read less NOT USED (high confidence) R. Qi et al., “Measuring phonon dispersion at an interface,” Nature. 2021. link Times cited: 36 NOT USED (high confidence) Z. Xiong, L. Zhong, H. Wang, and X. Li, “Structural Defects, Mechanical Behaviors, and Properties of Two-Dimensional Materials,” Materials. 2021. link Times cited: 35 Abstract: Since the success of monolayer graphene exfoliation, two-dim… read moreAbstract: Since the success of monolayer graphene exfoliation, two-dimensional (2D) materials have been extensively studied due to their unique structures and unprecedented properties. Among these fascinating studies, the most predominant focus has been on their atomic structures, defects, and mechanical behaviors and properties, which serve as the basis for the practical applications of 2D materials. In this review, we first highlight the atomic structures of various 2D materials and the structural and energy features of some common defects. We then summarize the recent advances made in experimental, computational, and theoretical studies on the mechanical properties and behaviors of 2D materials. We mainly emphasized the underlying deformation and fracture mechanisms and the influences of various defects on mechanical behaviors and properties, which boost the emergence and development of topological design and defect engineering. We also further introduce the piezoelectric and flexoelectric behaviors of specific 2D materials to address the coupling between mechanical and electronic properties in 2D materials and the interactions between 2D crystals and substrates or between different 2D monolayers in heterostructures. Finally, we provide a perspective and outlook for future studies on the mechanical behaviors and properties of 2D materials. read less NOT USED (high confidence) M. Zojaji, A. Hydarinasab, S. Hashemabadi, and M. Mehranpour, “Rheological behaviour of shear thickening fluid of graphene oxide and SiO2 polyethylene glycol 400-based fluid with molecular dynamic simulation,” Molecular Simulation. 2021. link Times cited: 3 Abstract: ABSTRACT This study presents the influences of shear values … read moreAbstract: ABSTRACT This study presents the influences of shear values and temperature effects on shear thickening fluids by using the non-equilibrium molecular dynamic simulations. For this, the fluids were simulated with a low value of shear under constant temperature (300 K) and then the shear value increases to prepare thickening condition of the fluid. We calculate the viscosity of fluids with precise atomic arrangement via molecular dynamic approaches. In these methods, each atomic structure is represented by C, Si, O, and H atoms and an interatomic force field is implemented to describe their interactions. Molecular dynamic results show that, by increasing the inserted shear value, the viscosity of fluids increases and then decreases dramatically. The SiO2 atomic ratio variation shows that by increasing this physical parameter to 49.5%, the jamming viscosity reaches to 132.54 Pa.s. Furthermore, the temperature of the simulated system is a prominent parameter on the viscosity of the fluid and the jamming viscosity decreases to 37.24 Pa.s by increasing the temperature to 375 K. By increasing pressure in simulated structures, the jamming viscosity occurs with smaller rates. Finally, Rheological results show that, DREIDING and Universal force fields have the ability to simulate shear thickening fluids and correctly estimate their rheological behaviour. read less NOT USED (high confidence) F. Molaei, K. E. Eshkalak, S. Sadeghzadeh, and H. Siavoshi, “Hypersonic impact properties of pristine and hybrid single and multi-layer C3N and BC3 nanosheets,” Scientific Reports. 2020. link Times cited: 9 NOT USED (high confidence) W. Ouyang, O. Hod, and M. Urbakh, “Parity-Dependent Moiré Superlattices in Graphene/h-BN Heterostructures: A Route to Mechanomutable Metamaterials.,” Physical review letters. 2020. link Times cited: 11 Abstract: The superlattice of alternating graphene/h-BN few-layered he… read moreAbstract: The superlattice of alternating graphene/h-BN few-layered heterostructures is found to exhibit strong dependence on the parity of the number of layers within the stack. Odd-parity systems show a unique flamingolike pattern, whereas their even-parity counterparts exhibit regular hexagonal or rectangular superlattices. When the alternating stack consists of 7 layers or more, the flamingo pattern becomes favorable, regardless of parity. Notably, the out-of-plane corrugation of the system strongly depends on the shape of the superstructure resulting in significant parity dependence of its mechanical properties. The predicted phenomenon originates in an intricate competition between moiré patterns developing at the interface of consecutive layers. This mechanism is of general nature and is expected to occur in other alternating stacks of closely matched rigid layered materials as demonstrated for homogeneous alternating junctions of twisted graphene and h-BN. Our findings thus allow for the rational design of mechanomutable metamaterials based on van der Waals heterostructures. read less NOT USED (high confidence) N. R. Abdullah, H. Rashid, A. Manolescu, and V. Gudmundsson, “Interlayer interaction controlling the properties of AB- and AA-stacked bilayer graphene-like BC14n and si2c14,” Surfaces and Interfaces. 2020. link Times cited: 20 NOT USED (high confidence) V. Vijayaraghavan and L. Zhang, “Consistent Computational Modeling of Mechanical Properties of Carbon and Boron Nitride Nanotubes,” JOM. 2020. link Times cited: 7 NOT USED (high confidence) F. Thiemann, P. Rowe, E. A. Müller, and A. Michaelides, “Machine Learning Potential for Hexagonal Boron Nitride Applied to Thermally and Mechanically Induced Rippling,” The Journal of Physical Chemistry C. 2020. link Times cited: 18 Abstract: We introduce an interatomic potential for hexagonal boron ni… read moreAbstract: We introduce an interatomic potential for hexagonal boron nitride (hBN) based on the Gaussian approximation potential (GAP) machine learning methodology. The potential is based on a training set of... read less NOT USED (high confidence) W. Ouyang, H. Qin, M. Urbakh, and O. Hod, “Controllable Thermal Conductivity in Twisted Homogeneous Interfaces of Graphene and Hexagonal Boron Nitride,” Nano Letters. 2020. link Times cited: 41 Abstract: Thermal conductivity of homogeneous twisted stacks of graphi… read moreAbstract: Thermal conductivity of homogeneous twisted stacks of graphite is found to strongly depend on the misfit angle. The underlying mechanism relies on the angle dependence of phonon–phonon couplings across the twisted interface. Excellent agreement between the calculated thermal conductivity of narrow graphitic stacks and corresponding experimental results indicates the validity of the predictions. This is attributed to the accuracy of interlayer interaction descriptions obtained by the dedicated registry-dependent interlayer potential used. Similar results for h-BN stacks indicate overall higher conductivity and reduced misfit angle variation. This opens the way for the design of tunable heterogeneous junctions with controllable heat-transport properties ranging from substrate-isolation to efficient heat evacuation. read less NOT USED (high confidence) V. Choyal and S. I. Kundalwal, “Effect of Stone–Wales defects on the mechanical behavior of boron nitride nanotubes,” Acta Mechanica. 2020. link Times cited: 18 NOT USED (high confidence) V. Vijayaraghavan and L. Zhang, “Tensile Properties of Boron Nitride-Carbon Nanosheet-Reinforced Aluminum Nanocomposites Using Molecular Dynamics Simulation,” JOM. 2020. link Times cited: 9 NOT USED (high confidence) B. Zhang, Y. Liang, B. Liu, W. Liu, and Z. Liu, “Enhancing the Thermo-Mechanical Property of Polymer by Weaving and Mixing High Length–Diameter Ratio Filler,” Polymers. 2020. link Times cited: 1 Abstract: Improving thermo-mechanical characteristics of polymers can … read moreAbstract: Improving thermo-mechanical characteristics of polymers can efficiently promote their applications in heat exchangers and thermal management. However, a feasible way to enhance the thermo-mechanical property of bulk polymers at low filler content still remains to be explored. Here, we propose mixing high length-diameter ratio filler such as carbon nanotube (CNT), boron nitride (BN) nanotube, and copper (Cu) nanowire, in the woven polymer matrix to meet the purpose. Through molecular dynamics (MD) simulation, the thermal properties of three woven polymers including woven polyethylene (PE), woven poly (p-phenylene) (PPP), and woven polyacetylene (PA) are investigated. Besides, using woven PE as a polymer matrix, three polymer nanocomposites, namely PE-CNT, PE-BN, and PE-Cu, are constructed by mixing CNT, BN nanotube, and Cu nanowire respectively, whose thermo-mechanical characteristics are compared via MD simulation. Morphology and phonons spectra analysis are conducted to reveal the underlying mechanisms. Furthermore, impacts of electron-phonon coupling and electrical field on the thermal conductivity of PE-Cu are uncovered via two temperature model MD simulation. Classical theoretical models are modified to predict the effects of filler and matrix on the thermal conductivity of polymer nanocomposites. This work can provide useful guidelines for designing thermally conductive bulk polymers and polymer nanocomposites. read less NOT USED (high confidence) K. E. Eshkalak, S. Sadeghzadeh, and F. Molaei, “Aluminum nanocomposites reinforced with monolayer polyaniline (C3N): assessing the mechanical and ballistic properties,” RSC Advances. 2020. link Times cited: 9 Abstract: This study unveils C3N, a new material that serves as an exc… read moreAbstract: This study unveils C3N, a new material that serves as an excellent reinforcement to enhance the mechanical properties of aluminum using a molecular dynamics simulation method. Results show that the C3N nanosheets greatly improve the mechanical properties of aluminum-based nanocomposites. With only 1.3 wt% C3N, the Young's modulus, fracture strength, and fracture strain increased by 27, 70, and 51 percent, respectively. A comparison between the reinforcement of graphene and C3N in an aluminum (Al) matrix shows that in terms of the mechanical properties, the graphene–aluminum composite is weaker than the C3N–aluminum composite in the tensile tests, but slightly stronger in the energy adsorption tests. Our findings show that the mechanical properties are highly dependent on the strain rate and temperature. The effects of various imperfections, such as the vacancy, crack, and void defects, on the mechanical properties were also studied. Results show that in the presence of void defects, the structure exhibited higher mechanical properties than when there were other defects. This phenomenon was found to be related to the decrease in the effective load transfer from aluminum to C3N. Furthermore, by increasing the weight percent of the nanosheets up to 5%, the energy absorption rate increased by 25% compared to the pure aluminum. When C3N was placed on top of the aluminum surface, the silicon nanoparticles were associated with a 35% energy adsorption by the nanocomposite. The results of this paper could be used to help understand and overcome some limitations in the fabrication of metallic nanocomposites with 2D material reinforcement. read less NOT USED (high confidence) L. Razzaghi, M. Khalkhali, A. Rajabpour, and F. Khoeini, “Effect of graphene and carbon-nitride nanofillers on the thermal transport properties of polymer nanocomposites: A combined molecular dynamics and finite element study.,” Physical review. E. 2020. link Times cited: 8 Abstract: Low thermal conductivity of polymers, which is one of the co… read moreAbstract: Low thermal conductivity of polymers, which is one of the considerable drawbacks of commonly used composite structures, has been the focus of many researchers aiming to achieve high-performance polymer-based nanocomposites through the inclusion of highly thermally conductive fillers inside the polymer matrices. Thus, in the present study, a multiscale scheme using nonequilibrium molecular dynamics and the finite element method is developed to explore the impact of different nanosized fillers (carbon-nitride and graphene) on the effective thermal conductivity of polyethylene-based nanocomposites. We show that the thermal conductivity of amorphous polyethylene at room temperature using the reactive bond order interatomic potential is nearly 0.36±0.05W/mK. Also, the atomistic results predict that, compared to the C_{3}N and graphene nanosheets, the C_{2}N nanofilm presents a much stronger interfacial thermal conductance with polyethylene. Furthermore, the results indicate that the effective thermal conductivity values of C_{2}N-polyethylene, C_{3}N-polyethylene, and graphene-polyethylene nanocomposite, at constant volume fractions of 1%, are about 0.47, 0.56, and 0.74W/mK, respectively. In other words, the results of our models reveal that the thermal conductivity of fillers is the dominant factor that defines the effective thermal conductivity of nanocomposites. read less NOT USED (high confidence) Z. Wei, Z. Yang, M. Liu, H. Wu, Y. Chen, and F. Yang, “Thermal boundary conductance between high thermal conductivity boron arsenide and silicon,” Journal of Applied Physics. 2020. link Times cited: 4 Abstract: Thermal boundary conductance (TBC) is important for heat dis… read moreAbstract: Thermal boundary conductance (TBC) is important for heat dissipation in light-emitting diodes (LEDs). In this study, we predicted the TBC between the high thermal conductivity boron arsenide (BAs) and silicon (Si) by nonequilibrium molecular dynamics (MD) simulations. From the thermal conductivity accumulation function with respect to phonon frequency, the dominant phonon frequencies for heat conduction in BAs are extremely different from those in Si. However, our nonequilibrium MD simulations indicated that the TBC of the BAs/Si interface was still high compared to most other interfaces, even though there was a major frequency mismatch in the thermal conductivity accumulation function between BAs and Si. The primary reason for the high TBC is the overlap of phonon density of states between BAs and Si in the frequency range of 5–8 THz. The range of predicted TBC of the BAs/Si interface was between 200 and 300 MW/m2 K in the temperature range of 300–700 K, and the values of the TBC were not sensitive to the temperature. We also found that the TBCs in Si/BAs and Si/Ge interfaces were close to each other considering the simulation uncertainty. This work indicates BAs as an excellent material for heat dissipation across the interfaces. read less NOT USED (high confidence) Y. Nan, D. Tan, J. Zhao, M. Willatzen, and Z. L. Wang, “Shape- and size dependent piezoelectric properties of monolayer hexagonal boron nitride nanosheets,” Nanoscale Advances. 2019. link Times cited: 8 Abstract: We use molecular dynamics simulations (MD) to study piezoele… read moreAbstract: We use molecular dynamics simulations (MD) to study piezoelectric properties of hexagonal boron nitride nanosheets (BNNS) and reveal how piezoelectric properties depend on size and shape. We first analyze how the macroscopic shape affects the full 2D structure symmetry and its piezoelectric tensor. In particular, we demonstrate that a hexagonal (rectangular)-shaped BNNS belongs to the hexagonal 6̄m2 (monoclinic m) point group. Our simulation results show that the piezoelectric constants of BNNS depend strongly on the macroscopic shape, in agreement with the symmetry of the structure, but are nearly independent of the macroscopic size. The present study provides a detailed understanding of the piezoelectric properties of finite size BNNS and guidance to future experiments and optimization of 2D piezoelectric materials in general. read less NOT USED (high confidence) A. Senturk, A. Oktem, and A. E. S. Konukman, “Investigation of interfacial thermal resistance of hybrid graphene/hexagonal boron nitride,” International Journal of Mechanics and Materials in Design. 2019. link Times cited: 9 NOT USED (high confidence) V. Vijayaraghavan and L. Zhang, “Tensile and Interfacial Loading Characteristics of Boron Nitride-Carbon Nanosheet Reinforced Polymer Nanocomposites,” Polymers. 2019. link Times cited: 15 Abstract: The discovery of hybrid boron nitride–carbon (BN–C) nanostru… read moreAbstract: The discovery of hybrid boron nitride–carbon (BN–C) nanostructures has triggered enormous research interest in the design and fabrication of new generation nanocomposites. The robust design of these nanocomposites for target applications requires their mechanical strength to be characterized with a wide range of factors. This article presents a comprehensive study, with the aid of molecular dynamics analysis, of the tensile loading mechanics of BN–C nanosheet reinforced polyethylene (PE) nanocomposites. It is observed that the geometry and lattice arrangement of the BN–C nanosheet influences the tensile loading characteristics of the nanocomposites. Furthermore, defects in the nanosheet can severely impact the tensile loading resistance, the extent of which is determined by the defect’s location. This study also found that the tensile loading resistance of nanocomposites tends to weaken at elevated temperatures. The interfacial mechanics of the BN–C nanocomposites are also investigated. This analysis revealed a strong dependency with the carbon concentration in the BN–C nanosheet. read less NOT USED (high confidence) A. Jamr’oz and J. Majewski, “Morphology, Ordering, Stability, and Electronic Structure of Carbon‐Doped Hexagonal Boron Nitride,” physica status solidi (b). 2019. link Times cited: 6 Abstract: Theoretical studies of morphology, stability, and electronic… read moreAbstract: Theoretical studies of morphology, stability, and electronic structure of monolayer hexagonal CBN alloys with rich content of h‐BN and carbon concentration not exceeding 50% are presented. The studies are based on the bond order type of the valence force field to account for the interactions between atomic constituents and Monte Carlo method with Metropolis algorithm to establish equilibrium distribution of atoms over the lattice. It is found that the phase separation into graphene and h‐BN domains occurs in the majority of growth conditions. Only in N‐rich growth conditions, it is possible to obtain a quasi uniform distribution of carbon atoms over the boron sublattice. It is been predicted that the energy gap in stoichiometric Cx(BN)1−x alloys exhibits extremely strong bowing. read less NOT USED (high confidence) E. Kishor and N. Swaminathan, “A Molecular Dynamics Based Comparison of the Mechanical Properties of Three Polytypes of Cubic BC3,” Journal of Superhard Materials. 2019. link Times cited: 2 NOT USED (high confidence) A. Senturk, A. Oktem, and A. E. S. Konukman, “Investigation of interfacial thermal resistance of hybrid graphene/hexagonal boron nitride,” International Journal of Mechanics and Materials in Design. 2019. link Times cited: 0 NOT USED (high confidence) A. Senturk, A. Oktem, and A. E. S. Konukman, “An investigation on the thermo-mechanical properties of boron-doped g-C3N4,” Applied Physics A. 2019. link Times cited: 11 NOT USED (high confidence) S. Thomas, K. Ajith, S. U. Lee, and M. C. Valsakumar, “Assessment of the mechanical properties of monolayer graphene using the energy and strain-fluctuation methods,” RSC Advances. 2018. link Times cited: 28 Abstract: Molecular statics and dynamics simulations were performed to… read moreAbstract: Molecular statics and dynamics simulations were performed to investigate the mechanical properties of a monolayer graphene sheet using an efficient energy method and strain-fluctuation method. Using the energy method, we observed that the mechanical properties of an infinite graphene sheet are isotropic, whereas for a finite sheet, they are anisotropic. This work is the first to report the temperature-dependent elastic constants of graphene between 100 and 1000 K using the strain-fluctuation method. We found that the out-of-plane thermal excursions in a graphene membrane lead to strong anharmonic behavior, which allows large deviations from isotropic elasticity. The computed Young's modulus and Poisson's ratio of a sheet with an infinite spatial extent are 0.939 TPa and 0.223, respectively. We also found that graphene sheets with both finite and infinite spatial extent satisfy the Born elastic stability conditions. We extracted the variation in bending modulus with the system size at zero kelvin (0.83 eV) using a formula derived from the Foppl–von Karman approach. When the temperature increases, the Young's modulus of the sample decreases, which effectively reduces the longitudinal and shear wave velocities. read less NOT USED (high confidence) V. Vijayaraghavan and L. Zhang, “Effective Mechanical Properties and Thickness Determination of Boron Nitride Nanosheets Using Molecular Dynamics Simulation,” Nanomaterials. 2018. link Times cited: 37 Abstract: Research in boron nitride nanosheets (BNNS) has evoked signi… read moreAbstract: Research in boron nitride nanosheets (BNNS) has evoked significant interest in the field of nano-electronics, nanoelectromechanical (NEMS) devices, and nanocomposites due to its excellent physical and chemical properties. Despite this, there has been no reliable data on the effective mechanical properties of BNNS, with the literature reporting a wide scatter of strength data for the same material. To address this challenge, this article presents a comprehensive analysis on the effect of vital factors which can result in variations of the effective mechanical properties of BNNS. Additionally, the article also presents the computation of the correct wall thickness of BNNS from elastic theory equations, which is an important descriptor for any research to determine the mechanical properties of BNNS. It was predicted that the correct thickness of BNNS should be 0.106 nm and the effective Young’s modulus to be 2.75 TPa. It is anticipated that the findings from this study could provide valuable insights on the true mechanical properties of BNNS that could assist in the design and development of efficient BN-based NEMS devices, nanosensors, and nanocomposites. read less NOT USED (high confidence) B. Mortazavi, M. Makaremi, M. Shahrokhi, Z. Fan, and T. Rabczuk, “N-graphdiyne two-dimensional nanomaterials: Semiconductors with low thermal conductivity and high stretchability,” Carbon. 2018. link Times cited: 82 NOT USED (high confidence) Y. Hong, J. Zhang, and X. Zeng, “Monolayer and bilayer polyaniline C3N: two-dimensional semiconductors with high thermal conductivity.,” Nanoscale. 2018. link Times cited: 71 Abstract: Polyaniline (PANI) has been extensively studied in the past … read moreAbstract: Polyaniline (PANI) has been extensively studied in the past few decades owing to its broad applications in electronic devices. However, two dimensional PANI was not realized until very recently. In this work, the thermal transport properties of one of the newly synthesized 2D PANI structures, C3N, are systematically investigated using classical molecular dynamics simulations. The in-plane thermal conductivity (κ) of monolayer and bilayer C3N structures is computed, and the κ values for infinite-length systems are found to be as high as 820 and 805 W m-1 K-1, respectively. Both the values are markedly higher than those of many prevailing 2D semiconducting materials such as phosphorene, hexagonal boron nitride, MoS2 and MoSe2. The effects of different modulators, such as system dimension, temperature, interlayer coupling strength and tensile strain, on the calculated thermal conductivity are evaluated. Monotonic decreasing trends of thermal conductivity with temperature and tensile strain are found, while a positive correlation between the thermal conductivity and system dimension is revealed. Interlayer coupling strength is found to have negligible effects on the in-plane thermal conductivity of bilayer C3N. The cross-plane interfacial thermal resistance (R) between two adjacent C3N layers is evaluated in the temperature range from 100 to 500 K and at different coupling strengths. The predicted R at temperature 300 K equals 3.4 × 10-8 K m-2 W-1. The maximum reductions of R can amount to 59% and 68% with respect to temperature and coupling strength, respectively. Our results provide theoretical guidance to future applications of C3N-based low-dimensional materials in electronic devices. read less NOT USED (high confidence) H. Chakraborty, S. Mogurampelly, V. Yadav, U. Waghmare, and M. Klein, “Phonons and thermal conducting properties of borocarbonitride (BCN) nanosheets.,” Nanoscale. 2018. link Times cited: 12 Abstract: Hexagonal borocarbonitrides (BCN) are a class of 2D material… read moreAbstract: Hexagonal borocarbonitrides (BCN) are a class of 2D materials, which display excellent catalytic activity for water splitting. Here, we report the analysis of thermal stability, phonons and thermal conductivity of BCN monolayers over a wide range of temperatures using classical molecular dynamics simulations. Our results show that in contrast to the case of graphene and boron nitride monolayers, the out-of-plane phonons in BCN monolayers induce an asymmetry in the phonon density of states at all temperatures. Despite possessing lower thermal conducting properties compared to graphene and BN monolayers, the BCN nanosheets do not lose thermal conductivity as much as graphene and BN in the studied temperature range of 200-1000 K, and thus, BCN nanosheets are suitable for thermal interface device applications over a wide range of temperatures. Besides their promising role in water splitting, the above-mentioned results highlight the possibility of expanding the use of BCN 2D materials in thermal management applications and thermoelectrics. read less NOT USED (high confidence) T. Iwata and K. Shintani, “Reduction of the thermal conductivity of a graphene/hBN heterobilayer via interlayer sp3 bonds.,” Physical chemistry chemical physics : PCCP. 2018. link Times cited: 21 Abstract: Thermal conductivities (TCs) of graphene (g)/hexagonal boron… read moreAbstract: Thermal conductivities (TCs) of graphene (g)/hexagonal boron nitride (hBN) heterobilayers with interlayer sp3 bonds are computed using nonequilibrium molecular dynamics (NEMD) simulations. It is revealed that the TC of a g/hBN heterobilayer drastically decreases if there is even a few interlayer sp3 bonds, and continues to gradually decrease upon increasing their fraction up to 0.25, where the fraction of the interlayer sp3 bonds is defined by the atomic fraction of interlayer-sp3-bonded carbon atoms within graphene constituting a g/hBN heterobilayer. If their fraction exceeds 0.25, the TC of a g/hBN heterobilayer gradually increases, namely, the TC of a g/hBN heterobilayer takes a minimum at the fraction of 0.25 of the interlayer sp3 bonds. In order to understand such a behavior of the TC of the heterobilayer, the local phonon density of states (DOSs) in each of the two layers is calculated. By examining the local phonon DOSs, it was found that the existence of the minimum TC of the heterobilayer can be understood by considering both the phonon scattering and the characteristic change of the heterobilayer structure. In the range of the low fractions of interlayer sp3 bonds, the van der Waals (vdW) interactions are predominantly effective for binding the two layers, and the interlayer sp3 bonds act as phonon scatterers like defects to make the TC of the heterobilayer decrease. Upon increasing the fraction of interlayer sp3 bonds, the contribution of the interlayer sp3 bonds to the unification of the two layers becomes stronger, and hence the rigidity of the heterobilayer structure gradually increases. If their fraction exceeds 0.25, the heterobilayer structure approaches a quasi-three-dimensional one, so that the TC of the heterobilayer increases. These findings will be useful for tuning the TCs of g/hBN heterobilayers via interlayer sp3 bonds. read less NOT USED (high confidence) M. Z. Hossain, T. Hao, and B. Silverman, “Stillinger–Weber potential for elastic and fracture properties in graphene and carbon nanotubes,” Journal of Physics: Condensed Matter. 2018. link Times cited: 42 Abstract: This paper presents a new framework for determining the Stil… read moreAbstract: This paper presents a new framework for determining the Stillinger–Weber (SW) potential parameters for modeling fracture in graphene and carbon nanotubes. In addition to fitting the equilibrium material properties, the approach allows fitting the potential to the forcing behavior as well as the mechanical strength of the solid, without requiring ad hoc modification of the nearest-neighbor interactions for avoiding artificial stiffening of the lattice at larger deformation. Consistent with the first-principles results, the potential shows the Young’s modulus of graphene to be isotropic under symmetry-preserving and symmetry-breaking deformation conditions. It also shows the Young’s modulus of carbon nanotubes to be diameter-dependent under symmetry-breaking loading conditions. The potential addresses the key deficiency of existing empirical potentials in reproducing experimentally observed glass-like brittle fracture in graphene and carbon nanotubes. In simulating the entire deformation process leading to fracture, the SW-potential costs several factors less computational time compared to the state-of-the-art interatomic potentials that enables exploration of the fracture processes in large atomistic systems which are inaccessible otherwise. read less NOT USED (high confidence) L. M. Sandonas, G. Cuba-Supanta, R. Gutierrez, A. Dianat, C. Landauro, and G. Cuniberti, “Enhancement of thermal transport properties of asymmetric Graphene/hBN nanoribbon heterojunctions by substrate engineering,” Carbon. 2017. link Times cited: 23 NOT USED (high confidence) A. I. Khan, I. Navid, M. Noshin, and S. Subrina, “Thermal transport characterization of hexagonal boron nitride nanoribbons using molecular dynamics simulation,” AIP Advances. 2017. link Times cited: 28 Abstract: Due to similar atomic bonding and electronic structure to gr… read moreAbstract: Due to similar atomic bonding and electronic structure to graphene, hexagonal boron nitride (h-BN) has broad application prospects such as the design of next generation energy efficient nano-electronic devices. Practical design and efficient performance of these devices based on h-BN nanostructures would require proper thermal characterization of h-BN nanostructures. Hence, in this study we have performed equilibrium molecular dynamics (EMD) simulation using an optimized Tersoff-type interatomic potential to model the thermal transport of nanometer sized zigzag hexagonal boron nitride nanoribbons (h-BNNRs). We have investigated the thermal conductivity of h-BNNRs as a function of temperature, length and width. Thermal conductivity of h-BNNRs shows strong temperature dependence. With increasing width, thermal conductivity increases while an opposite pattern is observed with the increase in length. Our study on h-BNNRs shows considerably lower thermal conductivity compared to GNRs. To elucidate these aspect... read less NOT USED (high confidence) T. Han, F. Scarpa, and N. Allan, “Super stretchable hexagonal boron nitride Kirigami,” Thin Solid Films. 2017. link Times cited: 20 NOT USED (high confidence) X. Gu, Y. Wei, X. Yin, B. Li, and R. Yang, “Colloquium: Phononic thermal properties of two-dimensional materials,” Reviews of Modern Physics. 2017. link Times cited: 156 Abstract: Following the emergence of many novel two-dimensional (2-D) … read moreAbstract: Following the emergence of many novel two-dimensional (2-D) materials beyond graphene, interest has grown in exploring implications for fundamental physics and practical applications, ranging from electronics, photonics, phononics, to thermal management and energy storage. In this Colloquium, we first summarize and compare the phonon properties, such as phonon dispersion and relaxation time, of pristine 2-D materials with single layer graphene to understand the role of crystal structure and dimension on thermal conductivity. We then compare the phonon properties, contrasting idealized 2-D crystals, realistic 2-D crystals, and 3-D crystals, and synthesizing this to develop a physical picture of how the sample size of 2-D materials affects their thermal conductivity. The effects of geometry, such as number of layers, and nanoribbon width, together with the presence of defects, mechanical strain, and substrate interactions, on the thermal properties of 2-D materials are discussed. Intercalation affects both the group velocities and phonon relaxation times of layered crystals and thus tunes the thermal conductivity along both the through-plane and basal-plane directions. We conclude with a discussion of the challenges in theoretical and experimental studies of thermal transport in 2-D materials. The rich and special phonon physics in 2-D materials make them promising candidates for exploring novel phenomena such as topological phonon effects and applications such as phononic quantum devices. read less NOT USED (high confidence) C. D. da Silva and C. Amon, “Predicting phonon thermal transport in strained two-dimensional materials: Graphene, boron nitride, and molybdenum disulfide,” 2017 16th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm). 2017. link Times cited: 2 Abstract: Despite the extensive research done on two-dimensional mater… read moreAbstract: Despite the extensive research done on two-dimensional materials in recent years, little is still known about the physics of thermal energy carriers (phonons) at this low dimensionality, especially when these materials are stretched. In this work, we apply molecular dynamics simulations to estimate phonon relaxation times and thermal conductivities of strained samples of single-layer graphene, boron nitride, and molybdenum disulfide. Our results reveal that the thermal response of these 2D materials to tensile strain is considerably different, despite the similarities of their lattice structures. On the one hand, the thermal conductivity of boron nitride monotonically increases until 18% of strain is applied, approximately doubling the conductivity of an unstrained sample. On the other hand, the thermal conductivity of graphene first increases by roughly 30% until 8% of strain is applied, and then it sharply decreases for higher percentages of strain. In contrast, the conductivity of molybdenum disulfide drops dramatically in response to percentages of strain as small as 2%. These thermal responses are addressed here in the context of the phonon properties of these materials, with particular emphasis on the role of the acoustic phonon modes. read less NOT USED (high confidence) B. Mortazavi, “Ultra high stiffness and thermal conductivity of graphene like C3N,” Carbon. 2017. link Times cited: 217 NOT USED (high confidence) S. Lu and A. McGaughey, “Thermal conductance of graphene/hexagonal boron nitride heterostructures,” Journal of Applied Physics. 2017. link Times cited: 16 Abstract: The lattice-based scattering boundary method is applied to c… read moreAbstract: The lattice-based scattering boundary method is applied to compute the phonon mode-resolved transmission coefficients and thermal conductances of in-plane heterostructures built from graphene and hexagonal boron nitride (hBN). The thermal conductance of all structures is dominated by acoustic phonon modes near the Brillouin zone center that have high group velocity, population, and transmission coefficient. Out-of-plane modes make their most significant contributions at low frequencies, whereas in-plane modes contribute across the frequency spectrum. Finite-length superlattice junctions between graphene and hBN leads have a lower thermal conductance than comparable junctions between two graphene leads due to lack of transmission in the hBN phonon bandgap. The thermal conductances of bilayer systems differ by less than 10% from their single-layer counterparts on a per area basis, in contrast to the strong thermal conductivity reduction when moving from single- to multi-layer graphene. read less NOT USED (high confidence) J. E. Barrios-Vargas et al., “Electrical and Thermal Transport in Coplanar Polycrystalline Graphene-hBN Heterostructures.,” Nano letters. 2017. link Times cited: 61 Abstract: We present a theoretical study of electronic and thermal tra… read moreAbstract: We present a theoretical study of electronic and thermal transport in polycrystalline heterostructures combining graphene (G) and hexagonal boron nitride (hBN) grains of varying size and distribution. By increasing the hBN grain density from a few percent to 100%, the system evolves from a good conductor to an insulator, with the mobility dropping by orders of magnitude and the sheet resistance reaching the MΩ regime. The Seebeck coefficient is suppressed above 40% mixing, while the thermal conductivity of polycrystalline hBN is found to be on the order of 30-120 Wm-1 K-1. These results, agreeing with available experimental data, provide guidelines for tuning G-hBN properties in the context of two-dimensional materials engineering. In particular, while we proved that both electrical and thermal properties are largely affected by morphological features (e.g., by the grain size and composition), we find in all cases that nanometer-sized polycrystalline G-hBN heterostructures are not good thermoelectric materials. read less NOT USED (high confidence) M.-Q. Le and Y. Umeno, “Fracture of monolayer boronitrene and its interface with graphene,” International Journal of Fracture. 2017. link Times cited: 24 NOT USED (high confidence) B. Mortazavi, O. Rahaman, T. Rabczuk, and L. Pereira, “Thermal conductivity and mechanical properties of nitrogenated holey graphene,” Carbon. 2016. link Times cited: 111 NOT USED (high confidence) S. Thomas, K. Ajith, and M. C. Valsakumar, “Directional anisotropy, finite size effect and elastic properties of hexagonal boron nitride,” Journal of Physics: Condensed Matter. 2016. link Times cited: 43 Abstract: Classical molecular dynamics simulations have been performed… read moreAbstract: Classical molecular dynamics simulations have been performed to analyze the elastic and mechanical properties of two-dimensional (2D) hexagonal boron nitride (h-BN) using a Tersoff-type interatomic empirical potential. We present a systematic study of h-BN for various system sizes. Young’s modulus and Poisson’s ratio are found to be anisotropic for finite sheets whereas they are isotropic for the infinite sheet. Both of them increase with system size in accordance with a power law. It is concluded from the computed values of elastic constants that h-BN sheets, finite or infinite, satisfy Born’s criterion for mechanical stability. Due to the the strong in-plane sp2 bonds and the small mass of boron and nitrogen atoms, h-BN possesses high longitudinal and shear velocities. The variation of bending rigidity with system size is calculated using the Foppl–von Karman approach by coupling the in-plane bending and out-of-plane stretching modes of the 2D h-BN. read less NOT USED (high confidence) Z. Bai, L. Zhang, and L. Liu, “Improving low-energy boron/nitrogen ion implantation in graphene by ion bombardment at oblique angles.,” Nanoscale. 2016. link Times cited: 31 Abstract: Ion implantation is a widely adopted approach to structurall… read moreAbstract: Ion implantation is a widely adopted approach to structurally modify graphene and tune its electrical properties for a variety of applications. Further development of the approach requires a fundamental understanding of the mechanisms that govern the ion bombardment process as well as establishment of key relationships between the controlling parameters and the dominant physics. Here, using molecular dynamics simulations with adaptive bond order calculations, we demonstrate that boron and nitrogen ion bombardment at oblique angles (particularly at 70°) can improve both the productivity and quality of perfect substitution by over 25%. We accomplished this by systematically analyzing the effects of the incident angle and ion energy in determining the probabilities of six distinct types of physics that may occur in an ion bombardment event, including reflection, absorption, substitution, single vacancy, double vacancy, and transmission. By analyzing the atomic trajectories from 576,000 simulations, we identified three single vacancy creation mechanisms and four double vacancy creation mechanisms, and quantified their probability distributions in the angle-energy space. These findings further open the door for improved control of ion implantation towards a wide range of applications of graphene. read less NOT USED (high confidence) S. Sarikurt et al., “Tailoring thermal conductivity of silicon/germanium nanowires utilizing core-shell architecture,” Journal of Applied Physics. 2016. link Times cited: 10 Abstract: Low-dimensional nanostructured materials show large variatio… read moreAbstract: Low-dimensional nanostructured materials show large variations in their thermal transport properties. In this work, we investigate the influence of the core-shell architecture on nanowire (1D) thermal conductivity and evaluate its validity as a strategy to achieve a better thermoelectric performance. To obtain the thermal conductivity values, equilibrium molecular dynamics simulations are conducted for core-shell nanowires of silicon and germanium. To explore the parameter space, we have calculated thermal conductivity values of the Si-core/Ge-shell and Ge-core/Si-shell nanowires having different cross-sectional sizes and core contents at several temperatures. Our results indicate that (1) increasing the cross-sectional area of pristine Si and pristine Ge nanowires increases the thermal conductivity, (2) increasing the Ge core size in the Ge-core/Si-shell structure results in a decrease in the thermal conductivity at 300 K, (3) the thermal conductivity of the Si-core/Ge-shell nanowires demonstrates a mini... read less NOT USED (high confidence) M. Biswas and B. Knigge, “Opportunities and Challenges of Atomistic Modeling to Simulate Amorphous Carbon Properties for Computer Hard-Disk Applications,” IEEE Transactions on Magnetics. 2016. link Times cited: 1 Abstract: Amorphous carbon is used as coating material for computer ha… read moreAbstract: Amorphous carbon is used as coating material for computer hard-disks magnetic media and recording heads. There has been significant improvement in understanding amorphous carbon's properties based on experimental observations. High data storage density requirement in the coming years necessitates the use of an ultrathin carbon overcoat while maintaining or enhancing its tribological, thermal, optical, and corrosion properties for better recording performance and reliability. Along with experimental techniques, atomistic simulations can be a useful tool to provide fundamental understanding, especially in the cases where experiments are not adequate. This review gives an overview of how atomistic modeling can provide insights into amorphous carbon properties and discuss challenges for such modeling. read less NOT USED (high confidence) J. Zhang, W. Xie, J. Zhao, and S. Zhang, “Band alignment of two-dimensional lateral heterostructures,” 2D Materials. 2016. link Times cited: 74 Abstract: Recent experimental synthesis of two-dimensional (2D) hetero… read moreAbstract: Recent experimental synthesis of two-dimensional (2D) heterostructures opens a door to new opportunities in tailoring the electronic properties for novel 2D devices. Here, we show that a wide range of lateral 2D heterostructures could have a prominent advantage over the traditional three-dimensional (3D) heterostructures, because their band alignments are insensitive to the interfacial conditions. They should be at the Schottky–Mott limits for semiconductor–metal junctions and at the Anderson limits for semiconductor junctions, respectively. This fundamental difference from the 3D heterostructures is rooted in the fact that, in the asymptotic limit of large distance, the effect of the interfacial dipole vanishes for 2D systems. Due to the slow decay of the dipole field and the dependence on the vacuum thickness, however, studies based on first-principles calculations often failed to reach such a conclusion. Taking graphene/hexagonal-BN and MoS2/WS2 lateral heterostructures as the respective prototypes, we show that the converged junction width can be order of magnitude longer than that for 3D junctions. The present results provide vital guidance to high-quality transport devices wherever a lateral 2D heterostructure is involved. read less NOT USED (high confidence) A. Chandra, P. Patra, and B. Bhattacharya, “Thermal vibration characteristics of armchair boron-nitride nanotubes,” Journal of Applied Physics. 2015. link Times cited: 8 Abstract: A nanomechanical resonator based sensor works by detecting s… read moreAbstract: A nanomechanical resonator based sensor works by detecting small changes in the natural frequency of the device in presence of external agents. In this study, we address the length and the temperature-dependent sensitivity of precompressed armchair Boron-Nitride nanotubes towards their use as sensors. The vibrational data, obtained using molecular dynamics simulations, are analyzed for frequency content through the fast Fourier transformation. As the temperature of the system rises, the vibrational spectrum becomes noisy, and the modal frequencies show a red-shift irrespective of the length of the nanotube, suggesting that the nanotube based sensors calibrated at a particular temperature may not function desirably at other temperatures.Temperature-inducednoise becomes increasingly pronounced with the decrease in the length of the nanotube. For the shorter nanotube at higher temperatures, we observe multiple closely spaced peaks near the natural frequency, that create a masking effect and reduce the sensitivity of detection. However, longer nanotubes do not show these spurious frequencies, and are considerably more sensitive than the shorter ones. read less NOT USED (high confidence) T. Han, Y. Luo, and C. Wang, “Effects of SI, N and B Doping on the Mechanical Properties of Graphene Sheets,” Acta Mechanica Solida Sinica. 2015. link Times cited: 15 NOT USED (high confidence) Z. Guo, T. Chang, X. Guo, and H. Gao, “Gas-like adhesion of two-dimensional materials onto solid surfaces,” Scientific Reports. 2015. link Times cited: 18 NOT USED (high confidence) Q. Xiong and X. Tian, “Torsional properties of hexagonal boron nitride nanotubes, carbon nanotubes and their hybrid structures: A molecular dynamics study,” AIP Advances. 2015. link Times cited: 15 Abstract: The torsional mechanical properties of hexagonal single-wall… read moreAbstract: The torsional mechanical properties of hexagonal single-walled boron nitride nanotubes (SWBNNTs), single-walled carbon nanotubes (SWCNTs), and their hybrid structures (SWBN-CNTs) are investigated using molecular dynamics (MD) simulation. Two approaches - force approach and energy approach, are adopted to calculate the shear moduli of SWBNNTs and SWCNTs, the discrepancy between two approaches is analyzed. The results show that the shear moduli of single-walled nanotubes (SWNTs), including SWBNNTs and SWCNTs are dependent on the diameter, especially for armchair SWNTs. The armchair SWNTs show the better ability of resistance the twisting comparable to the zigzag SWNTs. The effects of diameter and length on the critical values of torque of SWNTs are obtained by comparing the torsional behaviors of SWNTs with different diameters and different lengths. It is observed that the MD results of the effect of diameter and length on the critical values of torque agrees well with the prediction of continuum shell mode... read less NOT USED (high confidence) X. Qi-lin, L. Zhenhuan, and T. Xiaogeng, “The defect-induced fracture behaviors of hexagonal boron-nitride monolayer nanosheets under uniaxial tension,” Journal of Physics D: Applied Physics. 2015. link Times cited: 42 Abstract: Due to its excellent mechanical and electrical insulating pr… read moreAbstract: Due to its excellent mechanical and electrical insulating properties, the hexagonal boron-nitride (h-BN) monolayer nanosheet is regarded as a complementary addition to graphene. However, its mechanical strength can be significantly affected by various defects pre-existing in it, such as a Stone–Wales defect, a vacancy defect, an atomic anti-site defect, etc. In this work, the influences of various pre-existing defects on the fracture behaviors of an h-BN monolayer nanosheet are investigated carefully using molecular dynamics simulation. The results show that the nucleation and evolution of a fracture induced by defects in the h-BN monolayer nanosheet are directional, and that the crack always starts from the location which has a weak bond energy. An unexpected observation is that the defect propagates mostly in the zigzag direction but occasionally in the armchair direction. The fracture strength and the fracture strain of the h-BN monolayer nanosheet are reduced at different extents due to the various pre-existing defects. Additionally, for the defective h-BN monolayer nanosheets, the fracture strength and strain measured in the armchair direction is much higher than the strength found in the zigzag direction. However, the strengths measured in the armchair and zigzag directions for the defect-free h-BN monolayer nanosheets almost are identical which implies that the armchair direction has a stronger ability to resist various defects compared to the zigzag direction. read less NOT USED (high confidence) C. Zhang and S. Chen, “Defect- and dopant-controlled carbon nanotubes fabricated by self-assembly of graphene nanoribbons,” Nano Research. 2015. link Times cited: 7 NOT USED (high confidence) S. Thomas, K. Ajith, S. Chandra, and M. C. Valsakumar, “Temperature dependent structural properties and bending rigidity of pristine and defective hexagonal boron nitride,” Journal of Physics: Condensed Matter. 2015. link Times cited: 58 Abstract: Structural and thermodynamical properties of monolayer prist… read moreAbstract: Structural and thermodynamical properties of monolayer pristine and defective boron nitride sheets (h-BN) have been investigated in a wide temperature range by carrying out atomistic simulations using a tuned Tersoff-type inter-atomic empirical potential. The temperature dependence of lattice parameter, radial distribution function, specific heat at constant volume, linear thermal expansion coefficient and the height correlation function of the thermally excited ripples on pristine as well as defective h-BN sheet have been investigated. Specific heat shows considerable increase beyond the Dulong–Petit limit at high temperatures, which is interpreted as a signature of strong anharmonicity present in h-BN. Analysis of the height fluctuations, ⟨h2⟩ ?>, shows that the bending rigidity and variance of height fluctuations are strongly temperature dependent and this is explained using the continuum theory of membranes. A detailed study of the height–height correlation function shows deviation from the prediction of harmonic theory of membranes as a consequence of the strong anharmonicity in h-BN. It is also seen that the variance of the height fluctuations increases with defect concentration. read less NOT USED (high confidence) P. Pokatashkin, A. Kuksin, and A. Yanilkin, “Angular dependent potential for α-boron and large-scale molecular dynamics simulations,” Modelling and Simulation in Materials Science and Engineering. 2015. link Times cited: 9 Abstract: Both quantum mechanical and molecular-dynamics (MD) simulati… read moreAbstract: Both quantum mechanical and molecular-dynamics (MD) simulations of α-boron are done at this work. Angular dependent interatomic potential (ADP) for boron is obtained using force-matching technique. Fitting data are based on ab initio results within −20..100 GPa pressure range and temperatures up to 2000 K. Characteristics of α-boron, obtained using ADP potential such as bond lengths at equilibrium condition, bulk modulus, pressure-volume relations, Gruneisen coefficient, thermal expansion coefficient are in good agreement with both ab initio data, obtained in this work and known experimental data. As an example of application, the propagation of shock waves through a single crystal of α-boron is also explored by large-scale MD simulations. read less NOT USED (high confidence) J. Zhang, Y. Hong, and Y. Yue, “Thermal transport across graphene and single layer hexagonal boron nitride,” Journal of Applied Physics. 2015. link Times cited: 118 Abstract: As the dimensions of nanocircuits and nanoelectronics shrink… read moreAbstract: As the dimensions of nanocircuits and nanoelectronics shrink, thermal energies are being generated in more confined spaces, making it extremely important and urgent to explore for efficient heat dissipation pathways. In this work, the phonon energy transport across graphene and hexagonal boron-nitride (h-BN) interface is studied using classic molecular dynamics simulations. Effects of temperature, interatomic bond strength, heat flux direction, and functionalization on interfacial thermal transport are investigated. It is found out that by hydrogenating graphene in the hybrid structure, the interfacial thermal resistance (R) between graphene and h-BN can be reduced by 76.3%, indicating an effective approach to manipulate the interfacial thermal transport. Improved in-plane/out-of-plane phonon couplings and broadened phonon channels are observed in the hydrogenated graphene system by analyzing its phonon power spectra. The reported R results monotonically decrease with temperature and interatomic bond strengths. No thermal rectification phenomenon is observed in this interfacial thermal transport. Results reported in this work give the fundamental knowledge on graphene and h-BN thermal transport and provide rational guidelines for next generation thermal interface material designs. read less NOT USED (high confidence) P. Dollfus, V. H. Nguyen, and J. Saint-Martin, “Thermoelectric effects in graphene nanostructures,” Journal of Physics: Condensed Matter. 2015. link Times cited: 143 Abstract: The thermoelectric properties of graphene and graphene nanos… read moreAbstract: The thermoelectric properties of graphene and graphene nanostructures have recently attracted significant attention from the physics and engineering communities. In fundamental physics, the analysis of Seebeck and Nernst effects is very useful in elucidating some details of the electronic band structure of graphene that cannot be probed by conductance measurements alone, due in particular to the ambipolar nature of this gapless material. For applications in thermoelectric energy conversion, graphene has two major disadvantages. It is gapless, which leads to a small Seebeck coefficient due to the opposite contributions of electrons and holes, and it is an excellent thermal conductor. The thermoelectric figure of merit ZT of a two-dimensional (2D) graphene sheet is thus very limited. However, many works have demonstrated recently that appropriate nanostructuring and bandgap engineering of graphene can concomitantly strongly reduce the lattice thermal conductance and enhance the Seebeck coefficient without dramatically degrading the electronic conductance. Hence, in various graphene nanostructures, ZT has been predicted to be high enough to make them attractive for energy conversion. In this article, we review the main results obtained experimentally and theoretically on the thermoelectric properties of graphene and its nanostructures, emphasizing the physical effects that govern these properties. Beyond pure graphene structures, we discuss also the thermoelectric properties of some hybrid graphene structures, as graphane, layered carbon allotropes such as graphynes and graphdiynes, and graphene/hexagonal boron nitride heterostructures which offer new opportunities. Finally, we briefly review the recent activities on other atomically thin 2D semiconductors with finite bandgap, i.e. dichalcogenides and phosphorene, which have attracted great attention for various kinds of applications, including thermoelectrics. read less NOT USED (high confidence) N. Krishnan and D. Ghosh, “Chirality dependent elastic properties of single-walled boron nitride nanotubes under uniaxial and torsional loading,” Journal of Applied Physics. 2014. link Times cited: 25 Abstract: The elastic behavior of single-walled boron nitride nanotube… read moreAbstract: The elastic behavior of single-walled boron nitride nanotubes is studied under axial and torsional loading. Molecular dynamics simulation is carried out with a tersoff potential for modeling the interatomic interactions. Different chiral configurations with similar diameter are considered to study the effect of chirality on the elastic and shear moduli. Furthermore, the effects of tube length on elastic modulus are also studied by considering different aspects ratios. It is observed that both elastic and shear moduli depend upon the chirality of a nanotube. For aspect ratios less than 15, the elastic modulus reduces monotonically with an increase in the chiral angle. For chiral nanotubes, the torsional response shows a dependence on the direction of loading. The difference between the shear moduli against and along the chiral twist directions is maximum for chiral angle of 15°, and zero for zigzag (0°) and armchair (30°) configurations. read less NOT USED (high confidence) T. Han, Y. Luo, and C. Wang, “Effects of temperature and strain rate on the mechanical properties of hexagonal boron nitride nanosheets,” Journal of Physics D: Applied Physics. 2014. link Times cited: 106 Abstract: The effect of temperature and strain rate on mechanical prop… read moreAbstract: The effect of temperature and strain rate on mechanical properties remains an open topic in research of hexagonal boron nitride (h-BN) nanosheets. To examine these fundamental issues we have performed molecular dynamics simulations to record the stress–strain curves in tensile tests and measure Young's modulus, fracture strength and fracture strain in armchair and zigzag directions. Comparing the results obtained at different temperatures and strain rates we have quantified the effects of the two factors on the tensile properties of the h-BN nanosheets. The influence of crystal orientation is also examined in the present study. It is found that the h-BN nanosheets are basically an anisotropic material whose tensile properties vary substantially with temperature and strain rate. In particular, a yielding platform is observed for the h-BN nanomaterial at relatively low temperature. read less NOT USED (high confidence) S. Zhao and J. Xue, “Mechanical properties of hybrid graphene and hexagonal boron nitride sheets as revealed by molecular dynamic simulations,” Journal of Physics D: Applied Physics. 2013. link Times cited: 124 Abstract: Molecular dynamic simulations are performed to investigate t… read moreAbstract: Molecular dynamic simulations are performed to investigate the mechanical properties of hybrid graphene and hexagonal boron nitrogen (h-BN) sheet with the concentration of BN ranging from 0% to 100%. We find that Young's modulus of the hybrid sheet decreases with increasing concentration of BN, irrespective of BN shapes and distributions. However, a little mixing of h-BN and graphene can result in a noticeable drop in the yield strength of the hybrid sheet. In addition, the hybrid sheet exhibits strong plasticity behaviour during the tensile loading, which is not observed in pure graphene and BN sheets. We further demonstrate that this behaviour can be interpreted by the fact that the interface between the BN domain and graphene governs the failure mechanism of the hybrid sheet, which can be approximated by the classical Griffith model. Our results suggest that the mechanical properties of the hybrid graphene–BN sheet should be considered carefully when evaluating its whole performance when it is used in bandgap-engineered applications such as electronics and optics. read less NOT USED (high confidence) J. Yeo, “Modeling and simulation of the structural evolution and thermal properties of ultralight aerogel and 2D materials.” 2014. link Times cited: 1 |
 Tersoff_LAMMPS_KinaciHaskinsSevik_2012_BNC__MO_105008013807_000
Tersoff_LAMMPS_KinaciHaskinsSevik_2012_BNC__MO_105008013807_000