EAM_Dynamo_FarkasCaro_2020_FeNiCrCoAl__MO_820335782779_000
Interatomic potential for Aluminum (Al), Chromium (Cr), Cobalt (Co), Iron (Fe), Nickel (Ni).
Use this Potential
Use this Potential
| Title
A single sentence description.
|
EAM potential (LAMMPS cubic hermite tabulation) for the Fe-Ni-Cr-Co-Al system developed by Farkas and Caro (2020) v000 |
|---|---|
| Description
A short description of the Model describing its key features including for example: type of model (pair potential, 3-body potential, EAM, etc.), modeled species (Ac, Ag, ..., Zr), intended purpose, origin, and so on.
|
This is a set of embedded atom model (EAM) interatomic potentials developed to represent highly idealized face-centered cubic (FCC) mixtures of Fe–Ni–Cr–Co–Al at near-equiatomic compositions. Potential functions for the transition metals and their crossed interactions are taken from previous work for Fe–Ni–Cr–Co–Cu [D. Farkas and A. Caro: J. Mater. Res. 33 (19), 3218–3225, 2018], while cross-pair interactions involving Al were developed using a mix of the component pair functions fitted to known intermetallic properties. The resulting heats of mixing of all binary equiatomic random FCC mixtures not containing Al is low, but significant short-range ordering appears in those containing Al, driven by a large atomic size difference. |
| Species
The supported atomic species.
| Al, Co, Cr, Fe, Ni |
| Disclaimer
A statement of applicability provided by the contributor, informing users of the intended use of this KIM Item.
|
None |
| Content Origin | https://www.ctcms.nist.gov/potentials/entry/2020--Farkas-D-Caro-A--Fe-Ni-Cr-Co-Al/ |
| Contributor |
I Nikiforov |
| Maintainer |
I Nikiforov |
| Developer |
Diana Farkas A. Caro |
| Published on KIM | 2022 |
| How to Cite |
This Model originally published in [1] is archived in OpenKIM [2-5]. [1] Farkas D, Caro A. Model interatomic potentials for Fe–Ni–Cr–Co–Al high-entropy alloys. Journal of Materials Research [Internet]. 2020Nov1;35(22):3031–40. Available from: https://doi.org/10.1557/jmr.2020.294 doi:10.1557/jmr.2020.294 — (Primary Source) A primary source is a reference directly related to the item documenting its development, as opposed to other sources that are provided as background information. [2] Farkas D, Caro A. EAM potential (LAMMPS cubic hermite tabulation) for the Fe-Ni-Cr-Co-Al system developed by Farkas and Caro (2020) v000. OpenKIM; 2022. doi:10.25950/8c495c7e [3] Foiles SM, Baskes MI, Daw MS, Plimpton SJ. EAM Model Driver for tabulated potentials with cubic Hermite spline interpolation as used in LAMMPS v005. OpenKIM; 2018. doi:10.25950/68defa36 [4] Tadmor EB, Elliott RS, Sethna JP, Miller RE, Becker CA. The potential of atomistic simulations and the Knowledgebase of Interatomic Models. JOM. 2011;63(7):17. doi:10.1007/s11837-011-0102-6 [5] Elliott RS, Tadmor EB. Knowledgebase of Interatomic Models (KIM) Application Programming Interface (API). OpenKIM; 2011. doi:10.25950/ff8f563a Click here to download the above citation in BibTeX format. |
| Citations
This panel presents information regarding the papers that have cited the interatomic potential (IP) whose page you are on. The OpenKIM machine learning based Deep Citation framework is used to determine whether the citing article actually used the IP in computations (denoted by "USED") or only provides it as a background citation (denoted by "NOT USED"). For more details on Deep Citation and how to work with this panel, click the documentation link at the top of the panel. The word cloud to the right is generated from the abstracts of IP principle source(s) (given below in "How to Cite") and the citing articles that were determined to have used the IP in order to provide users with a quick sense of the types of physical phenomena to which this IP is applied. The bar chart shows the number of articles that cited the IP per year. Each bar is divided into green (articles that USED the IP) and blue (articles that did NOT USE the IP). Users are encouraged to correct Deep Citation errors in determination by clicking the speech icon next to a citing article and providing updated information. This will be integrated into the next Deep Citation learning cycle, which occurs on a regular basis. OpenKIM acknowledges the support of the Allen Institute for AI through the Semantic Scholar project for providing citation information and full text of articles when available, which are used to train the Deep Citation ML algorithm. |
This panel provides information on past usage of this interatomic potential (IP) powered by the OpenKIM Deep Citation framework. The word cloud indicates typical applications of the potential. The bar chart shows citations per year of this IP (bars are divided into articles that used the IP (green) and those that did not (blue)). The complete list of articles that cited this IP is provided below along with the Deep Citation determination on usage. See the Deep Citation documentation for more information. 
72 Citations (61 used)
Help us to determine which of the papers that cite this potential actually used it to perform calculations. If you know, click the .
USED (low confidence) W. Li et al., “Unraveling the two-stage precipitation mechanism in a hierarchical-structured fcc/L21 high-entropy alloy: Experiments and analytical modeling,” Acta Materialia. 2024. link Times cited: 0 USED (low confidence) J. Qu et al., “Molecular dynamics and first-principles calculations on the wetting behavior and mechanism of molten Al on nickel-infiltrated steel: A cross-scale simulation,” Computational Materials Science. 2024. link Times cited: 0 USED (low confidence) H. Dong et al., “TRIP-TWIP effect in deformation mechanisms of Co–Cr–Ni medium entropy via molecular dynamics simulations,” Journal of Materials Research and Technology. 2023. link Times cited: 0 USED (low confidence) L. Liu, Y. Zhang, Z. Zhang, J. Li, W. Jiang, and L. Sun, “Nanoprecipitate and stacking fault-induced high strength and ductility in a multiscale heterostructured high-entropy alloy,” International Journal of Plasticity. 2023. link Times cited: 0 USED (low confidence) Y. Liu et al., “Exploring the effects of temperature on the mechanical properties of high-entropy alloy (CoCrFeNiAl0.1) based on molecular dynamics simulation,” Modelling and Simulation in Materials Science and Engineering. 2023. link Times cited: 0 Abstract: In order to further explore the influence of temperature on … read more USED (low confidence) Q. Xu, X. Yuan, J. Eckert, and D. Şopu, “Crack-healing mechanisms in high-entropy alloys under ion irradiation,” Acta Materialia. 2023. link Times cited: 0 USED (low confidence) M. Moradi-Ganjeh, A. Farzadi, and A. Ramazani, “Atomic scale melting/solidification behavior and structural evolutions of AlCoCrFeNi high-entropy alloy during selective laser melting process,” Journal of Materials Research and Technology. 2023. link Times cited: 0 USED (low confidence) J. Kong, G. Luo, Y. Tian, and C. Du, “Atomic insight into tribological behavior of AlCoCrFeNi high entropy alloy at various nanoscratching conditions,” Journal of Materials Research and Technology. 2023. link Times cited: 0 USED (low confidence) H.-G. Nguyen and T.-H. Fang, “Mechanics of AlCuNiTi alloy orthogonal micro-cutting,” Modelling and Simulation in Materials Science and Engineering. 2023. link Times cited: 0 Abstract: The mechanical behavior of AlCuNiTi alloy during orthogonal … read more USED (low confidence) J. Kong, Q. Fang, and J. Li, “Optimizing the friction behavior of medium entropy alloy via controllable coherent nanoprecipitation,” Modelling and Simulation in Materials Science and Engineering. 2023. link Times cited: 0 Abstract: In recent years, FeCrNi medium entropy alloy, a new material… read more USED (low confidence) S. Barman and S. Dey, “Probing the mechanical and deformation behaviour of CNT-reinforced AlCoCrFeNi high-entropy alloy – a molecular dynamics approach,” Molecular Simulation. 2023. link Times cited: 0 Abstract: ABSTRACT This present study investigates the mechanical and … read more USED (low confidence) Q. Guo, H. Hou, K. Wang, M. Li, P. K. Liaw, and Y.-hui Zhao, “Coalescence of Al_0.3CoCrFeNi polycrystalline high-entropy alloy in hot-pressed sintering: a molecular dynamics and phase-field study,” npj Computational Materials. 2023. link Times cited: 1 USED (low confidence) K. Gan, D. Yan, Y. Zhang, and P. Niu, “Atomic insights into the effects of Al element on the nanoindentation behavior of single-crystal FeNiCoCr-based multicomponent alloys,” Materials Today Communications. 2023. link Times cited: 0 USED (low confidence) V.-T. Pham et al., “Effects of microstructure and vibration parameters on mechanical properties of nanoimprinted FeNiCrCoCu high-entropy alloys,” Physica B: Condensed Matter. 2023. link Times cited: 1 USED (low confidence) H.-G. Nguyen and T.-H. Fang, “Plastic deformation in nanoindentation of Alx(CuCrFeNi)1-x high entropy alloy,” Journal of Alloys and Compounds. 2023. link Times cited: 0 USED (low confidence) Z. Zhang, Q. Huang, and H. Zhou, “High-entropy alloy nanocrystals with low-angle grain boundary for superb plastic deformability and recoverability,” International Journal of Plasticity. 2023. link Times cited: 3 USED (low confidence) A. Liang, D. C. Goodelman, A. Hodge, D. Farkas, and P. S. Branicio, “CoFeNiTi and CrFeNiTi high entropy alloy thin films microstructure formation,” Acta Materialia. 2023. link Times cited: 1 USED (low confidence) G. Li et al., “Symbiotically engineered crystalline-amorphous nanostructure in a strong-yet-stable Al alloy with large twinning-induced plasticity,” Acta Materialia. 2023. link Times cited: 0 USED (low confidence) X. Lu et al., “Effect of Intragranular Solute Atom Segregation on the Mechanical Properties of the Ni–Co Alloy,” The Journal of Physical Chemistry C. 2023. link Times cited: 0 USED (low confidence) J. Jiang, W. Sun, N. Luo, and P. Chen, “Atomic-scale analysis of deformation behavior of face-centered cubic nanocrystalline high-entropy alloys with different grain sizes at high strain rates,” Materials Chemistry and Physics. 2023. link Times cited: 2 USED (low confidence) H. Deng et al., “Temperature dependence of the deformation behavior and mechanical response of CoCrNi medium-entropy alloy: experiment and simulation,” Journal of Materials Research and Technology. 2023. link Times cited: 0 USED (low confidence) D. Dinh-Quan, “Dependence of mechanical and surface characteristics on twin boundaries of CoCrFeNiAl high-entropy alloy,” Physica E: Low-dimensional Systems and Nanostructures. 2023. link Times cited: 0 USED (low confidence) “Discovery of new Fe2Ni2CrAlx multi-principal elements alloy with promising mechanical properties,” Journal of Materials Research and Technology. 2023. link Times cited: 0 USED (low confidence) T.-N. Vu, V.-T. Pham, and T. Fang, “Effects of structure and strain rate on deformation mechanism of twin lamellar Al0.3CoCrFeNi alloys,” Journal of Alloys and Compounds. 2023. link Times cited: 2 USED (low confidence) L. Qiao and J. Zhu, “Unveiling the compressive behavior of Fe2Ni2CrAl high entropy alloy: A combined molecular dynamics and finite element study,” Materials Today Communications. 2023. link Times cited: 3 USED (low confidence) Y. Bai, G. Lyu, Y. Wang, T. Chen, K. Zhang, and B. Wei, “Laser shock peening strengthens additively manufactured high-entropy alloy through novel surface grain rotation,” Materials Science and Engineering: A. 2023. link Times cited: 3 USED (low confidence) N. Tuchinda and C. Schuh, “Triple junction solute segregation in Al-based polycrystals,” Physical Review Materials. 2023. link Times cited: 3 USED (low confidence) D. Sur et al., “An Experimental High-Throughput to High-Fidelity Study Towards Discovering Al–Cr Containing Corrosion-Resistant Compositionally Complex Alloys,” High Entropy Alloys & Materials. 2023. link Times cited: 4 USED (low confidence) L. Qiao, R. Ramanujan, and J. Zhu, “Uncovering wear mechanism of a Fe2Ni2CrAl multi-principal elements alloy,” Journal of Materials Science. 2023. link Times cited: 1 USED (low confidence) R. Wang et al., “Molecular dynamics simulation of effects of Al on the evolution of displacement cascades in Al CoCrFeNi high entropy alloys,” Journal of Nuclear Materials. 2023. link Times cited: 1 USED (low confidence) D. Zhang, G. Zhang, H. Yu, W. Lv, K.-S. Wen, and H. Xu, “Controlling interfacial composition and improvement in bonding strength of compound casted Al/steel bimetal via Cr interlayer,” Journal of Materials Research and Technology. 2023. link Times cited: 1 USED (low confidence) Z. Zhao and J. Liu, “Probing Plastic Mechanisms in Gradient Dual-Phase High-Entropy Alloys Under Nanoindentation,” SSRN Electronic Journal. 2023. link Times cited: 1 USED (low confidence) Y. Li et al., “Plasticity Improvement in a Co-Rich Co40Fe25Cr20Ni15 High-Entropy Alloy via Al Alloying,” Materials. 2023. link Times cited: 3 Abstract: The mechanical properties of high-entropy alloys (HEAs) can … read more USED (low confidence) P. Sreeramagiri, P. Sharma, C. Das, and G. Balasubramanian, “Examining solid-state sintering of AlCoCrFeNi multi-principal element alloy by molecular simulations,” Computational Materials Science. 2023. link Times cited: 1 USED (low confidence) Z.-ming Yang et al., “Amorphization activated by semicoherent interfaces of FCC/BCC HEA multilayers during deformation,” Materials & Design. 2023. link Times cited: 4 USED (low confidence) D.-Q. Doan, V.-H. Nguyen, T.-V. Tran, and M.-T. Hoàng, “Atomic-scale analysis of mechanical and wear characteristics of AlCoCrFeNi high entropy alloy coating on Ni substrate,” Journal of Manufacturing Processes. 2023. link Times cited: 6 USED (low confidence) B. Waters, D. S. Karls, I. Nikiforov, R. Elliott, E. Tadmor, and B. Runnels, “Automated determination of grain boundary energy and potential-dependence using the OpenKIM framework,” Computational Materials Science. 2022. link Times cited: 5 USED (low confidence) R. Babicheva et al., “Effect of short-range ordering and grain boundary segregation on shear deformation of CoCrFeNi high-entropy alloys with Al addition,” Computational Materials Science. 2022. link Times cited: 13 USED (low confidence) Y. Lu and T. Fang, “Buckling instability and compressive deformation of Ni-Co-Cr medium-entropy alloy nanotubes,” Modelling and Simulation in Materials Science and Engineering. 2022. link Times cited: 2 Abstract: The aspect ratio has a significant effect on buckling instab… read more USED (low confidence) D. Yan, Z. Yun, and J. Li, “Twin boundary spacing and loading direction dependent tensile deformation of nano-twinned Al10(CrCoFeNi)90 high-entropy alloy: An atomic study,” International Journal of Mechanical Sciences. 2022. link Times cited: 7 USED (low confidence) U. Hecht et al., “Microstructure Evolution in the Hypo-Eutectic Alloy Al0.75crfeni2.1 Manufactured by Laser Powder Bed Fusion and Subsequent Annealing,” SSRN Electronic Journal. 2022. link Times cited: 1 USED (low confidence) Q. Wang, B. Wang, W. Yuan, and B. Gu, “Probing the crystal structure and dislocation evolution in single crystal Al0.3CoCrFeNi high-entropy alloy under nanoindentation,” Materials Today Communications. 2022. link Times cited: 9 USED (low confidence) Z. Zhao and J. Liu, “On Cyclic Plasticity of Nanostructured Dual-Phase Cocrfenial High-Entropy Alloy: An Atomistic Study,” SSRN Electronic Journal. 2022. link Times cited: 0 Abstract: In this study, we have employed molecular dynamics simulatio… read more USED (low confidence) L. J. Yuan, R. Tao, P. Wen, J. Li, S. Wang, and D. Li, “Molecular dynamics simulation of chemical short-range order strengthening in FCC FeNiCrCoAl alloys,” Physica B: Condensed Matter. 2022. link Times cited: 4 USED (low confidence) Q. Fang, W. Lu, Y. Chen, H. Feng, P. Liaw, and J. Li, “Hierarchical multiscale crystal plasticity framework for plasticity and strain hardening of multi-principal element alloys,” Journal of the Mechanics and Physics of Solids. 2022. link Times cited: 8 USED (low confidence) J. Kong, Y. Tian, X. Zeng, B. Liu, Q. Fang, and J. Li, “Friction and wear behavior of a precipitation-hardened equiatomic FeCrNi medium entropy alloy unraveled by molecular dynamics simulation,” Journal of Materials Research. 2022. link Times cited: 2 Abstract: The precipitation-hardened medium/high entropy alloys (MEAs/… read more USED (low confidence) N. Zhang, K. Gan, and Z. Li, “Atomistic insights on the deformation mechanisms of Cox(CrNi)100-x multicomponent alloys: The effect of Co content,” Computational Materials Science. 2022. link Times cited: 6 USED (low confidence) J. Jiang, W. Sun, and N. Luo, “Atomic insights into effects of temperature and grain diameter on the micro-deformation mechanism, mechanical properties and sluggish diffusion of nanocrystalline high-entropy alloys,” Materials Today Communications. 2022. link Times cited: 4 USED (low confidence) J. Chen, Y. Ding, X. Zhang, Y. Gao, and Y. Ma, “Intrinsic stacking fault energy and mechanism for deformation twin formation of solid solution matrix in Ni-based superalloys,” Vacuum. 2022. link Times cited: 5 USED (low confidence) Q. Xu, D. Şopu, X. Yuan, D. Kiener, and J. Eckert, “Interface-related deformation phenomena in metallic glass/high entropy nanolaminates,” Acta Materialia. 2022. link Times cited: 8 USED (low confidence) Y. Zhao, Q. Song, H. Ji, W. Cai, Z. Liu, and Y. Cai, “Multi-scale modeling method for polycrystalline materials considering grain boundary misorientation angle,” Materials & Design. 2022. link Times cited: 3 USED (low confidence) J. Jiang, W. Sun, and N. Luo, “Molecular dynamics study of microscopic deformation mechanism and tensile properties in AlxCoCrFeNi amorphous high-entropy alloys,” Materials Today Communications. 2022. link Times cited: 8 USED (low confidence) J. Li, X. Yang, P. Wang, and Q. An, “Dynamic interactions between low-angle grain boundary and stacking fault tetrahedron in Ni-Fe solid solution alloys,” Journal of Alloys and Compounds. 2022. link Times cited: 7 USED (low confidence) M. Abere et al., “A predictive analytical model of thermal conductivity for aluminum/transition metal high-entropy alloys,” Scripta Materialia. 2022. link Times cited: 6 USED (low confidence) Y. Lu, M.-P. Chang, and T. Fang, “Phase transformation and microstructure evolution of nanoimprinted NiCoCr medium entropy alloys,” Journal of Alloys and Compounds. 2022. link Times cited: 6 USED (low confidence) A. Jarlöv et al., “Molecular dynamics study on the strengthening mechanisms of Cr-Fe-Co-Ni high-entropy alloys based on the generalized stacking fault energy,” Journal of Alloys and Compounds. 2022. link Times cited: 29 USED (low confidence) D. E. Farache, J. C. Verduzco, Z. D. McClure, S. Desai, and A. Strachan, “Active learning and molecular dynamics simulations to find high melting temperature alloys,” Computational Materials Science. 2021. link Times cited: 9 USED (low confidence) J. Jiang et al., “Microstructural evolution and mechanical properties of AlxCoCrFeNi high-entropy alloys under uniaxial tension: A molecular dynamics simulations study,” Materials today communications. 2021. link Times cited: 21 USED (low confidence) D.-Q. Doan, T. Fang, and T.-H. Chen, “Microstructure and composition dependence of mechanical characteristics of nanoimprinted AlCoCrFeNi high-entropy alloys,” Scientific Reports. 2021. link Times cited: 32 USED (low confidence) A. A. Hasan et al., “Effects of aluminum content on thermoelectric performance of AlxCoCrFeNi high-entropy alloys,” Journal of Alloys and Compounds. 2021. link Times cited: 10 USED (low confidence) X. Liu et al., “A statistics-based study and machine-learning of stacking fault energies in HEAs,” Journal of Alloys and Compounds. 2023. link Times cited: 0 NOT USED (low confidence) R. Luo, B. Wang, Q. Wang, J. Yu, and Z. Gao, “Cyclic Degradation Mechanisms of Al0.3CoCrFeNi High-entropy Alloy under Different Loading Rates,” Materials Today Communications. 2023. link Times cited: 0 NOT USED (low confidence) A. Anand, S.-J. Liu, and C. V. Singh, “Recent advances in computational design of structural multi-principal element alloys,” iScience. 2023. link Times cited: 1 NOT USED (low confidence) Q. Guo et al., “Hardening-softening of Al0.3CoCrFeNi high-entropy alloy under nanoindentation,” Materials & Design. 2023. link Times cited: 27 NOT USED (low confidence) Y.-F. Wu, W. Yu, and S. Shen, “Developing a variable charge potential for Hf/Nb/Ta/Ti/Zr/O system via machine learning global optimization,” Materials & Design. 2023. link Times cited: 1 NOT USED (low confidence) Y. Tong et al., “Microstructure and deformation mechanism of dual-phase Al0.5CoCrNiFe high-entropy alloy,” Rare Metals. 2023. link Times cited: 0 NOT USED (low confidence) H. Zhao et al., “The fabrication and growth mechanism of AlCrFeCoNiCu0.5 HEA thin films by substrate-biased cathodic arc deposition,” Scientific Reports. 2023. link Times cited: 7 NOT USED (low confidence) T.-N. Vu, V.-T. Pham, and T. Fang, “Influences of grain size, temperature, and strain rate on mechanical properties of Al0.3CoCrFeNi high–entropy alloys,” Materials Science and Engineering: A. 2022. link Times cited: 6 NOT USED (low confidence) S. Singh et al., “Small-scale deformation behaviour of the AlCoCrFeNi2.1 eutectic high entropy alloy,” Philosophical Magazine. 2022. link Times cited: 1 Abstract: ABSTRACT Novel methods to probe and evaluate the mechanical … read more NOT USED (low confidence) Z. Sun, C. Shi, L. Gao, S. Lin, and W. Li, “Thermal physical properties of high entropy alloy Al0.3CoCrFeNi at elevated temperatures,” Journal of Alloys and Compounds. 2022. link Times cited: 18 NOT USED (high confidence) K. Choudhary, B. L. DeCost, L. Major, K. Butler, J. Thiyagalingam, and F. Tavazza, “Unified Graph Neural Network Force-field for the Periodic Table for Solids,” Digital Discovery. 2022. link Times cited: 6 Abstract: Classical force fields (FF) based on machine learning (ML) m… read more NOT USED (high confidence) L. Zhang, H. Xin, D. Zhao, Z. Li, and S. Ma, “Effect of Twin Boundary Density on Mechanical Behavior of Al0.1CoCrFeNi High-Entropy Alloy by Molecular Dynamics Simulation,” Frontiers in Materials. 2022. link Times cited: 1 Abstract: Molecular dynamics simulation method was used to study the i… read more |
| Funding |
Award Number: 1507846 Funder: Division of Materials Research |
| Short KIM ID
The unique KIM identifier code.
| MO_820335782779_000 |
| Extended KIM ID
The long form of the KIM ID including a human readable prefix (100 characters max), two underscores, and the Short KIM ID. Extended KIM IDs can only contain alpha-numeric characters (letters and digits) and underscores and must begin with a letter.
| EAM_Dynamo_FarkasCaro_2020_FeNiCrCoAl__MO_820335782779_000 |
| DOI |
10.25950/8c495c7e https://doi.org/10.25950/8c495c7e https://commons.datacite.org/doi.org/10.25950/8c495c7e |
| KIM Item Type
Specifies whether this is a Portable Model (software implementation of an interatomic model); Portable Model with parameter file (parameter file to be read in by a Model Driver); Model Driver (software implementation of an interatomic model that reads in parameters).
| Portable Model using Model Driver EAM_Dynamo__MD_120291908751_005 |
| Driver | EAM_Dynamo__MD_120291908751_005 |
| KIM API Version | 2.2 |
| Potential Type | eam |
(Click here to learn more about Verification Checks)
| Grade | Name | Category | Brief Description | Full Results | Aux File(s) |
|---|---|---|---|---|---|
| P | vc-species-supported-as-stated | mandatory | The model supports all species it claims to support; see full description. |
Results | Files |
| P | vc-periodicity-support | mandatory | Periodic boundary conditions are handled correctly; see full description. |
Results | Files |
| P | vc-permutation-symmetry | mandatory | Total energy and forces are unchanged when swapping atoms of the same species; see full description. |
Results | Files |
| B | vc-forces-numerical-derivative | consistency | Forces computed by the model agree with numerical derivatives of the energy; see full description. |
Results | Files |
| F | vc-dimer-continuity-c1 | informational | The energy versus separation relation of a pair of atoms is C1 continuous (i.e. the function and its first derivative are continuous); see full description. |
Results | Files |
| P | vc-objectivity | informational | Total energy is unchanged and forces transform correctly under rigid-body translation and rotation; see full description. |
Results | Files |
| P | vc-inversion-symmetry | informational | Total energy is unchanged and forces change sign when inverting a configuration through the origin; see full description. |
Results | Files |
| P | vc-memory-leak | informational | The model code does not have memory leaks (i.e. it releases all allocated memory at the end); see full description. |
Results | Files |
| P | vc-thread-safe | mandatory | The model returns the same energy and forces when computed in serial and when using parallel threads for a set of configurations. Note that this is not a guarantee of thread safety; see full description. |
Results | Files |
| P | vc-unit-conversion | mandatory | The model is able to correctly convert its energy and/or forces to different unit sets; see full description. |
Results | Files |
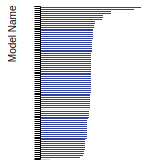
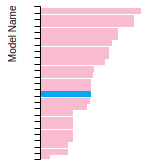
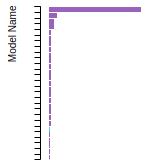
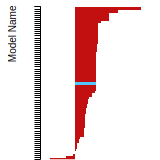
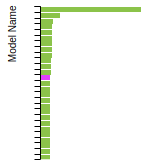
BCC Lattice Constant
This bar chart plot shows the mono-atomic body-centered cubic (bcc) lattice constant predicted by the current model (shown in the unique color) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
Species: Al
Species: Ni
Species: Fe
Species: Co
Species: Cr
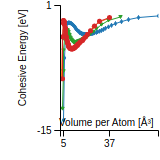
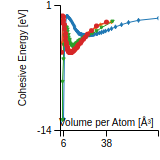
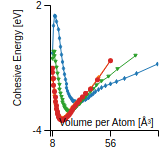
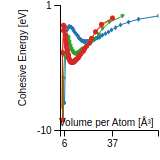
Cohesive Energy Graph
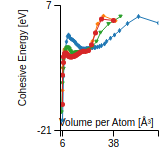
This graph shows the cohesive energy versus volume-per-atom for the current mode for four mono-atomic cubic phases (body-centered cubic (bcc), face-centered cubic (fcc), simple cubic (sc), and diamond). The curve with the lowest minimum is the ground state of the crystal if stable. (The crystal structure is enforced in these calculations, so the phase may not be stable.) Graphs are generated for each species supported by the model.
Species: Ni
Species: Co
Species: Al
Species: Cr
Species: Fe
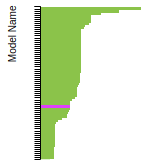
Diamond Lattice Constant
This bar chart plot shows the mono-atomic face-centered diamond lattice constant predicted by the current model (shown in the unique color) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
Species: Co
Species: Fe
Species: Al
Species: Cr
Species: Ni
Dislocation Core Energies
This graph shows the dislocation core energy of a cubic crystal at zero temperature and pressure for a specific set of dislocation core cutoff radii. After obtaining the total energy of the system from conjugate gradient minimizations, non-singular, isotropic and anisotropic elasticity are applied to obtain the dislocation core energy for each of these supercells with different dipole distances. Graphs are generated for each species supported by the model.
(No matching species)FCC Elastic Constants
This bar chart plot shows the mono-atomic face-centered cubic (fcc) elastic constants predicted by the current model (shown in blue) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
Species: Cr
Species: Fe
Species: Al
Species: Co
Species: Ni
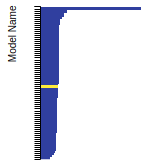
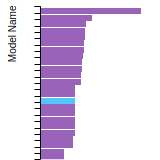
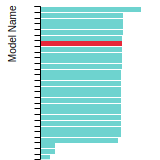
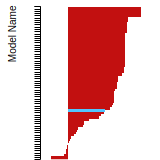
FCC Lattice Constant
This bar chart plot shows the mono-atomic face-centered cubic (fcc) lattice constant predicted by the current model (shown in red) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
Species: Co
Species: Al
Species: Fe
Species: Cr
Species: Ni
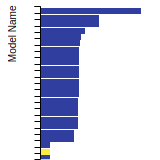
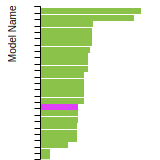
FCC Stacking Fault Energies
This bar chart plot shows the intrinsic and extrinsic stacking fault energies as well as the unstable stacking and unstable twinning energies for face-centered cubic (fcc) predicted by the current model (shown in blue) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
Species: Ni
Species: Al
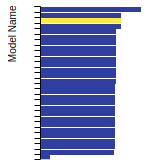
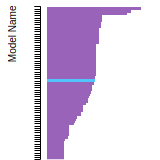
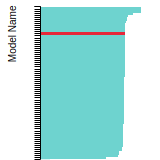
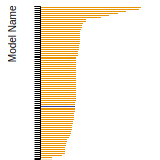
FCC Surface Energies
This bar chart plot shows the mono-atomic face-centered cubic (fcc) relaxed surface energies predicted by the current model (shown in blue) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
Species: Ni
Species: Al
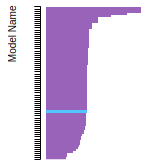
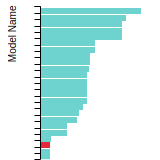
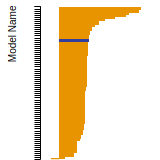
SC Lattice Constant
This bar chart plot shows the mono-atomic simple cubic (sc) lattice constant predicted by the current model (shown in the unique color) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
Species: Co
Species: Fe
Species: Cr
Species: Al
Species: Ni
Cubic Crystal Basic Properties Table
Species: AlSpecies: Co
Species: Cr
Species: Fe
Species: Ni
Cohesive energy versus lattice constant curve for monoatomic cubic lattices v003
Creators:
Contributor: karls
Publication Year: 2019
DOI: https://doi.org/10.25950/64cb38c5
This Test Driver uses LAMMPS to compute the cohesive energy of a given monoatomic cubic lattice (fcc, bcc, sc, or diamond) at a variety of lattice spacings. The lattice spacings range from a_min (=a_min_frac*a_0) to a_max (=a_max_frac*a_0) where a_0, a_min_frac, and a_max_frac are read from stdin (a_0 is typically approximately equal to the equilibrium lattice constant). The precise scaling and number of lattice spacings sampled between a_min and a_0 (a_0 and a_max) is specified by two additional parameters passed from stdin: N_lower and samplespacing_lower (N_upper and samplespacing_upper). Please see README.txt for further details.
Creators:
Contributor: karls
Publication Year: 2019
DOI: https://doi.org/10.25950/64cb38c5
This Test Driver uses LAMMPS to compute the cohesive energy of a given monoatomic cubic lattice (fcc, bcc, sc, or diamond) at a variety of lattice spacings. The lattice spacings range from a_min (=a_min_frac*a_0) to a_max (=a_max_frac*a_0) where a_0, a_min_frac, and a_max_frac are read from stdin (a_0 is typically approximately equal to the equilibrium lattice constant). The precise scaling and number of lattice spacings sampled between a_min and a_0 (a_0 and a_max) is specified by two additional parameters passed from stdin: N_lower and samplespacing_lower (N_upper and samplespacing_upper). Please see README.txt for further details.
Elastic constants for arbitrary crystals at zero temperature and pressure v000
Creators:
Contributor: ilia
Publication Year: 2024
DOI: https://doi.org/10.25950/888f9943
Computes the elastic constants for an arbitrary crystal. A robust computational protocol is used, attempting multiple methods and step sizes to achieve an acceptably low error in numerical differentiation and deviation from material symmetry. The crystal structure is specified using the AFLOW prototype designation as part of the Crystal Genome testing framework. In addition, the distance from the obtained elasticity tensor to the nearest isotropic tensor is computed.
Creators:
Contributor: ilia
Publication Year: 2024
DOI: https://doi.org/10.25950/888f9943
Computes the elastic constants for an arbitrary crystal. A robust computational protocol is used, attempting multiple methods and step sizes to achieve an acceptably low error in numerical differentiation and deviation from material symmetry. The crystal structure is specified using the AFLOW prototype designation as part of the Crystal Genome testing framework. In addition, the distance from the obtained elasticity tensor to the nearest isotropic tensor is computed.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Elastic constants for AlCo in AFLOW crystal prototype A13B4_oP102_31_17a11b_8a2b at zero temperature and pressure v000 | view | 527883 | |
| Elastic constants for CrFe in AFLOW crystal prototype A2B_cF24_227_c_b at zero temperature and pressure v000 | view | 187070 | |
| Elastic constants for CrNi in AFLOW crystal prototype A2B_cF24_227_c_b at zero temperature and pressure v000 | view | 189057 | |
| Elastic constants for FeNi in AFLOW crystal prototype A2B_cF24_227_c_b at zero temperature and pressure v000 | view | 99100 | |
| Elastic constants for AlNi in AFLOW crystal prototype A3B2_hP5_164_ad_d at zero temperature and pressure v000 | view | 155242 |
Elastic constants for cubic crystals at zero temperature and pressure v006
Creators: Junhao Li and Ellad Tadmor
Contributor: tadmor
Publication Year: 2019
DOI: https://doi.org/10.25950/5853fb8f
Computes the cubic elastic constants for some common crystal types (fcc, bcc, sc, diamond) by calculating the hessian of the energy density with respect to strain. An estimate of the error associated with the numerical differentiation performed is reported.
Creators: Junhao Li and Ellad Tadmor
Contributor: tadmor
Publication Year: 2019
DOI: https://doi.org/10.25950/5853fb8f
Computes the cubic elastic constants for some common crystal types (fcc, bcc, sc, diamond) by calculating the hessian of the energy density with respect to strain. An estimate of the error associated with the numerical differentiation performed is reported.
Equilibrium structure and energy for a crystal structure at zero temperature and pressure v002
Creators:
Contributor: ilia
Publication Year: 2024
DOI: https://doi.org/10.25950/2f2c4ad3
Computes the equilibrium crystal structure and energy for an arbitrary crystal at zero temperature and applied stress by performing symmetry-constrained relaxation. The crystal structure is specified using the AFLOW prototype designation. Multiple sets of free parameters corresponding to the crystal prototype may be specified as initial guesses for structure optimization. No guarantee is made regarding the stability of computed equilibria, nor that any are the ground state.
Creators:
Contributor: ilia
Publication Year: 2024
DOI: https://doi.org/10.25950/2f2c4ad3
Computes the equilibrium crystal structure and energy for an arbitrary crystal at zero temperature and applied stress by performing symmetry-constrained relaxation. The crystal structure is specified using the AFLOW prototype designation. Multiple sets of free parameters corresponding to the crystal prototype may be specified as initial guesses for structure optimization. No guarantee is made regarding the stability of computed equilibria, nor that any are the ground state.
Relaxed energy as a function of tilt angle for a symmetric tilt grain boundary within a cubic crystal v002
Creators: Brandon Runnels
Contributor: brunnels
Publication Year: 2019
DOI: https://doi.org/10.25950/4723cee7
Computes grain boundary energy for a range of tilt angles given a crystal structure, tilt axis, and material.
Creators: Brandon Runnels
Contributor: brunnels
Publication Year: 2019
DOI: https://doi.org/10.25950/4723cee7
Computes grain boundary energy for a range of tilt angles given a crystal structure, tilt axis, and material.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Relaxed energy as a function of tilt angle for a 111 symmetric tilt grain boundary in bcc Fe v000 | view | 19311555 | |
| Relaxed energy as a function of tilt angle for a 112 symmetric tilt grain boundary in bcc Fe v000 | view | 113741285 | |
| Relaxed energy as a function of tilt angle for a 110 symmetric tilt grain boundary in fcc Fe v000 | view | 19177529 | |
| Relaxed energy as a function of tilt angle for a 111 symmetric tilt grain boundary in fcc Fe v000 | view | 23371408 | |
| Relaxed energy as a function of tilt angle for a 112 symmetric tilt grain boundary in fcc Fe v000 | view | 77092622 | |
| Relaxed energy as a function of tilt angle for a 112 symmetric tilt grain boundary in fcc Ni v000 | view | 36802895 |
Relaxed energy as a function of tilt angle for a symmetric tilt grain boundary within a cubic crystal v003
Creators:
Contributor: brunnels
Publication Year: 2022
DOI: https://doi.org/10.25950/2c59c9d6
Computes grain boundary energy for a range of tilt angles given a crystal structure, tilt axis, and material.
Creators:
Contributor: brunnels
Publication Year: 2022
DOI: https://doi.org/10.25950/2c59c9d6
Computes grain boundary energy for a range of tilt angles given a crystal structure, tilt axis, and material.
Equilibrium lattice constant and cohesive energy of a cubic lattice at zero temperature and pressure v007
Creators: Daniel S. Karls and Junhao Li
Contributor: karls
Publication Year: 2019
DOI: https://doi.org/10.25950/2765e3bf
Equilibrium lattice constant and cohesive energy of a cubic lattice at zero temperature and pressure.
Creators: Daniel S. Karls and Junhao Li
Contributor: karls
Publication Year: 2019
DOI: https://doi.org/10.25950/2765e3bf
Equilibrium lattice constant and cohesive energy of a cubic lattice at zero temperature and pressure.
Equilibrium lattice constants for hexagonal bulk structures at zero temperature and pressure v005
Creators: Daniel S. Karls and Junhao Li
Contributor: karls
Publication Year: 2019
DOI: https://doi.org/10.25950/c339ca32
Calculates lattice constant of hexagonal bulk structures at zero temperature and pressure by using simplex minimization to minimize the potential energy.
Creators: Daniel S. Karls and Junhao Li
Contributor: karls
Publication Year: 2019
DOI: https://doi.org/10.25950/c339ca32
Calculates lattice constant of hexagonal bulk structures at zero temperature and pressure by using simplex minimization to minimize the potential energy.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Equilibrium lattice constants for hcp Al v005 | view | 128671 | |
| Equilibrium lattice constants for hcp Co v005 | view | 148566 | |
| Equilibrium lattice constants for hcp Cr v005 | view | 148492 | |
| Equilibrium lattice constants for hcp Fe v005 | view | 157883 | |
| Equilibrium lattice constants for hcp Ni v005 | view | 154045 |
Linear thermal expansion coefficient of cubic crystal structures v002
Creators:
Contributor: mjwen
Publication Year: 2024
DOI: https://doi.org/10.25950/9d9822ec
This Test Driver uses LAMMPS to compute the linear thermal expansion coefficient at a finite temperature under a given pressure for a cubic lattice (fcc, bcc, sc, diamond) of a single given species.
Creators:
Contributor: mjwen
Publication Year: 2024
DOI: https://doi.org/10.25950/9d9822ec
This Test Driver uses LAMMPS to compute the linear thermal expansion coefficient at a finite temperature under a given pressure for a cubic lattice (fcc, bcc, sc, diamond) of a single given species.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Linear thermal expansion coefficient of bcc Cr at 293.15 K under a pressure of 0 MPa v002 | view | 501282 | |
| Linear thermal expansion coefficient of bcc Fe at 293.15 K under a pressure of 0 MPa v002 | view | 594927 | |
| Linear thermal expansion coefficient of fcc Al at 293.15 K under a pressure of 0 MPa v002 | view | 563639 | |
| Linear thermal expansion coefficient of fcc Ni at 293.15 K under a pressure of 0 MPa v002 | view | 702203 |
Phonon dispersion relations for an fcc lattice v004
Creators: Matt Bierbaum
Contributor: mattbierbaum
Publication Year: 2019
DOI: https://doi.org/10.25950/64f4999b
Calculates the phonon dispersion relations for fcc lattices and records the results as curves.
Creators: Matt Bierbaum
Contributor: mattbierbaum
Publication Year: 2019
DOI: https://doi.org/10.25950/64f4999b
Calculates the phonon dispersion relations for fcc lattices and records the results as curves.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Phonon dispersion relations for fcc Al v004 | view | 124934 | |
| Phonon dispersion relations for fcc Ni v004 | view | 134578 |
Stacking and twinning fault energies of an fcc lattice at zero temperature and pressure v002
Creators:
Contributor: SubrahmanyamPattamatta
Publication Year: 2019
DOI: https://doi.org/10.25950/b4cfaf9a
Intrinsic and extrinsic stacking fault energies, unstable stacking fault energy, unstable twinning energy, stacking fault energy as a function of fractional displacement, and gamma surface for a monoatomic FCC lattice at zero temperature and pressure.
Creators:
Contributor: SubrahmanyamPattamatta
Publication Year: 2019
DOI: https://doi.org/10.25950/b4cfaf9a
Intrinsic and extrinsic stacking fault energies, unstable stacking fault energy, unstable twinning energy, stacking fault energy as a function of fractional displacement, and gamma surface for a monoatomic FCC lattice at zero temperature and pressure.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Stacking and twinning fault energies for fcc Al v002 | view | 19088929 | |
| Stacking and twinning fault energies for fcc Ni v002 | view | 12687356 |
High-symmetry surface energies in cubic lattices and broken bond model v004
Creators: Matt Bierbaum
Contributor: mattbierbaum
Publication Year: 2019
DOI: https://doi.org/10.25950/6c43a4e6
Calculates the surface energy of several high symmetry surfaces and produces a broken-bond model fit. In latex form, the fit equations are given by:
E_{FCC} (\vec{n}) = p_1 (4 \left( |x+y| + |x-y| + |x+z| + |x-z| + |z+y| +|z-y|\right)) + p_2 (8 \left( |x| + |y| + |z|\right)) + p_3 (2 ( |x+ 2y + z| + |x+2y-z| + |x-2y + z| + |x-2y-z| + |2x+y+z| + |2x+y-z| +|2x-y+z| +|2x-y-z| +|x+y+2z| +|x+y-2z| +|x-y+2z| +|x-y-2z| ) + c
E_{BCC} (\vec{n}) = p_1 (6 \left( | x+y+z| + |x+y-z| + |-x+y-z| + |x-y+z| \right)) + p_2 (8 \left( |x| + |y| + |z|\right)) + p_3 (4 \left( |x+y| + |x-y| + |x+z| + |x-z| + |z+y| +|z-y|\right)) +c.
In Python, these two fits take the following form:
def BrokenBondFCC(params, index):
import numpy
x, y, z = index
x = x / numpy.sqrt(x**2.+y**2.+z**2.)
y = y / numpy.sqrt(x**2.+y**2.+z**2.)
z = z / numpy.sqrt(x**2.+y**2.+z**2.)
return params[0]*4* (abs(x+y) + abs(x-y) + abs(x+z) + abs(x-z) + abs(z+y) + abs(z-y)) + params[1]*8*(abs(x) + abs(y) + abs(z)) + params[2]*(abs(x+2*y+z) + abs(x+2*y-z) +abs(x-2*y+z) +abs(x-2*y-z) + abs(2*x+y+z) +abs(2*x+y-z) +abs(2*x-y+z) +abs(2*x-y-z) + abs(x+y+2*z) +abs(x+y-2*z) +abs(x-y+2*z) +abs(x-y-2*z))+params[3]
def BrokenBondBCC(params, x, y, z):
import numpy
x, y, z = index
x = x / numpy.sqrt(x**2.+y**2.+z**2.)
y = y / numpy.sqrt(x**2.+y**2.+z**2.)
z = z / numpy.sqrt(x**2.+y**2.+z**2.)
return params[0]*6*(abs(x+y+z) + abs(x-y-z) + abs(x-y+z) + abs(x+y-z)) + params[1]*8*(abs(x) + abs(y) + abs(z)) + params[2]*4* (abs(x+y) + abs(x-y) + abs(x+z) + abs(x-z) + abs(z+y) + abs(z-y)) + params[3]
Creators: Matt Bierbaum
Contributor: mattbierbaum
Publication Year: 2019
DOI: https://doi.org/10.25950/6c43a4e6
Calculates the surface energy of several high symmetry surfaces and produces a broken-bond model fit. In latex form, the fit equations are given by:
E_{FCC} (\vec{n}) = p_1 (4 \left( |x+y| + |x-y| + |x+z| + |x-z| + |z+y| +|z-y|\right)) + p_2 (8 \left( |x| + |y| + |z|\right)) + p_3 (2 ( |x+ 2y + z| + |x+2y-z| + |x-2y + z| + |x-2y-z| + |2x+y+z| + |2x+y-z| +|2x-y+z| +|2x-y-z| +|x+y+2z| +|x+y-2z| +|x-y+2z| +|x-y-2z| ) + c
E_{BCC} (\vec{n}) = p_1 (6 \left( | x+y+z| + |x+y-z| + |-x+y-z| + |x-y+z| \right)) + p_2 (8 \left( |x| + |y| + |z|\right)) + p_3 (4 \left( |x+y| + |x-y| + |x+z| + |x-z| + |z+y| +|z-y|\right)) +c.
In Python, these two fits take the following form:
def BrokenBondFCC(params, index):
import numpy
x, y, z = index
x = x / numpy.sqrt(x**2.+y**2.+z**2.)
y = y / numpy.sqrt(x**2.+y**2.+z**2.)
z = z / numpy.sqrt(x**2.+y**2.+z**2.)
return params[0]*4* (abs(x+y) + abs(x-y) + abs(x+z) + abs(x-z) + abs(z+y) + abs(z-y)) + params[1]*8*(abs(x) + abs(y) + abs(z)) + params[2]*(abs(x+2*y+z) + abs(x+2*y-z) +abs(x-2*y+z) +abs(x-2*y-z) + abs(2*x+y+z) +abs(2*x+y-z) +abs(2*x-y+z) +abs(2*x-y-z) + abs(x+y+2*z) +abs(x+y-2*z) +abs(x-y+2*z) +abs(x-y-2*z))+params[3]
def BrokenBondBCC(params, x, y, z):
import numpy
x, y, z = index
x = x / numpy.sqrt(x**2.+y**2.+z**2.)
y = y / numpy.sqrt(x**2.+y**2.+z**2.)
z = z / numpy.sqrt(x**2.+y**2.+z**2.)
return params[0]*6*(abs(x+y+z) + abs(x-y-z) + abs(x-y+z) + abs(x+y-z)) + params[1]*8*(abs(x) + abs(y) + abs(z)) + params[2]*4* (abs(x+y) + abs(x-y) + abs(x+z) + abs(x-z) + abs(z+y) + abs(z-y)) + params[3]
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Broken-bond fit of high-symmetry surface energies in bcc Cr v004 | view | 161434 | |
| Broken-bond fit of high-symmetry surface energies in bcc Fe v004 | view | 159912 | |
| Broken-bond fit of high-symmetry surface energies in fcc Al v004 | view | 174443 | |
| Broken-bond fit of high-symmetry surface energies in fcc Ni v004 | view | 110600 |
Monovacancy formation energy and relaxation volume for cubic and hcp monoatomic crystals v001
Creators:
Contributor: efuem
Publication Year: 2023
DOI: https://doi.org/10.25950/fca89cea
Computes the monovacancy formation energy and relaxation volume for cubic and hcp monoatomic crystals.
Creators:
Contributor: efuem
Publication Year: 2023
DOI: https://doi.org/10.25950/fca89cea
Computes the monovacancy formation energy and relaxation volume for cubic and hcp monoatomic crystals.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Monovacancy formation energy and relaxation volume for bcc Cr | view | 460938 | |
| Monovacancy formation energy and relaxation volume for bcc Fe | view | 1513858 | |
| Monovacancy formation energy and relaxation volume for fcc Al | view | 327611 | |
| Monovacancy formation energy and relaxation volume for fcc Ni | view | 351685 | |
| Monovacancy formation energy and relaxation volume for hcp Co | view | 382017 |
Vacancy formation and migration energies for cubic and hcp monoatomic crystals v001
Creators:
Contributor: efuem
Publication Year: 2023
DOI: https://doi.org/10.25950/c27ba3cd
Computes the monovacancy formation and migration energies for cubic and hcp monoatomic crystals.
Creators:
Contributor: efuem
Publication Year: 2023
DOI: https://doi.org/10.25950/c27ba3cd
Computes the monovacancy formation and migration energies for cubic and hcp monoatomic crystals.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Vacancy formation and migration energy for bcc Cr | view | 4178479 | |
| Vacancy formation and migration energy for bcc Fe | view | 3844094 | |
| Vacancy formation and migration energy for fcc Al | view | 2017570 | |
| Vacancy formation and migration energy for fcc Ni | view | 1770573 | |
| Vacancy formation and migration energy for hcp Co | view | 4410457 |
ElasticConstantsCubic__TD_011862047401_006
ElasticConstantsHexagonal__TD_612503193866_004
EquilibriumCrystalStructure__TD_457028483760_000
EquilibriumCrystalStructure__TD_457028483760_002
GrainBoundaryCubicCrystalSymmetricTiltRelaxedEnergyVsAngle__TD_410381120771_003
PhononDispersionCurve__TD_530195868545_004
SurfaceEnergyCubicCrystalBrokenBondFit__TD_955413365818_004
No Driver
| Test | Error Categories | Link to Error page |
|---|---|---|
| Elastic constants for diamond Al at zero temperature v001 | other | view |
| Elastic constants for diamond Co at zero temperature v001 | other | view |
| Elastic constants for diamond Cr at zero temperature v001 | other | view |
| Elastic constants for diamond Fe at zero temperature v001 | other | view |
| Elastic constants for diamond Ni at zero temperature v001 | other | view |
ElasticConstantsHexagonal__TD_612503193866_004
| Test | Error Categories | Link to Error page |
|---|---|---|
| Elastic constants for hcp Al at zero temperature v004 | other | view |
| Elastic constants for hcp Co at zero temperature v004 | other | view |
| Elastic constants for hcp Cr at zero temperature v004 | other | view |
| Elastic constants for hcp Fe at zero temperature v004 | other | view |
| Elastic constants for hcp Ni at zero temperature v004 | other | view |
EquilibriumCrystalStructure__TD_457028483760_000
| Test | Error Categories | Link to Error page |
|---|---|---|
| Equilibrium crystal structure and energy for AlNi in AFLOW crystal prototype A4B3_cI112_230_af_g v000 | other | view |
| Equilibrium crystal structure and energy for Co in AFLOW crystal prototype A_tP28_136_f2ij v000 | other | view |
EquilibriumCrystalStructure__TD_457028483760_002
GrainBoundaryCubicCrystalSymmetricTiltRelaxedEnergyVsAngle__TD_410381120771_003
PhononDispersionCurve__TD_530195868545_004
| Test | Error Categories | Link to Error page |
|---|---|---|
| Phonon dispersion relations for fcc Al v004 | other | view |
| Phonon dispersion relations for fcc Ni v004 | other | view |
SurfaceEnergyCubicCrystalBrokenBondFit__TD_955413365818_004
| Test | Error Categories | Link to Error page |
|---|---|---|
| Broken-bond fit of high-symmetry surface energies in bcc Cr v004 | other | view |
| Broken-bond fit of high-symmetry surface energies in bcc Fe v004 | other | view |
| Broken-bond fit of high-symmetry surface energies in fcc Al v004 | other | view |
| Broken-bond fit of high-symmetry surface energies in fcc Ni v004 | other | view |
No Driver
| Verification Check | Error Categories | Link to Error page |
|---|---|---|
| MemoryLeak__VC_561022993723_004 | other | view |
| PeriodicitySupport__VC_895061507745_004 | other | view |
| EAM_Dynamo_FarkasCaro_2020_FeNiCrCoAl__MO_820335782779_000.txz | Tar+XZ | Linux and OS X archive |
| EAM_Dynamo_FarkasCaro_2020_FeNiCrCoAl__MO_820335782779_000.zip | Zip | Windows archive |
This Model requires a Model Driver. Archives for the Model Driver EAM_Dynamo__MD_120291908751_005 appear below.
| EAM_Dynamo__MD_120291908751_005.txz | Tar+XZ | Linux and OS X archive |
| EAM_Dynamo__MD_120291908751_005.zip | Zip | Windows archive |