Citations
This panel presents information regarding the papers that have cited the interatomic potential (IP) whose page you are on.
The OpenKIM machine learning based Deep Citation framework is used to determine whether the citing article actually used the IP in computations (denoted by "USED") or only provides it as a background citation (denoted by "NOT USED"). For more details on Deep Citation and how to work with this panel, click the documentation link at the top of the panel.
The word cloud to the right is generated from the abstracts of IP principle source(s) (given below in "How to Cite") and the citing articles that were determined to have used the IP in order to provide users with a quick sense of the types of physical phenomena to which this IP is applied.
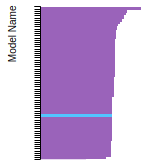
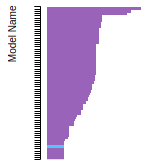
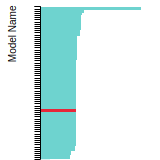
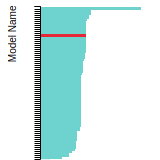
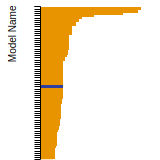
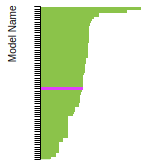
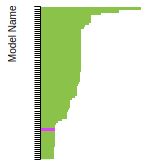
The bar chart shows the number of articles that cited the IP per year. Each bar is divided into green (articles that USED the IP) and blue (articles that did NOT USE the IP).
Users are encouraged to correct Deep Citation errors in determination by clicking the speech icon next to a citing article and providing updated information. This will be integrated into the next Deep Citation learning cycle, which occurs on a regular basis.
OpenKIM acknowledges the support of the Allen Institute for AI through the Semantic Scholar project for providing citation information and full text of articles when available, which are used to train the Deep Citation ML algorithm.
|
This panel provides information on past usage of this interatomic potential (IP) powered by the OpenKIM Deep Citation framework. The word cloud indicates typical applications of the potential. The bar chart shows citations per year of this IP (bars are divided into articles that used the IP (green) and those that did not (blue)). The complete list of articles that cited this IP is provided below along with the Deep Citation determination on usage. See the Deep Citation documentation for more information.
Help us to determine which of the papers that cite this potential actually used it to perform calculations. If you know, click the .
USED (definite) M. Munaji, G. A. Buntoro, A. Purniawan, and R. Arifin, “Molecular Dynamics Simulations of Iron-Joining Using Copper as a Filler Metal,” Makara Journal of Science. 2018. link Times cited: 2 Abstract: The study of the liquid filler metal infiltration on the nar… read moreAbstract: The study of the liquid filler metal infiltration on the narrow channel of adjoining metal bears importance in understanding the mechanism of the metal brazing process. In this study, we employed the molecular dynamics simulation to understand the mechanism of Cu liquid infiltration through the narrow channel of Fe slabs. Our simulation showed that the wetting process of Fe surfaces by Cu liquid precedes the infiltration process. This study also revealed that the channel became narrower and blockages were found in the channel due to the deformation of Fe surface. In addition to the effect of viscous drag, this process should also contribute to the decreasing speed of the Cu liquid front. read less USED (definite) Y. Cheng, W. Cui, L. Wang, C. Peng, S. Wang, and Y.-yang Wang, “Vitrification and Crystallization of Phase-Separated Metallic Liquid.” 2017. link Times cited: 5 Abstract: The liquid–liquid phase separation (LLPS) behavior of Fe50Cu… read moreAbstract: The liquid–liquid phase separation (LLPS) behavior of Fe50Cu50 melt from 3500 K to 300 K with different rapid quenching is investigated by molecular dynamics (MD) simulation based on the embedded atom method (EAM). The liquid undergoes metastable phase separation by spinodal decomposition in the undercooled regime and subsequently solidifies into three different Fe-rich microstructures: the interconnected-type structure is kept in the glass and crystal at a higher cooling rate, while the Fe-rich droplets are found to crystalize at a lower cooling rate. During the crystallization process, only Fe-rich clusters can act as the solid nuclei. The twinning planes can be observed in the crystal and only the homogeneous atomic stacking shows mirror symmetry along the twinning boundary. Our present work provides atomic-scale understanding of LLPS melt during the cooling process. read less USED (definite) S. Shao and J. Wang, “Relaxation Mechanisms, Structure and Properties of Semi-Coherent Interfaces.” 2015. link Times cited: 10 Abstract: In this work, using the Cu–Ni (111) semi-coherent interface … read moreAbstract: In this work, using the Cu–Ni (111) semi-coherent interface as a model system, we combine atomistic simulations and defect theory to reveal the relaxation mechanisms, structure, and properties of semi-coherent interfaces. By calculating the generalized stacking fault energy (GSFE) profile of the interface, two stable structures and a high-energy structure are located. During the relaxation, the regions that possess the stable structures expand and develop into coherent regions; the regions with high-energy structure shrink into the intersection of misfit dislocations (nodes). This process reduces the interface excess potential energy but increases the core energy of the misfit dislocations and nodes. The core width is dependent on the GSFE of the interface. The high-energy structure relaxes by relative rotation and dilatation between the crystals. The relative rotation is responsible for the spiral pattern at nodes. The relative dilatation is responsible for the creation of free volume at nodes, which facilitates the nodes’ structural transformation. Several node structures have been observed and analyzed. The various structures have significant impact on the plastic deformation in terms of lattice dislocation nucleation, as well as the point defect formation energies. read less USED (high confidence) B. Waters, D. S. Karls, I. Nikiforov, R. Elliott, E. Tadmor, and B. Runnels, “Automated determination of grain boundary energy and potential-dependence using the OpenKIM framework,” Computational Materials Science. 2022. link Times cited: 5 USED (high confidence) W. Guo, C. Wu, X. Meng, C. Luo, and Z. Lin, “Molecular dynamics simulation-based microstructure evolution and subsurface damage of Fe-Ni alloy grinding,” Journal of Intelligent Manufacturing and Special Equipment. 2022. link Times cited: 0 Abstract: PurposeMolecular dynamics is an emerging simulation techniqu… read moreAbstract: PurposeMolecular dynamics is an emerging simulation technique in the field of machining in recent years. Many researchers have tried to simulate different processing methods of various materials with the theory of molecular dynamics (MD), and some preliminary conclusions have been obtained. However, the application of MD simulation is more limited compared with traditional finite element model (FEM) simulation technique due to the complex modeling approach and long computation time. Therefore, more studies on the MD simulations are required to provide a reliable theoretical basis for the nanoscale interpretation of grinding process. This study investigates the crystal structures, dislocations, force, temperature and subsurface damage (SSD) in the grinding of iron-nickel alloy using MD analysis.Design/methodology/approach In this study the simulation model is established on the basis of the workpiece and single cubic boron nitride (CBN) grit with embedded atom method and Morse potentials describing the forces and energies between different atoms. The effects of grinding parameters on the material microstructure are studied based on the simulation results.FindingsWhen CBN grit goes through one of the grains, the arrangement of atoms within the grain will be disordered, but other grains will not be easily deformed due to the protection of the grain boundaries. Higher grinding speed and larger cutting depth can cause greater impact of grit on the atoms, and more body-centered cubic (BCC) structures will be destroyed. The dislocations will appear in grain boundaries due to the rearrangement of atoms in grinding. The increase of grinding speed results in the more transformation from BCC to amorphous structures.Originality/valueThis study is aimed to study the grinding of Fe-Ni alloy (maraging steel) with single grit through MD simulation method, and to reveal the microstructure evolution within the affected range of SSD layer in the workpiece. The simulation model of polycrystalline structure of Fe-Ni maraging steel and grinding process of single CBN grit is constructed based on the Voronoi algorithm. The atomic accumulation, transformation of crystal structures, evolution of dislocations as well as the generation of SSD are discussed according to the simulation results. read less USED (high confidence) M. Fokt, G. Adjanor, and T. Jourdan, “A variable-gap model for helium bubbles in nickel,” Computational Materials Science. 2022. link Times cited: 1 USED (high confidence) S. Mori, N. Matsuda, T. Okita, M. Aichi, M. Itakura, and K. Suzuki, “Modeling Changes in the Second Harmonic Generation of Ultrasonic Waves Having Wavelengths Beyond the Length Scale of Conventional Molecular Dynamics,” MatSciRN: Other Electronic. 2022. link Times cited: 3 Abstract: The nonlinear ultrasonic (NLU) technique is attracting atten… read moreAbstract: The nonlinear ultrasonic (NLU) technique is attracting attention as a nondestructive method for the detection of nanostructures in crystalline materials. In this study, we developed a method to quantify the changes in NLU signals associated with nanostructures formation using molecular dynamics (MD) simulations. To achieve this, we used a nonreflective boundary, which reduces the computational cost to the first power of the wavelength; this is distinct from previous proposals using conventional MD method, for which the computational cost is proportional to the square of the wavelength. The nonreflective boundary eliminates the influence of reflected waves at the detection position by setting a buffer region at the end of the simulated cell opposite from the wave source, and the displacements and velocities of all atoms in this region are periodically reset. Using this method, we succeeded in speeding up the calculation by up to 4000 times while maintaining similar accuracy to that of the conventional MD method. Thus, it is possible to extend the NLU wavelength by approximately four orders of magnitude, which approaches the wavelengths used in actual inspections and, thus, simulate the changes in the NLU signals induced by nanostructures by MD. Consequently, this method will contribute to the development of a robust inspection technique based on scientific principles. read less USED (high confidence) L. Xu, L. Casillas-Trujillo, Y. Gao, and H. Xu, “Compositional effects on stacking fault energies in Ni-based alloys using first-principles and atomistic simulations,” Computational Materials Science. 2021. link Times cited: 5 USED (high confidence) H. Zhang, Y.-li Chen, X. Wang, H. Li, and Y. Li, “Molecular Dynamics Research on the Impact of Vacancies on Cu Precipitation in BCC-Fe,” Materials. 2021. link Times cited: 0 Abstract: The molecular dynamics (MD) simulation method was used to ex… read moreAbstract: The molecular dynamics (MD) simulation method was used to explore the impact of vacancy concentration (0 at%, 0.1 at% and 0.2 at%) on the diffusion and precipitation rate of Cu atoms in the Fe-3.5Cu alloy and the growth of Cu precipitation during the aging process of the alloy. The mechanism of the influence of Cu precipitation relative to the tensile properties of Fe-3.5Cu alloy was investigated. The results showed that the presence of vacancies will promote the diffusion and precipitation of Cu atoms in the Fe-3.5Cu alloy, but the diffusion and precipitation rate of Cu atoms does not always increase with the increase in vacancies. In the alloy containing 0.2 at% vacancies, the diffusion and precipitation rate of Cu atoms is lower than that in the alloy containing 0.1 at% vacancies. During the aging process, when the alloy contains no vacancies, no Cu precipitates will be produced. In the alloy containing 0.1 at% vacancies, the size of the Cu precipitates produced is larger than the size of the Cu precipitates produced in the alloy containing 0.2 at% vacancies, but the number of precipitates is less than that in the alloy with 0.2 at% vacancies. During the tensile process, the Cu precipitates will promote early occurrence of phase transition of the internal crystal structure in the Fe-3.5Cu alloy system, and lead to the generation of vacancy defects in the system, thus weakening the yield strength and strain hardening strength of the alloy. read less USED (high confidence) S. Dong, X.-Y. Liu, and C. Zhou, “Atomistic modeling of plastic deformation in B2-FeAl/Al nanolayered composites,” Journal of Materials Science. 2021. link Times cited: 0 USED (high confidence) S. Eder, P. Grützmacher, M. R. Ripoll, and J. Belak, “Elucidating the Onset of Plasticity in Sliding Contacts Using Differential Computational Orientation Tomography,” Tribology Letters. 2021. link Times cited: 9 USED (high confidence) X. Xu, P. Binkele, W. Verestek, and S. Schmauder, “Molecular Dynamics Simulation of High-Temperature Creep Behavior of Nickel Polycrystalline Nanopillars,” Molecules. 2021. link Times cited: 0 Abstract: As Nickel (Ni) is the base of important Ni-based superalloys… read moreAbstract: As Nickel (Ni) is the base of important Ni-based superalloys for high-temperature applications, it is important to determine the creep behavior of its nano-polycrystals. The nano-tensile properties and creep behavior of nickel polycrystalline nanopillars are investigated employing molecular dynamics simulations under different temperatures, stresses, and grain sizes. The mechanisms behind the creep behavior are analyzed in detail by calculating the stress exponents, grain boundary exponents, and activation energies. The novel results in this work are summarized in a deformation mechanism map and are in good agreement with Ashby’s experimental results for pure Ni. Through the deformation diagram, dislocation creep dominates the creep process when applying a high stress, while grain boundary sliding prevails at lower stress levels. These two mechanisms could also be coupled together for a low-stress but a high-temperature creep simulation. In this work, the dislocation creep is clearly observed and discussed in detail. Through analyzing the activation energies, vacancy diffusion begins to play an important role in enhancing the grain boundary creep in the creep process when the temperature is above 1000 K. read less USED (high confidence) K. Kanamori, S. Toriumi, Y. Kimoto, and A. Yonezu, “Repeated Laser Shock-Wave Adhesion Test for Metallic Coatings: Adhesion Durability and Its Mechanism Studied by Molecular Dynamics Simulation,” Coatings. 2021. link Times cited: 2 Abstract: We evaluated the adhesion of polycrystalline metallic coatin… read moreAbstract: We evaluated the adhesion of polycrystalline metallic coatings using the laser shock-wave adhesion test (LaSAT). This study used Cu plating on stainless steel as a coating model. The adhesion strength and toughness were successfully estimated using LaSAT and finite element method with cohesive zone model. Next, repeated LaSAT was conducted to apply cyclic loading to evaluate adhesion fatigue life, i.e., the number of loading cycles required for delamination. Furthermore, this study performed molecular dynamics (MD) simulations to elucidate the adhesion mechanism for the Cu/Fe interface. To verify our model, the interfacial fracture toughness was computed using the MD simulation and compared with the results of LaSAT. Next, cyclic loading was applied to the MD model to investigate crack initiation around the interface. We found that dislocations are generated from the internal grain and are accumulated at grain boundaries. This accumulation results in fatigue crack initiation due to stress concentration. read less USED (high confidence) K. Chen et al., “Molecular Dynamics Simulations of High-speed Nanoscale Sliding with Third Medium,” IOP Conference Series: Earth and Environmental Science. 2021. link Times cited: 0 Abstract: 3D non-equilibrium molecular dynamics simulations are perfor… read moreAbstract: 3D non-equilibrium molecular dynamics simulations are performed to investigate the friction characteristic of Fe-Fe tribopair system under third medium condition. A Fe-Fe sliding simulation model with the soft third medium (Cu nanoparticle) is built. The Friction force, evolution of the structure of interface and the temperature profiles of the sliding system are obtained. The influence of the sliding velocity to the temperature and structure change under third medium is investigated. The influence of Cu nanoparticle to the microstructure evolution and change of the friction characteristic is extremely concerned. The results show that the Cu nanoparticle can decrease the friction force and average temperature under the relatively low velocity (25m/s). However, under high velocity (150m/s), the positive effect is not obvious. A Cu nano-film would form on the surface, which is useful for weakening the destruction of the interface, and protecting the sliding blocks. Under high velocity, a mixing layer would be formed in both two cases (with or without Cu nanoparticle). read less USED (high confidence) W. Nöhring, J.-C. Griesser, P. Dondl, and L. Pastewka, “Surface lattice Green’s functions for high-entropy alloys,” Modelling and Simulation in Materials Science and Engineering. 2021. link Times cited: 0 Abstract: We study the surface elastic response of pure Ni, the random… read moreAbstract: We study the surface elastic response of pure Ni, the random alloy FeNiCr and an average FeNiCr alloy in terms of the surface lattice Green’s function. We propose a scheme for computing per-site Green’s function and study their per-site variations. The average FeNiCr alloys accurately reproduces the mean Green’s function of the full random alloy. Variation around this mean is largest near the edge of the surface Brillouin-zone and decays as q −2 with wavevector q towards the Γ-point. We also present expressions for the continuum surface Green’s function of anisotropic solids of finite and infinite thickness and show that the atomistic Green’s function approaches continuum near the Γ-point. Our results are a first step towards efficient contact calculations and Peierls–Nabarro type models for dislocations in high-entropy alloys. read less USED (high confidence) H. Zhang, X. Wang, L. Huirong, C. Li, and L. Yungang, “Molecular Dynamics Study on the Impact of Cu Clusters at the BCC-Fe Grain Boundary on the Tensile Properties of Crystal,” Metals. 2020. link Times cited: 3 Abstract: The molecular dynamics (MD) method was used to simulate and … read moreAbstract: The molecular dynamics (MD) method was used to simulate and calculate the segregation energy and cohesive energy of Cu atoms at the Σ3{111}(110) and Σ3{112}(110) grain boundaries, and the tensile properties of the BCC-Fe crystal, with the grain boundaries containing coherent Cu clusters of different sizes (a diameter of 10 Å, 15 Å and 20 Å). The results showed that Cu atoms will spontaneously segregate towards the grain boundaries and tend to exist in the form of large-sized, low-density Cu clusters at the grain boundaries. When Cu cluster exists at the Σ3{111}(110) grain boundary, the increase in the size of the Cu cluster leads to an increase in the probability of vacancy formation inside the Cu cluster during the tensile process, weakening the breaking strength of the crystal. When the Cu cluster exists at the Σ3{112}(110) grain boundary, the Cu cluster with a diameter of 10 Å will reduce the strain hardening strength of the crystal, but the plastic deformation ability of the crystal will not be affected, and the existence of Cu clusters with a diameter of 15 Å and 20 Å will suppress the structural phase transformation of the crystal, and significantly decrease the plastic deformation ability of the crystal, thereby resulting in embrittlement of the crystal. read less USED (high confidence) J. Chen, P. Li, and E. E. Lin, “A molecular dynamics study on the mechanical properties of Fe–Ni alloy nanowires and their temperature dependence,” RSC Advances. 2020. link Times cited: 7 Abstract: Fe–Ni alloy nanowires are widely used in high-density magnet… read moreAbstract: Fe–Ni alloy nanowires are widely used in high-density magnetic memories and catalysts due to their unique magnetic and electrochemical properties. Understanding the deformation mechanism and mechanical property of Fe–Ni alloy nanowires is of great importance for the development of devices. However, the detailed deformation mechanism of the alloy nanowires at different temperatures is unclear. Herein, the deformation mechanism of Fe–Ni alloy nanowires and their mechanical properties were investigated via the molecular dynamics simulation method. It was found that the local atomic pressure fluctuation of the Fe–Ni alloy nanowire surface became more prominent with an increase in the Ni content. At low temperature conditions (<50 K), the plastic deformation mechanism of the Fe–Ni alloy nanowires switched from the twinning mechanism to the dislocation slip mechanism with the increase in the Ni content from 0.5 at% to 8.0 at%. In the temperature range of 50–800 K, the dislocation slip mechanism dominated the deformation. Simulation results indicated that there was a significant linear relationship between the Ni content, temperature, and ultimate stress in the temperature range of 50–800 K. Our research revealed the association between the deformation mechanism and temperature in Fe–Ni alloy nanowires, which may facilitate new alloy nanowire designs. read less USED (high confidence) M. Wang, G. Zhang, H. Xu, and Y. Zhang, “Atomistic Simulations and Experimental Investigations of the Diffusion Behavior of Steel/ZCuPb20Sn5 Bimetals,” THE Coatings. 2020. link Times cited: 3 Abstract: A hybrid verification method consisting of experiments and m… read moreAbstract: A hybrid verification method consisting of experiments and molecular dynamics simulations was implemented to investigate the diffusion behaviour of steel/ZCuPb20Sn5 bimetals. The effects of different carbon steels (Q235 steel, 45 steel, and T8 steel), pouring temperatures, and holding times on their microstructures and mechanical properties were studied to obtain the optimum process parameters. The experimental results indicated that the pouring temperature and holding time played an imperative role in improving the shear strength of the steel/copper bimetallic composite. The highest bonding strength of all the steel/copper bimetallic composites was obtained at 1523 K and the holding time of 40 min. Moreover, the carbon steel of 45 steel with a ZCuPb20Sn5 interface exhibited the highest bonding strength because of the appropriate pearlite content along with the preferable structure and micro-hardness for the considered diffusion width and bonding strength. Meanwhile, the diffusion distance of copper atoms in the carbon steel matrix was smaller than that of iron atoms in the ZCuPb20Sn5 matrix. In the simulation results, the diffusion coefficient of Cu atoms was smaller than that of Fe atoms, but the diffusion distance of Fe atoms in the Cu bulk was larger than that of Cu atoms in the Fe bulk; this showed a significant agreement with the experimental result. read less USED (high confidence) L.-F. Zhu, F. Körmann, A. Ruban, J. Neugebauer, and B. Grabowski, “Performance of the standard exchange-correlation functionals in predicting melting properties fully from first principles: Application to Al and magnetic Ni,” Physical Review B. 2020. link Times cited: 10 Abstract: We apply the efficient two-optimized references thermodynami… read moreAbstract: We apply the efficient two-optimized references thermodynamic integration using Langevin dynamics method [Phys. Rev. B 96, 224202 (2017)2469-995010.1103/PhysRevB.96.224202] to calculate highly accurate melting properties of Al and magnetic Ni from first principles. For Ni we carefully investigate the impact of magnetism on the liquid and solid free energies including longitudinal spin fluctuations and the reverse influence of atomic vibrations on magnetic properties. We show that magnetic fluctuations are effectively canceling out for both phases and are thus not altering the predicted melting temperature. For both elements, the generalized gradient approximation (GGA) and the local-density approximation (LDA) are used for the exchange-correlation functional revealing a reliable ab initio confidence interval capturing the respective experimental melting point, enthalpy of fusion, and entropy of fusion. read less USED (high confidence) R. Khusnutdinoff, R. Khairullina, A. Beltyukov, V. Lad’yanov, and A. Mokshin, “Viscous properties of nickel-containing binary metal melts,” Journal of Physics: Condensed Matter. 2020. link Times cited: 0 Abstract: The paper presents the results of molecular dynamics study o… read moreAbstract: The paper presents the results of molecular dynamics study of the viscosity of nickel-containing binary metal melts for a wide range of temperatures, including the region of the equilibrium liquid phase and supercooled melt. It is shown that the temperature dependencies of the viscosity of binary metal melts are described by the Kelton’s quasi-universal model. Based on the analysis of the viscosity coefficient of the binary melt composition within the framework of the Rosenfeld’s scale transformations, it has been established that to correctly describe the viscosity of binary/multicomponent metal melts within the framework of entropy models, it is necessary to use a more complex representation of the excess entropy S ex than in the approximation of pair correlation entropy S 2. read less USED (high confidence) O. Filatov and O. Soldatenko, “Influence of Glide Dislocation Motion on Self-Diffusion in b.c.c. Fe. A Molecular Dynamics Study,” Metallofizika I Noveishie Tekhnologii. 2020. link Times cited: 1 Abstract: The interaction of glide dislocations with own interstitial … read moreAbstract: The interaction of glide dislocations with own interstitial atoms in α-Fe is studied. As a method of investigation the molecular dynamics simulation is used. The modelled sample is deformed with a rate close to the deformation rates under pulsed laser treatment. Mass transfer parameter for b.c.c. Fe under laser pulse irradiation is calculated. As established, the core of moving dislocation is a trap for interstitial atom. The influence of temperature and deformation rate on mass-transfer coefficient is studied. read less USED (high confidence) A. Tsukanov et al., “Effect of Cold-Sintering Parameters on Structure, Density, and Topology of Fe–Cu Nanocomposites,” Materials. 2020. link Times cited: 8 Abstract: The design of advanced nanostructured materials with predete… read moreAbstract: The design of advanced nanostructured materials with predetermined physical properties requires knowledge of the relationship between these properties and the internal structure of the material at the nanoscale, as well as the dependence of the internal structure on the production (synthesis) parameters. This work is the first report of computer-aided analysis of high pressure consolidation (cold sintering) of bimetallic nanoparticles of two immiscible (Fe and Cu) metals using the embedded atom method (EAM). A detailed study of the effect of cold sintering parameters on the internal structure and properties of bulk Fe–Cu nanocomposites was conducted within the limitations of the numerical model. The variation of estimated density and bulk porosity as a function of Fe-to-Cu ratio and consolidation pressure was found in good agreement with the experimental data. For the first time, topological analysis using Minkowski functionals was applied to characterize the internal structure of a bimetallic nanocomposite. The dependence of topological invariants on input processing parameters was described for various components and structural phases. The model presented allows formalizing the relationship between the internal structure and properties of the studied nanocomposites. Based on the obtained topological invariants and Hadwiger’s theorem we propose a new tool for computer-aided design of bimetallic Fe–Cu nanocomposites. read less USED (high confidence) J. Sublet et al., “Neutron-induced damage simulations: Beyond defect production cross-section, displacement per atom and iron-based metrics,” The European Physical Journal Plus. 2019. link Times cited: 22 USED (high confidence) A. Tsukanov, A. Lozhkomoev, M. Lerner, I. Gotman, E. Gutmanas, and S. Psakhie, “Molecular dynamics study of bimetallic Fe–Cu Janus nanoparticles formation by electrical explosion of wires,” Philosophical Magazine. 2019. link Times cited: 3 Abstract: ABSTRACT Bimetallic nanoparticles comprised of two elements … read moreAbstract: ABSTRACT Bimetallic nanoparticles comprised of two elements which are immiscible in the bulk present a unique combination of physical–chemical properties that strongly depend on the atomic arrangement within the particle. In this study, molecular dynamics (MD) simulations of bimetallic Fe–Cu nanoparticles formation by high-velocity collision of individual metal nanoparticles (IMNPs) were performed. Physically these conditions model fast electrical explosion of two metal wires (Fe and Cu). By varying the size, temperature and velocity of colliding IMNPs, the conditions under which phase-segregated Janus nanoparticles are formed were determined. The model predictions showed good agreement with the experimental results. The present work is a step forward to understanding the formation mechanisms of bimetallic nanoparticles with different chemical configurations. read less USED (high confidence) M. R. Karim, M. Kattoura, S. Mannava, V. Vasudevan, A. Malik, and D. Qian, “A computational study on the microstructural evolution in near-surface copper grain boundary structures due to femtosecond laser processing,” Computational Mechanics. 2018. link Times cited: 6 USED (high confidence) M. R. Karim, M. Kattoura, S. Mannava, V. Vasudevan, A. Malik, and D. Qian, “A computational study on the microstructural evolution in near-surface copper grain boundary structures due to femtosecond laser processing,” Computational Mechanics. 2017. link Times cited: 0 USED (high confidence) J. Zhou et al., “Zener pinning by coherent particles: pinning efficiency and particle reorientation mechanisms,” Modelling and Simulation in Materials Science and Engineering. 2017. link Times cited: 13 Abstract: Zener pinning by coherent particles in copper–nickel model a… read moreAbstract: Zener pinning by coherent particles in copper–nickel model alloys has been studied using molecular dynamics simulations. It is found that 4 nm Ni particles were easily cut by migrating Cu grain boundaries during boundary passage, while 7–8 nm particles were harder to cut and coherency-to-incoherency change occurred for some boundaries. Due to low volume fraction and easy cutting, 4 nm particles had a limited pinning effect on grain boundary motion. The increase in volume fraction and the suppressed cutting for 7–8 nm particles caused the boundary motion to be significantly retarded. Different grain boundaries exhibited the distinct ability to move past the same size particle. Significantly, with the pinning effect of Ni particles, misorientation dependence of boundary migration velocity became obvious, which is consistent with the findings in practical materials. During or after passage, the Ni particles were found to change orientation to become coherent with grain growth via various atomistic mechanisms. The mechanisms were discussed with respect to particle size and boundary misorientation. read less USED (high confidence) I. N. Kar’kin, L. E. Kar’kina, P. Korzhavyi, and Y. Gornostyrev, “Monte Carlo simulation of the kinetics of decomposition and the formation of precipitates at grain boundaries of the general type in dilute BCC Fe–Cu alloys,” Physics of the Solid State. 2017. link Times cited: 8 USED (high confidence) W. Cui et al., “Up-Hill Diffusion of Phase-Separated FeCu Melt by Molecular Dynamics Simulation,” Chinese Physics Letters. 2017. link Times cited: 2 USED (high confidence) W. Tucker and P. Schelling, “Thermodiffusion in liquid binary alloys computed from molecular-dynamics simulation and the Green-Kubo formalism,” Computational Materials Science. 2016. link Times cited: 8 USED (high confidence) C. Race, “Quantifying uncertainty in molecular dynamics simulations of grain boundary migration,” Molecular Simulation. 2015. link Times cited: 17 Abstract: Molecular dynamics simulations of simple bicrystal systems h… read moreAbstract: Molecular dynamics simulations of simple bicrystal systems have been much used as a tool to explore how the migration of grain boundaries varies with their structure and with experimental conditions. In order to permit the exploration of a large parameter space, many studies are forced to rely on a small number of simulations (often a single simulation) for each configuration. The motion of a grain boundary is inherently statistical and any variability in the measured grain boundary velocity should be taken into account in subsequent analysis of trends in grain boundary mobility. Here we present the results of large numbers of simulations of equivalent boundaries, which show that this variability can be large, particularly when small systems are simulated. We show how a bootstrap resampling approach can be used to characterise the statistical uncertainty in boundary velocity using the information present in a single simulation. We show that the approach is robust across a variety of system sizes, temperatures and driving force strengths and types, and provides a good order-of-magnitude measure of the population standard deviation across multiple equivalent simulations. read less USED (high confidence) D. Molnár, U. Weber, P. Binkele, D. Rapp, and S. Schmauder, “Prediction of macroscopic damage behaviour of precipitation strengthened steels via multiscale simulations,” GAMM‐Mitteilungen. 2015. link Times cited: 6 Abstract: A multiscale modelling approach is presented that sequential… read moreAbstract: A multiscale modelling approach is presented that sequentially connects in total five simulation methods via parameter transfers in order to capture the macroscopic damage behaviour due to an underlying nano structure of copper precipitates in bcc iron. In this multiscale approach, information on precipitation states is taken from kinetic Monte‐Carlo and Phasefield simulations as well as from experimental data. Based on a calibration of Dislocation Dynamics by Molecular Dynamics simulations as well as on testing conditions known from experiments, Dislocation Dynamics simulations with an infinite dislocation on a single glide plane provide strengthening levels which are related to a reference stress‐strain curve obtained from experiments. Subsequently, the macroscopic damage behaviour is simulated with the Finite‐Element‐Method including the Rousselier Damage Model for the reference state as well as for the virtually aged states. The results are validated by comparison with experimental results and predictions are made with respect to specific precipitation cases. (© 2015 WILEY‐VCH Verlag GmbH & Co. KGaA, Weinheim) read less USED (high confidence) G. Lv, H. Zhang, X. He, W. Yang, and Y. Su, “Atomistic simulation of Cu–Ni precipitates hardening in α-iron,” Journal of Physics D: Applied Physics. 2015. link Times cited: 7 Abstract: In this paper, we investigated the interaction of an edge di… read moreAbstract: In this paper, we investigated the interaction of an edge dislocation with Cu precipitates with a spherical geometry and with Cu–Ni precipitates that possess a Cu core with an outer Ni shell, commonly observed in reactor pressure vessel (RPV) steels. We applied molecular dynamics techniques to explore the critical stress required to unpin the dislocation (CSRUD), the breakaway dislocation line shape when the dislocation leaves the precipitates and the transition of Cu atoms within precipitates. The results indicate that the CSRUD of the Cu–Ni precipitates with a diameter less than 2.38 nm is larger than that of Cu precipitates that contain the same number of Cu atoms, while for a diameter larger than 2.38 nm, the CSRUD of Cu–Ni precipitates is weaker, which is related to the bcc to fcc-like or hcp-like atoms transformation in precipitates. The dislocations interact with Cu and Cu–Ni precipitates via the cut mechanism. read less USED (high confidence) L. Shao et al., “Sink property of metallic glass free surfaces,” Scientific Reports. 2015. link Times cited: 18 USED (high confidence) S. Vigonski, F. Djurabekova, M. Veske, A. Aabloo, and V. Zadin, “Molecular dynamics simulations of near-surface Fe precipitates in Cu under high electric fields,” Modelling and Simulation in Materials Science and Engineering. 2015. link Times cited: 14 Abstract: High electric fields in particle accelerators cause vacuum b… read moreAbstract: High electric fields in particle accelerators cause vacuum breakdowns in the accelerating structures. The breakdowns are thought to be initiated by the modification of material surface geometry under high electric fields. These modifications in the shape of surface protrusions enhance the electric field locally due to the increased surface curvature. Using molecular dynamics, we simulate the behaviour of Cu containing a near-surface Fe precipitate under a high electric field. We find that the presence of a precipitate under the surface can cause the nucleation of dislocations in the material, leading to the appearance of atomic steps on the surface. Steps resulting from several precipitates in close proximity can also form protruding plateaus. Under very high external fields, in some cases, we observed the formation of voids above or below the precipitate, providing additional dislocation nucleation sites. read less USED (high confidence) S. Shao, J. Wang, and A. Misra, “Energy minimization mechanisms of semi-coherent interfaces,” Journal of Applied Physics. 2014. link Times cited: 51 Abstract: In this article, we discussed energy minimization mechanisms… read moreAbstract: In this article, we discussed energy minimization mechanisms of semi-coherent interfaces based on atomistic simulations and dislocation theory. For example, of {111} interfaces between two face centered cubic (FCC) crystals, interface comprises of two stable structures (normal FCC stacking structure and intrinsic stacking fault structure), misfit dislocations, and misfit dislocation intersections or nodes (corresponding to the high energy stacking fault (HESF) structure). According to atomistic simulations of four interfaces, we found that (1) greater spacing between misfit dislocations and/or larger slopes of generalized stacking fault energy at the stable interface structures leads to a narrower dislocation core and a higher state of coherency in the stable interfaces; (2) the HESF region is relaxed by the relative rotation and dilation/compression of the two crystals at the node. The crystal rotation is responsible for the spiral feature at the vicinity of a node and the dilation/compression is responsible for the creation of the free volume at a node; (3) the spiral feature is gradually frail and the free volume decreases with decreasing misfit dislocation spacing, which corresponds to an increase in lattice mismatch and/or a decrease in lattice rotation. Finally, the analysis method and energy minimization mechanisms explored in FCC {111} semi-coherent interfaces are also applicable for other semi-coherent interfaces. read less USED (high confidence) Y. Satoh, H. Abe, and T. Matsunaga, “Radiation-induced glide motion of interstitial clusters in concentrated alloys,” Philosophical Magazine. 2014. link Times cited: 4 Abstract: We propose a mechanism for glide motion, i.e. one-dimensiona… read moreAbstract: We propose a mechanism for glide motion, i.e. one-dimensional (1D) migration, of interstitial clusters in concentrated alloys driven by high-energy particle irradiation. Interstitial clusters are fundamentally mobile on their respective 1D migration tracks, but in concentrated random alloys they are stationary at the position where the fluctuating formation energy achieves a local minimum. Irradiation changes the microscopic distribution of solute atoms through atomic displacement and recovery of the produced Frenkel pairs, which causes cluster 1D migration into a new stable position. In molecular dynamics simulations of interstitial clusters up to 217i in Fe–Cu alloys, stepwise 1D migration was observed under interatomic mixing or shrinkage of the cluster: a single 1D migration was induced by two exchanges per atom or cluster radius change by two interatomic distances. The 1D migration distance ranged up to several nanometers. We compared the frequency and distance of 1D migration with those for in situ observation using high-voltage electron microscopy, allowing for the extremely large rate of interatomic mixing and cluster shrinkage in the present simulation. read less USED (high confidence) T. Rupert, “Solid Solution Strengthening and Softening Due to Collective Nanocrystalline Deformation Physics,” arXiv: Materials Science. 2014. link Times cited: 34 USED (high confidence) S. Shao, J. Wang, A. Misra, and R. Hoagland, “Spiral Patterns of Dislocations at Nodes in (111) Semi-coherent FCC Interfaces,” Scientific Reports. 2013. link Times cited: 91 USED (high confidence) D. Molnár, P. Binkele, S. Hocker, and S. Schmauder, “Atomistic multiscale simulations on the anisotropic tensile behaviour of copper-alloyed alpha-iron at different states of thermal ageing,” Philosophical Magazine. 2012. link Times cited: 18 Abstract: The mechanical behaviour of steels is strongly related to th… read moreAbstract: The mechanical behaviour of steels is strongly related to their underlying atomistic structures which evolve during thermal treatment. Cu-alloyed α-Fe undergoes a change in material behaviour during the ageing process, especially at temperatures of above 300°C, where precipitates form on a large time-scale within the α-Fe matrix, yielding first a precipitation strengthening of the material. As the precipitates grow further in time, the material strength decreases again. This complex process is modelled with a multiscale approach, combining Kinetic Monte Carlo (KMC) with Molecular Dynamics (MD) simulations in a sequential way and exploiting the advantages of both methods while simultaneously circumventing their particular disadvantages. The formation of precipitates is modelled on a single-crystal lattice with a diffusion based KMC approach. Transferring selected precipitation states at different ageing times to MD simulations allows the performance of nano tensile tests and the analysis of failure initiation. The anisotropic tensile behaviour is investigated in the [100], [110] and [111] directions, showing monotonically decreasing tensile strengths and deformation strains. Hence precipitation strengthening is mainly due to dislocation–precipitate interactions which are non-existent at small tensile loadings in this scenario. At the point of ductile failure, dislocations are generated at the interfaces between precipitates and the Fe matrix. Straining in the [100] direction, they lie on {110} and {112} glide planes, as expected. With the method presented here, the changes of the anisotropic tensile moduli are related to different states of thermal ageing, i.e., to nucleation, growth and Ostwald ripening of Cu precipitates. read less USED (low confidence) S. Kumar, A. Rajput, S. K. Paul, M. Tiwari, and D. K. Prajapati, “Friction and wear study of metallic contacts under dry sliding conditions: A molecular dynamics simulation-based approach,” Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology. 2023. link Times cited: 0 Abstract: Sliding friction originating due to ploughing and adhesive w… read moreAbstract: Sliding friction originating due to ploughing and adhesive wear significantly affects the performance of small-scale components, that is, nano-electromechanical systems/micro-electromechanical. To get a comprehensive understanding of the friction mechanisms, a comprehensive study of surface interactions at the nanoscale is crucial, particularly when dealing with nano-electromechanical and micro-electromechanical components. This study performed molecular dynamics simulation to explore the interactions between asperities (made of similar/dissimilar materials) at the nanoscale under dry sliding conditions. The research framework focuses on modelling the contact between two hemispherical asperities during dry sliding by considering three material combinations: soft-to-soft (Cu–Cu), hard-to-hard (Fe–Fe), and hard-to-soft (Fe–Cu). The study assesses plastic deformation and atomic wear at specific sliding speeds. Notably, the results indicate that the frictional force on the lower asperity increases as interference increases. Additionally, atomic wear rises with increased interference in the case of the Fe–Cu tribopair. Particularly high atomic wear is observed in the Cu–Cu tribopair due to the ease of slip within the face-centred cubic crystal structure of copper. read less USED (low confidence) Y. He, Z. Gao, M. Tang, X. Sun, P. Gao, and J. Sun, “Characteristics of atomic removal and mechanism of damage formation in vibration-assisted nano cutting of copper-nickel alloy,” Materials Today Communications. 2023. link Times cited: 0 USED (low confidence) X. Zhu, X. Wang, Y. Liu, Y. Luo, and H. Zhang, “Probing the Effect of Cuttings Particle Size on the Friction and Wear Mechanism at the Casing Friction Interface: A Molecular Dynamics Study.,” Langmuir : the ACS journal of surfaces and colloids. 2023. link Times cited: 0 Abstract: Cuttings particles of different sizes in the drilling fluid … read moreAbstract: Cuttings particles of different sizes in the drilling fluid are the leading cause of wear at the casing and drill pipe joints, and diamond-like carbon (DLC) films have excellent research potential in reducing tool wear due to their ultra-low friction coefficient and high wear resistance. In this paper, a corresponding molecular dynamics model was developed using LAMMPS to investigate the effect of silica particles of different particle sizes on the friction and wear mechanisms of Fe/DLC friction pairs at the microscale. The results show that small cuttings particles in a dry environment are more likely to cause interface wear between the casing and drill pipe joint, while in a water environment, the opposite is true. The main reason is that small particles in a dry environment have smaller contact areas and greater indentation depth, leading to greater wear at the friction interface. The movement of water molecules in the water environment will promote the composite movement of large particles, thereby exacerbating the wear of the interface. Moreover, the relevant research results at the micro-scale indicate that DLC films can effectively reduce wear, which provides theoretical support for its application in drill pipe joints. read less USED (low confidence) A. Kumar, R. Kumar, S. Kumar, and A. K. V, “Atomistic structural transformation of Fe-Cr-Ni single crystal alloy under uniaxial deformation using molecular dynamics simulation,” Materials Today: Proceedings. 2023. link Times cited: 0 USED (low confidence) D. Tramontina et al., “Probing radiation resistance in simulated metallic core–shell nanoparticles,” Computational Materials Science. 2023. link Times cited: 0 USED (low confidence) T. Zhou, Y. Wu, and J.-J. You, “Evolution of the shape and microstructure of body-centered cubic seeds during Cu melt solidification,” Chemical Physics Letters. 2023. link Times cited: 0 USED (low confidence) N. Wang et al., “An experimental and molecular dynamics study on the formation of low-energy grain boundaries induced by grain rotation during rapid solidification,” Materials Letters. 2023. link Times cited: 0 USED (low confidence) W. Pang, X.-jing Feng, R. Chen, A. Liu, and K. Xin, “Molecular dynamics studies of the effect of intermediate Fe layer thickness on the enhanced strength and ductility of Cu/Fe/Ni multilayer,” Physica Scripta. 2023. link Times cited: 0 Abstract: The synergistic strength-ductility is very important for com… read moreAbstract: The synergistic strength-ductility is very important for composite materials. In this work, we studied the effect of intermediate layer thickness on the mechanical properties of Cu/Fe/Ni multilayer by introducing harder intermediate layer and non-coherent interface using molecular dynamics simulation, and revealed the relationship between the deformation mechanism and the strength-ductility from atomic scale. The results show that the yield strength and flow stress increase with increasing Fe layer thickness, but the tensile strain is opposite. Plastic deformation of all models are triggered by slipping of misfit partial dislocation originating from the decomposition of perfect dislocation on semi-coherent interface. However, the addition of Fe layer and non-coherent interface increases the resistance of dislocation crossing interface, and changes the dominant deformation mechanism from Shockley partial dislocation slipping to deformation twinning migration, thus improving the strength and ductility of multilayer. In addition, the evolution laws of the dislocation length and interface morphology as well as the shear strain distribution are discussed. read less USED (low confidence) R. Barik, S. Biswal, A. Dutta, D. Chakrabarti, and A. Ghosh, “Effect of solute distribution on the screw dislocation motion in bcc Fe-based systems,” Computational Materials Science. 2023. link Times cited: 0 USED (low confidence) A. Dmitriev and A. Nikonov, “Molecular-Dynamic Study of the Interfacial Zone of Dissimilar Metals Under Compression and Shear,” Russian Physics Journal. 2023. link Times cited: 0 USED (low confidence) S. Yang, H. Bao, H. Bai, Y. Li, H. Xu, and F. Ma, “Effects of Fe solid solute on grain boundaries of bi-crystal Cu: A molecular dynamics simulation,” Nano Materials Science. 2023. link Times cited: 0 USED (low confidence) F. Wang et al., “Enhanced nanocrystalline stability of BCC iron via copper segregation,” Progress in Natural Science: Materials International. 2023. link Times cited: 4 USED (low confidence) “A physically-based constitutive model for a novel heat resistant martensitic steel under different cyclic loading modes: Microstructural strengthening mechanisms,” International Journal of Plasticity. 2023. link Times cited: 12 USED (low confidence) B. Li, R. Ma, S. Qin, and X. Zhang, “Regulating the dislocation-nanocluster interactions by electrical pulses to alleviate material hardening,” Materials Science and Engineering: A. 2023. link Times cited: 0 USED (low confidence) K. Bandyopadhyay, S. Das, K. S. Ghosh, and M. Ghosh, “Molecular Dynamics-Based Scheme of Designing Nanostructured Cu-Ni Alloy Thin Film for Coating on Advanced Structural Components in Naval Vessels,” Journal of Materials Engineering and Performance. 2022. link Times cited: 2 USED (low confidence) Y. Lei et al., “An Embedded-Atom Method Potential for studying the properties of Fe-Pb solid-liquid interface,” Journal of Nuclear Materials. 2022. link Times cited: 1 USED (low confidence) G. Zhang, M. Wang, H. Yu, H. Xu, and A. Wan, “Molecular Dynamics and Experimental Investigation on the Interfacial Binding Mechanism in the Fe/Cu1−x-Nix Bimetallic Interface,” Nanomaterials. 2022. link Times cited: 0 Abstract: To systematically investigate the diffusion behavior of Fe/C… read moreAbstract: To systematically investigate the diffusion behavior of Fe/Cu bimetallic materials and the influence of the Ni element on the diffusion and mechanical properties of the Fe/Cu bimetallic interface, the diffusion distance, diffusion coefficient, and strain–stress process based on molecular dynamics (MD) calculations and experimental testing were analyzed. All simulation results indicated that the liquid Cu matrix had a higher diffusion coefficient but hardly diffused into the Fe matrix, and the solid Fe matrix had a smaller diffusion coefficient but diffused deep into the Cu matrix at the same temperature. Compared with the initial state, the addition of nickel atoms to the Cu matrix favored the improvement of the diffusion coefficient and the diffusion distance of Fe/Cu bimetallic materials. Moreover, we found that the diffusion distance and the yield strength simultaneously increased and then decreased with the increase in Ni atoms, which is in agreement with the experimental test results. These improvements in the diffusion and mechanical properties were attributed to the enrichment of Ni atoms at the interface, but excessive Ni content resulted in deteriorated properties. Finally, our research described the enhancement mechanism of the addition of nickel atoms to the Fe/Cu bimetallic diffusion system. An analysis of the contributions of the diffusion distance, the diffusion coefficient, and the yield strength revealed that the diffusion properties of nickel atoms play an important role in Fe/Cu bimetallic materials. read less USED (low confidence) K. Ren, L. Liu, J. Li, H. Pan, and Z. Wang, “Lubrication Behavior of n-hexadecane on ZnO Layer at the Nanoscale: A Molecular Dynamic Exploration,” Tribology Letters. 2022. link Times cited: 1 USED (low confidence) G. Dai, S. Wu, X. Huang, M.-jie Wang, and X. Teng, “Thermal diffusion behavior of Fe/Cu/Ni multilayer coatings: a molecular dynamics study,” Modelling and Simulation in Materials Science and Engineering. 2022. link Times cited: 1 Abstract: In this paper, the thermal diffusion behavior of Fe/Cu/Ni mu… read moreAbstract: In this paper, the thermal diffusion behavior of Fe/Cu/Ni multilayer coatings was investigated by molecular dynamics. The results show that the Fe, Cu, and Ni elements can diffuse each other at 1250 K. Meanwhile, the intrinsic diffusion coefficients and interdiffusion coefficients of the Fe, Cu, and Ni were calculated. Besides, the diffusion mechanism for high melting-point elements of Fe and Ni at 1250 K was analyzed in the paper. According to the simulation result, the Fe and Ni lattices were disturbed by the active Cu particles. Fe and Ni particles at higher energies may move out of their original positions and migrate into the Cu lattice randomly. Thus, the Fe and Ni elements were involved in the thermal diffusion. This can be confirmed by the decrease of the peak and the disappearance of the secondary peak in the radial distribution function curves. However, the position of the curve peaks did not change. Thus, the lattice structure was still maintained during the whole diffusion process. The thermal diffusion of the three elements was carried out by particle substitution at the lattice positions. It was a solid phase diffusion process. Furthermore, there was a clear particle diffusion asymmetry at the original interface of the element. It was consistent with the diffusion asymmetry of diffusion-couple experiments. The primary reason for this diffusion asymmetry was the difference in the interaction potential of the three elements. This asymmetry was ultimately reflected in the intrinsic diffusion coefficient and the interdiffusion coefficient of each element. For the Fe–Cu–Ni ternary system, the largest diffusion coefficient was copper and the smallest was iron at 1250 K. read less USED (low confidence) Y. Deng et al., “Molecular dynamics simulation of the growth and diffusion mechanisms of Fe–Cu bimetallic nanoparticles,” Philosophical Magazine. 2022. link Times cited: 1 Abstract: ABSTRACT In accordance with the molecular dynamic simulation… read moreAbstract: ABSTRACT In accordance with the molecular dynamic simulation and nudged elastic band method, the surface diffusion and growth of Fe–Cu nanoparticles were studied, respectively, using Large-scale Atomic/Molecular Massively Parallel Simulator code. Results showed that a single Cu adatom diffused on the surface of the Fe substrate mainly via the hopping mechanism and nearly did not exchange with the substrate atoms. In the Cu substrate, when interfacet diffusion of a Fe adatom on the surface was activated, the system energy evidently decreased after the exchange mechanism was chosen. At low temperatures, the metastable core–shell structure of FeshellCucore nanoparticles was obtained by simulating the deposition of Fe on Cu substrate. For the growth of Cu on Fe substrate, FecoreCushell nanoparticles could be formed and they gradually evolved into Wulff-like structures with depositing Cu atoms. The Monte Carlo calculation further showed that the stable configuration of Fe–Cu nanoparticles is FecoreCushell when the concentration of Cu atoms is small. With the increase of Cu atomic ratio (enough to cover the surface), the quasi-Janus was the stable structure in Fe–Cu nanoparticles. read less USED (low confidence) D. Yang, H. Liu, Q. Jiang, Y. Jiang, X. Wang, and W. Yang, “Atomic-level understanding of weakening crystallization in additive manufactured ternary Fe-based metallic glasses with Ni addition,” Journal of Non-Crystalline Solids. 2022. link Times cited: 5 USED (low confidence) H. Bao, H. Xu, Y. Li, H. Bai, and F. Ma, “The interaction mechanisms between dislocations and nano-precipitates in CuFe alloys: a molecular dynamic simulation,” International Journal of Plasticity. 2022. link Times cited: 11 USED (low confidence) J. Syarif, V. Gillette, H. Hussien, K. Badawy, and N. Jisrawi, “Molecular dynamics simulation of the amorphization and alloying of a mechanically milled Fe-Cu system,” Journal of Non-Crystalline Solids. 2022. link Times cited: 1 USED (low confidence) I. Camacho et al., “On the anticorrosion mechanism of molten salts based nanofluids,” Solar Energy Materials and Solar Cells. 2022. link Times cited: 5 USED (low confidence) Z. Shi, B. Li, and Z. Sun, “Study on microstructure evolution of grinding surface of bcc Fe-Ni maraging steel based on molecular dynamics,” Applied Surface Science. 2022. link Times cited: 7 USED (low confidence) A. Mishra, J. Lind, M. Kumar, and A. Dongare, “Understanding the phase transformation mechanisms that affect the dynamic response of Fe-based microstructures at the atomic scales,” Journal of Applied Physics. 2021. link Times cited: 8 USED (low confidence) J. Yin, H. Hou, J. Wang, X. Liu, and F. Xue, “Atomistic simulation of [100](001) crack propagation with Cu precipitates in α-iron,” International Journal of Pressure Vessels and Piping. 2021. link Times cited: 4 USED (low confidence) C. Yi, C. Hu, L. Shi, M.-li Bai, and J. Lv, “Wettability of complex Long-Chain alkanes droplets on Pillar-type surfaces,” Applied Surface Science. 2021. link Times cited: 4 USED (low confidence) D. S. Sineglazov, S. Divinski, and A. V. Pokoev, “Simulation of the Magnetoplastic Effect in a Cu–Ni Alloy,” Journal of Surface Investigation: X-ray, Synchrotron and Neutron Techniques. 2021. link Times cited: 0 USED (low confidence) X.-jing Feng, Z. Lin, K. Xin, and W. Pang, “The deformation mechanisms and mechanical properties of Cu/Fe multilayer during compression process,” Journal of Materials Research. 2021. link Times cited: 4 Abstract: The deformation mechanisms and mechanical properties of Cu/F… read moreAbstract: The deformation mechanisms and mechanical properties of Cu/Fe multilayer during compression process are investigated via atomistic simulations and rationalized analysis. It is found that yield stress and strain of Kurdjumov–Sachs model are lower than that of Nishiyama–Wassermann model, and lattice dislocation nucleates from periodic arrangement structures on the interface. We present that preferred slip systems are dominated not only by Schmidt factors but also by intersection line orientations of slip system on the interface, as well as angles between activated slip system of Cu layer and slip system of Fe layer. During deformation process, extended full dislocation dominates deformation behavior of Cu layer, and perfect dislocation and twinning dominate deformation behavior of Fe layer. After deformation, tetrahedral structures and point defects form on Cu side of interface and inside Fe layer, respectively. We calculate evolution curves for number of dislocation segments and interface thickness to illuminate deformation behavior. read less USED (low confidence) X. Li, Z.-an Tian, Q. Xie, and K. Dong, “The topologically close-packed Fe70Cu15Ni15 nanoparticles- A simulation study,” Vacuum. 2021. link Times cited: 3 USED (low confidence) X.-Y. Liu, L. Capolungo, and A. Hunter, “Screw dislocation impingement and slip transfer at fcc-bcc semicoherent interfaces,” Scripta Materialia. 2021. link Times cited: 9 USED (low confidence) H. Xu, H. Bao, Y. Li, H. Bai, and F. Ma, “Atomic scale insights into the rapid crystallization and precipitation behaviors in FeCu binary alloys,” Journal of Alloys and Compounds. 2021. link Times cited: 5 USED (low confidence) Y. Li et al., “Shear-strain induced structural relaxation of Cu Σ3 [110](112) symmetric tilt grain boundary: The role of foreign atoms and temperature,” Current Applied Physics. 2021. link Times cited: 1 USED (low confidence) N. Eom, M. Messing, J. Johansson, and K. Deppert, “General Trends in Core–Shell Preferences for Bimetallic Nanoparticles,” ACS Nano. 2021. link Times cited: 36 Abstract: Surface segregation phenomena dictate core–shell preference … read moreAbstract: Surface segregation phenomena dictate core–shell preference of bimetallic nanoparticles and thus play a crucial role in the nanoparticle synthesis and applications. Although it is generally agreed that surface segregation depends on the constituent materials’ physical properties, a comprehensive picture of the phenomena on the nanoscale is not yet complete. Here we use a combination of molecular dynamics (MD) and Monte Carlo (MC) simulations on 45 bimetallic combinations to determine the general trend on the core–shell preference and the effects of size and composition. From the extensive studies over sizes and compositions, we find that the surface segregation and degree of the core–shell tendency of the bimetallic combinations depend on the sufficiency or scarcity of the surface-preferring material. Principal component analysis (PCA) and linear discriminant analysis (LDA) on the molecular dynamics simulations results reveal that cohesive energy and Wigner–Seitz radius are the two primary factors that have an “additive” effect on the segregation level and core–shell preference in the bimetallic nanoparticles studied. When the element with the higher cohesive energy also has the larger Wigner–Seitz radius, its core preference decreases, and thus this combination forms less segregated structures than what one would expect from the cohesive energy difference alone. Highly segregated structures (highly segregated core–shell or Janus-like) are expected to form when both the relative cohesive energy difference is greater than ∼20%, and the relative Wigner–Seitz radius difference is greater than ∼4%. Practical guides for predicting core–shell preference and degree of segregation level are presented. read less USED (low confidence) J. Syarif and K. Badawy, “Computational modelling of cold rolling of ferritic iron containing ε-Cu precipitates,” Materials today communications. 2021. link Times cited: 0 USED (low confidence) F. Tan, F. Li, Q. Fang, J. Li, and H. Feng, “Grain boundary migration and deformation mechanism influenced by heterogeneous precipitate,” Journal of Materials Science. 2021. link Times cited: 2 USED (low confidence) S. Eder, P. Grützmacher, M. R. Ripoll, and J. Belak, “Elucidating the Onset of Plasticity in Sliding Contacts Using Differential EBSD Tomography.” 2021. link Times cited: 0 Abstract:
Depending on the mechanical and thermal energy introduced … read moreAbstract:
Depending on the mechanical and thermal energy introduced to a dry sliding interface, the near-surface regions of the mated bodies may undergo plastic deformation. In this work, we use "differential EBSD tomography" to highlight changes to the microstructure near tribological fcc alloy surfaces, allowing us to detect subtle differences in lattice orientation and small distances in grain boundary migration. The analysis approach compares electron backscatter diffraction images generated from large-scale molecular dynamics simulations with their undeformed counterparts via a simple image analysis filter. We use our visualization method to discuss the acting microstructural mechanisms in a load- and time-resolved fashion, focusing on sliding conditions that lead to twinning, partial lattice rotation, and grain boundary dominated processes. Extracting and laterally averaging the color saturation value of the generated tomographs allows us to produce quantitative time- and depth-resolved maps that give a good overview of the progress and severity of near-surface deformation. Corresponding maps of the lateral standard deviation in the color saturation show evidence of homogenization processes occurring in the tribologically loaded microstructure, frequently leading to the formation of a well-defined separation between deformed and undeformed regions. When integrated into a computational materials engineering framework, our approach could help optimize material design for tribological and other deformation problems. read less USED (low confidence) Z. Lin, W. Pang, K. Xin, X.-jing Feng, and F. Yin, “The effect of loading strain rates on deformation behavior of Cu/Fe composite,” Physics Letters A. 2021. link Times cited: 5 USED (low confidence) S. Eder, P. Grützmacher, M. R. Ripoll, D. Dini, and C. Gachot, “Effect of Temperature on the Deformation Behavior of Copper Nickel Alloys under Sliding,” Materials. 2020. link Times cited: 18 Abstract: The microstructural evolution in the near-surface regions of… read moreAbstract: The microstructural evolution in the near-surface regions of a dry sliding interface has considerable influence on its tribological behavior and is driven mainly by mechanical energy and heat. In this work, we use large-scale molecular dynamics simulations to study the effect of temperature on the deformation response of FCC CuNi alloys of several compositions under various normal pressures. The microstructural evolution below the surface, marked by mechanisms spanning grain refinement, grain coarsening, twinning, and shear layer formation, is discussed in depth. The observed results are complemented by a rigorous analysis of the dislocation activity near the sliding interface. Moreover, we define key quantities corresponding to deformation mechanisms and analyze the time-independent differences between 300 K and 600 K for all simulated compositions and normal pressures. Raising the Ni content or reducing the temperature increases the energy barrier to activate dislocation activity or promote plasticity overall, thus increasing the threshold stress required for the transition to the next deformation regime. Repeated distillation of our quantitative analysis and successive elimination of spatial and time dimensions from the data allows us to produce a 3D map of the dominating deformation mechanism regimes for CuNi alloys as a function of composition, normal pressure, and homologous temperature. read less USED (low confidence) H. Wang, X. Gao, S. Chen, L. Yiming, Z.-wang Wu, and H. Ren, “Effects of Al on the precipitation of B2 Cu-rich particles in Fe–Cu ferritic alloy: Experimental and theoretical study,” Journal of Alloys and Compounds. 2020. link Times cited: 5 USED (low confidence) A. Garrett and C. Race, “Cu nanoprecipitate morphologies and interfacial energy densities in bcc Fe from density functional theory (DFT),” Computational Materials Science. 2020. link Times cited: 7 USED (low confidence) J. Li, Z.-an Tian, Q. Xie, and S. Xiong, “Component effect on microstructure of rapidly cooled FeCuNi alloys,” Chemical Physics Letters. 2020. link Times cited: 4 USED (low confidence) M. Ghaemi and R. Tavakoli, “Universal correlation between the thermodynamic potentials and some physical quantities of metallic glasses as a function of cooling rate during molecular dynamics simulation,” Journal of Non-crystalline Solids. 2020. link Times cited: 2 USED (low confidence) B. Yao and R. F. Zhang, “AADIS: An atomistic analyzer for dislocation character and distribution,” Comput. Phys. Commun. 2020. link Times cited: 19 USED (low confidence) S. Kumar, “Structural Evolution of Iron–Copper (Fe–Cu) Bimetallic Janus Nanoparticles during Solidification: An Atomistic Investigation,” Journal of Physical Chemistry C. 2020. link Times cited: 15 Abstract: Bimetallic nanoparticles consist of two different metallic e… read moreAbstract: Bimetallic nanoparticles consist of two different metallic elements, which have attracted enormous interest from both the scientific and industrial points of view. Bimetallic nanoparticles could de... read less USED (low confidence) Z. Sun, F. Z. Dai, B. Xu, and W.-Z. Zhang, “Dislocation-mediated migration of interphase boundaries,” Journal of Materials Science & Technology. 2019. link Times cited: 7 USED (low confidence) J. Yin, Y. Wang, H. Hou, J. Wang, X. Liu, and F. Xue, “Atomistic simulation of interactions between an edge dislocation and Cu precipitates with different chemical compositions in α-Fe,” Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms. 2019. link Times cited: 4 USED (low confidence) J. Chen et al., “Dynamics simulation study on crystallization of amorphous Ni-Fe alloy,” Ferroelectrics. 2019. link Times cited: 1 Abstract: Molecular dynamics simulation was performed to study the cry… read moreAbstract: Molecular dynamics simulation was performed to study the crystallization of warming in Ni-Fe alloy. The results show that the crystallization temperature of amorphous Ni-Fe alloy is approximate 800 K–1000 K with the temperature increasing. We proved the crystallization temperature increases as the heating rate increases. In the crystallization stage, the lattice structure ratios generated is different with the different temperatures, it is because of the crystallization temperature determines the lattice structure. Moreover, we found that the best temperature for crystallization of Ni-Fe alloy, and at the optimum crystallization temperature the face-centered cubic reaches 68.8%. read less USED (low confidence) M. Hummel, C. Böhm, W. Verestek, and S. Schmauder, “Introducing a method of constructing realistic closed cell nano-porous iron crystals and MD simulations to investigate the influence of the system size on the stability and the mechanical properties,” Computational Materials Science. 2019. link Times cited: 4 USED (low confidence) H. Luu and N. Gunkelmann, “Pressure-induced phase transformations in Fe-C: Molecular dynamics approach,” Computational Materials Science. 2019. link Times cited: 24 USED (low confidence) G. Bonny, C. Domain, N. Castin, P. Olsson, and L. Malerba, “The impact of alloying elements on the precipitation stability and kinetics in iron based alloys: An atomistic study,” Computational Materials Science. 2019. link Times cited: 27 USED (low confidence) L. Li, Q. Fang, J. Li, and H. Wu, “Origin of strengthening-softening trade-off in gradient nanostructured body-centred cubic alloys,” Journal of Alloys and Compounds. 2019. link Times cited: 12 USED (low confidence) C. Zhang, K. Ma, N. Zhao, and Z. Yuan, “A Core–Shell Strategy for Improving Alloy Catalyst Activity for Continual Growth of Hollow Carbon Onions,” Crystal Growth & Design. 2018. link Times cited: 9 Abstract: Herein, we report the controlled synthesis of hollow carbon … read moreAbstract: Herein, we report the controlled synthesis of hollow carbon nano-onions (HCNOs) through using core–shell Fe-Ni alloy catalysts. The core–shell structure is formed through the phase transition during the thermal treatment under hydrogen. The inner γ-Fe-Ni core shows the catalytic activity in growing HCNOs, whereas the outer shell is catalytically inert and acts as the protective layer, which can also be converted to the inner core during the growth. This continuous supply of active metallic atoms from the outer shell to the inner catalyst can in situ maintain the catalytic activity, avoiding the use of additional oxygen-containing oxidative agents. In addition, the shell-to-core conversion can be well controlled by tuning hydrogen flow rates during the chemical vapor deposition process to enable a continual growth of HCNOs from one catalyst. Furthermore, the size-controlled growth can be realized by controlling the size of the catalyst nanoparticles. This controlled shell-to-core conversion allows for the ... read less USED (low confidence) H. N. Pishkenari, F. S. Yousefi, and A. Taghibakhshi, “Determination of surface properties and elastic constants of FCC metals: a comparison among different EAM potentials in thin film and bulk scale,” Materials Research Express. 2018. link Times cited: 22 Abstract: Three independent elastic constants C11, C12, and C44 were c… read moreAbstract: Three independent elastic constants C11, C12, and C44 were calculated and compared using available potentials of eight different metals with FCC crystal structure; Gold, Silver, Copper, Nickel, Platinum, Palladium, Aluminum and Lead. In order to calculate the elastic constants, the second derivative of the energy density of each system was calculated with respect to different directions of strains. Each set of the elastic constants of the metals in bulk scale was compared with experimental results, and the average relative error was for each was calculated and compared with other available potentials. Then, using the Voigt-Reuss-Hill method, approximated values for Young and shear moduli and Poisson’s ratio of the FCC metals in the bulk scale were found for each potential. Furthermore, to observe the surface effects on the metals in nanoscale, surface elastic constants of the thin films of the metals have been calculated. In the study of the thin films of materials in nanoscale, the number of surface atoms is considerable compared to all atoms of the object. This leads to an increase in the surface effects, which influence the elastic properties. By considering this fact and employing related definitions and equations, the properties of the thin films of the metals were calculated, and the surface effects for different crystallographic directions were compared. Subsequently, in some cases, comparisons among characteristics of the metals in the thin film and bulk material were made. read less USED (low confidence) Y. Zhang, D. Schwen, and X. Bai, “Effects of solute-SIA binding energy on defect production behaviors in Fe-based alloys,” Journal of Nuclear Materials. 2018. link Times cited: 6 USED (low confidence) Q. Fang, L. Li, J. Li, and H. Wu, “Strengthening mechanism of gradient nanostructured body-centred cubic iron film: From inverse Hall-Petch to classic Hall-Petch,” Computational Materials Science. 2018. link Times cited: 19 USED (low confidence) P. M. Sepúlveda et al., “As(V) removal capacity of FeCu bimetallic nanoparticles in aqueous solutions: The influence of Cu content and morphologic changes in bimetallic nanoparticles.,” Journal of colloid and interface science. 2018. link Times cited: 53 USED (low confidence) S. Eder, U. Cihak-Bayr, C. Gachot, and M. R. Ripoll, “Interfacial Microstructure Evolution Due to Strain Path Changes in Sliding Contacts.,” ACS applied materials & interfaces. 2018. link Times cited: 16 Abstract: We performed large-scale molecular dynamics (MD) simulations… read moreAbstract: We performed large-scale molecular dynamics (MD) simulations to study the transient softening stage that has been observed experimentally in sliding interfaces subject to strain path changes. The occurrence of this effect can be of crucial importance for the energy efficiency and wear resistance of systems that experience changes in the sliding direction, such as bearings or gears in wind parks, piston rings in combustion engines, or wheel-rail contacts for portal cranes. We therefore modeled the sliding of a rough counterbody against two polycrystalline substrates of face-centered cubic (fcc) copper and body-centered cubic (bcc) iron with initial near-surface grain sizes of 40 nm. The microstructural development of these substrates was monitored and quantified as a function of time, depth, and applied pressure during unidirectional sliding for 7 ns. The results were then compared to the case of sliding in one direction for 5 ns and reversing the sliding direction for an additional 2 ns. We observed the generation of partial dislocations, grain refinement, and rotation as well as twinning (for fcc) in the near-surface region. All microstructures were increasingly affected by these processes when maintaining the sliding direction but recovered to a great extent upon sliding reversal up to applied pressures of 0.4 GPa in the case of fcc Cu and 1.5 GPa for bcc Fe. We discuss the applicability and limits of our polycrystalline MD model for reproducing well-known bulk phenomena such as the Bauschinger effect in interfacial processes. read less USED (low confidence) N. Castin et al., “Advanced atomistic models for radiation damage in Fe-based alloys: Contributions and future perspectives from artificial neural networks,” Computational Materials Science. 2018. link Times cited: 21 USED (low confidence) A. Gola, P. Gumbsch, and L. Pastewka, “Atomic-scale simulation of structure and mechanical properties of Cu1−xAgx|Ni multilayer systems,” Acta Materialia. 2018. link Times cited: 17 USED (low confidence) W. Cui, L. Wang, C. Peng, and K. Song, “Phase separation and structure transition of undercooled Fe75Cu25 melts,” Physics and Chemistry of Liquids. 2018. link Times cited: 2 Abstract: ABSTRACT The rapid quenching processes of Fe75Cu25 melt at d… read moreAbstract: ABSTRACT The rapid quenching processes of Fe75Cu25 melt at different cooling rate are investigated by molecular dynamics simulation based on embedded atom method. Fe75Cu25 alloy ribbons are prepared by single roller rapid quenching. Liquid–liquid phase separation (LLPS) happens and the Cu-rich droplets embedded in the Fe-rich matrix can be observed both in simulation and experiments. Stronger interaction of homogeneous atom pairs than that of heterogeneous atom pairs leads to LLPS, controlled by nucleation growth mechanism in Fe75Cu25 melt, and quite different from that in Fe50Cu50 melt, which is controlled by spinodal decomposition mechanism. During the crystallisation process after LLPS, the new nuclei form only in Fe-rich regions; various multiply twinning boundaries are formed due to the minimisation of interfacial energy and only the homogeneous atomic stacking shows mirror symmetry along twinning boundary. The results provide atomic-scale understanding of phase separation mechanism and structure transition of Fe75Cu25 melt during rapid cooling processes. read less USED (low confidence) J. Lu, S. Ma, X.-X. Wang, and S. Wang, “The cluster-plus-glue-atom models of solid solution CuNi alloys: A first-principles study,” Computational Materials Science. 2018. link Times cited: 3 USED (low confidence) S. Shao, F. Akasheh, J. Wang, and Y. Liu, “Alternative misfit dislocations pattern in semi-coherent FCC 100 interfaces,” Acta Materialia. 2018. link Times cited: 26 USED (low confidence) X. Y. Chen et al., “Effect of dynamic evolution of misfit dislocation pattern on dislocation nucleation and shear sliding at semi-coherent bimetal interfaces,” Acta Materialia. 2018. link Times cited: 43 USED (low confidence) J. Li, Q. Fang, B. Liu, Y. Liu, and C. Jiang, “Twinning-governed plastic deformation in a thin film of body-centred cubic nanocrystalline ternary alloys at low temperature,” Journal of Alloys and Compounds. 2017. link Times cited: 22 USED (low confidence) A.Younes, N.Dilmi, M.Khorchef, A.Bouamer, N. Bacha, and M.Zergoug, “Structural and magnetic properties of FeCuNi nanostructured produced by mechanical alloying,” Applied Surface Science. 2017. link Times cited: 0 USED (low confidence) R. Jiang, A. Li, G. Cui, C. Zhang, H. Chen, and Y. Wang, “Influence of Ni-P content on microstructure and mechanical properties of Fe-x(Ni+P)-1Cu alloys,” Materials Science and Engineering A-structural Materials Properties Microstructure and Processing. 2017. link Times cited: 4 USED (low confidence) M. Kozłowski, D. Scopece, J. Janczak-Rusch, L. Jeurgens, R. Abdank-Kozubski, and D. Passerone, “Validation of an Embedded-Atom Copper Classical Potential via Bulk and Nanostructure Simulations,” Diffusion Foundations. 2017. link Times cited: 0 Abstract: The validation of classical potentials for describing multic… read moreAbstract: The validation of classical potentials for describing multicomponent materials in complex geometries and their high temperature structural modifications (disordering and melting) requires to verify both a faithful description of the individual phases and a convincing scheme for the mixed interactions, like it is the case of the embedded atom scheme. The present paper addresses the former task for an embedded atom potential for copper, namely the widely adopted parametrization by Zhou, through application to bulk, surface and nanocluster systems. It is found that the melting point is underestimated by 200 degrees with respect to experiment, but structural and temperature-dependent properties are otherwise faithfully reproduced. read less USED (low confidence) Y. Wang, J. Yin, X. Liu, R. Wang, H. Hou, and J. Wang, “Precipitation kinetics in binary Fe–Cu and ternary Fe–Cu–Ni alloys via kMC method,” Progress in Natural Science: Materials International. 2017. link Times cited: 15 USED (low confidence) K. Zolnikov, D. S. Kryzhevich, and A. Korchuganov, “Computer simulation of metal wire explosion under high rate heating,” Journal of Physics: Conference Series. 2017. link Times cited: 0 Abstract: Synchronous electric explosion of metal wires and synthesis … read moreAbstract: Synchronous electric explosion of metal wires and synthesis of bicomponent nanoparticles were investigated on the base of molecular dynamics method. Copper and nickel nanosized crystallites of cylindrical shape were chosen as conductors for explosion. The embedded atom approximation was used for calculation of the interatomic interactions. The agglomeration process after explosion metal wires was the main mechanism for particle synthesis. The distribution of chemical elements was non-uniform over the cross section of the bicomponent particles. The copper concentration in the surface region was higher than in the bulk of the synthesized particle. By varying the loading parameters (heating temperature, the distance between the wires) one can control the size and internal structure of the synthesized bicomponent nanoparticles. The obtained results showed that the method of molecular dynamics can be effectively used to determine the optimal technological mode of nanoparticle synthesis on the base of electric explosion of metal wires. read less USED (low confidence) G. Lv and Y. Su, “Molecular dynamics simulation and first principles calculations of radiation-induced Cu clusters in Fe-3 at.% Cu alloy,” Comput. Phys. Commun. 2017. link Times cited: 5 USED (low confidence) S. Fazeli, M. Vahedpour, and S. Sadrnezhaad, “What is the copper thin film thickness effect on thermal properties of NiTi/Cu bi-layer?,” Materials Research Express. 2017. link Times cited: 0 Abstract: Molecular dynamics (MD) simulation was used to study of ther… read moreAbstract: Molecular dynamics (MD) simulation was used to study of thermal properties of NiTi/Cu. Embedded atom method (EAM) potentials for describing of inter-atomic interaction and Nose–Hoover thermostat and barostat are employed. The melting of the bi-layers was considered by studying the temperature dependence of the cohesive energy and mean square displacement. To highlight the differences between bi-layers with various copper layer thickness, the effect of copper film thickness on thermal properties containing the cohesive energy, melting point, isobaric heat capacity and latent heat of fusion was estimated. The results show that thermal properties of bi-layer systems are higher than that of their corresponding of pure NiTi. But, these properties of bi-layer systems approximately are independent of copper film thicknesses. The mean square displacement (MSD) results show that, the diffusion coefficients enhance upon increasing of copper film thickness in a linear performance. read less USED (low confidence) S. Fazeli, M. Vahedpour, and S. Sadrnezhaad, “Comparison of the mechanical properties of NiTi/Cu bilayer by nanoindentation and tensile test: molecular dynamics simulation,” Materials Research Express. 2016. link Times cited: 5 Abstract: Molecular dynamics simulation was used to study of mechanica… read moreAbstract: Molecular dynamics simulation was used to study of mechanical properties of NiTi/Cu bilayer by nanoindentation and tensile testing. A comparison has been made among mechanical properties measured and plastic deformation process at different copper thickness during nanoindnetation and tensile test of the samples. Embedded atom method potentials for describing of inter-atomic interaction and Nose–Hoover thermostat and barostat are employed in the simulation at 400 K. The results showed that as the copper film thickness decreased, the maximum load and hardness values increased during nanoindetation. Saha and Nix model is used to describe reduced young’s modulus behaviour of the bilayer system through nanoindentation. A good agreement among calculated reduced elastic modulus by nanoindentation test and young’s modulus behaviour via tensile test have been obtained. The ‘incoherent interface’ in both of nanoindentation test and tensile testing is one of the governing factors for the dislocation propagation, which resulted in significant strengthening of the bilayer. It was observed that during tensile test, only copper layers were necked and fractured in all of samples. However, the present study seeks to examine the effect of film thickness on the free energy values that is obtained using Jarzynski’s equality during nanoindentation. As the copper film thickness was decreased, the free energy difference increased. According to both techniques, the thin film copper thickness provides lower number of nucleation locations resulting in the higher value of yield strength, hardness and free energy difference during nanoindenation. Mechanical properties of bilayer systems are improved with decreasing of copper film thickness. However, it specifies that strengths of all bilayer systems have prominent increase in young’s modulus in compared to the pure NiTi. read less USED (low confidence) K. Liu, R. Zhang, I. Beyerlein, X. Y. Chen, H. Yang, and T. Germann, “Cooperative dissociations of misfit dislocations at bimetal interfaces,” APL Materials. 2016. link Times cited: 18 Abstract: Using atomistic simulations, several semi-coherent cube-on-c… read moreAbstract: Using atomistic simulations, several semi-coherent cube-on-cube bimetal interfaces are comparatively investigated to unravel the combined effect of the character of misfit dislocations, the stacking fault energy difference between bimetal pairs, and their lattice mismatch on the dissociation of interfacial misfit dislocations. Different dissociation paths and features under loadings provide several unique deformation mechanisms that are critical for understanding interface strengthening. In particular, applied strains can cause either the formation of global interface coherency by the migration of misfit dislocations from an interface to an adjoining crystal interior or to an alternate packing of stacking faults connected by stair-rod dislocations. read less USED (low confidence) K. Zolnikov, D. S. Kryzhevich, and A. Korchuganov, “Features of particle synthesis at metal wire dispersion.” 2016. link Times cited: 0 Abstract: Features of particle synthesis under simultaneous dispersion… read moreAbstract: Features of particle synthesis under simultaneous dispersion of copper and nickel wires were investigated using a molecular dynamics method. The dynamics of wire dispersion, the size and phase composition of synthesized particles depend on the internal structure of dispersed metal wires and the distance between them. The main mechanism of particle synthesis was agglomeration of sputtered clusters, which predominated over the atom deposition from the gas phase on the particle surface. Synthesized particles were characterized by a nonuniform distribution of chemical elements along their cross section. The subsurface region had a higher concentration of copper in comparison with the particle volume. The molecular dynamics simulation of the metal wire dispersion allows finding optimal loading parameters for the synthesis of particles with desirable size and internal structure. read less USED (low confidence) J. Li, Q. Fang, B. Liu, and Y.-wen Liu, “The effects of pore and second-phase particle on the mechanical properties of machining copper matrix from molecular dynamic simulation,” Applied Surface Science. 2016. link Times cited: 28 USED (low confidence) D. H. Chung, H. Guk, S.-H. Choi, and D. Kim, “Wettability of Ag nanocluster on Cu-Ni alloys: A computational approach,” Journal of Alloys and Compounds. 2016. link Times cited: 5 USED (low confidence) C. Peng, K. Song, L. Wang, D. Şopu, S. Pauly, and J. Eckert, “Correlation between structural heterogeneity and plastic deformation for phase separating FeCu metallic glasses,” Scientific Reports. 2016. link Times cited: 8 USED (low confidence) D. Terentyev, A. Zinovev, and G. Bonny, “Displacement cascades in FeNiMnCu alloys: RVP model alloys,” Journal of Nuclear Materials. 2016. link Times cited: 7 USED (low confidence) L. You, L. Hu, Y. Xie, and S. Zhao, “Influence of Cu precipitation on tensile properties of Fe–Cu–Ni ternary alloy at different temperatures by molecular dynamics simulation,” Computational Materials Science. 2016. link Times cited: 14 USED (low confidence) A. Al-Motasem, N. Mai, S. Choi, and M. Posselt, “Atomistic study on mixed-mode fracture mechanisms of ferrite iron interacting with coherent copper and nickel nanoclusters,” Journal of Nuclear Materials. 2016. link Times cited: 10 USED (low confidence) A. Nikonov, I. Konovalenko, and A. Dmitriev, “Molecular dynamics study of lattice rearrangement under mechanically activated diffusion,” Physical Mesomechanics. 2016. link Times cited: 35 USED (low confidence) G. Lv, H. Zhang, X. He, W. Yang, and Y. Su, “Vacancy enhanced formation and phase transition of Cu-rich precipitates in α - iron under neutron irradiation,” AIP Advances. 2016. link Times cited: 2 Abstract: In this paper, we employed both molecular statics and molecu… read moreAbstract: In this paper, we employed both molecular statics and molecular dynamics simulation methods to investigate the role of vacancies in the formation and phase transition of Cu-rich precipitates in α-iron. The results indicated that vacancies promoted the diffusion of Cu atoms to form Cu-rich precipitates. After Cu-rich precipitates formed, they further trapped vacancies. The supersaturated vacancy concentration in the Cu-rich precipitate induced a shear strain, which triggered the phase transition from bcc to fcc structure by transforming the initial bcc (110) plane into fcc (111) plane. In addition, the formation of the fcc-twin structure and the stacking fault structure in the Cu-rich precipitates was observed in dynamics simulations. read less USED (low confidence) C. Liu, Z. Jiao, and J. Luan, “Copper-Rich Nanoclusters: Ferritic Steels Strengthened.” 2016. link Times cited: 3 USED (low confidence) A. Nikonov, I. Konovalenko, and A. Dmitriev, “Molecular dynamics study of lattice rearrangement under mechanically activated diffusion,” Physical Mesomechanics. 2016. link Times cited: 0 USED (low confidence) S. Shao, J. Wang, I. Beyerlein, and A. Misra, “Glide dislocation nucleation from dislocation nodes at semi-coherent 1 1 1 Cu–Ni interfaces,” Acta Materialia. 2015. link Times cited: 82 USED (low confidence) F. Z. Dai and W.-Z. Zhang, “An automatic and simple method for specifying dislocation features in atomistic simulations,” Comput. Phys. Commun. 2015. link Times cited: 26 USED (low confidence) F. Akasheh, M. R. Karim, and S. Shao, “Dislocation Structure of Cu/Nu (100) Semi-Coherent Interface and Its Role in Lattice Dislocation Nucleation.” 2015. link Times cited: 1 USED (low confidence) D. Terentyev, X. He, G. Bonny, A. Bakaev, E. Zhurkin, and L. Malerba, “Hardening due to dislocation loop damage in RPV model alloys: Role of Mn segregation,” Journal of Nuclear Materials. 2015. link Times cited: 36 USED (low confidence) Y. Qi, L. Wang, S. Wang, X. Li, and W. Cui, “Structural and dynamical heterogeneity of undercooled Fe75Cu25 melts with miscibility gap,” Journal of Alloys and Compounds. 2014. link Times cited: 11 USED (low confidence) C. Hu, M.-li Bai, J. Lv, H. Liu, and X.-jie Li, “Molecular dynamics investigation of the effect of copper nanoparticle on the solid contact between friction surfaces,” Applied Surface Science. 2014. link Times cited: 47 USED (low confidence) F. Bergner, A. Ulbricht, P. Lindner, U. Keiderling, and L. Malerba, “Post-irradiation annealing behavior of neutron-irradiated FeCu, FeMnNi and FeMnNiCu model alloys investigated by means of small-angle neutron scattering,” Journal of Nuclear Materials. 2014. link Times cited: 11 USED (low confidence) G. Bonny, D. Terentyev, E. Zhurkin, and L. Malerba, “Monte Carlo study of decorated dislocation loops in FeNiMnCu model alloys,” Journal of Nuclear Materials. 2014. link Times cited: 45 USED (low confidence) H. Morita and A. Takahashi, “Numerical analysis of interaction between solute atom and extended dislocation using force multipoles,” Journal of Central South University. 2014. link Times cited: 0 USED (low confidence) S. Shao, J. Wang, A. Misra, and R. Hoagland, “Relaxation of Misfit Dislocations at Nodes,” Materials Science Forum. 2014. link Times cited: 3 Abstract: Experimental studies proved that structures and properties o… read moreAbstract: Experimental studies proved that structures and properties of misfit dislocations and their intersections (nodes) in semi-coherent interfaces strongly affect thermal and mechanical stability of interface. Employing atomistic simulations, we reveal that misfit dislocation lines can exhibit a spiral pattern (SP) or remain straight in association with dislocation character at nodes. By analyzing nodes formation processes in terms of kinetics and energetics, we found that the variation is ascribed to the competition between core energy of misfit dislocation and interface stacking fault energy with respect to coherent interface. read less USED (low confidence) B. Onat and S. Durukanoğlu, “An optimized interatomic potential for Cu–Ni alloys with the embedded-atom method,” Journal of Physics: Condensed Matter. 2014. link Times cited: 86 Abstract: We have developed a semi-empirical and many-body type model … read moreAbstract: We have developed a semi-empirical and many-body type model potential using a modified charge density profile for Cu–Ni alloys based on the embedded-atom method (EAM) formalism with an improved optimization technique. The potential is determined by fitting to experimental and first-principles data for Cu, Ni and Cu–Ni binary compounds, such as lattice constants, cohesive energies, bulk modulus, elastic constants, diatomic bond lengths and bond energies. The generated potentials were tested by computing a variety of properties of pure elements and the alloy of Cu, Ni: the melting points, alloy mixing enthalpy, lattice specific heat, equilibrium lattice structures, vacancy formation and interstitial formation energies, and various diffusion barriers on the (100) and (111) surfaces of Cu and Ni. read less USED (low confidence) G. Bonny et al., “On the thermal stability of late blooming phases in reactor pressure vessel steels: An atomistic study,” Journal of Nuclear Materials. 2013. link Times cited: 77 USED (low confidence) Z. Jiao, J. Luan, Z. Zhang, M. K. Miller, W. Ma, and C. Liu, “Synergistic effects of Cu and Ni on nanoscale precipitation and mechanical properties of high-strength steels,” Acta Materialia. 2013. link Times cited: 163 USED (low confidence) X. Shu et al., “Fe self-diffusion and Cu and Ni diffusion in bulk and grain boundary of Fe: A molecular dynamics study,” Nuclear Instruments & Methods in Physics Research Section B-beam Interactions With Materials and Atoms. 2013. link Times cited: 10 USED (low confidence) L. Shao et al., “Smoothing metallic glasses without introducing crystallization by gas cluster ion beam,” Applied Physics Letters. 2013. link Times cited: 13 Abstract: We show that 30 keV Ar cluster ion bombardment of Ni52.5Nb10… read moreAbstract: We show that 30 keV Ar cluster ion bombardment of Ni52.5Nb10Zr15Ti15Pt7.5 metallic glass (MG) can remove surface mountain-like features and reduce the root mean square surface roughness from 12 nm to 0.7 nm. X-ray diffraction analysis reveals no crystallization after cluster ion irradiation. Molecular dynamics simulations show that, although damage cascades lead to local melting, the subsequent quenching rate is a few orders of magnitude higher than the critical cooling rate for MG formation, thus the melted zone retains its amorphous nature down to room temperature. These findings can be applied to obtain ultra-smooth MGs without introducing crystallization. read less USED (low confidence) Y. Shim, N. Callahan, and J. Amar, “Localized saddle-point search and application to temperature-accelerated dynamics.,” The Journal of chemical physics. 2013. link Times cited: 9 Abstract: We present a method for speeding up temperature-accelerated … read moreAbstract: We present a method for speeding up temperature-accelerated dynamics (TAD) simulations by carrying out a localized saddle-point (LSAD) search. In this method, instead of using the entire system to determine the energy barriers of activated processes, the calculation is localized by only including a small chunk of atoms around the atoms directly involved in the transition. Using this method, we have obtained N-independent scaling for the computational cost of the saddle-point search as a function of system size N. The error arising from localization is analyzed using a variety of model systems, including a variety of activated processes on Ag(100) and Cu(100) surfaces, as well as multiatom moves in Cu radiation damage and metal heteroepitaxial growth. Our results show significantly improved performance of TAD with the LSAD method, for the case of Ag/Ag(100) annealing and Cu/Cu(100) growth, while maintaining a negligibly small error in energy barriers. read less USED (low confidence) D. Molnár et al., “Multiscale simulations on the coarsening of Cu-rich precipitates in α-Fe using kinetic Monte Carlo, molecular dynamics and phase-field simulations,” Acta Materialia. 2012. link Times cited: 59 USED (low confidence) N. Gunkelmann, H. Ledbetter, and H. Urbassek, “Experimental and atomistic study of the elastic properties of α′ Fe–C martensite,” Acta Materialia. 2012. link Times cited: 38 USED (low confidence) D. Terentyev and L. Malerba, “Interaction of a screw dislocation with Cu-precipitates, nanovoids and Cu–vacancy clusters in BCC iron,” Journal of Nuclear Materials. 2012. link Times cited: 34 USED (low confidence) Y. Ashkenazy, N. Q. Vo, D. Schwen, R. Averback, and P. Bellon, “Shear induced chemical mixing in heterogeneous systems,” Acta Materialia. 2012. link Times cited: 108 USED (low confidence) D. Terentyev, L. Malerba, G. Bonny, A. Al-Motasem, and M. Posselt, “Interaction of an edge dislocation with Cu–Ni-vacancy clusters in bcc iron,” Journal of Nuclear Materials. 2011. link Times cited: 24 USED (low confidence) A. Al-Motasem, M. Posselt, and F. Bergner, “Nanoclusters in bcc-Fe containing vacancies, copper and nickel: Structure and energetics,” Journal of Nuclear Materials. 2011. link Times cited: 25 USED (low confidence) B. Jelinek et al., “Modified embedded atom method potential for Al, Si, Mg, Cu, and Fe alloys,” Physical Review B. 2011. link Times cited: 218 Abstract: A set of modified embedded-atom method (MEAM) potentials for… read moreAbstract: A set of modified embedded-atom method (MEAM) potentials for the interactions between Al, Si, Mg, Cu, and Fe was developed from a combination of each element's MEAM potential in order to study metal alloying. Previously published MEAM parameters of single elements have been improved for better agreement to the generalized stacking fault energy (GSFE) curves when compared with ab initio generated GSFE curves. The MEAM parameters for element pairs were constructed based on the structural and elastic properties of element pairs in the NaCl reference structure garnered from ab initio calculations, with adjustment to reproduce the ab initio heat of formation of the most stable binary compounds. The new MEAM potentials were validated by comparing the formation energies of defects, equilibrium volumes, elastic moduli, and heat of formation for several binary compounds with ab initio simulations and experiments. Single elements in their ground-state crystal structure were subjected to heating to test the potentials at elevated temperatures. An Al potential was modified to avoid formation of an unphysical solid structure at high temperatures. The thermal expansion coefficient of a compound with the composition of AA 6061 alloy was evaluated and compared with experimental values. MEAM potential tests performed in this work, utilizing the universal atomistic simulation environment (ASE), are distributed to facilitate reproducibility of the results. read less USED (low confidence) L. Malerba et al., “Comparison of empirical interatomic potentials for iron applied to radiation damage studies,” Journal of Nuclear Materials. 2010. link Times cited: 210 USED (low confidence) N. Castin, L. Malerba, G. Bonny, M. I. Pascuet, and M. Hou, “Modelling radiation-induced phase changes in binary FeCu and ternary FeCuNi alloys using an artificial intelligence-based atomistic kinetic Monte Carlo approach,” Nuclear Instruments & Methods in Physics Research Section B-beam Interactions With Materials and Atoms. 2009. link Times cited: 24 USED (low confidence) K. Chen et al., “Extra-ductile and strong tin bronze alloy via high-density intragranular ultra-nano precipitation with minimal lattice misfit,” Scripta Materialia. 2023. link Times cited: 0 USED (low confidence) F. Wang et al., “Atomic-scale simulations in multi-component alloys and compounds: A review on advances in interatomic potential,” Journal of Materials Science & Technology. 2023. link Times cited: 9 USED (low confidence) A. Nikonov and A. I. Dmitriev, “Molecular-dynamic calculation of the interaction parameters of meso-scale particles of dissimilar metals,” PHYSICAL MESOMECHANICS OF CONDENSED MATTER: Physical Principles of Multiscale Structure Formation and the Mechanisms of Nonlinear Behavior: MESO2022. 2023. link Times cited: 0 USED (low confidence) S. Eder, P. Grützmacher, M. R. Ripoll, C. Gachot, and D. Dini, “Does speed kill or make friction better?—Designing materials for high velocity sliding,” Applied Materials Today. 2022. link Times cited: 7 USED (low confidence) D. Mejía-Burgos, S. Berrios, J. Mazo‐Zuluaga, and J. Mejía‐López, “Structural stability, shape memory and mechanical properties of Fe/Ni core/shell nanorods,” Journal of Alloys and Compounds. 2021. link Times cited: 0 USED (low confidence) L. Malerba, “Large Scale Integrated Materials Modeling Programs.” 2020. link Times cited: 2 USED (low confidence) C. Becquart and F. Soisson, “Monte Carlo Simulations of Precipitation Under Irradiation,” Handbook of Mechanics of Materials. 2019. link Times cited: 7 USED (low confidence) D. Rapp et al., “Multiscale Simulation of Precipitation in Copper-Alloyed Pipeline Steels and in Cu-Ni-Si Alloys,” Handbook of Mechanics of Materials. 2019. link Times cited: 0 USED (low confidence) Ž. Božić, S. Schmauder, M. Mlikota, and M. Hummel, “Multiscale Fatigue Crack Growth Modeling for Welded Stiffened Panels,” Handbook of Mechanics of Materials. 2019. link Times cited: 3 USED (low confidence) S. Fazeli, M. Vahedpour, and S. Sadrnezhaad, “Effect of copper content on tensile mechanical properties of ternary NiTiCu alloy nanowire: Molecular dynamics simulation,” Materials Today: Proceedings. 2018. link Times cited: 4 USED (low confidence) K. Zolnikov, D. S. Kryzhevich, and A. Korchuganov, “Peculiarities of structural transformations in metal nanoparticles at high speed collisions,” Journal of Physics: Conference Series. 2018. link Times cited: 1 Abstract: A molecular dynamics simulation of nanosized particle collis… read moreAbstract: A molecular dynamics simulation of nanosized particle collision under the electrical explosion of metal wires of different types was conducted. Interatomic interactions were described on the base of the embedded atom method. Used potentials allowed describing with high accuracy many mechanical and physical properties which are very important for the simulations of nanoparticle collisions with high velocities. The dynamics of the nanosized particle formation at the electric pulse explosion of metal wires of different types was studied. Features of particle collisions on the example of nanoscale particles of copper and nickel, whose velocities varied from 50 to 1500 m/s were investigated. The peculiarities of structural transformations in the colliding particles depending on the velocity of collision were determined. The intervals of collision velocities in which interaction between particles is elastic or leads to the formation of structural defects or melting were calculated. The analysis of the structure and distribution of chemical elements over the cross section of the particles which were synthesized under simultaneous explosions of different metal wires was carried out. read less USED (low confidence) K. Zolnikov, D. Kryzhevich, E. Shilko, and A. Korchuganov, “Molecular Dynamics Simulation Of Electric Pulse Explosion Of Metal Wires,” Procedia structural integrity. 2016. link Times cited: 1 USED (low confidence) M. Hummel, A.-P. Prskalo, P. Binkele, and S. Schmauder, “MD-Simulations on Metallic Alloys,” International Conference on High Performance Computing. 2015. link Times cited: 1 USED (low confidence) D. Molnár, P. Binkele, A. Mora, R. Mukherjee, B. Nestler, and S. Schmauder, “Molecular Dynamics virtual testing of thermally aged Fe–Cu microstructures obtained from multiscale simulations,” Computational Materials Science. 2014. link Times cited: 9 USED (low confidence) I. Mastorakos, H. Zbib, D. Li, M. Khaleel, and X. Sun, “Multiscale Modeling of Irradiation Induced Hardening in Iron Alloys,” MRS Proceedings. 2012. link Times cited: 0 USED (low confidence) E. Lin, L. Niu, H.-ji Shi, and Z. Duan, “Molecular dynamics simulation of nano-scale interfacial friction characteristic for different tribopair systems,” Applied Surface Science. 2012. link Times cited: 26 USED (low confidence) L. Malerba, “Multi-scale modelling of irradiation effects in nuclear power plant materials.” 2010. link Times cited: 3 Abstract: Abstract: This chapter surveys the computer-based multi-scal… read moreAbstract: Abstract: This chapter surveys the computer-based multi-scale modelling approaches currently being used to develop physical models of the effects of radiation on nuclear materials. The focus is on the problem of radiation-induced hardening (and embrittlement) in steels, limited to the scales ranging from the nucleus to the single crystal. First, the multi-scale nature of radiation effects is illustrated, including examples of microstructural and mechanical property changes observed in steels used in nuclear reactors. Then the chapter discusses the fundamental ideas upon which the multi-scale modelling approach is based. Next, an overview of the techniques of use in a multi-scale modelling framework is given, with an example of how these can be integrated. A discussion of the state-of-the-art and other general remarks conclude the chapter. read less NOT USED (high confidence) G. Chu et al., “MD Simulation of Hundred-Billion-Metal-Atom Cascade Collision on Sunway Taihulight,” Comput. Phys. Commun. 2021. link Times cited: 7 NOT USED (high confidence) P. Yu, L. Zhang, and L. Du, “Atomic Simulations for Packing Changes of Nano-Sized Cu Clusters Embedded in the Febulk on Heating,” Metals. 2021. link Times cited: 3 Abstract: Understanding of the defect evolution mechanism under irradi… read moreAbstract: Understanding of the defect evolution mechanism under irradiation is very important for the research of pressure vessel steel embrittlement. In this paper, the embedded atom method (EAM) based canonical ensemble molecular dynamics (MD) method was used to study the evolution of the stacking structure of different nano-sized Cun (n = 13, 43 and 87) clusters in an Febulk embedded with BCC lattice structure during continuous heating. The mean square displacement, pair distribution functions and atomic structures of Cu atom clusters at the nanometer scale were calculated at different temperatures. The structural changes present apparent differences, for the Febulks contain nano-sized Cu clusters with different atom numbers during heating. For the Febulk–Cu13 system, since the ability to accommodate the atomic Cu in the Fe substrate is lesser, a small number of Cu atoms in BCC lattice positions cannot influence the whole structure of the Fe-Cu system. For the Febulk–Cu43 system, with an increase in temperature, a Cu atomic pile structural change happened, and the strain areas decreased significantly in the Febulk, but a single strain area grew large. For the Febulk–Cu87 system, when the Cu atoms are constrained by the Fe atoms in bulk, only a few of the Cu atoms adjust their positions. With the increase in temperature, strain in the Fe eased. read less NOT USED (high confidence) B. Lin, J. Wang, J. Li, and Z. Wang, “A neural-network based framework of developing cross interaction in alloy embedded-atom method potentials: application to Zr–Nb alloy,” Journal of Physics: Condensed Matter. 2020. link Times cited: 2 Abstract: Interaction potentials are critical to molecular dynamics si… read moreAbstract: Interaction potentials are critical to molecular dynamics simulations on fundamental mechanisms at atomic scales. Combination of well-developed single-element empirical potentials via cross interaction (CI) is an important and effective way to develop alloy embedded-atom method (EAM) potentials. In this work, based on neural-network (NN) models, firstly we proposed a framework to construct CI potential functions via utilizing single-element potentials. The framework contained four steps: (1) extracting characteristic points from single-element potential functions, (2) constructing CI functions by cubic spline interpolation, (3) evaluating the accuracy of CI functions by referring to first-principle (FP) data, and (4) searching for reasonable CI functions via NN models. Then with this framework, we developed a Zr–Nb alloy CI potential utilizing the MA-III (pure Zr potential developed by Mendelev and Ackland in 2007) and the Fellinger, Park and Wilkins (FPW) (pure Nb potential developed by FPW in 2010) potentials as single-element parts. The calculated results with this Zr–Nb alloy potential showed that: (1) the newly developed CI potential functions could simultaneously present the potential-function features of Zr and Nb; (2) the normalized energy–volume curves of L12 Zr3Nb, B2 ZrNb and L12 ZrNb3 calculated by this CI potential reasonably agreed with FP results; (3) the referred MA-III Zr and FPW Nb potentials can satisfactorily reproduce the priority of prismatic slip in Zr and the tension–compression asymmetry of 〈111〉{112} slip in Nb, while other ab initio developed Zr–Nb alloy potentials cannot. Our study indicates that, this NN based framework can take full advantage of single-element potentials, and is very convenient to develop EAM potentials of alloys; moreover, the new-developed Zr–Nb alloy EAM potential can reasonably describe the complicated deformation behaviors in Zr–Nb systems. read less NOT USED (high confidence) S. Eder, M. R. Ripoll, U. Cihak-Bayr, D. Dini, and C. Gachot, “Unraveling and Mapping the Mechanisms for Near-surface Microstructure Evolution in CuNi Alloys under Sliding.,” ACS applied materials & interfaces. 2020. link Times cited: 30 Abstract: The origin of friction and wear in polycrystalline materials… read moreAbstract: The origin of friction and wear in polycrystalline materials is intimately connected with their microstructural response to interfacial stresses. Although many mechanisms that govern microstructure evolution in sliding contacts are generally understood, it is still a challenge to ascertain which mechanisms matter under what conditions, which limits the development of tailor-made microstructures for reducing friction and wear. Here, we shed light on the circumstances that promote plastic deformation and surface damage by studying several FCC CuNi alloys subjected to sliding with molecular dynamics simulations featuring tens of millions of atoms. By analyzing the depth- and time-dependent evolution of the grain size, twinning, shear, and the stresses in the aggregate, we derive a deformation mechanism map for CuNi alloys. We verify the predictions of this map against focused ion beam images of the near-surface regions of CuNi alloys that were experimentally subjected to similar loading conditions. Our results may serve as a tool for finding optimum material compositions within a specified operating range. read less NOT USED (high confidence) T. M. Whiting, P. Burr, D. King, and M. Wenman, “Understanding the importance of the energetics of Mn, Ni, Cu, Si and vacancy triplet clusters in bcc Fe,” Journal of Applied Physics. 2019. link Times cited: 11 Abstract: Numerous experimental studies have found the presence of (Cu… read moreAbstract: Numerous experimental studies have found the presence of (Cu)-Ni-Mn-Si clusters in neutron irradiated reactor pressure vessel steels, prompting concerns that these clusters could lead to larger than expected increases in hardening, especially at high fluences late in life. The mechanics governing clustering for the Fe-Mn-Ni-Si system are not well-known; state-of-the-art methods use kinetic Monte Carlo (KMC) parameterized by density functional theory (DFT) and thermodynamic data to model the time evolution of clusters. However, DFT-based KMC studies have so far been limited to only pairwise interactions due to lack of DFT data. Here, we explicitly calculate the binding energy of triplet clusters of Mn, Ni, Cu, Si, and vacancies in bcc Fe using DFT to show that the presence of vacancies, Si, or Cu stabilizes cluster formation, as clusters containing exclusively Mn and/or Ni are not energetically stable in the absence of interstitials. We further identify which clusters may be reasonably approximated as a sum of pairwise interactions and which instead require an explicit treatment of the three-body interaction, showing that the three-body term can account for as much as 0.3 eV, especially for clusters containing vacancies. read less NOT USED (high confidence) S. Zhi-peng, D. Fuzhi, X. Ben, and Z. Wen-zheng, “Three-Dimensional Growth of Coherent Ferrite in Austenite: A Molecular Dynamics Study,” Acta Metallurgica Sinica (english Letters). 2019. link Times cited: 1 NOT USED (high confidence) X. Wu et al., “Softening effects due to reorientations of Cu precipitates in α-iron: Atomistic simulations of dislocations-obstacles interactions,” Journal of Applied Physics. 2019. link Times cited: 3 Abstract: Radiation-induced hardening by precipitates, which essential… read moreAbstract: Radiation-induced hardening by precipitates, which essentially has a dislocation pinning effect, is a major issue in nuclear reactor pressure vessels research. In this study, simulations of interactions between edge dislocations and copper precipitates are conducted as an example to investigate size-dependent pinning effects. Using molecular dynamics simulations, we discover a new two-stage mechanism that includes the processes of reorientations and atomistic collective migrations during the interactions. Both of these result in a weakening of the pinning effect on dislocations when the phase transition occurs in copper precipitates, which can be reflected in the decrease of the critical shear stress in stress and strain curves. Our studies considered the atomistic arrangement of the obstacle during the interaction, which constructively provide a new perspective for research studies of dislocation–obstacle pinning interaction and offer a more comprehensive estimation on the pinning strength of dislocations.Radiation-induced hardening by precipitates, which essentially has a dislocation pinning effect, is a major issue in nuclear reactor pressure vessels research. In this study, simulations of interactions between edge dislocations and copper precipitates are conducted as an example to investigate size-dependent pinning effects. Using molecular dynamics simulations, we discover a new two-stage mechanism that includes the processes of reorientations and atomistic collective migrations during the interactions. Both of these result in a weakening of the pinning effect on dislocations when the phase transition occurs in copper precipitates, which can be reflected in the decrease of the critical shear stress in stress and strain curves. Our studies considered the atomistic arrangement of the obstacle during the interaction, which constructively provide a new perspective for research studies of dislocation–obstacle pinning interaction and offer a more comprehensive estimation on the pinning strength of dislocations. read less NOT USED (high confidence) C. Hu, J. Lv, M.-li Bai, X. Zhang, and D. Tang, “Molecular dynamics simulation of effects of nanoparticles on frictional heating and tribological properties at various temperatures,” Friction. 2019. link Times cited: 26 NOT USED (high confidence) Z. Sun, F. Z. Dai, B. Xu, and W.-Z. Zhang, “Three-Dimensional Growth of Coherent Ferrite in Austenite: A Molecular Dynamics Study,” Acta Metallurgica Sinica (English Letters). 2019. link Times cited: 5 NOT USED (high confidence) S. Mahmoud and N. Mousseau, “Long-time point defect diffusion in ordered nickel-based binary alloys: How small kinetic differences can lead to completely long-time structural evolution,” Materialia. 2018. link Times cited: 15 NOT USED (high confidence) Y. Zhang, D. Schwen, and X. Bai, “Molecular dynamics simulations of concentration-dependent defect production in Fe-Cr and Fe-Cu alloys,” Journal of Applied Physics. 2017. link Times cited: 13 Abstract: Molecular dynamics simulations are conducted to study the ef… read moreAbstract: Molecular dynamics simulations are conducted to study the effects of alloying elements on the primary damage behaviors in three Fe-based ferritic alloy systems: (1) a Fe-Cr system in which the heat of mixing changes its sign with the Cr concentration; (2) a Fe-Cu system that has a positive heat of mixing; and (3) an ideal but artificial Fe-Cr system that has a zero heat of mixing, which is used as a reference system to investigate solute interstitial formation based on probability. It is found that in these alloys, the solute type and concentration do not have a significant effect on the total number of surviving Frenkel pairs. However, the fraction of solute interstitials has distinct behaviors. In Fe-Cr, the Cr interstitial fraction is much higher than the Cr solute concentration and the Cr interstitial production efficiency decreases with the increasing Cr concentration. By contrast, in Fe-Cu, Cu interstitials are barely produced. In the ideal alloy, the solute interstitial fraction is close to the sol... read less NOT USED (high confidence) B. Cheng and M. Ceriotti, “Computing the absolute Gibbs free energy in atomistic simulations: Applications to defects in solids,” Physical Review B. 2017. link Times cited: 40 Abstract: The Gibbs free energy is the fundamental thermodynamic poten… read moreAbstract: The Gibbs free energy is the fundamental thermodynamic potential underlying the relative stability of different states of matter under constant-pressure conditions. However, computing this quantity from atomic-scale simulations is far from trivial. As a consequence, all too often the potential energy of the system is used as a proxy, overlooking entropic and anharmonic effects. Here we discuss a combination of different thermodynamic integration routes to obtain the absolute Gibbs free energy of a solid system starting from a harmonic reference state. This approach enables the direct comparison between the free energy of different structures, circumventing the need to sample the transition paths between them. We showcase this thermodynamic integration scheme by computing the Gibbs free energy associated with a vacancy in BCC iron, and the intrinsic stacking fault free energy of nickel. These examples highlight the pitfalls of estimating the free energy of crystallographic defects only using the minimum potential energy, which overestimates the vacancy free energy by 60% and the stacking-fault energy by almost 300% at temperatures close to the melting point. read less NOT USED (high confidence) K. Liu et al., “Effect of Ni and vacancy concentration on initial formation of Cu precipitate in Fe–Cu–Ni ternary alloys by molecular dynamics simulation,” Chinese Physics B. 2017. link Times cited: 5 NOT USED (high confidence) A. Akbarzadeh, Y. Cui, and Z. Chen, “Thermal wave: from nonlocal continuum to molecular dynamics,” RSC Advances. 2017. link Times cited: 24 Abstract: It is well known that the continuum model of Fourier's … read moreAbstract: It is well known that the continuum model of Fourier's law of heat conduction violates the relativity theory, admits an instantaneous thermal response, and assumes a quasi-equilibrium thermodynamic condition. Transient heat transport, however, is a non-equilibrium phenomenon with a finite thermal wave speed for applications involving very low temperatures, extremely high temperature gradients, and ballistic heat transfers. Hyperbolic and phase-lag heat conduction models have enabled detection of the finite thermal wave speed in heat transport. To accommodate effects of thermomass and size-dependency of thermophysical properties on nano/microscale heat transport and to remove the theoretical singularity of temperature gradients across the thermal wavefront, a nonlocal, fractional-order, three-phase-lag heat conduction is introduced. The model is capable of simulating heat conduction phenomena in multiple spatio-temporal scales. To confirm the existence of thermal waves in nano/microscale heat transport, a molecular dynamics simulation is implemented for the heat transfer within a nanoscale copper slab. Correlating thermal responses in continuum and atomistic scales sheds light on the effect of length scale, fractional order, and phase-lags in multiscale heat transport. The multiscale simulation is of practical importance for microelectromechanical system design, photothermal techniques, and ultrafast laser-assisted processing of advanced materials. read less NOT USED (high confidence) S. M. Rassoulinejad-Mousavi, Y. Mao, and Y. Zhang, “Evaluation of Copper, Aluminum and Nickel Interatomic Potentials on Predicting the Elastic Properties,” arXiv: Computational Physics. 2016. link Times cited: 63 Abstract: Choice of appropriate force field is one of the main concern… read moreAbstract: Choice of appropriate force field is one of the main concerns of any atomistic simulation that needs to be seriously considered in order to yield reliable results. Since, investigations on mechanical behavior of materials at micro/nanoscale has been becoming much more widespread, it is necessary to determine an adequate potential which accurately models the interaction of the atoms for desired applications. In this framework, reliability of multiple embedded atom method based interatomic potentials for predicting the elastic properties was investigated. Assessments were carried out for different copper, aluminum and nickel interatomic potentials at room temperature which is considered as the most applicable case. Examined force fields for the three species were taken from online repositories of National Institute of Standards and Technology (NIST), as well as the Sandia National Laboratories, the LAMMPS database. Using molecular dynamic simulations, the three independent elastic constants, C11, C12 and C44 were found for Cu, Al and Ni cubic single crystals. Voigt-Reuss-Hill approximation was then implemented to convert elastic constants of the single crystals into isotropic polycrystalline elastic moduli including Bulk, Shear and Young's modulus as well as Poisson's ratio. Simulation results from massive molecular dynamic were compared with available experimental data in the literature to justify the robustness of each potential for each species. Eventually, accurate interatomic potentials have been recommended for finding each of the elastic properties of the pure species. Exactitude of the elastic properties was found to be sensitive to the choice of the force fields. Those potentials were fitted for a specific compound may not necessarily work accurately for all the existing pure species. read less NOT USED (high confidence) I. Hijazi and Y. H. Park, “Mixed intermetallic potentials for Fe-Cu compounds,” Molecular Simulation. 2016. link Times cited: 0 Abstract: Metastable Fe-Cu alloys are of considerable scientific inter… read moreAbstract: Metastable Fe-Cu alloys are of considerable scientific interest, and an efficient interatomic potential is crucial for reliable atomistic simulations. Interatomic potentials developed for pure Fe and pure Cu are difficult to mix for the Fe-Cu alloys since the analytic function form of pure Fe is not of the same type of pure Cu potential. Additionally, elemental potentials taken from alloy descriptions may not work well for the pure species. This is particularly true if the elements were fit for compounds instead of being optimised separately. In this article, we present compatible analytic function forms that work for pure species and are easily mixed with two adjustable parameters for their alloys. We tested the proposed potentials to make sure that the performance is adequate for pure species as well as their alloys. The predicted values were in good agreement with experimental results. read less NOT USED (high confidence) S. Parviainen, F. Djurabekova, S. Fitzgerald, A. Ruzibaev, and K. Nordlund, “Atomistic simulations of field assisted evaporation in atom probe tomography,” Journal of Physics D: Applied Physics. 2016. link Times cited: 19 Abstract: Atom probe tomography (APT) is an extremely powerful techniq… read moreAbstract: Atom probe tomography (APT) is an extremely powerful technique for determining the three-dimensional structure and chemical composition of a given sample. Although it is designed to provide images of material structure with atomic scale resolution, reconstruction artifacts, well-known to be present in reconstructed images, reduce their accuracy. No existing simulation technique has been able to describe the origin of these artifacts. Here we develop a simulation technique which allows for atomistic simulations of the atom emission process in the presence of high electric fields in APT experiments. Our code combines hybrid concurrent electrodynamics—molecular dynamics and a Monte Carlo approach. We use this technique to demonstrate the atom-level origin of artifacts in APT image reconstructions on examples of inclusions and voids in investigated samples. The results show that even small variations in the surface topology give rise to distortions in the local electric field, limiting the accuracy of conventional APT reconstruction algorithms. read less NOT USED (high confidence) C. Hu, M.-li Bai, J. Lv, Z. Kou, and X.-jie Li, “Molecular dynamics simulation on the tribology properties of two hard nanoparticles (diamond and silicon dioxide) confined by two iron blocks,” Tribology International. 2015. link Times cited: 46 NOT USED (high confidence) Z. Lu-shan and Z. Shi-jin, “Influence of Ni on Cu precipitation in Fe—Cu—Ni ternary alloy by an atomic study,” Chinese Physics B. 2014. link Times cited: 9 Abstract: The early aging Cu precipitations in Fe—3%Cu and Fe—3%Cu—4%N… read moreAbstract: The early aging Cu precipitations in Fe—3%Cu and Fe—3%Cu—4%Ni ternary alloys are investigated by molecular dynamics (MD) simulations. The results show that the average size of Cu clusters in Fe—3%Cu—4%Ni alloy is larger than that in Fe—3%Cu alloy. The diffusion of Cu is accelerated by Ni according to the mean square displacement (MSD). Furthermore, the whole formation process of Cu-rich clusters is analyzed in detail, and it is found that the presence of Ni promotes small Cu-rich clusters to be combined into big ones. Ni atoms prefer to stay at the combination positions of small clusters energetically due to a large number of the first nearest neighbor Cu—Ni interactions, which is verified by first-principles calculations based on density functional theory (DFT). read less NOT USED (high confidence) W. Song and S.-jin Zhao, “Spin polarization gives rise to Cu precipitation in Fe-matrix.,” Physical chemistry chemical physics : PCCP. 2014. link Times cited: 9 Abstract: This article tries to uncover the physical reason of Cu prec… read moreAbstract: This article tries to uncover the physical reason of Cu precipitation from an Fe matrix at the electronic level. The general rule is obtained that the more bonds among Cu atoms, the more stable the system is. It was shown that Cu would precipitate from the matrix with Fe spin-polarization but not without spin-polarization. The partial density of states (PDOS) analysis illustrated that the d states of Fe near the Fermi level potentially have strong interaction with other atoms, but Cu d states below the Fermi level lack this potential, which results in weak covalent d orbital interaction between Fe and Cu. Furthermore, the charge density difference also confirmed the weaker bond between Fe and Cu with spin-polarization compared to without spin-polarization, due to the decreased charge between them. In addition, the {110} interface energy between Fe and Cu, estimated by the "dangling bond", is 676.3 mJ m(-2), which agrees with the DFT calculation, 414.2 mJ m(-2). Finally, this study also revealed that Ni atoms can reduce the "dangling bond" when it locates at the interface and separates Fe and Cu. read less NOT USED (high confidence) J. Amar, Y. Shim, and R. Deck, “Critical island size for a shape transition in strained Cu/Ni(100) islands,” Surface Science. 2013. link Times cited: 3 NOT USED (high confidence) Q.-dong Liu, J. Gu, and W.-qing Liu, “On the Role of Ni in Cu Precipitation in Multicomponent Steels,” Metallurgical and Materials Transactions A. 2013. link Times cited: 19 NOT USED (high confidence) Y. Shim and J. Amar, “Shape transitions in strained Cu islands on Ni(100): kinetics versus energetics.,” Physical review letters. 2012. link Times cited: 7 Abstract: We examine the ramified islands observed in submonolayer Cu/… read moreAbstract: We examine the ramified islands observed in submonolayer Cu/Ni(100) growth. Our results indicate that the strain-energy contribution to the dependence of island energy on shape is surprisingly weak. In contrast, our accelerated dynamics simulations indicate that unexpected concerted popout processes occurring at step edges may be responsible. Kinetic Monte Carlo (KMC) simulations which include these processes produce island shapes which are very similar to those observed in experiment. These results suggest that the shape transition is of kinetic origin but is strongly mediated by strain. read less NOT USED (high confidence) L. Malerba et al., “Ab initio calculations and interatomic potentials for iron and iron alloys : Achievements within the Perfect Project,” Journal of Nuclear Materials. 2010. link Times cited: 65 NOT USED (high confidence) G. Bonny and R. Pasianot, “Gauge transformations to combine multi-component many-body interatomic potentials,” Philosophical Magazine Letters. 2010. link Times cited: 19 Abstract: Many-body interatomic potentials play an important role in a… read moreAbstract: Many-body interatomic potentials play an important role in atomistic modelling of materials. For pure elements it is known that there exist gauge transformations that can change the form of the potential functions without modifying its properties. These same transformations, however, fail when applied to alloys. Even though different research groups may use the same potentials to describe pure elements, the gauges employed for fitting alloys will generally be different. In this scenario, it is a priori impossible to merge them into one potential describing the combined system, and thus no advantage is taken from state-of-the-art developments in the literature. Here, we generalise the gauge transformations applied to pure species in order to leave the properties of alloys invariant. Based on these transformations, a strategy to merge potentials developed within different gauges is presented, aiming at the description of the combined system. Advantage of existing state-of-the-art potentials is so taken, thus focusing the efforts on fitting only the missing interactions. Such a procedure constitutes a helpful tool for the development of potentials targeted to alloys of increased complexity, while maintaining the description quality of their constituents. read less NOT USED (high confidence) N. Castin and L. Malerba, “Calculation of proper energy barriers for atomistic kinetic Monte Carlo simulations on rigid lattice with chemical and strain field long-range effects using artificial neural networks.,” The Journal of chemical physics. 2010. link Times cited: 49 Abstract: In this paper we take a few steps further in the development… read moreAbstract: In this paper we take a few steps further in the development of an approach based on the use of an artificial neural network (ANN) to introduce long-range chemical effects and zero temperature relaxation (elastic strain) effects in a rigid lattice atomistic kinetic Monte Carlo (AKMC) model. The ANN is trained to predict the vacancy migration energies as calculated given an interatomic potential with the nudged elastic band method, as functions of the local atomic environment. The kinetics of a single-vacancy migration is thus predicted as accurately as possible, within the limits of the given interatomic potential. The detailed procedure to apply this method is described and analyzed in detail. A novel ANN training algorithm is proposed to deal with the necessarily large number of input variables to be taken into account in the mathematical regression of the migration energies. The application of the ANN-based AKMC method to the simulation of a thermal annealing experiment in Fe-20%Cr alloy is reported. The results obtained are found to be in better agreement with experiments, as compared to already published simulations, where no atomic relaxation was taken into account and chemical effects were only heuristically allowed for. read less NOT USED (high confidence) C. Galvin, R. Grimes, and P. Burr, “A molecular dynamics method to identify the liquidus and solidus in a binary phase diagram,” Computational Materials Science. 2021. link Times cited: 6 NOT USED (high confidence) C. Becquart, N. Mousseau, and C. Domain, “Kinetic Monte Carlo Simulations of Irradiation Effects,” Comprehensive Nuclear Materials. 2020. link Times cited: 16 NOT USED (high confidence) B. Cheng, “Predicting homogeneous nucleation rate from atomistic simulations.” 2019. link Times cited: 0 Abstract: Nucleation is ubiquitous, from the formation of clouds to th… read moreAbstract: Nucleation is ubiquitous, from the formation of clouds to the preparation of pharmaceutical compounds, from metal casting to the tempering of chocolates, and from the growth of beautiful nautilus shells to the assembly of microtubules in cells. The first experiment for observing a nucleation event was performed by Fahrenheit in 1724, and it can be easily replicated in a kitchen: simply place a bottle of purified water in the freezer. The liquid water can be cooled to far below zero degrees Celsius without freezing due to the lack of microscopic nuclei, which are the embryos from which the freezing phase transition can occur. After that, shaking the bottle will induce nucleation which in turn prompts a rapid ice crystallization. Despite its pivotal importance and long history, we only have a rough idea about the underlying mechanism of nucleation. The classical nucleation theory says that, during the growth of a nucleus inside a bulk phase, an interface that surrounds the nucleus has to be created. This interface is associated with an energy penalty, which the system has to overcome for the nucleus to grow into a critical size which precedes an avalanche of structural transitions. It is analogous to being stuck in a valley on the Alps, so that a great deal of time and energy have to be spent to climb over a peak in order to reach another valley. And yet, we have not reached a quantitative understanding of how high the energy barrier is and how long is the waiting time of nucleation for specific systems. Taking again the example of ice nucleation from bulk liquid water, there has been a long-standing discrepancy by more than 10 orders of magnitude between the measured and the predicted expectation time of nucleation. While the classical nucleation theory is able to paint a physical picture of nucleation, for many systems it is insufficient and thus needs extension. Despite substantial improvements in recent years, experimental characterization of the dynamical nucleation processes is extremely difficult, which motivates atomistic modelling efforts that use numerical simulation techniques. However, atomistic simulations also faces a number of challenges: firstly the typical time scales accessible to atomistic simulations are confined to below microseconds, while nucleation can take hours or days to occur. We have mitigated the challenge by employing state-of-the-art enhanced sampling methods in the simulation studies of nucleation [1–5]. In a nutshell, instead of naively waiting for a rare event to happen, we place a bias to help the system overcome the energy penalty of nucleation. To return to the earlier analogy with Alpine hiking, we can flatten out the Alps by depositing (a lot of) sand into all the valleys, making the landscape level and easy to explore. Secondly, only microscopic quantities such as the coordinates and the velocities of each atom can be directly obtained from simulations. On the contrary, macroscopic observables read less NOT USED (high confidence) J. S. Gibson, S. G. Srinivasan, M. Baskes, R. E. Miller, and A. K. Wilson, “A multi-state modified embedded atom method potential for titanium,” Modelling and Simulation in Materials Science and Engineering. 2016. link Times cited: 3 Abstract: The continuing search for broadly applicable, predictive, an… read moreAbstract: The continuing search for broadly applicable, predictive, and unique potential functions led to the invention of the multi-state modified embedded atom method (MS-MEAM) (Baskes et al 2007 Phys. Rev. B 75 094113). MS-MEAM replaced almost all of the prior arbitrary choices of the MEAM electron densities, embedding energy, pair potential, and angular screening functions by using first-principles computations of energy/volume relationships for multiple reference crystal structures and transformation paths connecting those reference structures. This strategy reasonably captured diverse interactions between atoms with variable coordinations in a face-centered-cubic (fcc)-stable copper system. However, a straightforward application of the original MS-MEAM framework to model technologically useful hexagonal-close-packed (hcp) metals proved elusive. This work describes the development of an hcp-stable/fcc-metastable MS-MEAM to model titanium by introducing a new angular function within the background electron density description. This critical insight enables the titanium MS-MEAM potential to reproduce first principles computations of reference structures and transformation paths extremely well. Importantly, it predicts lattice and elastic constants, defect energetics, and dynamics of non-ideal hcp and liquid titanium in good agreement with first principles computations and corresponding experiments, and often better than the three well-known literature models used as a benchmark. The titanium MS-MEAM has been made available in the Knowledgebase of Interatomic Models (https://openkim.org/) (Tadmor et al 2011 JOM 63 17). read less NOT USED (definite) Ž. Božić, S. Schmauder, M. Mlikota, and M. Hummel, “Multiscale fatigue crack growth modelling for welded stiffened panels,” Fatigue & Fracture of Engineering Materials & Structures. 2014. link Times cited: 72 Abstract: The influence of welding residual stresses in stiffened pane… read moreAbstract: The influence of welding residual stresses in stiffened panels on effective stress intensity factor (SIF) values and fatigue crack growth rate is studied in this paper. Interpretation of relevant effects on different length scales such as dislocation appearance and microstruc- tural crack nucleation and propagation is taken into account using molecular dynamics simulations as well as a Tanaka-Mura approach for the analysis of the problem. Mode I SIFs, KI, were calculated by the finite element method using shell elements and the crack tip displacement extrapolation technique. The total SIF value, Ktot, is derived by a part due to the applied load, Kappl, and by a part due to welding residual stresses, Kres. Fatigue crack propagation simulations based on power law models showed that high tensile residual stresses in the vicinity of a stiffener significantly increase the crack growth rate, which is in good agreement with experimental results. read less |
 EAM_Dynamo_BonnyPasianotCastin_2009_FeCuNi__MO_469343973171_005
EAM_Dynamo_BonnyPasianotCastin_2009_FeCuNi__MO_469343973171_005