EAM_Dynamo_BonnyPasianotCastin_2009_FeCuNi__MO_469343973171_005
EAM_Dynamo_BonnyPasianotCastin_2009_FeCuNi__MO_469343973171_005
| Title
A single sentence description.
|
EAM potential (LAMMPS cubic hermite tabulation) for Fe-Cu-Ni reactor pressure vessel steels developed by Bonny et al. (2009) v005 |
|---|---|
| Description
A short description of the Model describing its key features including for example: type of model (pair potential, 3-body potential, EAM, etc.), modeled species (Ac, Ag, ..., Zr), intended purpose, origin, and so on.
|
Ternary FeCuNi EAM-type potential. The fitting was focused on solute-point defect interaction in the bcc Fe matrix. With respect to thermodynamics the following was accounted for: experimentally observed intermetallic compounds in the FeNi alloys, the Cu solubility in the FeCu binary and the CuNi miscibility gap. The potential is designed to model radiation damage in the FeCuNi model alloy which represents reactor pressure vessel steels. FeNi cross potential is taken from [Bonny et. al., Modelling Simul. Mater. Sci. Eng. 17 (2009) 025010]. FeCu cross potential is taken from [Pasianot and Malerba, J. Nucl. Mater. 360 (2007) 118]. Fe potential is taken from [Mendelev et al., Philos. Mag. 83 (2003) 3977]. Ni potential is taken from [Voter and Chen, Mater. Res. Soc. Symp. Proc. 82 (1987) 175]. Cu potential is taken from [Mishin et al., Phys. Rev. B 63 (2001) 224106]. |
| Species
The supported atomic species.
| Cu, Fe, Ni |
| Disclaimer
A statement of applicability provided by the contributor, informing users of the intended use of this KIM Item.
|
The potential is stiffened. |
| Content Origin | http://www.ctcms.nist.gov/potentials/Fe.html |
| Contributor |
Giovanni Bonny |
| Maintainer |
Giovanni Bonny |
| Developer |
Giovanni Bonny Roberto C Pasianot N. Castin L. Malerba |
| Published on KIM | 2018 |
| How to Cite |
This Model originally published in [1] is archived in OpenKIM [2-5]. [1] Bonny G, Pasianot RC, Castin N, Malerba L. Ternary Fe–Cu–Ni many-body potential to model reactor pressure vessel steels: First validation by simulated thermal annealing. Philosophical Magazine. 2009;89(34-36):3531–46. doi:10.1080/14786430903299824 — (Primary Source) A primary source is a reference directly related to the item documenting its development, as opposed to other sources that are provided as background information. [2] Bonny G, Pasianot RC, Castin N, Malerba L. EAM potential (LAMMPS cubic hermite tabulation) for Fe-Cu-Ni reactor pressure vessel steels developed by Bonny et al. (2009) v005. OpenKIM; 2018. doi:10.25950/23db26d9 [3] Foiles SM, Baskes MI, Daw MS, Plimpton SJ. EAM Model Driver for tabulated potentials with cubic Hermite spline interpolation as used in LAMMPS v005. OpenKIM; 2018. doi:10.25950/68defa36 [4] Tadmor EB, Elliott RS, Sethna JP, Miller RE, Becker CA. The potential of atomistic simulations and the Knowledgebase of Interatomic Models. JOM. 2011;63(7):17. doi:10.1007/s11837-011-0102-6 [5] Elliott RS, Tadmor EB. Knowledgebase of Interatomic Models (KIM) Application Programming Interface (API). OpenKIM; 2011. doi:10.25950/ff8f563a Click here to download the above citation in BibTeX format. |
| Citations
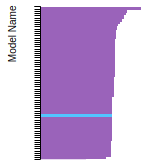
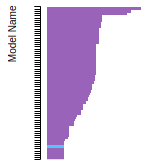
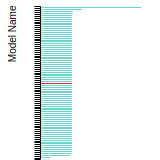
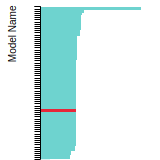
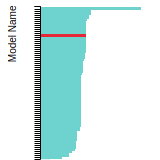
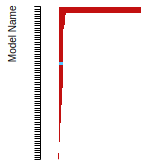
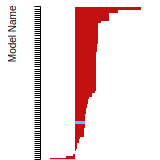
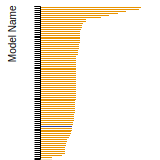
This panel presents information regarding the papers that have cited the interatomic potential (IP) whose page you are on. The OpenKIM machine learning based Deep Citation framework is used to determine whether the citing article actually used the IP in computations (denoted by "USED") or only provides it as a background citation (denoted by "NOT USED"). For more details on Deep Citation and how to work with this panel, click the documentation link at the top of the panel. The word cloud to the right is generated from the abstracts of IP principle source(s) (given below in "How to Cite") and the citing articles that were determined to have used the IP in order to provide users with a quick sense of the types of physical phenomena to which this IP is applied. The bar chart shows the number of articles that cited the IP per year. Each bar is divided into green (articles that USED the IP) and blue (articles that did NOT USE the IP). Users are encouraged to correct Deep Citation errors in determination by clicking the speech icon next to a citing article and providing updated information. This will be integrated into the next Deep Citation learning cycle, which occurs on a regular basis. OpenKIM acknowledges the support of the Allen Institute for AI through the Semantic Scholar project for providing citation information and full text of articles when available, which are used to train the Deep Citation ML algorithm. |
This panel provides information on past usage of this interatomic potential (IP) powered by the OpenKIM Deep Citation framework. The word cloud indicates typical applications of the potential. The bar chart shows citations per year of this IP (bars are divided into articles that used the IP (green) and those that did not (blue)). The complete list of articles that cited this IP is provided below along with the Deep Citation determination on usage. See the Deep Citation documentation for more information. 
199 Citations (168 used)
Help us to determine which of the papers that cite this potential actually used it to perform calculations. If you know, click the .
USED (definite) M. Munaji, G. A. Buntoro, A. Purniawan, and R. Arifin, “Molecular Dynamics Simulations of Iron-Joining Using Copper as a Filler Metal,” Makara Journal of Science. 2018. link Times cited: 2 Abstract: The study of the liquid filler metal infiltration on the nar… read more USED (definite) Y. Cheng, W. Cui, L. Wang, C. Peng, S. Wang, and Y.-yang Wang, “Vitrification and Crystallization of Phase-Separated Metallic Liquid.” 2017. link Times cited: 5 Abstract: The liquid–liquid phase separation (LLPS) behavior of Fe50Cu… read more USED (definite) S. Shao and J. Wang, “Relaxation Mechanisms, Structure and Properties of Semi-Coherent Interfaces.” 2015. link Times cited: 10 Abstract: In this work, using the Cu–Ni (111) semi-coherent interface … read more USED (high confidence) B. Waters, D. S. Karls, I. Nikiforov, R. Elliott, E. Tadmor, and B. Runnels, “Automated determination of grain boundary energy and potential-dependence using the OpenKIM framework,” Computational Materials Science. 2022. link Times cited: 5 USED (high confidence) W. Guo, C. Wu, X. Meng, C. Luo, and Z. Lin, “Molecular dynamics simulation-based microstructure evolution and subsurface damage of Fe-Ni alloy grinding,” Journal of Intelligent Manufacturing and Special Equipment. 2022. link Times cited: 0 Abstract: PurposeMolecular dynamics is an emerging simulation techniqu… read more USED (high confidence) M. Fokt, G. Adjanor, and T. Jourdan, “A variable-gap model for helium bubbles in nickel,” Computational Materials Science. 2022. link Times cited: 1 USED (high confidence) S. Mori, N. Matsuda, T. Okita, M. Aichi, M. Itakura, and K. Suzuki, “Modeling Changes in the Second Harmonic Generation of Ultrasonic Waves Having Wavelengths Beyond the Length Scale of Conventional Molecular Dynamics,” MatSciRN: Other Electronic. 2022. link Times cited: 3 Abstract: The nonlinear ultrasonic (NLU) technique is attracting atten… read more USED (high confidence) L. Xu, L. Casillas-Trujillo, Y. Gao, and H. Xu, “Compositional effects on stacking fault energies in Ni-based alloys using first-principles and atomistic simulations,” Computational Materials Science. 2021. link Times cited: 5 USED (high confidence) H. Zhang, Y.-li Chen, X. Wang, H. Li, and Y. Li, “Molecular Dynamics Research on the Impact of Vacancies on Cu Precipitation in BCC-Fe,” Materials. 2021. link Times cited: 0 Abstract: The molecular dynamics (MD) simulation method was used to ex… read more USED (high confidence) S. Dong, X.-Y. Liu, and C. Zhou, “Atomistic modeling of plastic deformation in B2-FeAl/Al nanolayered composites,” Journal of Materials Science. 2021. link Times cited: 0 USED (high confidence) S. Eder, P. Grützmacher, M. R. Ripoll, and J. Belak, “Elucidating the Onset of Plasticity in Sliding Contacts Using Differential Computational Orientation Tomography,” Tribology Letters. 2021. link Times cited: 9 USED (high confidence) X. Xu, P. Binkele, W. Verestek, and S. Schmauder, “Molecular Dynamics Simulation of High-Temperature Creep Behavior of Nickel Polycrystalline Nanopillars,” Molecules. 2021. link Times cited: 0 Abstract: As Nickel (Ni) is the base of important Ni-based superalloys… read more USED (high confidence) K. Kanamori, S. Toriumi, Y. Kimoto, and A. Yonezu, “Repeated Laser Shock-Wave Adhesion Test for Metallic Coatings: Adhesion Durability and Its Mechanism Studied by Molecular Dynamics Simulation,” Coatings. 2021. link Times cited: 2 Abstract: We evaluated the adhesion of polycrystalline metallic coatin… read more USED (high confidence) K. Chen et al., “Molecular Dynamics Simulations of High-speed Nanoscale Sliding with Third Medium,” IOP Conference Series: Earth and Environmental Science. 2021. link Times cited: 0 Abstract: 3D non-equilibrium molecular dynamics simulations are perfor… read more USED (high confidence) W. Nöhring, J.-C. Griesser, P. Dondl, and L. Pastewka, “Surface lattice Green’s functions for high-entropy alloys,” Modelling and Simulation in Materials Science and Engineering. 2021. link Times cited: 0 Abstract: We study the surface elastic response of pure Ni, the random… read more USED (high confidence) H. Zhang, X. Wang, L. Huirong, C. Li, and L. Yungang, “Molecular Dynamics Study on the Impact of Cu Clusters at the BCC-Fe Grain Boundary on the Tensile Properties of Crystal,” Metals. 2020. link Times cited: 3 Abstract: The molecular dynamics (MD) method was used to simulate and … read more USED (high confidence) J. Chen, P. Li, and E. E. Lin, “A molecular dynamics study on the mechanical properties of Fe–Ni alloy nanowires and their temperature dependence,” RSC Advances. 2020. link Times cited: 7 Abstract: Fe–Ni alloy nanowires are widely used in high-density magnet… read more USED (high confidence) M. Wang, G. Zhang, H. Xu, and Y. Zhang, “Atomistic Simulations and Experimental Investigations of the Diffusion Behavior of Steel/ZCuPb20Sn5 Bimetals,” THE Coatings. 2020. link Times cited: 3 Abstract: A hybrid verification method consisting of experiments and m… read more USED (high confidence) L.-F. Zhu, F. Körmann, A. Ruban, J. Neugebauer, and B. Grabowski, “Performance of the standard exchange-correlation functionals in predicting melting properties fully from first principles: Application to Al and magnetic Ni,” Physical Review B. 2020. link Times cited: 10 Abstract: We apply the efficient two-optimized references thermodynami… read more USED (high confidence) R. Khusnutdinoff, R. Khairullina, A. Beltyukov, V. Lad’yanov, and A. Mokshin, “Viscous properties of nickel-containing binary metal melts,” Journal of Physics: Condensed Matter. 2020. link Times cited: 0 Abstract: The paper presents the results of molecular dynamics study o… read more USED (high confidence) O. Filatov and O. Soldatenko, “Influence of Glide Dislocation Motion on Self-Diffusion in b.c.c. Fe. A Molecular Dynamics Study,” Metallofizika I Noveishie Tekhnologii. 2020. link Times cited: 1 Abstract: The interaction of glide dislocations with own interstitial … read more USED (high confidence) A. Tsukanov et al., “Effect of Cold-Sintering Parameters on Structure, Density, and Topology of Fe–Cu Nanocomposites,” Materials. 2020. link Times cited: 8 Abstract: The design of advanced nanostructured materials with predete… read more USED (high confidence) J. Sublet et al., “Neutron-induced damage simulations: Beyond defect production cross-section, displacement per atom and iron-based metrics,” The European Physical Journal Plus. 2019. link Times cited: 22 USED (high confidence) A. Tsukanov, A. Lozhkomoev, M. Lerner, I. Gotman, E. Gutmanas, and S. Psakhie, “Molecular dynamics study of bimetallic Fe–Cu Janus nanoparticles formation by electrical explosion of wires,” Philosophical Magazine. 2019. link Times cited: 3 Abstract: ABSTRACT Bimetallic nanoparticles comprised of two elements … read more USED (high confidence) M. R. Karim, M. Kattoura, S. Mannava, V. Vasudevan, A. Malik, and D. Qian, “A computational study on the microstructural evolution in near-surface copper grain boundary structures due to femtosecond laser processing,” Computational Mechanics. 2018. link Times cited: 6 USED (high confidence) M. R. Karim, M. Kattoura, S. Mannava, V. Vasudevan, A. Malik, and D. Qian, “A computational study on the microstructural evolution in near-surface copper grain boundary structures due to femtosecond laser processing,” Computational Mechanics. 2017. link Times cited: 0 USED (high confidence) J. Zhou et al., “Zener pinning by coherent particles: pinning efficiency and particle reorientation mechanisms,” Modelling and Simulation in Materials Science and Engineering. 2017. link Times cited: 13 Abstract: Zener pinning by coherent particles in copper–nickel model a… read more USED (high confidence) I. N. Kar’kin, L. E. Kar’kina, P. Korzhavyi, and Y. Gornostyrev, “Monte Carlo simulation of the kinetics of decomposition and the formation of precipitates at grain boundaries of the general type in dilute BCC Fe–Cu alloys,” Physics of the Solid State. 2017. link Times cited: 8 USED (high confidence) W. Cui et al., “Up-Hill Diffusion of Phase-Separated FeCu Melt by Molecular Dynamics Simulation,” Chinese Physics Letters. 2017. link Times cited: 2 USED (high confidence) W. Tucker and P. Schelling, “Thermodiffusion in liquid binary alloys computed from molecular-dynamics simulation and the Green-Kubo formalism,” Computational Materials Science. 2016. link Times cited: 8 USED (high confidence) C. Race, “Quantifying uncertainty in molecular dynamics simulations of grain boundary migration,” Molecular Simulation. 2015. link Times cited: 17 Abstract: Molecular dynamics simulations of simple bicrystal systems h… read more USED (high confidence) D. Molnár, U. Weber, P. Binkele, D. Rapp, and S. Schmauder, “Prediction of macroscopic damage behaviour of precipitation strengthened steels via multiscale simulations,” GAMM‐Mitteilungen. 2015. link Times cited: 6 Abstract: A multiscale modelling approach is presented that sequential… read more USED (high confidence) G. Lv, H. Zhang, X. He, W. Yang, and Y. Su, “Atomistic simulation of Cu–Ni precipitates hardening in α-iron,” Journal of Physics D: Applied Physics. 2015. link Times cited: 7 Abstract: In this paper, we investigated the interaction of an edge di… read more USED (high confidence) L. Shao et al., “Sink property of metallic glass free surfaces,” Scientific Reports. 2015. link Times cited: 18 USED (high confidence) S. Vigonski, F. Djurabekova, M. Veske, A. Aabloo, and V. Zadin, “Molecular dynamics simulations of near-surface Fe precipitates in Cu under high electric fields,” Modelling and Simulation in Materials Science and Engineering. 2015. link Times cited: 14 Abstract: High electric fields in particle accelerators cause vacuum b… read more USED (high confidence) S. Shao, J. Wang, and A. Misra, “Energy minimization mechanisms of semi-coherent interfaces,” Journal of Applied Physics. 2014. link Times cited: 51 Abstract: In this article, we discussed energy minimization mechanisms… read more USED (high confidence) Y. Satoh, H. Abe, and T. Matsunaga, “Radiation-induced glide motion of interstitial clusters in concentrated alloys,” Philosophical Magazine. 2014. link Times cited: 4 Abstract: We propose a mechanism for glide motion, i.e. one-dimensiona… read more USED (high confidence) T. Rupert, “Solid Solution Strengthening and Softening Due to Collective Nanocrystalline Deformation Physics,” arXiv: Materials Science. 2014. link Times cited: 34 USED (high confidence) S. Shao, J. Wang, A. Misra, and R. Hoagland, “Spiral Patterns of Dislocations at Nodes in (111) Semi-coherent FCC Interfaces,” Scientific Reports. 2013. link Times cited: 91 USED (high confidence) D. Molnár, P. Binkele, S. Hocker, and S. Schmauder, “Atomistic multiscale simulations on the anisotropic tensile behaviour of copper-alloyed alpha-iron at different states of thermal ageing,” Philosophical Magazine. 2012. link Times cited: 18 Abstract: The mechanical behaviour of steels is strongly related to th… read more USED (low confidence) S. Kumar, A. Rajput, S. K. Paul, M. Tiwari, and D. K. Prajapati, “Friction and wear study of metallic contacts under dry sliding conditions: A molecular dynamics simulation-based approach,” Proceedings of the Institution of Mechanical Engineers, Part J: Journal of Engineering Tribology. 2023. link Times cited: 0 Abstract: Sliding friction originating due to ploughing and adhesive w… read more USED (low confidence) Y. He, Z. Gao, M. Tang, X. Sun, P. Gao, and J. Sun, “Characteristics of atomic removal and mechanism of damage formation in vibration-assisted nano cutting of copper-nickel alloy,” Materials Today Communications. 2023. link Times cited: 0 USED (low confidence) X. Zhu, X. Wang, Y. Liu, Y. Luo, and H. Zhang, “Probing the Effect of Cuttings Particle Size on the Friction and Wear Mechanism at the Casing Friction Interface: A Molecular Dynamics Study.,” Langmuir : the ACS journal of surfaces and colloids. 2023. link Times cited: 0 Abstract: Cuttings particles of different sizes in the drilling fluid … read more USED (low confidence) A. Kumar, R. Kumar, S. Kumar, and A. K. V, “Atomistic structural transformation of Fe-Cr-Ni single crystal alloy under uniaxial deformation using molecular dynamics simulation,” Materials Today: Proceedings. 2023. link Times cited: 0 USED (low confidence) D. Tramontina et al., “Probing radiation resistance in simulated metallic core–shell nanoparticles,” Computational Materials Science. 2023. link Times cited: 0 USED (low confidence) T. Zhou, Y. Wu, and J.-J. You, “Evolution of the shape and microstructure of body-centered cubic seeds during Cu melt solidification,” Chemical Physics Letters. 2023. link Times cited: 0 USED (low confidence) N. Wang et al., “An experimental and molecular dynamics study on the formation of low-energy grain boundaries induced by grain rotation during rapid solidification,” Materials Letters. 2023. link Times cited: 0 USED (low confidence) W. Pang, X.-jing Feng, R. Chen, A. Liu, and K. Xin, “Molecular dynamics studies of the effect of intermediate Fe layer thickness on the enhanced strength and ductility of Cu/Fe/Ni multilayer,” Physica Scripta. 2023. link Times cited: 0 Abstract: The synergistic strength-ductility is very important for com… read more USED (low confidence) R. Barik, S. Biswal, A. Dutta, D. Chakrabarti, and A. Ghosh, “Effect of solute distribution on the screw dislocation motion in bcc Fe-based systems,” Computational Materials Science. 2023. link Times cited: 0 USED (low confidence) A. Dmitriev and A. Nikonov, “Molecular-Dynamic Study of the Interfacial Zone of Dissimilar Metals Under Compression and Shear,” Russian Physics Journal. 2023. link Times cited: 0 USED (low confidence) S. Yang, H. Bao, H. Bai, Y. Li, H. Xu, and F. Ma, “Effects of Fe solid solute on grain boundaries of bi-crystal Cu: A molecular dynamics simulation,” Nano Materials Science. 2023. link Times cited: 0 USED (low confidence) F. Wang et al., “Enhanced nanocrystalline stability of BCC iron via copper segregation,” Progress in Natural Science: Materials International. 2023. link Times cited: 4 USED (low confidence) “A physically-based constitutive model for a novel heat resistant martensitic steel under different cyclic loading modes: Microstructural strengthening mechanisms,” International Journal of Plasticity. 2023. link Times cited: 12 USED (low confidence) B. Li, R. Ma, S. Qin, and X. Zhang, “Regulating the dislocation-nanocluster interactions by electrical pulses to alleviate material hardening,” Materials Science and Engineering: A. 2023. link Times cited: 0 USED (low confidence) K. Bandyopadhyay, S. Das, K. S. Ghosh, and M. Ghosh, “Molecular Dynamics-Based Scheme of Designing Nanostructured Cu-Ni Alloy Thin Film for Coating on Advanced Structural Components in Naval Vessels,” Journal of Materials Engineering and Performance. 2022. link Times cited: 2 USED (low confidence) Y. Lei et al., “An Embedded-Atom Method Potential for studying the properties of Fe-Pb solid-liquid interface,” Journal of Nuclear Materials. 2022. link Times cited: 1 USED (low confidence) G. Zhang, M. Wang, H. Yu, H. Xu, and A. Wan, “Molecular Dynamics and Experimental Investigation on the Interfacial Binding Mechanism in the Fe/Cu1−x-Nix Bimetallic Interface,” Nanomaterials. 2022. link Times cited: 0 Abstract: To systematically investigate the diffusion behavior of Fe/C… read more USED (low confidence) K. Ren, L. Liu, J. Li, H. Pan, and Z. Wang, “Lubrication Behavior of n-hexadecane on ZnO Layer at the Nanoscale: A Molecular Dynamic Exploration,” Tribology Letters. 2022. link Times cited: 1 USED (low confidence) G. Dai, S. Wu, X. Huang, M.-jie Wang, and X. Teng, “Thermal diffusion behavior of Fe/Cu/Ni multilayer coatings: a molecular dynamics study,” Modelling and Simulation in Materials Science and Engineering. 2022. link Times cited: 1 Abstract: In this paper, the thermal diffusion behavior of Fe/Cu/Ni mu… read more USED (low confidence) Y. Deng et al., “Molecular dynamics simulation of the growth and diffusion mechanisms of Fe–Cu bimetallic nanoparticles,” Philosophical Magazine. 2022. link Times cited: 1 Abstract: ABSTRACT In accordance with the molecular dynamic simulation… read more USED (low confidence) D. Yang, H. Liu, Q. Jiang, Y. Jiang, X. Wang, and W. Yang, “Atomic-level understanding of weakening crystallization in additive manufactured ternary Fe-based metallic glasses with Ni addition,” Journal of Non-Crystalline Solids. 2022. link Times cited: 5 USED (low confidence) H. Bao, H. Xu, Y. Li, H. Bai, and F. Ma, “The interaction mechanisms between dislocations and nano-precipitates in CuFe alloys: a molecular dynamic simulation,” International Journal of Plasticity. 2022. link Times cited: 11 USED (low confidence) J. Syarif, V. Gillette, H. Hussien, K. Badawy, and N. Jisrawi, “Molecular dynamics simulation of the amorphization and alloying of a mechanically milled Fe-Cu system,” Journal of Non-Crystalline Solids. 2022. link Times cited: 1 USED (low confidence) I. Camacho et al., “On the anticorrosion mechanism of molten salts based nanofluids,” Solar Energy Materials and Solar Cells. 2022. link Times cited: 5 USED (low confidence) Z. Shi, B. Li, and Z. Sun, “Study on microstructure evolution of grinding surface of bcc Fe-Ni maraging steel based on molecular dynamics,” Applied Surface Science. 2022. link Times cited: 7 USED (low confidence) A. Mishra, J. Lind, M. Kumar, and A. Dongare, “Understanding the phase transformation mechanisms that affect the dynamic response of Fe-based microstructures at the atomic scales,” Journal of Applied Physics. 2021. link Times cited: 8 USED (low confidence) J. Yin, H. Hou, J. Wang, X. Liu, and F. Xue, “Atomistic simulation of [100](001) crack propagation with Cu precipitates in α-iron,” International Journal of Pressure Vessels and Piping. 2021. link Times cited: 4 USED (low confidence) C. Yi, C. Hu, L. Shi, M.-li Bai, and J. Lv, “Wettability of complex Long-Chain alkanes droplets on Pillar-type surfaces,” Applied Surface Science. 2021. link Times cited: 4 USED (low confidence) D. S. Sineglazov, S. Divinski, and A. V. Pokoev, “Simulation of the Magnetoplastic Effect in a Cu–Ni Alloy,” Journal of Surface Investigation: X-ray, Synchrotron and Neutron Techniques. 2021. link Times cited: 0 USED (low confidence) X.-jing Feng, Z. Lin, K. Xin, and W. Pang, “The deformation mechanisms and mechanical properties of Cu/Fe multilayer during compression process,” Journal of Materials Research. 2021. link Times cited: 4 Abstract: The deformation mechanisms and mechanical properties of Cu/F… read more USED (low confidence) X. Li, Z.-an Tian, Q. Xie, and K. Dong, “The topologically close-packed Fe70Cu15Ni15 nanoparticles- A simulation study,” Vacuum. 2021. link Times cited: 3 USED (low confidence) X.-Y. Liu, L. Capolungo, and A. Hunter, “Screw dislocation impingement and slip transfer at fcc-bcc semicoherent interfaces,” Scripta Materialia. 2021. link Times cited: 9 USED (low confidence) H. Xu, H. Bao, Y. Li, H. Bai, and F. Ma, “Atomic scale insights into the rapid crystallization and precipitation behaviors in FeCu binary alloys,” Journal of Alloys and Compounds. 2021. link Times cited: 5 USED (low confidence) Y. Li et al., “Shear-strain induced structural relaxation of Cu Σ3 [110](112) symmetric tilt grain boundary: The role of foreign atoms and temperature,” Current Applied Physics. 2021. link Times cited: 1 USED (low confidence) N. Eom, M. Messing, J. Johansson, and K. Deppert, “General Trends in Core–Shell Preferences for Bimetallic Nanoparticles,” ACS Nano. 2021. link Times cited: 36 Abstract: Surface segregation phenomena dictate core–shell preference … read more USED (low confidence) J. Syarif and K. Badawy, “Computational modelling of cold rolling of ferritic iron containing ε-Cu precipitates,” Materials today communications. 2021. link Times cited: 0 USED (low confidence) F. Tan, F. Li, Q. Fang, J. Li, and H. Feng, “Grain boundary migration and deformation mechanism influenced by heterogeneous precipitate,” Journal of Materials Science. 2021. link Times cited: 2 USED (low confidence) S. Eder, P. Grützmacher, M. R. Ripoll, and J. Belak, “Elucidating the Onset of Plasticity in Sliding Contacts Using Differential EBSD Tomography.” 2021. link Times cited: 0 Abstract:
Depending on the mechanical and thermal energy introduced … read more USED (low confidence) Z. Lin, W. Pang, K. Xin, X.-jing Feng, and F. Yin, “The effect of loading strain rates on deformation behavior of Cu/Fe composite,” Physics Letters A. 2021. link Times cited: 5 USED (low confidence) S. Eder, P. Grützmacher, M. R. Ripoll, D. Dini, and C. Gachot, “Effect of Temperature on the Deformation Behavior of Copper Nickel Alloys under Sliding,” Materials. 2020. link Times cited: 18 Abstract: The microstructural evolution in the near-surface regions of… read more USED (low confidence) H. Wang, X. Gao, S. Chen, L. Yiming, Z.-wang Wu, and H. Ren, “Effects of Al on the precipitation of B2 Cu-rich particles in Fe–Cu ferritic alloy: Experimental and theoretical study,” Journal of Alloys and Compounds. 2020. link Times cited: 5 USED (low confidence) A. Garrett and C. Race, “Cu nanoprecipitate morphologies and interfacial energy densities in bcc Fe from density functional theory (DFT),” Computational Materials Science. 2020. link Times cited: 7 USED (low confidence) J. Li, Z.-an Tian, Q. Xie, and S. Xiong, “Component effect on microstructure of rapidly cooled FeCuNi alloys,” Chemical Physics Letters. 2020. link Times cited: 4 USED (low confidence) M. Ghaemi and R. Tavakoli, “Universal correlation between the thermodynamic potentials and some physical quantities of metallic glasses as a function of cooling rate during molecular dynamics simulation,” Journal of Non-crystalline Solids. 2020. link Times cited: 2 USED (low confidence) B. Yao and R. F. Zhang, “AADIS: An atomistic analyzer for dislocation character and distribution,” Comput. Phys. Commun. 2020. link Times cited: 19 USED (low confidence) S. Kumar, “Structural Evolution of Iron–Copper (Fe–Cu) Bimetallic Janus Nanoparticles during Solidification: An Atomistic Investigation,” Journal of Physical Chemistry C. 2020. link Times cited: 15 Abstract: Bimetallic nanoparticles consist of two different metallic e… read more USED (low confidence) Z. Sun, F. Z. Dai, B. Xu, and W.-Z. Zhang, “Dislocation-mediated migration of interphase boundaries,” Journal of Materials Science & Technology. 2019. link Times cited: 7 USED (low confidence) J. Yin, Y. Wang, H. Hou, J. Wang, X. Liu, and F. Xue, “Atomistic simulation of interactions between an edge dislocation and Cu precipitates with different chemical compositions in α-Fe,” Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms. 2019. link Times cited: 4 USED (low confidence) J. Chen et al., “Dynamics simulation study on crystallization of amorphous Ni-Fe alloy,” Ferroelectrics. 2019. link Times cited: 1 Abstract: Molecular dynamics simulation was performed to study the cry… read more USED (low confidence) M. Hummel, C. Böhm, W. Verestek, and S. Schmauder, “Introducing a method of constructing realistic closed cell nano-porous iron crystals and MD simulations to investigate the influence of the system size on the stability and the mechanical properties,” Computational Materials Science. 2019. link Times cited: 4 USED (low confidence) H. Luu and N. Gunkelmann, “Pressure-induced phase transformations in Fe-C: Molecular dynamics approach,” Computational Materials Science. 2019. link Times cited: 24 USED (low confidence) G. Bonny, C. Domain, N. Castin, P. Olsson, and L. Malerba, “The impact of alloying elements on the precipitation stability and kinetics in iron based alloys: An atomistic study,” Computational Materials Science. 2019. link Times cited: 27 USED (low confidence) L. Li, Q. Fang, J. Li, and H. Wu, “Origin of strengthening-softening trade-off in gradient nanostructured body-centred cubic alloys,” Journal of Alloys and Compounds. 2019. link Times cited: 12 USED (low confidence) C. Zhang, K. Ma, N. Zhao, and Z. Yuan, “A Core–Shell Strategy for Improving Alloy Catalyst Activity for Continual Growth of Hollow Carbon Onions,” Crystal Growth & Design. 2018. link Times cited: 9 Abstract: Herein, we report the controlled synthesis of hollow carbon … read more USED (low confidence) H. N. Pishkenari, F. S. Yousefi, and A. Taghibakhshi, “Determination of surface properties and elastic constants of FCC metals: a comparison among different EAM potentials in thin film and bulk scale,” Materials Research Express. 2018. link Times cited: 22 Abstract: Three independent elastic constants C11, C12, and C44 were c… read more USED (low confidence) Y. Zhang, D. Schwen, and X. Bai, “Effects of solute-SIA binding energy on defect production behaviors in Fe-based alloys,” Journal of Nuclear Materials. 2018. link Times cited: 6 USED (low confidence) Q. Fang, L. Li, J. Li, and H. Wu, “Strengthening mechanism of gradient nanostructured body-centred cubic iron film: From inverse Hall-Petch to classic Hall-Petch,” Computational Materials Science. 2018. link Times cited: 19 USED (low confidence) P. M. Sepúlveda et al., “As(V) removal capacity of FeCu bimetallic nanoparticles in aqueous solutions: The influence of Cu content and morphologic changes in bimetallic nanoparticles.,” Journal of colloid and interface science. 2018. link Times cited: 53 USED (low confidence) S. Eder, U. Cihak-Bayr, C. Gachot, and M. R. Ripoll, “Interfacial Microstructure Evolution Due to Strain Path Changes in Sliding Contacts.,” ACS applied materials & interfaces. 2018. link Times cited: 16 Abstract: We performed large-scale molecular dynamics (MD) simulations… read more USED (low confidence) N. Castin et al., “Advanced atomistic models for radiation damage in Fe-based alloys: Contributions and future perspectives from artificial neural networks,” Computational Materials Science. 2018. link Times cited: 21 USED (low confidence) A. Gola, P. Gumbsch, and L. Pastewka, “Atomic-scale simulation of structure and mechanical properties of Cu1−xAgx|Ni multilayer systems,” Acta Materialia. 2018. link Times cited: 17 USED (low confidence) W. Cui, L. Wang, C. Peng, and K. Song, “Phase separation and structure transition of undercooled Fe75Cu25 melts,” Physics and Chemistry of Liquids. 2018. link Times cited: 2 Abstract: ABSTRACT The rapid quenching processes of Fe75Cu25 melt at d… read more USED (low confidence) J. Lu, S. Ma, X.-X. Wang, and S. Wang, “The cluster-plus-glue-atom models of solid solution CuNi alloys: A first-principles study,” Computational Materials Science. 2018. link Times cited: 3 USED (low confidence) S. Shao, F. Akasheh, J. Wang, and Y. Liu, “Alternative misfit dislocations pattern in semi-coherent FCC 100 interfaces,” Acta Materialia. 2018. link Times cited: 26 USED (low confidence) X. Y. Chen et al., “Effect of dynamic evolution of misfit dislocation pattern on dislocation nucleation and shear sliding at semi-coherent bimetal interfaces,” Acta Materialia. 2018. link Times cited: 43 USED (low confidence) J. Li, Q. Fang, B. Liu, Y. Liu, and C. Jiang, “Twinning-governed plastic deformation in a thin film of body-centred cubic nanocrystalline ternary alloys at low temperature,” Journal of Alloys and Compounds. 2017. link Times cited: 22 USED (low confidence) A.Younes, N.Dilmi, M.Khorchef, A.Bouamer, N. Bacha, and M.Zergoug, “Structural and magnetic properties of FeCuNi nanostructured produced by mechanical alloying,” Applied Surface Science. 2017. link Times cited: 0 USED (low confidence) R. Jiang, A. Li, G. Cui, C. Zhang, H. Chen, and Y. Wang, “Influence of Ni-P content on microstructure and mechanical properties of Fe-x(Ni+P)-1Cu alloys,” Materials Science and Engineering A-structural Materials Properties Microstructure and Processing. 2017. link Times cited: 4 USED (low confidence) M. Kozłowski, D. Scopece, J. Janczak-Rusch, L. Jeurgens, R. Abdank-Kozubski, and D. Passerone, “Validation of an Embedded-Atom Copper Classical Potential via Bulk and Nanostructure Simulations,” Diffusion Foundations. 2017. link Times cited: 0 Abstract: The validation of classical potentials for describing multic… read more USED (low confidence) Y. Wang, J. Yin, X. Liu, R. Wang, H. Hou, and J. Wang, “Precipitation kinetics in binary Fe–Cu and ternary Fe–Cu–Ni alloys via kMC method,” Progress in Natural Science: Materials International. 2017. link Times cited: 15 USED (low confidence) K. Zolnikov, D. S. Kryzhevich, and A. Korchuganov, “Computer simulation of metal wire explosion under high rate heating,” Journal of Physics: Conference Series. 2017. link Times cited: 0 Abstract: Synchronous electric explosion of metal wires and synthesis … read more USED (low confidence) G. Lv and Y. Su, “Molecular dynamics simulation and first principles calculations of radiation-induced Cu clusters in Fe-3 at.% Cu alloy,” Comput. Phys. Commun. 2017. link Times cited: 5 USED (low confidence) S. Fazeli, M. Vahedpour, and S. Sadrnezhaad, “What is the copper thin film thickness effect on thermal properties of NiTi/Cu bi-layer?,” Materials Research Express. 2017. link Times cited: 0 Abstract: Molecular dynamics (MD) simulation was used to study of ther… read more USED (low confidence) S. Fazeli, M. Vahedpour, and S. Sadrnezhaad, “Comparison of the mechanical properties of NiTi/Cu bilayer by nanoindentation and tensile test: molecular dynamics simulation,” Materials Research Express. 2016. link Times cited: 5 Abstract: Molecular dynamics simulation was used to study of mechanica… read more USED (low confidence) K. Liu, R. Zhang, I. Beyerlein, X. Y. Chen, H. Yang, and T. Germann, “Cooperative dissociations of misfit dislocations at bimetal interfaces,” APL Materials. 2016. link Times cited: 18 Abstract: Using atomistic simulations, several semi-coherent cube-on-c… read more USED (low confidence) K. Zolnikov, D. S. Kryzhevich, and A. Korchuganov, “Features of particle synthesis at metal wire dispersion.” 2016. link Times cited: 0 Abstract: Features of particle synthesis under simultaneous dispersion… read more USED (low confidence) J. Li, Q. Fang, B. Liu, and Y.-wen Liu, “The effects of pore and second-phase particle on the mechanical properties of machining copper matrix from molecular dynamic simulation,” Applied Surface Science. 2016. link Times cited: 28 USED (low confidence) D. H. Chung, H. Guk, S.-H. Choi, and D. Kim, “Wettability of Ag nanocluster on Cu-Ni alloys: A computational approach,” Journal of Alloys and Compounds. 2016. link Times cited: 5 USED (low confidence) C. Peng, K. Song, L. Wang, D. Şopu, S. Pauly, and J. Eckert, “Correlation between structural heterogeneity and plastic deformation for phase separating FeCu metallic glasses,” Scientific Reports. 2016. link Times cited: 8 USED (low confidence) D. Terentyev, A. Zinovev, and G. Bonny, “Displacement cascades in FeNiMnCu alloys: RVP model alloys,” Journal of Nuclear Materials. 2016. link Times cited: 7 USED (low confidence) L. You, L. Hu, Y. Xie, and S. Zhao, “Influence of Cu precipitation on tensile properties of Fe–Cu–Ni ternary alloy at different temperatures by molecular dynamics simulation,” Computational Materials Science. 2016. link Times cited: 14 USED (low confidence) A. Al-Motasem, N. Mai, S. Choi, and M. Posselt, “Atomistic study on mixed-mode fracture mechanisms of ferrite iron interacting with coherent copper and nickel nanoclusters,” Journal of Nuclear Materials. 2016. link Times cited: 10 USED (low confidence) A. Nikonov, I. Konovalenko, and A. Dmitriev, “Molecular dynamics study of lattice rearrangement under mechanically activated diffusion,” Physical Mesomechanics. 2016. link Times cited: 35 USED (low confidence) G. Lv, H. Zhang, X. He, W. Yang, and Y. Su, “Vacancy enhanced formation and phase transition of Cu-rich precipitates in α - iron under neutron irradiation,” AIP Advances. 2016. link Times cited: 2 Abstract: In this paper, we employed both molecular statics and molecu… read more USED (low confidence) C. Liu, Z. Jiao, and J. Luan, “Copper-Rich Nanoclusters: Ferritic Steels Strengthened.” 2016. link Times cited: 3 USED (low confidence) A. Nikonov, I. Konovalenko, and A. Dmitriev, “Molecular dynamics study of lattice rearrangement under mechanically activated diffusion,” Physical Mesomechanics. 2016. link Times cited: 0 USED (low confidence) S. Shao, J. Wang, I. Beyerlein, and A. Misra, “Glide dislocation nucleation from dislocation nodes at semi-coherent 1 1 1 Cu–Ni interfaces,” Acta Materialia. 2015. link Times cited: 82 USED (low confidence) F. Z. Dai and W.-Z. Zhang, “An automatic and simple method for specifying dislocation features in atomistic simulations,” Comput. Phys. Commun. 2015. link Times cited: 26 USED (low confidence) F. Akasheh, M. R. Karim, and S. Shao, “Dislocation Structure of Cu/Nu (100) Semi-Coherent Interface and Its Role in Lattice Dislocation Nucleation.” 2015. link Times cited: 1 USED (low confidence) D. Terentyev, X. He, G. Bonny, A. Bakaev, E. Zhurkin, and L. Malerba, “Hardening due to dislocation loop damage in RPV model alloys: Role of Mn segregation,” Journal of Nuclear Materials. 2015. link Times cited: 36 USED (low confidence) Y. Qi, L. Wang, S. Wang, X. Li, and W. Cui, “Structural and dynamical heterogeneity of undercooled Fe75Cu25 melts with miscibility gap,” Journal of Alloys and Compounds. 2014. link Times cited: 11 USED (low confidence) C. Hu, M.-li Bai, J. Lv, H. Liu, and X.-jie Li, “Molecular dynamics investigation of the effect of copper nanoparticle on the solid contact between friction surfaces,” Applied Surface Science. 2014. link Times cited: 47 USED (low confidence) F. Bergner, A. Ulbricht, P. Lindner, U. Keiderling, and L. Malerba, “Post-irradiation annealing behavior of neutron-irradiated FeCu, FeMnNi and FeMnNiCu model alloys investigated by means of small-angle neutron scattering,” Journal of Nuclear Materials. 2014. link Times cited: 11 USED (low confidence) G. Bonny, D. Terentyev, E. Zhurkin, and L. Malerba, “Monte Carlo study of decorated dislocation loops in FeNiMnCu model alloys,” Journal of Nuclear Materials. 2014. link Times cited: 45 USED (low confidence) H. Morita and A. Takahashi, “Numerical analysis of interaction between solute atom and extended dislocation using force multipoles,” Journal of Central South University. 2014. link Times cited: 0 USED (low confidence) S. Shao, J. Wang, A. Misra, and R. Hoagland, “Relaxation of Misfit Dislocations at Nodes,” Materials Science Forum. 2014. link Times cited: 3 Abstract: Experimental studies proved that structures and properties o… read more USED (low confidence) B. Onat and S. Durukanoğlu, “An optimized interatomic potential for Cu–Ni alloys with the embedded-atom method,” Journal of Physics: Condensed Matter. 2014. link Times cited: 86 Abstract: We have developed a semi-empirical and many-body type model … read more USED (low confidence) G. Bonny et al., “On the thermal stability of late blooming phases in reactor pressure vessel steels: An atomistic study,” Journal of Nuclear Materials. 2013. link Times cited: 77 USED (low confidence) Z. Jiao, J. Luan, Z. Zhang, M. K. Miller, W. Ma, and C. Liu, “Synergistic effects of Cu and Ni on nanoscale precipitation and mechanical properties of high-strength steels,” Acta Materialia. 2013. link Times cited: 163 USED (low confidence) X. Shu et al., “Fe self-diffusion and Cu and Ni diffusion in bulk and grain boundary of Fe: A molecular dynamics study,” Nuclear Instruments & Methods in Physics Research Section B-beam Interactions With Materials and Atoms. 2013. link Times cited: 10 USED (low confidence) L. Shao et al., “Smoothing metallic glasses without introducing crystallization by gas cluster ion beam,” Applied Physics Letters. 2013. link Times cited: 13 Abstract: We show that 30 keV Ar cluster ion bombardment of Ni52.5Nb10… read more USED (low confidence) Y. Shim, N. Callahan, and J. Amar, “Localized saddle-point search and application to temperature-accelerated dynamics.,” The Journal of chemical physics. 2013. link Times cited: 9 Abstract: We present a method for speeding up temperature-accelerated … read more USED (low confidence) D. Molnár et al., “Multiscale simulations on the coarsening of Cu-rich precipitates in α-Fe using kinetic Monte Carlo, molecular dynamics and phase-field simulations,” Acta Materialia. 2012. link Times cited: 59 USED (low confidence) N. Gunkelmann, H. Ledbetter, and H. Urbassek, “Experimental and atomistic study of the elastic properties of α′ Fe–C martensite,” Acta Materialia. 2012. link Times cited: 38 USED (low confidence) D. Terentyev and L. Malerba, “Interaction of a screw dislocation with Cu-precipitates, nanovoids and Cu–vacancy clusters in BCC iron,” Journal of Nuclear Materials. 2012. link Times cited: 34 USED (low confidence) Y. Ashkenazy, N. Q. Vo, D. Schwen, R. Averback, and P. Bellon, “Shear induced chemical mixing in heterogeneous systems,” Acta Materialia. 2012. link Times cited: 108 USED (low confidence) D. Terentyev, L. Malerba, G. Bonny, A. Al-Motasem, and M. Posselt, “Interaction of an edge dislocation with Cu–Ni-vacancy clusters in bcc iron,” Journal of Nuclear Materials. 2011. link Times cited: 24 USED (low confidence) A. Al-Motasem, M. Posselt, and F. Bergner, “Nanoclusters in bcc-Fe containing vacancies, copper and nickel: Structure and energetics,” Journal of Nuclear Materials. 2011. link Times cited: 25 USED (low confidence) B. Jelinek et al., “Modified embedded atom method potential for Al, Si, Mg, Cu, and Fe alloys,” Physical Review B. 2011. link Times cited: 218 Abstract: A set of modified embedded-atom method (MEAM) potentials for… read more USED (low confidence) L. Malerba et al., “Comparison of empirical interatomic potentials for iron applied to radiation damage studies,” Journal of Nuclear Materials. 2010. link Times cited: 210 USED (low confidence) N. Castin, L. Malerba, G. Bonny, M. I. Pascuet, and M. Hou, “Modelling radiation-induced phase changes in binary FeCu and ternary FeCuNi alloys using an artificial intelligence-based atomistic kinetic Monte Carlo approach,” Nuclear Instruments & Methods in Physics Research Section B-beam Interactions With Materials and Atoms. 2009. link Times cited: 24 USED (low confidence) K. Chen et al., “Extra-ductile and strong tin bronze alloy via high-density intragranular ultra-nano precipitation with minimal lattice misfit,” Scripta Materialia. 2023. link Times cited: 0 USED (low confidence) F. Wang et al., “Atomic-scale simulations in multi-component alloys and compounds: A review on advances in interatomic potential,” Journal of Materials Science & Technology. 2023. link Times cited: 9 USED (low confidence) A. Nikonov and A. I. Dmitriev, “Molecular-dynamic calculation of the interaction parameters of meso-scale particles of dissimilar metals,” PHYSICAL MESOMECHANICS OF CONDENSED MATTER: Physical Principles of Multiscale Structure Formation and the Mechanisms of Nonlinear Behavior: MESO2022. 2023. link Times cited: 0 USED (low confidence) S. Eder, P. Grützmacher, M. R. Ripoll, C. Gachot, and D. Dini, “Does speed kill or make friction better?—Designing materials for high velocity sliding,” Applied Materials Today. 2022. link Times cited: 7 USED (low confidence) D. Mejía-Burgos, S. Berrios, J. Mazo‐Zuluaga, and J. Mejía‐López, “Structural stability, shape memory and mechanical properties of Fe/Ni core/shell nanorods,” Journal of Alloys and Compounds. 2021. link Times cited: 0 USED (low confidence) L. Malerba, “Large Scale Integrated Materials Modeling Programs.” 2020. link Times cited: 2 USED (low confidence) C. Becquart and F. Soisson, “Monte Carlo Simulations of Precipitation Under Irradiation,” Handbook of Mechanics of Materials. 2019. link Times cited: 7 USED (low confidence) D. Rapp et al., “Multiscale Simulation of Precipitation in Copper-Alloyed Pipeline Steels and in Cu-Ni-Si Alloys,” Handbook of Mechanics of Materials. 2019. link Times cited: 0 USED (low confidence) Ž. Božić, S. Schmauder, M. Mlikota, and M. Hummel, “Multiscale Fatigue Crack Growth Modeling for Welded Stiffened Panels,” Handbook of Mechanics of Materials. 2019. link Times cited: 3 USED (low confidence) S. Fazeli, M. Vahedpour, and S. Sadrnezhaad, “Effect of copper content on tensile mechanical properties of ternary NiTiCu alloy nanowire: Molecular dynamics simulation,” Materials Today: Proceedings. 2018. link Times cited: 4 USED (low confidence) K. Zolnikov, D. S. Kryzhevich, and A. Korchuganov, “Peculiarities of structural transformations in metal nanoparticles at high speed collisions,” Journal of Physics: Conference Series. 2018. link Times cited: 1 Abstract: A molecular dynamics simulation of nanosized particle collis… read more USED (low confidence) K. Zolnikov, D. Kryzhevich, E. Shilko, and A. Korchuganov, “Molecular Dynamics Simulation Of Electric Pulse Explosion Of Metal Wires,” Procedia structural integrity. 2016. link Times cited: 1 USED (low confidence) M. Hummel, A.-P. Prskalo, P. Binkele, and S. Schmauder, “MD-Simulations on Metallic Alloys,” International Conference on High Performance Computing. 2015. link Times cited: 1 USED (low confidence) D. Molnár, P. Binkele, A. Mora, R. Mukherjee, B. Nestler, and S. Schmauder, “Molecular Dynamics virtual testing of thermally aged Fe–Cu microstructures obtained from multiscale simulations,” Computational Materials Science. 2014. link Times cited: 9 USED (low confidence) I. Mastorakos, H. Zbib, D. Li, M. Khaleel, and X. Sun, “Multiscale Modeling of Irradiation Induced Hardening in Iron Alloys,” MRS Proceedings. 2012. link Times cited: 0 USED (low confidence) E. Lin, L. Niu, H.-ji Shi, and Z. Duan, “Molecular dynamics simulation of nano-scale interfacial friction characteristic for different tribopair systems,” Applied Surface Science. 2012. link Times cited: 26 USED (low confidence) L. Malerba, “Multi-scale modelling of irradiation effects in nuclear power plant materials.” 2010. link Times cited: 3 Abstract: Abstract: This chapter surveys the computer-based multi-scal… read more NOT USED (high confidence) G. Chu et al., “MD Simulation of Hundred-Billion-Metal-Atom Cascade Collision on Sunway Taihulight,” Comput. Phys. Commun. 2021. link Times cited: 7 NOT USED (high confidence) P. Yu, L. Zhang, and L. Du, “Atomic Simulations for Packing Changes of Nano-Sized Cu Clusters Embedded in the Febulk on Heating,” Metals. 2021. link Times cited: 3 Abstract: Understanding of the defect evolution mechanism under irradi… read more NOT USED (high confidence) B. Lin, J. Wang, J. Li, and Z. Wang, “A neural-network based framework of developing cross interaction in alloy embedded-atom method potentials: application to Zr–Nb alloy,” Journal of Physics: Condensed Matter. 2020. link Times cited: 2 Abstract: Interaction potentials are critical to molecular dynamics si… read more NOT USED (high confidence) S. Eder, M. R. Ripoll, U. Cihak-Bayr, D. Dini, and C. Gachot, “Unraveling and Mapping the Mechanisms for Near-surface Microstructure Evolution in CuNi Alloys under Sliding.,” ACS applied materials & interfaces. 2020. link Times cited: 30 Abstract: The origin of friction and wear in polycrystalline materials… read more NOT USED (high confidence) T. M. Whiting, P. Burr, D. King, and M. Wenman, “Understanding the importance of the energetics of Mn, Ni, Cu, Si and vacancy triplet clusters in bcc Fe,” Journal of Applied Physics. 2019. link Times cited: 11 Abstract: Numerous experimental studies have found the presence of (Cu… read more NOT USED (high confidence) S. Zhi-peng, D. Fuzhi, X. Ben, and Z. Wen-zheng, “Three-Dimensional Growth of Coherent Ferrite in Austenite: A Molecular Dynamics Study,” Acta Metallurgica Sinica (english Letters). 2019. link Times cited: 1 NOT USED (high confidence) X. Wu et al., “Softening effects due to reorientations of Cu precipitates in α-iron: Atomistic simulations of dislocations-obstacles interactions,” Journal of Applied Physics. 2019. link Times cited: 3 Abstract: Radiation-induced hardening by precipitates, which essential… read more NOT USED (high confidence) C. Hu, J. Lv, M.-li Bai, X. Zhang, and D. Tang, “Molecular dynamics simulation of effects of nanoparticles on frictional heating and tribological properties at various temperatures,” Friction. 2019. link Times cited: 26 NOT USED (high confidence) Z. Sun, F. Z. Dai, B. Xu, and W.-Z. Zhang, “Three-Dimensional Growth of Coherent Ferrite in Austenite: A Molecular Dynamics Study,” Acta Metallurgica Sinica (English Letters). 2019. link Times cited: 5 NOT USED (high confidence) S. Mahmoud and N. Mousseau, “Long-time point defect diffusion in ordered nickel-based binary alloys: How small kinetic differences can lead to completely long-time structural evolution,” Materialia. 2018. link Times cited: 15 NOT USED (high confidence) Y. Zhang, D. Schwen, and X. Bai, “Molecular dynamics simulations of concentration-dependent defect production in Fe-Cr and Fe-Cu alloys,” Journal of Applied Physics. 2017. link Times cited: 13 Abstract: Molecular dynamics simulations are conducted to study the ef… read more NOT USED (high confidence) B. Cheng and M. Ceriotti, “Computing the absolute Gibbs free energy in atomistic simulations: Applications to defects in solids,” Physical Review B. 2017. link Times cited: 40 Abstract: The Gibbs free energy is the fundamental thermodynamic poten… read more NOT USED (high confidence) K. Liu et al., “Effect of Ni and vacancy concentration on initial formation of Cu precipitate in Fe–Cu–Ni ternary alloys by molecular dynamics simulation,” Chinese Physics B. 2017. link Times cited: 5 NOT USED (high confidence) A. Akbarzadeh, Y. Cui, and Z. Chen, “Thermal wave: from nonlocal continuum to molecular dynamics,” RSC Advances. 2017. link Times cited: 24 Abstract: It is well known that the continuum model of Fourier's … read more NOT USED (high confidence) S. M. Rassoulinejad-Mousavi, Y. Mao, and Y. Zhang, “Evaluation of Copper, Aluminum and Nickel Interatomic Potentials on Predicting the Elastic Properties,” arXiv: Computational Physics. 2016. link Times cited: 63 Abstract: Choice of appropriate force field is one of the main concern… read more NOT USED (high confidence) I. Hijazi and Y. H. Park, “Mixed intermetallic potentials for Fe-Cu compounds,” Molecular Simulation. 2016. link Times cited: 0 Abstract: Metastable Fe-Cu alloys are of considerable scientific inter… read more NOT USED (high confidence) S. Parviainen, F. Djurabekova, S. Fitzgerald, A. Ruzibaev, and K. Nordlund, “Atomistic simulations of field assisted evaporation in atom probe tomography,” Journal of Physics D: Applied Physics. 2016. link Times cited: 19 Abstract: Atom probe tomography (APT) is an extremely powerful techniq… read more NOT USED (high confidence) C. Hu, M.-li Bai, J. Lv, Z. Kou, and X.-jie Li, “Molecular dynamics simulation on the tribology properties of two hard nanoparticles (diamond and silicon dioxide) confined by two iron blocks,” Tribology International. 2015. link Times cited: 46 NOT USED (high confidence) Z. Lu-shan and Z. Shi-jin, “Influence of Ni on Cu precipitation in Fe—Cu—Ni ternary alloy by an atomic study,” Chinese Physics B. 2014. link Times cited: 9 Abstract: The early aging Cu precipitations in Fe—3%Cu and Fe—3%Cu—4%N… read more NOT USED (high confidence) W. Song and S.-jin Zhao, “Spin polarization gives rise to Cu precipitation in Fe-matrix.,” Physical chemistry chemical physics : PCCP. 2014. link Times cited: 9 Abstract: This article tries to uncover the physical reason of Cu prec… read more NOT USED (high confidence) J. Amar, Y. Shim, and R. Deck, “Critical island size for a shape transition in strained Cu/Ni(100) islands,” Surface Science. 2013. link Times cited: 3 NOT USED (high confidence) Q.-dong Liu, J. Gu, and W.-qing Liu, “On the Role of Ni in Cu Precipitation in Multicomponent Steels,” Metallurgical and Materials Transactions A. 2013. link Times cited: 19 NOT USED (high confidence) Y. Shim and J. Amar, “Shape transitions in strained Cu islands on Ni(100): kinetics versus energetics.,” Physical review letters. 2012. link Times cited: 7 Abstract: We examine the ramified islands observed in submonolayer Cu/… read more NOT USED (high confidence) L. Malerba et al., “Ab initio calculations and interatomic potentials for iron and iron alloys : Achievements within the Perfect Project,” Journal of Nuclear Materials. 2010. link Times cited: 65 NOT USED (high confidence) G. Bonny and R. Pasianot, “Gauge transformations to combine multi-component many-body interatomic potentials,” Philosophical Magazine Letters. 2010. link Times cited: 19 Abstract: Many-body interatomic potentials play an important role in a… read more NOT USED (high confidence) N. Castin and L. Malerba, “Calculation of proper energy barriers for atomistic kinetic Monte Carlo simulations on rigid lattice with chemical and strain field long-range effects using artificial neural networks.,” The Journal of chemical physics. 2010. link Times cited: 49 Abstract: In this paper we take a few steps further in the development… read more NOT USED (high confidence) C. Galvin, R. Grimes, and P. Burr, “A molecular dynamics method to identify the liquidus and solidus in a binary phase diagram,” Computational Materials Science. 2021. link Times cited: 6 NOT USED (high confidence) C. Becquart, N. Mousseau, and C. Domain, “Kinetic Monte Carlo Simulations of Irradiation Effects,” Comprehensive Nuclear Materials. 2020. link Times cited: 16 NOT USED (high confidence) B. Cheng, “Predicting homogeneous nucleation rate from atomistic simulations.” 2019. link Times cited: 0 Abstract: Nucleation is ubiquitous, from the formation of clouds to th… read more NOT USED (high confidence) J. S. Gibson, S. G. Srinivasan, M. Baskes, R. E. Miller, and A. K. Wilson, “A multi-state modified embedded atom method potential for titanium,” Modelling and Simulation in Materials Science and Engineering. 2016. link Times cited: 3 Abstract: The continuing search for broadly applicable, predictive, an… read more NOT USED (definite) Ž. Božić, S. Schmauder, M. Mlikota, and M. Hummel, “Multiscale fatigue crack growth modelling for welded stiffened panels,” Fatigue & Fracture of Engineering Materials & Structures. 2014. link Times cited: 72 Abstract: The influence of welding residual stresses in stiffened pane… read more |
| Funding | Not available |
| Short KIM ID
The unique KIM identifier code.
| MO_469343973171_005 |
| Extended KIM ID
The long form of the KIM ID including a human readable prefix (100 characters max), two underscores, and the Short KIM ID. Extended KIM IDs can only contain alpha-numeric characters (letters and digits) and underscores and must begin with a letter.
| EAM_Dynamo_BonnyPasianotCastin_2009_FeCuNi__MO_469343973171_005 |
| DOI |
10.25950/23db26d9 https://doi.org/10.25950/23db26d9 https://commons.datacite.org/doi.org/10.25950/23db26d9 |
| KIM Item Type
Specifies whether this is a Portable Model (software implementation of an interatomic model); Portable Model with parameter file (parameter file to be read in by a Model Driver); Model Driver (software implementation of an interatomic model that reads in parameters).
| Portable Model using Model Driver EAM_Dynamo__MD_120291908751_005 |
| Driver | EAM_Dynamo__MD_120291908751_005 |
| KIM API Version | 2.0 |
| Potential Type | eam |
| Previous Version | EAM_Dynamo_BonnyPasianotCastin_2009_FeCuNi__MO_469343973171_004 |
| Grade | Name | Category | Brief Description | Full Results | Aux File(s) |
|---|---|---|---|---|---|
| P | vc-species-supported-as-stated | mandatory | The model supports all species it claims to support; see full description. |
Results | Files |
| P | vc-periodicity-support | mandatory | Periodic boundary conditions are handled correctly; see full description. |
Results | Files |
| P | vc-permutation-symmetry | mandatory | Total energy and forces are unchanged when swapping atoms of the same species; see full description. |
Results | Files |
| B | vc-forces-numerical-derivative | consistency | Forces computed by the model agree with numerical derivatives of the energy; see full description. |
Results | Files |
| F | vc-dimer-continuity-c1 | informational | The energy versus separation relation of a pair of atoms is C1 continuous (i.e. the function and its first derivative are continuous); see full description. |
Results | Files |
| P | vc-objectivity | informational | Total energy is unchanged and forces transform correctly under rigid-body translation and rotation; see full description. |
Results | Files |
| P | vc-inversion-symmetry | informational | Total energy is unchanged and forces change sign when inverting a configuration through the origin; see full description. |
Results | Files |
| N/A | vc-memory-leak | informational | The model code does not have memory leaks (i.e. it releases all allocated memory at the end); see full description. |
Results | Files |
| P | vc-thread-safe | mandatory | The model returns the same energy and forces when computed in serial and when using parallel threads for a set of configurations. Note that this is not a guarantee of thread safety; see full description. |
Results | Files |
| P | vc-unit-conversion | mandatory | The model is able to correctly convert its energy and/or forces to different unit sets; see full description. |
Results | Files |
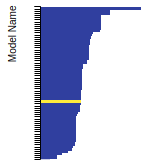
BCC Lattice Constant
This bar chart plot shows the mono-atomic body-centered cubic (bcc) lattice constant predicted by the current model (shown in the unique color) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
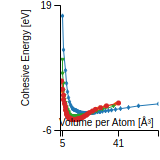
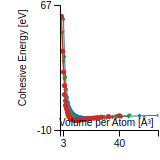
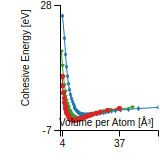
Cohesive Energy Graph
This graph shows the cohesive energy versus volume-per-atom for the current mode for four mono-atomic cubic phases (body-centered cubic (bcc), face-centered cubic (fcc), simple cubic (sc), and diamond). The curve with the lowest minimum is the ground state of the crystal if stable. (The crystal structure is enforced in these calculations, so the phase may not be stable.) Graphs are generated for each species supported by the model.
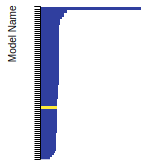
Diamond Lattice Constant
This bar chart plot shows the mono-atomic face-centered diamond lattice constant predicted by the current model (shown in the unique color) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
Dislocation Core Energies
This graph shows the dislocation core energy of a cubic crystal at zero temperature and pressure for a specific set of dislocation core cutoff radii. After obtaining the total energy of the system from conjugate gradient minimizations, non-singular, isotropic and anisotropic elasticity are applied to obtain the dislocation core energy for each of these supercells with different dipole distances. Graphs are generated for each species supported by the model.
(No matching species)FCC Elastic Constants
This bar chart plot shows the mono-atomic face-centered cubic (fcc) elastic constants predicted by the current model (shown in blue) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
FCC Lattice Constant
This bar chart plot shows the mono-atomic face-centered cubic (fcc) lattice constant predicted by the current model (shown in red) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
FCC Stacking Fault Energies
This bar chart plot shows the intrinsic and extrinsic stacking fault energies as well as the unstable stacking and unstable twinning energies for face-centered cubic (fcc) predicted by the current model (shown in blue) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
FCC Surface Energies
This bar chart plot shows the mono-atomic face-centered cubic (fcc) relaxed surface energies predicted by the current model (shown in blue) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
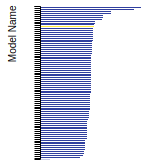
SC Lattice Constant
This bar chart plot shows the mono-atomic simple cubic (sc) lattice constant predicted by the current model (shown in the unique color) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
Cubic Crystal Basic Properties Table
Species: CuSpecies: Fe
Species: Ni
Disclaimer From Model Developer
The potential is stiffened.
Creators:
Contributor: karls
Publication Year: 2019
DOI: https://doi.org/10.25950/64cb38c5
This Test Driver uses LAMMPS to compute the cohesive energy of a given monoatomic cubic lattice (fcc, bcc, sc, or diamond) at a variety of lattice spacings. The lattice spacings range from a_min (=a_min_frac*a_0) to a_max (=a_max_frac*a_0) where a_0, a_min_frac, and a_max_frac are read from stdin (a_0 is typically approximately equal to the equilibrium lattice constant). The precise scaling and number of lattice spacings sampled between a_min and a_0 (a_0 and a_max) is specified by two additional parameters passed from stdin: N_lower and samplespacing_lower (N_upper and samplespacing_upper). Please see README.txt for further details.
Creators:
Contributor: ilia
Publication Year: 2024
DOI: https://doi.org/10.25950/888f9943
Computes the elastic constants for an arbitrary crystal. A robust computational protocol is used, attempting multiple methods and step sizes to achieve an acceptably low error in numerical differentiation and deviation from material symmetry. The crystal structure is specified using the AFLOW prototype designation as part of the Crystal Genome testing framework. In addition, the distance from the obtained elasticity tensor to the nearest isotropic tensor is computed.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Elastic constants for FeNi in AFLOW crystal prototype A2B_cF24_227_c_b at zero temperature and pressure v000 | view | 123282 |
Creators: Junhao Li and Ellad Tadmor
Contributor: tadmor
Publication Year: 2019
DOI: https://doi.org/10.25950/5853fb8f
Computes the cubic elastic constants for some common crystal types (fcc, bcc, sc, diamond) by calculating the hessian of the energy density with respect to strain. An estimate of the error associated with the numerical differentiation performed is reported.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Elastic constants for bcc Cu at zero temperature v006 | view | 1791 | |
| Elastic constants for bcc Fe at zero temperature v006 | view | 1983 | |
| Elastic constants for bcc Ni at zero temperature v006 | view | 1919 | |
| Elastic constants for fcc Cu at zero temperature v006 | view | 2047 | |
| Elastic constants for fcc Fe at zero temperature v006 | view | 2079 | |
| Elastic constants for fcc Ni at zero temperature v006 | view | 1919 | |
| Elastic constants for sc Cu at zero temperature v006 | view | 6174 | |
| Elastic constants for sc Fe at zero temperature v006 | view | 3807 | |
| Elastic constants for sc Ni at zero temperature v006 | view | 1823 |
Creators: Junhao Li
Contributor: jl2922
Publication Year: 2019
DOI: https://doi.org/10.25950/d794c746
Computes the elastic constants for hcp crystals by calculating the hessian of the energy density with respect to strain. An estimate of the error associated with the numerical differentiation performed is reported.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Elastic constants for hcp Cu at zero temperature v004 | view | 1783 | |
| Elastic constants for hcp Fe at zero temperature v004 | view | 2388 | |
| Elastic constants for hcp Ni at zero temperature v004 | view | 2133 |
Creators:
Contributor: ilia
Publication Year: 2023
DOI: https://doi.org/10.25950/e8a7ed84
Computes the equilibrium crystal structure and energy for an arbitrary crystal at zero temperature and applied stress by performing symmetry-constrained relaxation. The crystal structure is specified using the AFLOW prototype designation. Multiple sets of free parameters corresponding to the crystal prototype may be specified as initial guesses for structure optimization. No guarantee is made regarding the stability of computed equilibria, nor that any are the ground state.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Equilibrium crystal structure and energy for Cu in AFLOW crystal prototype A_cF4_225_a v001 | view | 61915 | |
| Equilibrium crystal structure and energy for Cu in AFLOW crystal prototype A_cI2_229_a v001 | view | 68393 |
Creators:
Contributor: ilia
Publication Year: 2024
DOI: https://doi.org/10.25950/2f2c4ad3
Computes the equilibrium crystal structure and energy for an arbitrary crystal at zero temperature and applied stress by performing symmetry-constrained relaxation. The crystal structure is specified using the AFLOW prototype designation. Multiple sets of free parameters corresponding to the crystal prototype may be specified as initial guesses for structure optimization. No guarantee is made regarding the stability of computed equilibria, nor that any are the ground state.
Creators:
Contributor: brunnels
Publication Year: 2022
DOI: https://doi.org/10.25950/2c59c9d6
Computes grain boundary energy for a range of tilt angles given a crystal structure, tilt axis, and material.
Creators: Daniel S. Karls and Junhao Li
Contributor: karls
Publication Year: 2019
DOI: https://doi.org/10.25950/2765e3bf
Equilibrium lattice constant and cohesive energy of a cubic lattice at zero temperature and pressure.
Creators: Daniel S. Karls and Junhao Li
Contributor: karls
Publication Year: 2019
DOI: https://doi.org/10.25950/c339ca32
Calculates lattice constant of hexagonal bulk structures at zero temperature and pressure by using simplex minimization to minimize the potential energy.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Equilibrium lattice constants for hcp Cu v005 | view | 30467 | |
| Equilibrium lattice constants for hcp Fe v005 | view | 27825 | |
| Equilibrium lattice constants for hcp Ni v005 | view | 20502 |
Creators: Mingjian Wen
Contributor: mjwen
Publication Year: 2019
DOI: https://doi.org/10.25950/fc69d82d
This Test Driver uses LAMMPS to compute the linear thermal expansion coefficient at a finite temperature under a given pressure for a cubic lattice (fcc, bcc, sc, diamond) of a single given species.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Linear thermal expansion coefficient of fcc Cu at 293.15 K under a pressure of 0 MPa v001 | view | 7039339 |
Creators:
Contributor: mjwen
Publication Year: 2024
DOI: https://doi.org/10.25950/9d9822ec
This Test Driver uses LAMMPS to compute the linear thermal expansion coefficient at a finite temperature under a given pressure for a cubic lattice (fcc, bcc, sc, diamond) of a single given species.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Linear thermal expansion coefficient of bcc Fe at 293.15 K under a pressure of 0 MPa v002 | view | 378596 | |
| Linear thermal expansion coefficient of fcc Ni at 293.15 K under a pressure of 0 MPa v002 | view | 638345 |
Creators: Matt Bierbaum
Contributor: mattbierbaum
Publication Year: 2019
DOI: https://doi.org/10.25950/64f4999b
Calculates the phonon dispersion relations for fcc lattices and records the results as curves.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Phonon dispersion relations for fcc Cu v004 | view | 52910 | |
| Phonon dispersion relations for fcc Ni v004 | view | 49743 |
Creators:
Contributor: SubrahmanyamPattamatta
Publication Year: 2019
DOI: https://doi.org/10.25950/b4cfaf9a
Intrinsic and extrinsic stacking fault energies, unstable stacking fault energy, unstable twinning energy, stacking fault energy as a function of fractional displacement, and gamma surface for a monoatomic FCC lattice at zero temperature and pressure.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Stacking and twinning fault energies for fcc Cu v002 | view | 5708341 | |
| Stacking and twinning fault energies for fcc Ni v002 | view | 6224548 |
Creators: Matt Bierbaum
Contributor: mattbierbaum
Publication Year: 2019
DOI: https://doi.org/10.25950/6c43a4e6
Calculates the surface energy of several high symmetry surfaces and produces a broken-bond model fit. In latex form, the fit equations are given by:
E_{FCC} (\vec{n}) = p_1 (4 \left( |x+y| + |x-y| + |x+z| + |x-z| + |z+y| +|z-y|\right)) + p_2 (8 \left( |x| + |y| + |z|\right)) + p_3 (2 ( |x+ 2y + z| + |x+2y-z| + |x-2y + z| + |x-2y-z| + |2x+y+z| + |2x+y-z| +|2x-y+z| +|2x-y-z| +|x+y+2z| +|x+y-2z| +|x-y+2z| +|x-y-2z| ) + c
E_{BCC} (\vec{n}) = p_1 (6 \left( | x+y+z| + |x+y-z| + |-x+y-z| + |x-y+z| \right)) + p_2 (8 \left( |x| + |y| + |z|\right)) + p_3 (4 \left( |x+y| + |x-y| + |x+z| + |x-z| + |z+y| +|z-y|\right)) +c.
In Python, these two fits take the following form:
def BrokenBondFCC(params, index):
import numpy
x, y, z = index
x = x / numpy.sqrt(x**2.+y**2.+z**2.)
y = y / numpy.sqrt(x**2.+y**2.+z**2.)
z = z / numpy.sqrt(x**2.+y**2.+z**2.)
return params[0]*4* (abs(x+y) + abs(x-y) + abs(x+z) + abs(x-z) + abs(z+y) + abs(z-y)) + params[1]*8*(abs(x) + abs(y) + abs(z)) + params[2]*(abs(x+2*y+z) + abs(x+2*y-z) +abs(x-2*y+z) +abs(x-2*y-z) + abs(2*x+y+z) +abs(2*x+y-z) +abs(2*x-y+z) +abs(2*x-y-z) + abs(x+y+2*z) +abs(x+y-2*z) +abs(x-y+2*z) +abs(x-y-2*z))+params[3]
def BrokenBondBCC(params, x, y, z):
import numpy
x, y, z = index
x = x / numpy.sqrt(x**2.+y**2.+z**2.)
y = y / numpy.sqrt(x**2.+y**2.+z**2.)
z = z / numpy.sqrt(x**2.+y**2.+z**2.)
return params[0]*6*(abs(x+y+z) + abs(x-y-z) + abs(x-y+z) + abs(x+y-z)) + params[1]*8*(abs(x) + abs(y) + abs(z)) + params[2]*4* (abs(x+y) + abs(x-y) + abs(x+z) + abs(x-z) + abs(z+y) + abs(z-y)) + params[3]
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Broken-bond fit of high-symmetry surface energies in bcc Fe v004 | view | 16858 | |
| Broken-bond fit of high-symmetry surface energies in fcc Cu v004 | view | 27511 | |
| Broken-bond fit of high-symmetry surface energies in fcc Ni v004 | view | 31477 |
Creators:
Contributor: efuem
Publication Year: 2023
DOI: https://doi.org/10.25950/fca89cea
Computes the monovacancy formation energy and relaxation volume for cubic and hcp monoatomic crystals.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Monovacancy formation energy and relaxation volume for bcc Fe | view | 393060 | |
| Monovacancy formation energy and relaxation volume for fcc Cu | view | 328347 | |
| Monovacancy formation energy and relaxation volume for fcc Ni | view | 391219 |
Creators:
Contributor: efuem
Publication Year: 2023
DOI: https://doi.org/10.25950/c27ba3cd
Computes the monovacancy formation and migration energies for cubic and hcp monoatomic crystals.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Vacancy formation and migration energy for bcc Fe | view | 3371966 | |
| Vacancy formation and migration energy for fcc Cu | view | 2058724 | |
| Vacancy formation and migration energy for fcc Ni | view | 1972809 |
| Test | Error Categories | Link to Error page |
|---|---|---|
| Elastic constants for diamond Cu at zero temperature v001 | other | view |
| Elastic constants for diamond Fe at zero temperature v001 | other | view |
| Elastic constants for diamond Ni at zero temperature v001 | other | view |
EquilibriumCrystalStructure__TD_457028483760_002
| Test | Error Categories | Link to Error page |
|---|---|---|
| Equilibrium crystal structure and energy for Fe in AFLOW crystal prototype A_tP1_123_a v002 | other | view |
LatticeConstantCubicEnergy__TD_475411767977_006
| Test | Error Categories | Link to Error page |
|---|---|---|
| Equilibrium zero-temperature lattice constant for diamond Cu | other | view |
| Equilibrium zero-temperature lattice constant for diamond Fe | other | view |
| Equilibrium zero-temperature lattice constant for diamond Ni | other | view |
No Driver
| Verification Check | Error Categories | Link to Error page |
|---|---|---|
| MemoryLeak__VC_561022993723_004 | other | view |
| EAM_Dynamo_BonnyPasianotCastin_2009_FeCuNi__MO_469343973171_005.txz | Tar+XZ | Linux and OS X archive |
| EAM_Dynamo_BonnyPasianotCastin_2009_FeCuNi__MO_469343973171_005.zip | Zip | Windows archive |
This Model requires a Model Driver. Archives for the Model Driver EAM_Dynamo__MD_120291908751_005 appear below.
| EAM_Dynamo__MD_120291908751_005.txz | Tar+XZ | Linux and OS X archive |
| EAM_Dynamo__MD_120291908751_005.zip | Zip | Windows archive |
The Fe-Fe interactions in this potential are based upon those of EAM_Dynamo_MendelevHanSrolovitz_2003Potential2_Fe__MO_769582363439_005 and are identical to those of EAM_Dynamo_BonnyPasianotMalerba_2009_FeNi__MO_267721408934_005. However, as Bonny et al. point out, there are two transformations in the EAM paradigm that leave the total energy invariant:
where
The values of these constants used by the authors to modify EAM_Dynamo_MendelevHanSrolovitz_2003Potential2_Fe__MO_769582363439_005 to describe interactions in pure Fe are
[1] Voter A F and Chen S P, Mater. Res. Soc. Symp. Proc. 82 (1987), pp. 175.
[2] Y. Mishin, M.J. Mehl, D.A. Papaconstantopoulos, A.F. Voter and J.D. Kress, Phys. Rev. B 63 (2001) p.224106.
Login to edit Wiki content