Tersoff_LAMMPS_ByggmastarNagelAlbe_2019_FeO__MO_608695023236_000
Tersoff_LAMMPS_ByggmastarNagelAlbe_2019_FeO__MO_608695023236_000
| Title
A single sentence description.
|
Tersoff-ZBL potential for FeO developed by Byggmastar et al. (2019) v000 |
|---|---|
| Description
A short description of the Model describing its key features including for example: type of model (pair potential, 3-body potential, EAM, etc.), modeled species (Ac, Ag, ..., Zr), intended purpose, origin, and so on.
|
This is an analytical bond-order potential for the Fe–O system, capable of reproducing the basic properties of wustite as well as the energetics of oxygen impurities in alpha-iron. The potential predicts binding energies of various small oxygen-vacancy clusters in alpha-iron in good agreement with density functional theory results, and is therefore suitable for simulations of oxygen-based defects in iron. The potential is not suitable for simulations of the Fe2O3 and Fe3O4 phases. |
| Species
The supported atomic species.
| Fe, O |
| Disclaimer
A statement of applicability provided by the contributor, informing users of the intended use of this KIM Item.
|
None |
| Content Origin | https://www.ctcms.nist.gov/potentials/entry/2019--Byggmastar-J-Nagel-M-Albe-K-et-al--Fe-O/ |
| Contributor |
I Nikiforov |
| Maintainer |
I Nikiforov |
| Developer |
Jesper Byggmästar Morten Nagel Karsten Albe Krister O. E. Henriksson Kai Nordlund |
| Published on KIM | 2022 |
| How to Cite |
This Model originally published in [1] is archived in OpenKIM [2-5]. [1] Byggmästar J, Nagel M, Albe K, Henriksson KOE, Nordlund K. Analytical interatomic bond-order potential for simulations of oxygen defects in iron. Journal of Physics: Condensed Matter [Internet]. 2019Mar;31(21):215401. Available from: https://doi.org/10.1088/1361-648x/ab0931 doi:10.1088/1361-648x/ab0931 — (Primary Source) A primary source is a reference directly related to the item documenting its development, as opposed to other sources that are provided as background information. [2] Byggmästar J, Nagel M, Albe K, Henriksson KOE, Nordlund K. Tersoff-ZBL potential for FeO developed by Byggmastar et al. (2019) v000. OpenKIM; 2022. doi:10.25950/dc7b5aa7 [3] Brink T, Thompson AP, Farrell DE, Wen M, Tersoff J, Nord J, et al. Model driver for Tersoff-style potentials ported from LAMMPS v005. OpenKIM; 2021. doi:10.25950/9a7dc96c [4] Tadmor EB, Elliott RS, Sethna JP, Miller RE, Becker CA. The potential of atomistic simulations and the Knowledgebase of Interatomic Models. JOM. 2011;63(7):17. doi:10.1007/s11837-011-0102-6 [5] Elliott RS, Tadmor EB. Knowledgebase of Interatomic Models (KIM) Application Programming Interface (API). OpenKIM; 2011. doi:10.25950/ff8f563a Click here to download the above citation in BibTeX format. |
| Citations
This panel presents information regarding the papers that have cited the interatomic potential (IP) whose page you are on. The OpenKIM machine learning based Deep Citation framework is used to determine whether the citing article actually used the IP in computations (denoted by "USED") or only provides it as a background citation (denoted by "NOT USED"). For more details on Deep Citation and how to work with this panel, click the documentation link at the top of the panel. The word cloud to the right is generated from the abstracts of IP principle source(s) (given below in "How to Cite") and the citing articles that were determined to have used the IP in order to provide users with a quick sense of the types of physical phenomena to which this IP is applied. The bar chart shows the number of articles that cited the IP per year. Each bar is divided into green (articles that USED the IP) and blue (articles that did NOT USE the IP). Users are encouraged to correct Deep Citation errors in determination by clicking the speech icon next to a citing article and providing updated information. This will be integrated into the next Deep Citation learning cycle, which occurs on a regular basis. OpenKIM acknowledges the support of the Allen Institute for AI through the Semantic Scholar project for providing citation information and full text of articles when available, which are used to train the Deep Citation ML algorithm. |
This panel provides information on past usage of this interatomic potential (IP) powered by the OpenKIM Deep Citation framework. The word cloud indicates typical applications of the potential. The bar chart shows citations per year of this IP (bars are divided into articles that used the IP (green) and those that did not (blue)). The complete list of articles that cited this IP is provided below along with the Deep Citation determination on usage. See the Deep Citation documentation for more information. 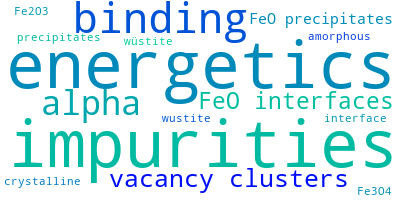
10 Citations (6 used)
Help us to determine which of the papers that cite this potential actually used it to perform calculations. If you know, click the .
USED (low confidence) N. Fominykh, V. Nikolskiy, and V. Stegailov, “Atomistic model of an oxide film in contact with a liquid metal coolant: Defects concentrations and chemical potentials of dissolved Fe–O,” Computational Materials Science. 2023. link Times cited: 5 USED (low confidence) M. Fan, C. Zhou, J. Duan, J. Gong, and Z.-yi Jiang, “Effect of indentation rate on deformation behavior and mechanical properties of FeO/Fe is simulated based on molecular dynamics,” Applied Physics A. 2023. link Times cited: 0 USED (low confidence) Z. Zhang et al., “A force field for molecular dynamics simulations of iron oxide system,” Materials Science and Engineering: B. 2022. link Times cited: 0 USED (low confidence) E. Hodille, J. Byggmästar, Y. Ferro, and K. Nordlund, “Molecular dynamics study of hydrogen isotopes at the Be/BeO interface,” Journal of Physics: Condensed Matter. 2022. link Times cited: 3 Abstract: Molecular dynamics simulations are used to investigate the b… read more USED (low confidence) Z. E. Oufir, H. Ramézani, N. Mathieu, S. Delpeux, and S. Bhatia, “Influence of force field used in carbon nanostructure reconstruction on simulated phenol adsorption isotherms in aqueous medium,” Journal of Molecular Liquids. 2021. link Times cited: 2 USED (low confidence) L. Yang, W. Zhang, L. He, H. Li, and S.-bo Zheng, “Study on the growth and morphology evolution of titanium oxide clusters in molten iron with molecular dynamics simulation,” RSC Advances. 2019. link Times cited: 5 Abstract: Formation of nano-scale titanium oxides is a desirable resul… read more NOT USED (low confidence) Y.-F. Wu, W. Yu, and S. Shen, “Developing an analytical bond-order potential for Hf/Nb/Ta/Zr/C system using machine learning global optimization,” Ceramics International. 2023. link Times cited: 0 NOT USED (low confidence) Y. Lei et al., “An Embedded-Atom Method Potential for studying the properties of Fe-Pb solid-liquid interface,” Journal of Nuclear Materials. 2022. link Times cited: 1 NOT USED (high confidence) B. Waters, D. S. Karls, I. Nikiforov, R. Elliott, E. Tadmor, and B. Runnels, “Automated determination of grain boundary energy and potential-dependence using the OpenKIM framework,” Computational Materials Science. 2022. link Times cited: 5 |
| Funding |
Award Number: 259249 Funder: Academy of Finland Award Number: 633053 Funder: H2020 Euratom |
| Short KIM ID
The unique KIM identifier code.
| MO_608695023236_000 |
| Extended KIM ID
The long form of the KIM ID including a human readable prefix (100 characters max), two underscores, and the Short KIM ID. Extended KIM IDs can only contain alpha-numeric characters (letters and digits) and underscores and must begin with a letter.
| Tersoff_LAMMPS_ByggmastarNagelAlbe_2019_FeO__MO_608695023236_000 |
| DOI |
10.25950/dc7b5aa7 https://doi.org/10.25950/dc7b5aa7 https://commons.datacite.org/doi.org/10.25950/dc7b5aa7 |
| KIM Item Type
Specifies whether this is a Portable Model (software implementation of an interatomic model); Portable Model with parameter file (parameter file to be read in by a Model Driver); Model Driver (software implementation of an interatomic model that reads in parameters).
| Portable Model using Model Driver Tersoff_LAMMPS__MD_077075034781_005 |
| Driver | Tersoff_LAMMPS__MD_077075034781_005 |
| KIM API Version | 2.2 |
| Potential Type | tersoff |
| Grade | Name | Category | Brief Description | Full Results | Aux File(s) |
|---|---|---|---|---|---|
| P | vc-species-supported-as-stated | mandatory | The model supports all species it claims to support; see full description. |
Results | Files |
| P | vc-periodicity-support | mandatory | Periodic boundary conditions are handled correctly; see full description. |
Results | Files |
| P | vc-permutation-symmetry | mandatory | Total energy and forces are unchanged when swapping atoms of the same species; see full description. |
Results | Files |
| A | vc-forces-numerical-derivative | consistency | Forces computed by the model agree with numerical derivatives of the energy; see full description. |
Results | Files |
| F | vc-dimer-continuity-c1 | informational | The energy versus separation relation of a pair of atoms is C1 continuous (i.e. the function and its first derivative are continuous); see full description. |
Results | Files |
| P | vc-objectivity | informational | Total energy is unchanged and forces transform correctly under rigid-body translation and rotation; see full description. |
Results | Files |
| P | vc-inversion-symmetry | informational | Total energy is unchanged and forces change sign when inverting a configuration through the origin; see full description. |
Results | Files |
| P | vc-memory-leak | informational | The model code does not have memory leaks (i.e. it releases all allocated memory at the end); see full description. |
Results | Files |
| P | vc-thread-safe | mandatory | The model returns the same energy and forces when computed in serial and when using parallel threads for a set of configurations. Note that this is not a guarantee of thread safety; see full description. |
Results | Files |
| N/A | vc-unit-conversion | mandatory | The model is able to correctly convert its energy and/or forces to different unit sets; see full description. |
Results | Files |
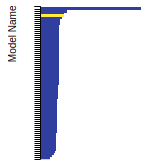
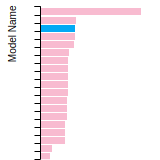
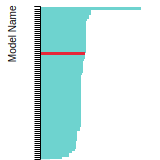
BCC Lattice Constant
This bar chart plot shows the mono-atomic body-centered cubic (bcc) lattice constant predicted by the current model (shown in the unique color) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
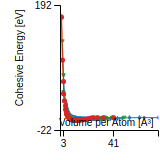
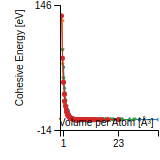
Cohesive Energy Graph
This graph shows the cohesive energy versus volume-per-atom for the current mode for four mono-atomic cubic phases (body-centered cubic (bcc), face-centered cubic (fcc), simple cubic (sc), and diamond). The curve with the lowest minimum is the ground state of the crystal if stable. (The crystal structure is enforced in these calculations, so the phase may not be stable.) Graphs are generated for each species supported by the model.
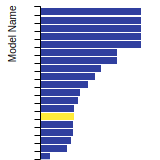
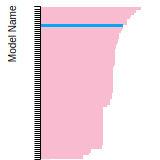
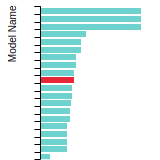
Diamond Lattice Constant
This bar chart plot shows the mono-atomic face-centered diamond lattice constant predicted by the current model (shown in the unique color) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
Dislocation Core Energies
This graph shows the dislocation core energy of a cubic crystal at zero temperature and pressure for a specific set of dislocation core cutoff radii. After obtaining the total energy of the system from conjugate gradient minimizations, non-singular, isotropic and anisotropic elasticity are applied to obtain the dislocation core energy for each of these supercells with different dipole distances. Graphs are generated for each species supported by the model.
(No matching species)FCC Elastic Constants
This bar chart plot shows the mono-atomic face-centered cubic (fcc) elastic constants predicted by the current model (shown in blue) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
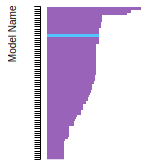
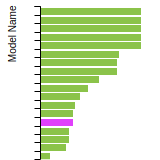
FCC Lattice Constant
This bar chart plot shows the mono-atomic face-centered cubic (fcc) lattice constant predicted by the current model (shown in red) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
FCC Stacking Fault Energies
This bar chart plot shows the intrinsic and extrinsic stacking fault energies as well as the unstable stacking and unstable twinning energies for face-centered cubic (fcc) predicted by the current model (shown in blue) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
(No matching species)FCC Surface Energies
This bar chart plot shows the mono-atomic face-centered cubic (fcc) relaxed surface energies predicted by the current model (shown in blue) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
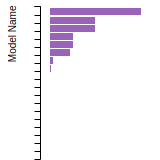
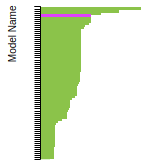
(No matching species)SC Lattice Constant
This bar chart plot shows the mono-atomic simple cubic (sc) lattice constant predicted by the current model (shown in the unique color) compared with the predictions for all other models in the OpenKIM Repository that support the species. The vertical bars show the average and standard deviation (one sigma) bounds for all model predictions. Graphs are generated for each species supported by the model.
Cubic Crystal Basic Properties Table
Species: FeSpecies: O
Creators:
Contributor: karls
Publication Year: 2019
DOI: https://doi.org/10.25950/64cb38c5
This Test Driver uses LAMMPS to compute the cohesive energy of a given monoatomic cubic lattice (fcc, bcc, sc, or diamond) at a variety of lattice spacings. The lattice spacings range from a_min (=a_min_frac*a_0) to a_max (=a_max_frac*a_0) where a_0, a_min_frac, and a_max_frac are read from stdin (a_0 is typically approximately equal to the equilibrium lattice constant). The precise scaling and number of lattice spacings sampled between a_min and a_0 (a_0 and a_max) is specified by two additional parameters passed from stdin: N_lower and samplespacing_lower (N_upper and samplespacing_upper). Please see README.txt for further details.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Cohesive energy versus lattice constant curve for bcc Fe v004 | view | 2298 | |
| Cohesive energy versus lattice constant curve for bcc O v004 | view | 2616 | |
| Cohesive energy versus lattice constant curve for diamond Fe v004 | view | 2337 | |
| Cohesive energy versus lattice constant curve for diamond O v004 | view | 2650 | |
| Cohesive energy versus lattice constant curve for fcc Fe v004 | view | 2870 | |
| Cohesive energy versus lattice constant curve for fcc O v004 | view | 2805 | |
| Cohesive energy versus lattice constant curve for sc Fe v004 | view | 2348 | |
| Cohesive energy versus lattice constant curve for sc O v004 | view | 2695 |
Creators:
Contributor: ilia
Publication Year: 2024
DOI: https://doi.org/10.25950/888f9943
Computes the elastic constants for an arbitrary crystal. A robust computational protocol is used, attempting multiple methods and step sizes to achieve an acceptably low error in numerical differentiation and deviation from material symmetry. The crystal structure is specified using the AFLOW prototype designation as part of the Crystal Genome testing framework. In addition, the distance from the obtained elasticity tensor to the nearest isotropic tensor is computed.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Elastic constants for FeO in AFLOW crystal prototype A2B3_cI80_206_ad_e at zero temperature and pressure v000 | view | 283992 | |
| Elastic constants for FeO in AFLOW crystal prototype A2B3_hR10_167_c_e at zero temperature and pressure v000 | view | 244273 | |
| Elastic constants for FeO in AFLOW crystal prototype A2B3_oC20_63_ac_cf at zero temperature and pressure v000 | view | 107059 | |
| Elastic constants for FeO in AFLOW crystal prototype A2B3_oP20_60_d_cd at zero temperature and pressure v000 | view | 427325 | |
| Elastic constants for FeO in AFLOW crystal prototype A2B3_oP40_33_4a_6a at zero temperature and pressure v000 | view | 510411 |
Creators: Junhao Li and Ellad Tadmor
Contributor: tadmor
Publication Year: 2019
DOI: https://doi.org/10.25950/5853fb8f
Computes the cubic elastic constants for some common crystal types (fcc, bcc, sc, diamond) by calculating the hessian of the energy density with respect to strain. An estimate of the error associated with the numerical differentiation performed is reported.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Elastic constants for bcc Fe at zero temperature v006 | view | 4584 | |
| Elastic constants for bcc O at zero temperature v006 | view | 5703 | |
| Elastic constants for diamond O at zero temperature v001 | view | 6784 | |
| Elastic constants for fcc Fe at zero temperature v006 | view | 13082 | |
| Elastic constants for fcc O at zero temperature v006 | view | 7193 | |
| Elastic constants for sc Fe at zero temperature v006 | view | 12810 | |
| Elastic constants for sc O at zero temperature v006 | view | 11895 |
Creators:
Contributor: ilia
Publication Year: 2024
DOI: https://doi.org/10.25950/2f2c4ad3
Computes the equilibrium crystal structure and energy for an arbitrary crystal at zero temperature and applied stress by performing symmetry-constrained relaxation. The crystal structure is specified using the AFLOW prototype designation. Multiple sets of free parameters corresponding to the crystal prototype may be specified as initial guesses for structure optimization. No guarantee is made regarding the stability of computed equilibria, nor that any are the ground state.
Creators:
Contributor: ilia
Publication Year: 2025
DOI: https://doi.org/10.25950/866c7cfa
Computes the equilibrium crystal structure and energy for an arbitrary crystal at zero temperature and applied stress by performing symmetry-constrained relaxation. The crystal structure is specified using the AFLOW prototype designation. Multiple sets of free parameters corresponding to the crystal prototype may be specified as initial guesses for structure optimization. No guarantee is made regarding the stability of computed equilibria, nor that any are the ground state.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Equilibrium crystal structure and energy for FeO in AFLOW crystal prototype A2B3_cI80_206_ad_e v003 | view | 957000 | |
| Equilibrium crystal structure and energy for Fe in AFLOW crystal prototype A_cF4_225_a v003 | view | 445006 | |
| Equilibrium crystal structure and energy for Fe in AFLOW crystal prototype A_cI2_229_a v003 | view | 141571 | |
| Equilibrium crystal structure and energy for Fe in AFLOW crystal prototype A_hP2_194_c v003 | view | 174393 | |
| Equilibrium crystal structure and energy for Fe in AFLOW crystal prototype A_tP28_136_f2ij v003 | view | 589957 |
Creators:
Contributor: brunnels
Publication Year: 2022
DOI: https://doi.org/10.25950/2c59c9d6
Computes grain boundary energy for a range of tilt angles given a crystal structure, tilt axis, and material.
Creators: Daniel S. Karls and Junhao Li
Contributor: karls
Publication Year: 2019
DOI: https://doi.org/10.25950/2765e3bf
Equilibrium lattice constant and cohesive energy of a cubic lattice at zero temperature and pressure.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Equilibrium zero-temperature lattice constant for bcc Fe v007 | view | 8375 | |
| Equilibrium zero-temperature lattice constant for bcc O v007 | view | 6150 | |
| Equilibrium zero-temperature lattice constant for diamond Fe v007 | view | 5516 | |
| Equilibrium zero-temperature lattice constant for diamond O v007 | view | 4398 | |
| Equilibrium zero-temperature lattice constant for fcc Fe v007 | view | 8275 | |
| Equilibrium zero-temperature lattice constant for fcc O v007 | view | 6187 | |
| Equilibrium zero-temperature lattice constant for sc Fe v007 | view | 8205 | |
| Equilibrium zero-temperature lattice constant for sc O v007 | view | 4622 |
Creators: Daniel S. Karls and Junhao Li
Contributor: karls
Publication Year: 2019
DOI: https://doi.org/10.25950/c339ca32
Calculates lattice constant of hexagonal bulk structures at zero temperature and pressure by using simplex minimization to minimize the potential energy.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Equilibrium lattice constants for hcp Fe v005 | view | 29557 |
Creators:
Contributor: mjwen
Publication Year: 2024
DOI: https://doi.org/10.25950/9d9822ec
This Test Driver uses LAMMPS to compute the linear thermal expansion coefficient at a finite temperature under a given pressure for a cubic lattice (fcc, bcc, sc, diamond) of a single given species.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Linear thermal expansion coefficient of bcc Fe at 293.15 K under a pressure of 0 MPa v002 | view | 3499229 |
Creators: Matt Bierbaum
Contributor: mattbierbaum
Publication Year: 2019
DOI: https://doi.org/10.25950/6c43a4e6
Calculates the surface energy of several high symmetry surfaces and produces a broken-bond model fit. In latex form, the fit equations are given by:
E_{FCC} (\vec{n}) = p_1 (4 \left( |x+y| + |x-y| + |x+z| + |x-z| + |z+y| +|z-y|\right)) + p_2 (8 \left( |x| + |y| + |z|\right)) + p_3 (2 ( |x+ 2y + z| + |x+2y-z| + |x-2y + z| + |x-2y-z| + |2x+y+z| + |2x+y-z| +|2x-y+z| +|2x-y-z| +|x+y+2z| +|x+y-2z| +|x-y+2z| +|x-y-2z| ) + c
E_{BCC} (\vec{n}) = p_1 (6 \left( | x+y+z| + |x+y-z| + |-x+y-z| + |x-y+z| \right)) + p_2 (8 \left( |x| + |y| + |z|\right)) + p_3 (4 \left( |x+y| + |x-y| + |x+z| + |x-z| + |z+y| +|z-y|\right)) +c.
In Python, these two fits take the following form:
def BrokenBondFCC(params, index):
import numpy
x, y, z = index
x = x / numpy.sqrt(x**2.+y**2.+z**2.)
y = y / numpy.sqrt(x**2.+y**2.+z**2.)
z = z / numpy.sqrt(x**2.+y**2.+z**2.)
return params[0]*4* (abs(x+y) + abs(x-y) + abs(x+z) + abs(x-z) + abs(z+y) + abs(z-y)) + params[1]*8*(abs(x) + abs(y) + abs(z)) + params[2]*(abs(x+2*y+z) + abs(x+2*y-z) +abs(x-2*y+z) +abs(x-2*y-z) + abs(2*x+y+z) +abs(2*x+y-z) +abs(2*x-y+z) +abs(2*x-y-z) + abs(x+y+2*z) +abs(x+y-2*z) +abs(x-y+2*z) +abs(x-y-2*z))+params[3]
def BrokenBondBCC(params, x, y, z):
import numpy
x, y, z = index
x = x / numpy.sqrt(x**2.+y**2.+z**2.)
y = y / numpy.sqrt(x**2.+y**2.+z**2.)
z = z / numpy.sqrt(x**2.+y**2.+z**2.)
return params[0]*6*(abs(x+y+z) + abs(x-y-z) + abs(x-y+z) + abs(x+y-z)) + params[1]*8*(abs(x) + abs(y) + abs(z)) + params[2]*4* (abs(x+y) + abs(x-y) + abs(x+z) + abs(x-z) + abs(z+y) + abs(z-y)) + params[3]
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Broken-bond fit of high-symmetry surface energies in bcc Fe v004 | view | 104065 |
Creators:
Contributor: efuem
Publication Year: 2023
DOI: https://doi.org/10.25950/fca89cea
Computes the monovacancy formation energy and relaxation volume for cubic and hcp monoatomic crystals.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Monovacancy formation energy and relaxation volume for bcc Fe | view | 619664 |
Creators:
Contributor: efuem
Publication Year: 2023
DOI: https://doi.org/10.25950/c27ba3cd
Computes the monovacancy formation and migration energies for cubic and hcp monoatomic crystals.
| Test | Test Results | Link to Test Results page | Benchmark time
Usertime multiplied by the Whetstone Benchmark. This number can be used (approximately) to compare the performance of different models independently of the architecture on which the test was run.
Measured in Millions of Whetstone Instructions (MWI) |
|---|---|---|---|
| Vacancy formation and migration energy for bcc Fe | view | 3790057 |
| Test | Error Categories | Link to Error page |
|---|---|---|
| Elastic constants for FeO in AFLOW crystal prototype A2B3_cI80_206_ad_e at zero temperature and pressure v000 | other | view |
ElasticConstantsCubic__TD_011862047401_006
| Test | Error Categories | Link to Error page |
|---|---|---|
| Elastic constants for diamond Fe at zero temperature v001 | other | view |
ElasticConstantsHexagonal__TD_612503193866_004
| Test | Error Categories | Link to Error page |
|---|---|---|
| Elastic constants for hcp Fe at zero temperature v004 | other | view |
EquilibriumCrystalStructure__TD_457028483760_000
| Test | Error Categories | Link to Error page |
|---|---|---|
| Equilibrium crystal structure and energy for O in AFLOW crystal prototype A_mC16_12_2ij v000 | other | view |
EquilibriumCrystalStructure__TD_457028483760_002
EquilibriumCrystalStructure__TD_457028483760_003
| Test | Error Categories | Link to Error page |
|---|---|---|
| Equilibrium crystal structure and energy for Fe in AFLOW crystal prototype A_tP1_123_a v003 | other | view |
GrainBoundaryCubicCrystalSymmetricTiltRelaxedEnergyVsAngle__TD_410381120771_002
LatticeConstantHexagonalEnergy__TD_942334626465_005
| Test | Error Categories | Link to Error page |
|---|---|---|
| Equilibrium lattice constants for hcp O v005 | other | view |
LinearThermalExpansionCoeffCubic__TD_522633393614_001
| Test | Error Categories | Link to Error page |
|---|---|---|
| Linear thermal expansion coefficient of bcc Fe at 293.15 K under a pressure of 0 MPa v001 | other | view |
SurfaceEnergyCubicCrystalBrokenBondFit__TD_955413365818_004
| Test | Error Categories | Link to Error page |
|---|---|---|
| Broken-bond fit of high-symmetry surface energies in bcc Fe v004 | other | view |
VacancyFormationEnergyRelaxationVolume__TD_647413317626_001
| Test | Error Categories | Link to Error page |
|---|---|---|
| Monovacancy formation energy and relaxation volume for sc O | other | view |
VacancyFormationMigration__TD_554849987965_001
| Test | Error Categories | Link to Error page |
|---|---|---|
| Vacancy formation and migration energy for sc O | other | view |
No Driver
| Verification Check | Error Categories | Link to Error page |
|---|---|---|
| MemoryLeak__VC_561022993723_004 | other | view |
| PeriodicitySupport__VC_895061507745_004 | other | view |
| Tersoff_LAMMPS_ByggmastarNagelAlbe_2019_FeO__MO_608695023236_000.txz | Tar+XZ | Linux and OS X archive |
| Tersoff_LAMMPS_ByggmastarNagelAlbe_2019_FeO__MO_608695023236_000.zip | Zip | Windows archive |
This Model requires a Model Driver. Archives for the Model Driver Tersoff_LAMMPS__MD_077075034781_005 appear below.
| Tersoff_LAMMPS__MD_077075034781_005.txz | Tar+XZ | Linux and OS X archive |
| Tersoff_LAMMPS__MD_077075034781_005.zip | Zip | Windows archive |