Citations
This panel presents information regarding the papers that have cited the interatomic potential (IP) whose page you are on.
The OpenKIM machine learning based Deep Citation framework is used to determine whether the citing article actually used the IP in computations (denoted by "USED") or only provides it as a background citation (denoted by "NOT USED"). For more details on Deep Citation and how to work with this panel, click the documentation link at the top of the panel.
The word cloud to the right is generated from the abstracts of IP principle source(s) (given below in "How to Cite") and the citing articles that were determined to have used the IP in order to provide users with a quick sense of the types of physical phenomena to which this IP is applied.
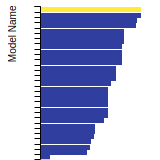
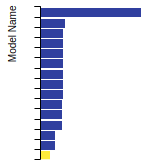
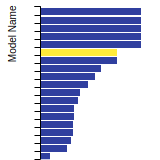
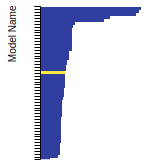
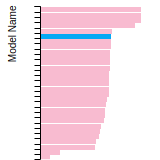
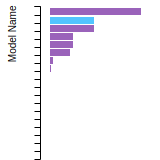
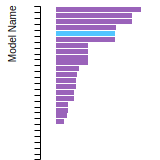
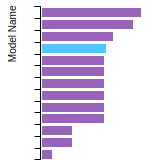
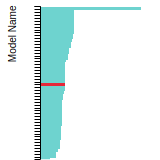
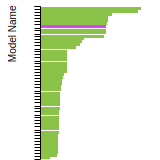
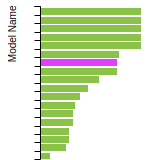
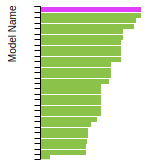
The bar chart shows the number of articles that cited the IP per year. Each bar is divided into green (articles that USED the IP) and blue (articles that did NOT USE the IP).
Users are encouraged to correct Deep Citation errors in determination by clicking the speech icon next to a citing article and providing updated information. This will be integrated into the next Deep Citation learning cycle, which occurs on a regular basis.
OpenKIM acknowledges the support of the Allen Institute for AI through the Semantic Scholar project for providing citation information and full text of articles when available, which are used to train the Deep Citation ML algorithm.
|
This panel provides information on past usage of this interatomic potential (IP) powered by the OpenKIM Deep Citation framework. The word cloud indicates typical applications of the potential. The bar chart shows citations per year of this IP (bars are divided into articles that used the IP (green) and those that did not (blue)). The complete list of articles that cited this IP is provided below along with the Deep Citation determination on usage. See the Deep Citation documentation for more information.
122 Citations (16 used)
Help us to determine which of the papers that cite this potential actually used it to perform calculations. If you know, click the .
USED (high confidence) J. Sun, P. Liu, M. Wang, and J. Liu, “Molecular Dynamics Simulations of Melting Iron Nanoparticles with/without Defects Using a Reaxff Reactive Force Field,” Scientific Reports. 2020. link Times cited: 21 USED (high confidence) J. Wang et al., “Impact of Nanoscale Roughness on Heat Transport across the Solid–Solid Interface,” Advanced Materials Interfaces. 2019. link Times cited: 30 Abstract: The performance of 1D nano/microbeam‐based devices greatly r… read moreAbstract: The performance of 1D nano/microbeam‐based devices greatly relies on heat dissipation to substrates. The surface roughness plays a key role in interfacial heat transport while this issue is seldom investigated due to the difficulty in quantitative determination of thermal contact resistance (TCR) at nanoscale. Here, the impact of interfacial roughness on heat transport at solid–solid interface by taking VO2 microbeam on Si substrate (VO2/Si) as a prototype is investigated. With the increased interface roughness from atomic fluctuation to ≈100 nm, it is found that an unusual uncertainty emerges in thermal interface transport along with the dramatical increase in TCR with two orders of magnitudes. Besides, a single‐layer graphene is inserted into VO2/Si interface as thermal interface material to study its performance under interface roughness. The inserted graphene not only substantially reduces the TCR but also reduces the uncertainty of thermal interface transport. This enhancement is even remarkable at rougher interface. Microscopic characterization and molecular dynamics simulation suggest that suspended condition and high heat conductivity of graphene on rough surface are responsible for the above effects. This work provides the quantitative evaluation of TCR and contributes to the in‐depth understanding on heat transport at imperfect interface. read less USED (high confidence) J. M. Sousa et al., “Elastic properties of graphyne-based nanotubes,” Computational Materials Science. 2019. link Times cited: 30 USED (high confidence) G. Barcaro, L. Sementa, V. Carravetta, T. Yano, M. Hara, and S. Monti, “Experimental and theoretical elucidation of catalytic pathways in TiO2-initiated prebiotic polymerization.,” Physical chemistry chemical physics : PCCP. 2019. link Times cited: 5 Abstract: The tendency of glycine to form polymer chains on a rutile(1… read moreAbstract: The tendency of glycine to form polymer chains on a rutile(110) surface under wet/dry conditions (dry-wet cycles at high temperature) is studied through a conjunction of surface sensitive experimental techniques and sequential periodic multilevel calculations that mimics the experimental procedures with models of decreasing complexity and increasing accuracy. X-ray photoemission spectroscopy (XPS) and thermal desorption spectroscopy (TDS) experimentally confirmed that the dry-wet cycles lead to Gly polymerization on the oxide support. This was supported by all the theoretical characterizations. First, classical reactive molecular dynamics (MD) simulations based on the ReaxFF approach were used to reproduce the adsorption of the experimental glycine solution droplets sprayed onto an oxide support and to identify the most probable arrangement of the molecules that triggered the polymerization mechanisms. Then, quantum chemistry density functional tight binding (DF-TB) MDs and static density functional theory (DFT) calculations were carried out to further explore favorable configurations and to evaluate the energy barriers of the most promising reaction pathways for the peptide bond-formation reactions. The results confirmed the fundamental role played by the substrate to thermodynamically and kinetically favor the process and disclosed its main function as an immobilizing agent: the molecules accommodated in the surface channels close to each other were the ones starting the key events of the dimerization process and the most favorable mechanism was the one where a water molecule acted as a proton exchange mediator in the condensation process. read less USED (low confidence) M. Darsin, B. Fachri, and H. Nurdiansyah, “Effect of particle size on ignition and oxidation of single aluminum: molecular dynamics study,” EUREKA: Physics and Engineering. 2023. link Times cited: 0 Abstract: Alumina nanoparticle is one of the attractive nanoparticles … read moreAbstract: Alumina nanoparticle is one of the attractive nanoparticles synthesized by the plasma method. The oxidation step in this method is challenging to explain experimentally. This work was to perform a molecular dynamics simulation to determine the oxidation mechanism of aluminum nanoparticles with different sizes and oxidation levels in the oxide layer. This work was to perform a molecular dynamics simulation to determine the oxidation mechanism of aluminum nanoparticles with different sizes and oxidation levels in the oxide layer. The simulation method employed the ReaxFF potential. The material used is aluminum nanoparticles in three different sizes (8, 12, and 16 nm) with an oxide layer thickness of 0.5 nm. Aluminum nanoparticles were given a relaxation treatment of 300 K for 1 ps and then heated to a temperature of 3250 K with a heating rate of 5×1013 K/s and cooled to 300 K. The ensemble used is a canonical ensemble with the Nose/Hoover thermostat method. The result shows that the higher the temperature applied to the system, the more oxygen molecules adsorption occurs on the surface of the oxide layer and the diffusion of oxygen to the particle core. The higher temperature applied also causes gaps, or void spaces, between the core and the shell. The reaction barrier for diffusion of oxygen also decreased significantly due to void space, and the surface of the aluminum core dissociates to the surface (alumina shell). Particles with a smaller size have a shorter ignition delay time. In addition, the smaller the particle size, the more oxygen molecules' reacted with aluminum particles in the particle core read less USED (low confidence) J. Hou et al., “Molecular Dynamics Simulation of Superheated Decomposition of Environmental Friendly C5F10O Mixture Gas,” 2022 4th International Conference on Smart Power & Internet Energy Systems (SPIES). 2022. link Times cited: 0 Abstract: SF 6 is widely used in electrical industry because… read moreAbstract: SF 6 is widely used in electrical industry because of its excellent insulation and arc extinguishing properties. However, the increasing use of SF 6 and its greenhouse effect cannot be ignored. In recent years, C5F 10O has attracted much attention as a substitute gas, but the theoretical study of its decomposition properties is still in the initial stage. In this study, ReaxFF reaction field was used to explore the decomposition mechanism of C 5F 10O under overheating condition from the perspective of molecular dynamics. The experimental results show that the free radicals produced by direct bond fracture of C5F 10O at high temperature mainly include CF 3-, C 4F 7O-, F- and C 5F 9O-, and these free radicals compound or convert into fluorocarbon compounds, such as CF 4 and C 2F 6. With the increase of temperature, the number and types of decomposition products of C 5F 10O increased. By analyzing the evolution trend of C 5F 10O molecular decomposition number, we speculated that C 5F 10O molecule has a certain self-reducing ability. Based on the toxicity of decomposition products, the comparison of practical application, and the comprehensive economic and practical engineering application, this paper suggests that air be used as buffer gas of C 5F 10O compared with N 2. read less USED (low confidence) M. Pols, T. Hilpert, I. Filot, A. V. van Duin, S. Calero, and S. Tao, “What Happens at Surfaces and Grain Boundaries of Halide Perovskites: Insights from Reactive Molecular Dynamics Simulations of CsPbI3,” ACS Applied Materials & Interfaces. 2022. link Times cited: 10 Abstract: The commercialization of perovskite solar cells is hindered … read moreAbstract: The commercialization of perovskite solar cells is hindered by the poor long-term stability of the metal halide perovskite (MHP) light-absorbing layer. Solution processing, the common fabrication method for MHPs, produces polycrystalline films with a wide variety of defects, such as point defects, surfaces, and grain boundaries. Although the optoelectronic effects of such defects have been widely studied, the evaluation of their impact on the long-term stability remains challenging. In particular, an understanding of the dynamics of degradation reactions at the atomistic scale is lacking. In this work, using reactive force field (ReaxFF) molecular dynamics simulations, we investigate the effects of defects, in the forms of surfaces, surface defects, and grain boundaries, on the stability of the inorganic halide perovskite CsPbI3. Our simulations establish a stability trend for a variety of surfaces, which correlates well with the occurrence of these surfaces in experiments. We find that a perovskite surface degrades by progressively changing the local geometry of PbIx octahedra from corner- to edge- to face-sharing. Importantly, we find that Pb dangling bonds and the lack of steric hindrance of I species are two crucial factors that induce degradation reactions. Finally, we show that the stability of these surfaces can be modulated by adjusting their atomistic details, by either creating additional point defects or merging them to form grain boundaries. While in general additional defects, particularly when clustered, have a negative impact on the material stability, some grain boundaries have a stabilizing effect, primarily because of the additional steric hindrance. read less USED (low confidence) I. Ponomarev, T. Polcar, and P. Nicolini, “Tribological properties of V2O5 studied via reactive molecular dynamics simulations,” Tribology International. 2021. link Times cited: 4 USED (low confidence) R.-K. Dong, Z. Mei, F. Zhao, S. Xu, and X. Ju, “Initial oxidation of nano-aluminum particles by H2O/H2O2: Molecular dynamics simulation,” International Journal of Hydrogen Energy. 2020. link Times cited: 8 USED (low confidence) J. Liu et al., “Combustion of Al nanoparticles coated with ethanol/ether molecules by non-equilibrium molecular dynamics simulations,” Materials today communications. 2020. link Times cited: 15 USED (low confidence) Q. Qiao, X. Li, and L. Huang, “Crystalline Cellulose under Pyrolysis Conditions: The Structure–Property Evolution via Reactive Molecular Dynamics Simulations,” Journal of Chemical & Engineering Data. 2020. link Times cited: 12 Abstract: As a primary component of cell walls of plants, algae, bacte… read moreAbstract: As a primary component of cell walls of plants, algae, bacteria, and other natural biomaterials, cellulose has attracted research attention and is the key to effective conversion of natural biomate... read less USED (low confidence) R.-K. Dong, Z. Mei, S. Xu, F. Zhao, X. Ju, and C. Ye, “Molecular dynamics simulation on reaction and kinetics isotope effect of nano-aluminum and water,” International Journal of Hydrogen Energy. 2019. link Times cited: 7 USED (low confidence) P. Liu, J. Liu, and M. Wang, “Ignition and combustion of nano-sized aluminum particles: A reactive molecular dynamics study,” Combustion and Flame. 2019. link Times cited: 53 USED (low confidence) A. Lazutin, A. A. Glagoleva, V. Vasilevskaya, and A. Khokhlov, “Computer synthesis of hypercrosslinked polystyrene: All-atom simulations,” Low Temperature Physics. 2017. link Times cited: 1 Abstract: For the first time a special force field ReaxFF is used to d… read moreAbstract: For the first time a special force field ReaxFF is used to describe the synthesis of polymer networks and for all-atom simulations of intermolecular cross linking in polystyrene. The density, specific surface, and coefficient of thermal expansion for sample networks with different degrees of crosslinking are calculated in the all-atom model. The results are in agreement with experimental data. read less USED (low confidence) Y. Zhong, X. Jing, S. Wang, and Q.-X. Jia, “Behavior investigation of phenolic hydroxyl groups during the pyrolysis of cured phenolic resin via molecular dynamics simulation,” Polymer Degradation and Stability. 2016. link Times cited: 48 USED (low confidence) B. Jeon, C. Ko, A. Duin, and S. Ramanathan, “Chemical stability and surface stoichiometry of vanadium oxide phases studied by reactive molecular dynamics simulations,” Surface Science. 2012. link Times cited: 15 NOT USED (low confidence) A. Ricchebuono, E. Vottero, A. Piovano, E. Groppo, P. Raybaud, and C. Chizallet, “Assessing Low-Cost Computational Methods against Structural Properties and Size Effects of Pt nanoparticles,” The Journal of Physical Chemistry C. 2023. link Times cited: 0 NOT USED (low confidence) U. Nwankwo, Y.-D. Wang, C. Lam, and N. Onofrio, “Charge equilibration model with shielded long-range Coulomb for reactive molecular dynamics simulations.,” The Journal of chemical physics. 2023. link Times cited: 1 Abstract: Atomic description of electrochemical systems requires react… read moreAbstract: Atomic description of electrochemical systems requires reactive interaction potential to explicitly describe the chemistry between atoms and molecules and the evolving charge distribution and polarization effects. Calculating Coulomb electrostatic interactions and polarization effects requires a better estimate of the partial charge distribution in molecular systems. However, models such as reactive force fields and charge equilibration (QEq) include Coulomb interactions up to a short-distance cutoff for better computational speeds. Ignoring long-distance electrostatic interaction affects the ability to describe electrochemistry in large systems. We studied the long-range Coulomb effects among charged particles and extended the QEq method to include long-range effects. By this extension, we anticipate a proper account of Coulomb interactions in reactive molecular dynamics simulations. We validate the approach by computing charges on a series of metal-organic frameworks and some simple systems. Results are compared to regular QEq and quantum mechanics calculations. The study shows slightly overestimated charge values in the regular QEq approach. Moreover, our method was combined with Ewald summation to compute forces and evaluate the long-range effects of simple capacitor configurations. There were noticeable differences between the calculated charges with/without long-range Coulomb interactions. The difference, which may have originated from the long-range influence on the capacitor ions, makes the Ewald method a better descriptor of Coulomb electrostatics for charged electrodes. The approach explored in this study enabled the atomic description of electrochemical systems with realistic electrolyte thickness while accounting for the electrostatic effects of charged electrodes throughout the dielectric layer in devices like batteries and emerging solid-state memory. read less NOT USED (low confidence) Q. Mao, M. Feng, X. Jiang, Y. Ren, K. Luo, and A. V. van Duin, “Classical and reactive molecular dynamics: Principles and applications in combustion and energy systems,” Progress in Energy and Combustion Science. 2023. link Times cited: 10 NOT USED (low confidence) Y. Ma et al., “Full-scale simulation and experimental verification of the phase-transition temperature of a VO2 nanofilm as smart window materials,” Materials Today Communications. 2023. link Times cited: 0 NOT USED (low confidence) T. Lu et al., “A Combined Experimental and Theoretical Study on Vanadium-Catalytic Oxidation of Lignin to Produce Carboxylic Acids,” SSRN Electronic Journal. 2022. link Times cited: 3 NOT USED (low confidence) A. Jacobson et al., “Effect of nanoconfinement and pore geometry on point of zero charge in synthesized mesoporous siliceous materials,” JCIS Open. 2022. link Times cited: 1 NOT USED (low confidence) G. Li et al., “Molecular Insight into Pyrolysis Processes via Reactive Force Field Molecular Dynamics: A State-of-the-art Review,” Journal of Analytical and Applied Pyrolysis. 2022. link Times cited: 12 NOT USED (low confidence) M. Dašić, I. Ponomarev, T. Polcar, and P. Nicolini, “Tribological properties of vanadium oxides investigated with reactive molecular dynamics,” Tribology International. 2022. link Times cited: 0 NOT USED (low confidence) I. Ponomarev, T. Polcar, and P. Nicolini, “New Reactive Force Field for Simulations of MoS2 Crystallization,” The Journal of Physical Chemistry. C, Nanomaterials and Interfaces. 2022. link Times cited: 7 Abstract: We present a new reactive force field (ReaxFF) parameter set… read moreAbstract: We present a new reactive force field (ReaxFF) parameter set for simulations of Mo–S structures. We compare our parameterization to the state-of-the-art ones in their performance against density functional theory (DFT) benchmarks and MoS2 crystallization simulations. Our new force field matches DFT data significantly better than any previously published force fields and provides a realistic layered MoS2 structure in crystallization simulations. It significantly improves the state-of-the-art force fields, which tend to crystallize in the experimentally unknown rock-salt MoS structure. Therefore, our new force field is a good candidate for further development and inclusion of other practically relevant elements, such as O, C, N, and H, which can be used to study the formation and tribological or catalytical properties of molybdenum disulfide. read less NOT USED (low confidence) W. Zhang, F. Starr, K. Beers, and J. Douglas, “Reactive Molecular Dynamics Simulations of the Depolymerization of Polyethylene Using Graphene-Oxide-Supported Platinum Nanoparticles.,” The journal of physical chemistry. A. 2022. link Times cited: 3 Abstract: While plastic materials offer many benefits to society, the … read moreAbstract: While plastic materials offer many benefits to society, the slow degradation and difficulty in recycling plastics raise important environmental and sustainability concerns. Traditional recycling efforts often lead to materials with inferior properties and correspondingly lower value, making them uneconomical to recycle. Recent efforts have shown promising chemical pathways for converting plastic materials into a wide range of value-added products, feedstocks or monomers. This is commonly referred to as "chemical recycling". Here, we use reactive molecular dynamics (MD) simulations to study the catalytic process of depolymerization of polyethylene (PE) using platinum (Pt) nanoparticles (NPs) in comparison to PE pyrolysis (thermal degradation). We apply a simple kinetic model to our MD results for the catalytic reaction rate as a function of temperature, from which we obtain the activation energy of the reaction, which shows the that the Pt NPs reduce the barrier for depolymerization. We further evaluate the molecular mass distribution of the reaction products to gain insight into the influence of the Pt NPs on reaction selectivity. Our results demonstrate the potential for the reactive MD method to help the design of recycling approaches for polymer materials. read less NOT USED (low confidence) Y. Han, Q. Gao, X. Guo, and T. Jiao, “Influence of external electric field on polymerization of Fe (III) flocculant in water: A reactive molecular dynamics and experiment study,” Journal of Molecular Liquids. 2022. link Times cited: 0 NOT USED (low confidence) R. Vaid, E. Yıldırım, M. Pasquinelli, and M. W. King, “Hydrolytic Degradation of Polylactic Acid Fibers as a Function of pH and Exposure Time,” Molecules. 2021. link Times cited: 18 Abstract: Polylactic acid (PLA) is a widely used bioresorbable polymer… read moreAbstract: Polylactic acid (PLA) is a widely used bioresorbable polymer in medical devices owing to its biocompatibility, bioresorbability, and biodegradability. It is also considered a sustainable solution for a wide variety of other applications, including packaging. Because of its widespread use, there have been many studies evaluating this polymer. However, gaps still exist in our understanding of the hydrolytic degradation in extreme pH environments and its impact on physical and mechanical properties, especially in fibrous materials. The goal of this work is to explore the hydrolytic degradation of PLA fibers as a function of a wide range of pH values and exposure times. To complement the experimental measurements, molecular-level details were obtained using both molecular dynamics (MD) simulations with ReaxFF and density functional theory (DFT) calculations. The hydrolytic degradation of PLA fibers from both experiments and simulations was observed to have a faster rate of degradation in alkaline conditions, with 40% of strength loss of the fibers in just 25 days together with an increase in the percent crystallinity of the degraded samples. Additionally, surface erosion was observed in these PLA fibers, especially in extreme alkaline environments, in contrast to bulk erosion observed in molded PLA grafts and other materials, which is attributed to the increased crystallinity induced during the fiber spinning process. These results indicate that spun PLA fibers function in a predictable manner as a bioresorbable medical device when totally degraded at end-of-life in more alkaline conditions. read less NOT USED (low confidence) C. She et al., “Reactive molecular dynamics simulation of thermal decomposition for nano-FOX-7,” Applied Physics A. 2021. link Times cited: 6 NOT USED (low confidence) C. Onwudinanti et al., “A ReaxFF Molecular Dynamics Study of Hydrogen Diffusion in Ruthenium–The Role of Grain Boundaries,” The Journal of Physical Chemistry. C, Nanomaterials and Interfaces. 2021. link Times cited: 3 Abstract: Ruthenium (Ru) thin films are used as protective caps for th… read moreAbstract: Ruthenium (Ru) thin films are used as protective caps for the multilayer mirrors in extreme ultraviolet lithography machines. When these mirrors are exposed to atomic hydrogen (H), it can permeate through Ru, leading to the formation of hydrogen-filled blisters on the mirrors. H has been shown to exhibit low solubility in bulk Ru, but the nature of H diffusion through Ru and its contribution to the mechanisms of blistering remain unknown. This work makes use of reactive molecular dynamics simulations to study the influence of imperfections in a Ru film on the behavior of H. For the Ru/H system, a ReaxFF force field which reproduces structures and energies obtained from quantum-mechanical calculations was parametrized. Molecular dynamics simulations have been performed with the newly developed force field to study the effect of tilt and twist grain boundaries on the overall diffusion behavior of H in Ru. Our simulations show that the tilt and twist grain boundaries provide energetically favorable sites for hydrogen atoms and act as sinks and highways for H. They therefore block H transport across their planes and favor diffusion along their planes. This results in the accumulation of hydrogen at the grain boundaries. The strong effect of the grain boundaries on hydrogen diffusion suggests tailoring the morphology of ruthenium thin films as a means to curb the rate of hydrogen permeation. read less NOT USED (low confidence) W. Liu et al., “Molecular Dynamics and Machine Learning in Catalysts,” Catalysts. 2021. link Times cited: 10 Abstract: Given the importance of catalysts in the chemical industry, … read moreAbstract: Given the importance of catalysts in the chemical industry, they have been extensively investigated by experimental and numerical methods. With the development of computational algorithms and computer hardware, large-scale simulations have enabled influential studies with more atomic details reflecting microscopic mechanisms. This review provides a comprehensive summary of recent developments in molecular dynamics, including ab initio molecular dynamics and reaction force-field molecular dynamics. Recent research on both approaches to catalyst calculations is reviewed, including growth, dehydrogenation, hydrogenation, oxidation reactions, bias, and recombination of carbon materials that can guide catalyst calculations. Machine learning has attracted increasing interest in recent years, and its combination with the field of catalysts has inspired promising development approaches. Its applications in machine learning potential, catalyst design, performance prediction, structure optimization, and classification have been summarized in detail. This review hopes to shed light and perspective on ML approaches in catalysts. read less NOT USED (low confidence) Y. Shin, Y. Gao, D. Shin, and A. Duin, “Impact of three-body interactions in a ReaxFF force field for Ni and Cr transition metals and their alloys on the prediction of thermal and mechanical properties,” Computational Materials Science. 2021. link Times cited: 8 NOT USED (low confidence) M. Pols, J. M. Vicent‐Luna, I. Filot, A. V. van Duin, and S. Tao, “Atomistic Insights Into the Degradation of Inorganic Halide Perovskite CsPbI3: A Reactive Force Field Molecular Dynamics Study,” The Journal of Physical Chemistry Letters. 2021. link Times cited: 25 Abstract: Halide perovskites make efficient solar cells but suffer fro… read moreAbstract: Halide perovskites make efficient solar cells but suffer from several stability issues. The characterization of these degradation processes is challenging because of the limited spatiotemporal resolution in experiments and the absence of efficient computational methods to study these reactive processes. Here, we present the first reactive force field for molecular dynamics simulations of the phase instability and the defect-induced degradation in CsPbI3. We find that the phase transitions are driven by the anharmonic fluctuations of the atoms in the perovskite lattice. At low temperatures, the Cs cations tend to move away from their preferential positions, resulting in worse contacts with the surrounding metal halide framework which initiates the conversion to a nonperovskite phase. Moreover, our simulations of defective structures reveal that, although both iodine vacancies and interstitials are mobile in the perovskite lattice, the vacancies have a detrimental effect on the stability, leading to the decomposition of perovskites to PbI2. read less NOT USED (low confidence) Y. Kim and J. Choi, “Oxide growth characteristics on Al (100), (110), and (111) surfaces: A chemo-mechanical evaluation,” Materials today communications. 2021. link Times cited: 9 NOT USED (low confidence) M. Duplančić, V. Gomzi, A. Pintar, S. Kurajica, and V. Tomašić, “Experimental and theoretical (ReaxFF) study of manganese-based catalysts for low-temperature toluene oxidation,” Ceramics International. 2020. link Times cited: 8 NOT USED (low confidence) F. Sun and W. Zeng, “Electric field effects on hydrogen/methane oxidation: A reactive force field based molecular dynamics study,” International Journal of Hydrogen Energy. 2020. link Times cited: 14 NOT USED (low confidence) T. D. Ta et al., “Reactive Molecular Dynamics Study of Hierarchical Tribochemical Lubricant Films at Elevated Temperatures.” 2020. link Times cited: 10 Abstract: We have developed a reactive force field (ReaxFF), which is … read moreAbstract: We have developed a reactive force field (ReaxFF), which is able to reproduce accurately the physical and chemical properties of a comprehensive Fe/Na/P/O system. This ReaxFF was trained systematic... read less NOT USED (low confidence) T. Si, K. Huang, Y. Lin, and M. Gu, “ReaxFF Study on the Effect of CaO on Cellulose Pyrolysis,” Energy & Fuels. 2019. link Times cited: 27 Abstract: The mechanism of cellulose pyrolysis with CaO is studied usi… read moreAbstract: The mechanism of cellulose pyrolysis with CaO is studied using a reactive force field in molecular dynamics simulations (ReaxFF MD). Through the analysis of the changes in the products and bonds ge... read less NOT USED (low confidence) G. Muñoz et al., “Redox activity of nickel and vanadium porphyrins: a possible mechanism behind petroleum genesis and maturation?,” RSC Advances. 2019. link Times cited: 13 Abstract: The presence of metalloporphyrins in crude oil has been know… read moreAbstract: The presence of metalloporphyrins in crude oil has been known for many years. In contrast, their role on the physical–chemical properties is only now beginning to be understood. In this study, we test using high-level ab initio calculations, the hypothesis of a possible redox catalytic activity of vanadium and nickel metalloporphyrins in crude oil, illustrated by the oxidation of methanol to formaldehyde and hydrogen dissociation, respectively. This process which may take place during petroleum genesis and maturation, explains some of its physical–chemical properties, such as polar chains, the absence of alcohols, the trapping of porphyrins within macromolecular aggregates. read less NOT USED (low confidence) Q. Qiao, C. Liu, W. Gao, and L. Huang, “Graphene oxide model with desirable structural and chemical properties,” Carbon. 2019. link Times cited: 22 NOT USED (low confidence) Y. Li, W. Fu, R. Tian, and C. Liang, “Mechanisms and stereoselectivities of phosphine-catalyzed (3+3) cycloaddition reaction between azomethine imine and ynone: A computational study,” International Journal of Quantum Chemistry. 2018. link Times cited: 1 NOT USED (low confidence) Y. K. Shin et al., “Development of a ReaxFF reactive force field for lithium ion conducting solid electrolyte Li1+xAlxTi2-x(PO4)3 (LATP).,” Physical chemistry chemical physics : PCCP. 2018. link Times cited: 17 Abstract: We developed a ReaxFF reactive force field for NASICON-type … read moreAbstract: We developed a ReaxFF reactive force field for NASICON-type Li1+xAlxTi2-x(PO4)3 (LATP) materials, which is a promising solid-electrolyte that may enable all-solid-state lithium-ion batteries. The force field parameters were optimized based on density functional theory (DFT) data, including equations of state and the heats of formation of ternary metal oxides and metal phosphate crystal phases (e.g., LixTiO2, Al2TiO5, LiAlO2, AlPO4, Li3PO4 and LiTi2(PO4)3 (LTP)), and the energy barriers for Li diffusion in TiO2 and LTP via vacancies and interstitial sites. Using ReaxFF, the structural and the energetic features of LATP were described properly across various compositions - Li occupies more preferentially the interstitial site next to Al than next to Ti. Also, as observed in experimental data, the lattice parameters decrease when Ti is partly substituted by Al because of the smaller size of the Al cation. Using this force field, the diffusion mechanism and the ionic conductivity of Li in LTP and LATP were investigated at T = 300-1100 K. Low ionic conductivity (5.9 × 10-5 S cm-1 at 300 K) was obtained in LTP as previously reported. In LATP at x = 0.2, the ionic conductivity was slightly improved (8.4 × 10-5 S cm-1), but it is still below the experimental value, which is on the order of 10-4 to 10-3 S cm-1 at x = 0.3-0.5. At higher x (higher Al composition), LATP has a configurational diversity due to the Al substitution and the concomitant insertion of Li. By performing a hybrid MC/MD simulation for LATP at x = 0.5, a thermodynamically stable LATP configuration was obtained. The ionic conductivity of this LATP configuration was calculated to be 7.4 × 10-4 S cm-1 at 300 K, which is one order of magnitude higher than the ionic conductivity for LTP and LATP at x = 0.2. This value is in good agreement with our experimental value (2.5 × 10-4 S cm-1 at 300 K) and the literature values. The composition-dependent ionic conductivity of LATP was successfully demonstrated using the ReaxFF reactive force field, verifying the applicability of the LATP force field for the understanding of Li diffusion and the design of highly Li ion conductive solid electrolytes. Furthermore, our results also demonstrate the feasibility of the MC/MD method in modeling LATP configuration, and provide compelling evidence for the solid solution sensitivity on ionic conductivity. read less NOT USED (low confidence) A. Rosales et al., “Application of Q2MM to predictions in stereoselective synthesis.,” Chemical communications. 2018. link Times cited: 19 Abstract: Quantum-Guided Molecular Mechanics (Q2MM) can be used to der… read moreAbstract: Quantum-Guided Molecular Mechanics (Q2MM) can be used to derive transition state force fields (TSFFs) that allow the fast and accurate predictions of stereoselectivity for a wide range of catalytic enantioselective reactions. The basic ideas behind the derivation of TSFFs using Q2MM are discussed and the steps involved in obtaining a TSFF using the Q2MM code, publically available at github.com/q2mm, are shown. The applicability for a range of reactions, including several non-standard applications of Q2MM, is demonstrated. Future developments of the method are also discussed. read less NOT USED (low confidence) S.-Y. Kim, H. W. Lee, S. J. Pai, and S. Han, “Activity, Selectivity, and Durability of Ruthenium Nanoparticle Catalysts for Ammonia Synthesis by Reactive Molecular Dynamics Simulation: The Size Effect.,” ACS applied materials & interfaces. 2018. link Times cited: 22 Abstract: We report a molecular dynamics (MD) simulation employing the… read moreAbstract: We report a molecular dynamics (MD) simulation employing the reactive force field (ReaxFF), developed from various first-principles calculations in this study, on ammonia (NH3) synthesis from nitrogen (N2) and hydrogen (H2) gases over Ru nanoparticle (NP) catalysts. Using ReaxFF-MD simulations, we predict not only the activities and selectivities but also the durabilities of the nanocatalysts and discuss the size effect and process conditions (temperature and pressure). Among the NPs (diameter = 3, 4, 5, and 10 nm) considered in this study, the 4 nm NPs show the highest activity, in contrast to our intuition that the smallest NP should provide the highest activity, as it has the highest surface area. In addition, the best selectivity is observed with the 10 nm NPs. The activity and selectivity are mainly determined by the hcp, fcc, and top sites on the Ru NP surface, which depend on the NP size. Moreover, the selectivity can be improved more significantly by increasing the H2 pressure than by increasing the N2 pressure. The durability of the NPs can be determined by the mean stress and the stress concentration, and these two factors have a trade-off relationship with the NP size. In other words, as the NP size increases, its mean stress decreases, whereas the stress concentration simultaneously increases. Because of these two effects, the best durability is found with the 5 nm NPs, which is also in contrast to our intuition that larger NPs should show better durability. We expect that ReaxFF-MD simulations, along with first-principles calculations, could be a useful tool in developing novel catalysts and understanding catalytic reactions. read less NOT USED (low confidence) C. Li, Z. Mei, F. Zhao, S. Xu, and X. Ju, “Molecular dynamic simulation for thermal decomposition of RDX with nano-AlH3 particles.,” Physical chemistry chemical physics : PCCP. 2018. link Times cited: 27 Abstract: Molecular dynamic simulation of a high explosive, RDX, mixed… read moreAbstract: Molecular dynamic simulation of a high explosive, RDX, mixed with AlH3 nanoparticles was performed by a newly parameterized ReaxFF force field. Testing of the ReaxFF shows that the mean absolute errors of the densities and bond lengths between calculated and experimental values are less than 7% and 3%, respectively. Using the ReaxFF, effects of AlH3 nanoparticles with different radii on the thermal decomposition of RDX were revealed. A new mechanism of the generation and the consumption of H2 was discovered in the explosion. The H2 is released by AlH3 firstly and then it reacts with NO2 and CO2 from the decomposition of RDX, leading to an increase of H2O, NO and CO. Meanwhile, the size effect of AlH3 upon the reaction was also revealed. As a result, the number of produced H2O and CO2 molecules increases by 10.38% and 56.85%, respectively, when the radius of AlH3 nanoparticles decreases from 1.10 to 0.68 nm. This showed that RDX decomposes more completely with smaller AlH3 nanoparticles, which was further demonstrated by the analysis of reaction residues and diffusion coefficients. read less NOT USED (low confidence) Y. Li, X. Zhang, S. Xiao, Q. Chen, and D. Wang, “Decomposition characteristics of C5F10O/air mixture as substitutes for SF6 to reduce global warming,” Journal of Fluorine Chemistry. 2018. link Times cited: 32 NOT USED (low confidence) S. Dinda, C. Chiu, A. Genest, and N. Rösch, “Evaluation of density functionals for elementary steps of selective oxidation reactions,” Computational and Theoretical Chemistry. 2017. link Times cited: 10 NOT USED (low confidence) Y. Shin, H. Kwak, A. Vasenkov, D. Sengupta, and A. Duin, “Development of a ReaxFF Reactive Force Field for Fe/Cr/O/S and Application to Oxidation of Butane over a Pyrite-Covered Cr2O3 Catalyst,” ACS Catalysis. 2015. link Times cited: 87 Abstract: We developed a ReaxFF force field for Fe/Cr/O/S, which is pa… read moreAbstract: We developed a ReaxFF force field for Fe/Cr/O/S, which is parametrized against data from quantum mechanical (QM) calculations. Using this force field, we studied the Cr-oxide catalyzed oxidation reaction of butane at 1600 K. Our simulation results demonstrate that the active oxygen species on the oxide surface play an important role in the conversion of butane. Dehydrogenation of butane, which is found to be catalyzed by oxygen species on the oxide surface, initiates the reaction and generates butane radicals and surface OH groups. The radical intermediates are associated with the oxygen atoms to form C–O bonds or make double bonds when neighboring carbon atoms are dehydrogenated, forming light alkenes. On the clean Cr-oxide, the major oxidation product is CH2O. The presence of iron pyrite (FeS2), a common inorganic component in coal-derived fuels and a major slagging component, on Cr-oxide accelerates the complete oxidation of butane forming CO2 and CO. Surface reconstruction by iron pyrite is probably r... read less NOT USED (low confidence) S. Naserifar, W. Goddard, T. Tsotsis, and M. Sahimi, “First principles-based multiparadigm, multiscale strategy for simulating complex materials processes with applications to amorphous SiC films.,” The Journal of chemical physics. 2015. link Times cited: 9 Abstract: Progress has recently been made in developing reactive force… read moreAbstract: Progress has recently been made in developing reactive force fields to describe chemical reactions in systems too large for quantum mechanical (QM) methods. In particular, ReaxFF, a force field with parameters that are obtained solely from fitting QM reaction data, has been used to predict structures and properties of many materials. Important applications require, however, determination of the final structures produced by such complex processes as chemical vapor deposition, atomic layer deposition, and formation of ceramic films by pyrolysis of polymers. This requires the force field to properly describe the formation of other products of the process, in addition to yielding the final structure of the material. We describe a strategy for accomplishing this and present an example of its use for forming amorphous SiC films that have a wide variety of applications. Extensive reactive molecular dynamics (MD) simulations have been carried out to simulate the pyrolysis of hydridopolycarbosilane. The reaction products all agree with the experimental data. After removing the reaction products, the system is cooled down to room temperature at which it produces amorphous SiC film, for which the computed radial distribution function, x-ray diffraction pattern, and the equation of state describing the three main SiC polytypes agree with the data and with the QM calculations. Extensive MD simulations have also been carried out to compute other structural properties, as well the effective diffusivities of light gases in the amorphous SiC film. read less NOT USED (low confidence) L. Zhao, C. Chiu, A. Genest, and N. Rösch, “DFT cluster model study of MoVO-type mixed-metal oxides,” Computational and Theoretical Chemistry. 2014. link Times cited: 7 NOT USED (low confidence) R. Addou, T. Senftle, N. O’Connor, M. Janik, A. V. van Duin, and M. Batzill, “Influence of hydroxyls on Pd atom mobility and clustering on rutile TiO(2)(011)-2 × 1.,” ACS nano. 2014. link Times cited: 49 Abstract: Understanding agglomeration of late transition metal atoms, … read moreAbstract: Understanding agglomeration of late transition metal atoms, such as Pd, on metal oxide supports, such as TiO2, is critical for designing heterogeneous catalysts as well as for controlling metal/oxide interfaces in general. One approach for reducing particle sintering is to modify the metal oxide surface with hydroxyls that decrease adatom mobility. We study by scanning tunneling microscopy experiments, density functional theory (DFT) calculations, and Monte Carlo (MC) computer simulations the atomistic processes of Pd sintering on a hydroxyl-modified TiO2(011)-2 × 1 surface. The formation of small 1-3 atom clusters that are stable at room temperature is achieved on the hydroxylated surface, while much larger clusters are formed under the same conditions on a hydroxyl-free surface. DFT shows that this is a consequence of stronger binding of Pd atoms adjacent to hydroxyls and increased surface diffusion barriers for Pd atoms on the hydroxylated surface. DFT, kinetic MC, and ReaxFF-based NVT-MC simulations show that Pd clusters larger than single Pd monomers can adsorb the hydrogen from the oxide surface and form Pd hydrides. This depletes the surface hydroxyl coverage, thus allowing Pd to more freely diffuse and agglomerate at room temperature. Experimentally, this causes a bimodal cluster size distribution with 1-3 atom clusters prevalent at low Pd coverage, while significantly larger clusters become dominant at higher Pd concentrations. This study demonstrates that hydroxylated oxide surfaces can significantly reduce Pd cluster sizes, thus enabling the preparation of surfaces populated with metal clusters composed of single to few atoms. read less NOT USED (low confidence) D. Wen and P. Song, “Numerical Simulation of Individual Metallic Nanoparticles.” 2014. link Times cited: 0 Abstract: Reactive metallic particles involve many complicated physica… read moreAbstract: Reactive metallic particles involve many complicated physical and chemical processes. Using molecular dynamics (MD) simulation as an example, this chapter explores the fundamental heating and reaction at the individual nanoparticle level. A brief overview of MD simulation is first introduced, and then the chapter focuses on the simulation of individual nanoparticle behavior related to ignition and combustion of energetic particles, which includes (i) size-dependent properties of individual nanoparticles, (ii) sintering and agglomeration of metallic nanoparticles, (iii) oxidation of nanoparticle in the presence of oxygen, and (iv) heating and cooling of core–shell-structured nanoparticles. This chapter provides some fundamental understanding the mechanism of reactive particles at the nanoscale, being complementary to bulk scale experiments and simulation. read less NOT USED (low confidence) M. Zheng et al., “Pyrolysis of Liulin Coal Simulated by GPU-Based ReaxFF MD with Cheminformatics Analysis,” Energy & Fuels. 2014. link Times cited: 172 Abstract: In this study, the first GPU-enabled ReaxFF MD program with … read moreAbstract: In this study, the first GPU-enabled ReaxFF MD program with significantly improved performance, surpassing CPU implementations, was employed to explore the initial chemical mechanisms and product distributions in pyrolysis of Liulin coal, a bituminous coal from Shanxi, PRC. The largest coal model ever used in simulation via ReaxFF MD, the Liulin coal molecular model consisting of 28 351 atoms was constructed based on a combination of experiments and classical coal models. The ReaxFF MD simulations at temperatures of 1000-2600 K were performed for 250 Ps to investigate the temperature effects on the product profile and the initial chemical reactions of the Liulin coal model pyrolysis. The generation rates of C-14-C-40 compounds and gas tend to equilibrate within 150-250 ps, indicating that the simulation should allow most of the thermal decomposition reactions complete and the simulated product profiles are reasonable for understanding the chemical reactions of the Liulin coal pyrolysis. The product (gas, tar, and char) evolution tendencies with time and temperature observed in the simulations are fairly in agreement with the experimental tendency reported in the literature. In particular, the evolution trends of three representative products (naphthalene, methyl-naphthalene and dimethyl-naphthalene) with temperature are very consistent with Py-GC/MS experiments. The detailed chemical reactions of the pyrolysis simulation have been generated using VARMD (Visualization and Analysis of Reactive Molecular Dynamics), which was newly created to examine the complexity of the chemical reaction network in ReaxFF MD simulation. The generation and consumption of HO center dot and H3C. radicals with time and temperature are reasonable and consistent both with the evolution of H2O and CH4, and with the detailed chemical reactions obtained as well. The amount of six-membered ring structures was observed to decrease with time and temperature, because of their conversion into 5-membered rings or 7-9-membered rings or even-larger-membered ring structures that will further open and decompose into small fragments. This work demonstrates a new methodology for investigating coal pyrolysis mechanism by combining GPU-enabled high-performance computing with cheminformatics analysis in ReaxFF MD. read less NOT USED (low confidence) I. Jacobs et al., “Conformational studies of ligand-template assemblies and the consequences for encapsulation of rhodium complexes and hydroformylation catalysis,” Catalysis Science & Technology. 2013. link Times cited: 12 Abstract: The second coordination sphere around a transition metal cat… read moreAbstract: The second coordination sphere around a transition metal catalyst can contribute to the activity and selectivity that it displays. In this paper we present encapsulated catalysts using a template-ligand assembly strategy based on Zn(II)salphen building blocks, and show that these have significantly different properties in catalysis than previously reported Zn(II)porphyrin-based analogues. The conformational properties of tris-Zn(II)salphen-based capsular catalysts were examined by a combination of solid state and solution phase analytical methods, as well as computational techniques. We found that as a result of the ability of the salphen-based capsules to adopt different conformations compared to porphyrin-based capsules, less stringent constraints are enforced to the catalytic centre, resulting in different catalyst selectivities displayed by the rhodium complexes enclosed. read less NOT USED (low confidence) T. Liang et al., “Reactive Potentials for Advanced Atomistic Simulations,” Materials Research-ibero-american Journal of Materials. 2013. link Times cited: 180 Abstract: This article reviews recent advances in the development of r… read moreAbstract: This article reviews recent advances in the development of reactive empirical force fields or potentials. In particular, we compare two widely used reactive potentials with variable-charge schemes that are desirable for multicomponent or multifunctional systems: the ReaxFF (reactive force field) and charge-optimized many-body (COMB) potentials. Several applications of these approaches in atomistic simulations that involve metal-based heterogeneous systems are also discussed. read less NOT USED (low confidence) D. A. Newsome, D. Sengupta, and A. Duin, “High-Temperature Oxidation of SiC-Based Composite: Rate Constant Calculation from ReaxFF MD Simulations, Part II,” Journal of Physical Chemistry C. 2013. link Times cited: 25 Abstract: Space vehicles often encounter very high temperature and har… read moreAbstract: Space vehicles often encounter very high temperature and harsh oxidative environments. To ensure proper thermal protection, layers composed of SiC and EPDM polymer are placed on the outer surface of the space vehicle. The O2 and H2O molecules are able to oxidize the SiC network, creating SiO2-type structures that may form a protective layer, while also pyrolyzing and burning the EPDM polymer, causing ablation. Reactive molecular dynamics simulations nicely complement experiment, as they provide direct observation and information to calculate physical parameters such as transport diffusivities and reaction constants. In this study, rate models were developed and molecular dynamics simulated trajectories were used to extract Arrhenius parameters that describe the initial stages of transport and kinetics of SiC oxidation by O2 and H2O and the combustion and pyrolysis of EPDM. The simulations showed that O2 was able to oxidize SiC more efficiently than H2O, with the transport activation barrier of O2 in the r... read less NOT USED (low confidence) A. Motta, M. Gaigeot, and D. Costa, “AIMD Evidence of Inner Sphere Adsorption of Glycine on a Stepped (101) Boehmite AlOOH Surface,” Journal of Physical Chemistry C. 2012. link Times cited: 20 Abstract: Adsorption of glycine, the smallest and simplest amino acid,… read moreAbstract: Adsorption of glycine, the smallest and simplest amino acid, on the (101) boehmite AlOOH stepped surface has been investigated at the solid/liquid water interface by means of ab initio molecular dynamics simulations at room temperature. The inner-sphere adsorption is shown to be the most favorable in energy, with either a glycinate located at the terrace or a zwitterion located at the step. Such conformations are dissected in terms of covalent and hydrogen bonds formed between the adduct and the surface and between the adduct and the surrounding water solvent at the interface. The outer-sphere adsorption of a zwitterionic glycine at the boehmite interface is found far less favorable in energy, where the compromise in the hydrogen bonds formed by glycine toward the surface and toward the solvent is detailed. Such outer-sphere adsorption is slightly more favorable than the solvation of the glycine molecule within the bulk liquid water. Glycine adsorption is also found to passivate the surface, as it hinders... read less NOT USED (low confidence) B. D. Jensen, A. Bandyopadhyay, K. Wise, and G. Odegard, “Parametric Study of ReaxFF Simulation Parameters for Molecular Dynamics Modeling of Reactive Carbon Gases.,” Journal of chemical theory and computation. 2012. link Times cited: 35 Abstract: The development of innovative carbon-based materials can be … read moreAbstract: The development of innovative carbon-based materials can be greatly facilitated by molecular modeling techniques. Although the Reax Force Field (ReaxFF) can be used to simulate the chemical behavior of carbon-based systems, the simulation settings required for accurate predictions have not been fully explored. Using the ReaxFF, molecular dynamics (MD) simulations are used to simulate the chemical behavior of pure carbon and hydrocarbon reactive gases that are involved in the formation of carbon structures such as graphite, buckyballs, amorphous carbon, and carbon nanotubes. It is determined that the maximum simulation time step that can be used in MD simulations with the ReaxFF is dependent on the simulated temperature and selected parameter set, as are the predicted reaction rates. It is also determined that different carbon-based reactive gases react at different rates, and that the predicted equilibrium structures are generally the same for the different ReaxFF parameter sets, except in the case of the predicted formation of large graphitic structures with the Chenoweth parameter set under specific conditions. read less NOT USED (low confidence) D. A. Newsome, D. Sengupta, H. Foroutan, M. F. Russo, and A. Duin, “Oxidation of Silicon Carbide by O2 and H2O: A ReaxFF Reactive Molecular Dynamics Study, Part I,” Journal of Physical Chemistry C. 2012. link Times cited: 158 Abstract: Simulations of the initial oxidation process of a SiC surfac… read moreAbstract: Simulations of the initial oxidation process of a SiC surface exposed to O2 and H2O molecules was studied with ReaxFF, an atomically detailed reactive molecular dynamics method that naturally models the breaking and forming of bonds. In this work, the ReaxFF forcefield was first expanded by training it with new quantum mechanics data of the binding energy, equation of state, and heat of formation of the SiC crystal, along with data from earlier studies that describes Si – Si, Si – O, and Si – H interactions. This expanded ReaxFF forcefield is capable of simultaneously describing both Si–C–O and Si–O–H bonding interactions. Using the forcefield, oxidation simulations were performed at various temperatures (in the range of 500 to 5000 K), and the trajectories were analyzed. The analyses showed that SiC gradually transforms into the oxides of silicon with simultaneous formation of a graphite-like layer. In presence of excess O2, the graphite-like layer was further oxidized to CO and CO2. We also analyzed the... read less NOT USED (low confidence) K. Farah, F. Müller-Plathe, and M. Böhm, “Classical reactive molecular dynamics implementations: state of the art.,” Chemphyschem : a European journal of chemical physics and physical chemistry. 2012. link Times cited: 71 Abstract: Reactive molecular dynamics (RMD) implementations equipped w… read moreAbstract: Reactive molecular dynamics (RMD) implementations equipped with force field approaches to simulate both the time evolution as well as chemical reactions of a broad class of materials are reviewed herein. We subdivide the RMD approaches developed during the last decade as well as older ones already reviewed in 1995 by Srivastava and Garrison and in 2000 by Brenner into two classes. The methods in the first RMD class rely on the use of a reaction cutoff distance and employ a sudden transition from the educts to the products. Due to their simplicity these methods are well suited to generate equilibrated atomistic or material-specific coarse-grained polymer structures. In connection with generic models they offer useful qualitative insight into polymerization reactions. The methods in the second RMD class are based on empirical reactive force fields and implement a smooth and continuous transition from the educts to the products. In this RMD class, the reactive potentials are based on many-body or bond-order force fields as well as on empirical standard force fields, such as CHARMM, AMBER or MM3 that are modified to become reactive. The aim with the more sophisticated implementations of the second RMD class is the investigation of the reaction kinetics and mechanisms as well as the evaluation of transition state geometries. Pure or hybrid ab initio, density functional, semi-empirical, molecular mechanics, and Monte Carlo methods for which no time evolution of the chemical systems is achieved are excluded from the present review. So are molecular dynamics techniques coupled with quantum chemical methods for the treatment of the reactive regions, such as Car-Parinello molecular dynamics. read less NOT USED (low confidence) D. Bedrov, G. D. Smith, and A. V. van Duin, “Reactions of singly-reduced ethylene carbonate in lithium battery electrolytes: a molecular dynamics simulation study using the ReaxFF.,” The journal of physical chemistry. A. 2012. link Times cited: 130 Abstract: We have conducted quantum chemistry calculations and gas- an… read moreAbstract: We have conducted quantum chemistry calculations and gas- and solution-phase reactive molecular dynamics simulation studies of reactions involving the ethylene carbonate (EC) radical anion EC(-) using the reactive force field ReaxFF. Our studies reveal that the substantial barrier for transition from the closed (cyclic) form, denoted c-EC(-), of the radical anion to the linear (open) form, denoted o-EC(-), results in a relatively long lifetime of the c-EC(-) allowing this compound to react with other singly reduced alkyl carbonates. Using ReaxFF, we systematically investigate the fate of both c-EC(-) and o-EC(-) in the gas phase and EC solution. In the gas phase and EC solutions with a relatively low concentration of Li(+)/x-EC(-) (where x = o or c), radical termination reactions between radical pairs to form either dilithium butylene dicarbonate (CH(2)CH(2)OCO(2)Li)(2) (by reacting two Li(+)/o-EC(-)) or ester-carbonate compound (by reacting Li(+)/o-EC(-) with Li(+)/c-EC(-)) are observed. At higher concentrations of Li(+)/x-EC(-) in solution, we observe the formation of diradicals which subsequently lead to formation of longer alkyl carbonates oligomers through reaction with other radicals or, in some cases, formation of (CH(2)OCO(2)Li)(2) through elimination of C(2)H(4). We conclude that the local ionic concentration is important in determining the fate of x-EC(-) and that the reaction of c-EC(-) with o-EC(-) may compete with the formation of various alkyl carbonates from o-EC(-)/o-EC(-) reactions. read less NOT USED (low confidence) E. G. Goken, K. L. Joshi, M. F. Russo, A. V. van Duin, and A. Castleman, “Effect of formic acid addition on water cluster stability and structure.,” The journal of physical chemistry. A. 2011. link Times cited: 10 Abstract: Computational chemistry simulations were performed to determ… read moreAbstract: Computational chemistry simulations were performed to determine the effect that the addition of a single formic acid molecule has on the structure and stability of protonated water clusters. Previous experimental studies showed that addition of formic acid to protonated pure water results in higher intensities of large-sized clusters when compared to pure water and methanol-water mixed clusters. For larger, protonated clusters, molecular dynamics simulations were performed on H(+)(H(2)O)(n), H(+)(H(2)O)(n)CH(3)OH, and H(+)(H(2)O)(n)CHOOH clusters, 19-28 molecules in size, using a reactive force field (ReaxFF). Based on these computations, formic acid-water clusters were found to have significantly higher binding energies per molecule. Addition of formic acid to a water cluster was found to alter the structure of the hydrogen-bonding network, creating selective sites within the cluster, enabling the formation of new hydrogen bonds, and increasing both the stability of the cluster and its rate of growth. read less NOT USED (low confidence) J. Mathews, A. Duin, and A. Chaffee, “The utility of coal molecular models,” Fuel Processing Technology. 2011. link Times cited: 166 NOT USED (low confidence) W. Goddard, J. Mueller, K. Chenoweth, and A. Duin, “ReaxFF Monte Carlo reactive dynamics. Application to resolving the partial occupations of the M1 phase of the MoVNbTeO catalyst,” Catalysis Today. 2010. link Times cited: 27 NOT USED (low confidence) C. R. Corbeil, C. R. Corbeil, and N. Moitessier, “Theory and application of medium to high throughput prediction method techniques for asymmetric catalyst design,” Journal of Molecular Catalysis A-chemical. 2010. link Times cited: 21 NOT USED (low confidence) O. Rahaman et al., “Development of a ReaxFF reactive force field for aqueous chloride and copper chloride.,” The journal of physical chemistry. A. 2010. link Times cited: 52 Abstract: Copper ions play crucial roles in many enzymatic and aqueous… read moreAbstract: Copper ions play crucial roles in many enzymatic and aqueous processes. A critical analysis of the fundamental properties of copper complexes is essential to understand their impact on a wide range of chemical interactions. However the study of copper complexes is complicated by the presence of strong polarization and charge transfer effects, multiple oxidation states, and quantum effects like Jahn-Teller distortions. These complications make the experimental observations difficult to interpret. In order to provide a computationally inexpensive yet reliable method for simulation of aqueous-phase copper chemistry, ReaxFF reactive force field parameters have been developed. The force field parameters have been trained against a large set of DFT-derived energies for condensed-phase copper-chloride clusters as well as chloride/water and copper-chloride/water clusters sampled from molecular dynamics (MD) simulations. The parameters were optimized by iteratively training them against configurations generated from ReaxFF MD simulations that are performed multiple times with improved sets of parameters. This cycle was repeated until the ReaxFF results were in accordance with the DFT-derived values. We have performed MD simulations on chloride/water and copper-chloride/water systems to validate the optimized force field. The structural properties of the chloride/water system are in accord with previous experimental and computational studies. The properties of copper-chloride/water agreed with the experimental observations including evidence of the Jahn-Teller distortion. The results of this study demonstrate the applicability of ReaxFF for the precise characterization of aqueous copper chloride. This force field provides a base for the design of a computationally inexpensive tool for the investigation of various properties and functions of metal ions in industrial, environmental, and biological environments. read less NOT USED (low confidence) K. Chenoweth, A. V. van Duin, and W. Goddard, “The ReaxFF Monte Carlo reactive dynamics method for predicting atomistic structures of disordered ceramics: application to the Mo(3)VO(x) catalyst.,” Angewandte Chemie. 2009. link Times cited: 49 Abstract: The ReaxFF computational approach is used to resolve partial… read moreAbstract: The ReaxFF computational approach is used to resolve partial or mixed occupation of crystallographic sites of the Mo_3VO_x multimetal oxide (MMO) catalyst. It provides insight into the oxidation state and coordination environment of the metal sites, identifies donor-acceptor networks in the catalyst, and predicts selectivity for molecular diffusion into channels of the framework. read less NOT USED (low confidence) W. Zhu, R. Yetter, J. E. Boyer, and A. V. van Duin, “Mechanistic study of chemical looping reactions between solid carbon fuels and CuO,” Combustion and Flame. 2022. link Times cited: 3 NOT USED (low confidence) Y. Cheng, Y. Zhao, F. Zhao, S. Xu, X. Ju, and C. Ye, “ReaxFF simulations on the combustion of Al and n-butanol nanofluid,” Fuel. 2022. link Times cited: 8 NOT USED (low confidence) Y. Shin, C. M. Ashraf, and A. Duin, “Development and Applications of the ReaxFF Reactive Force Field for Biological Systems.” 2021. link Times cited: 2 NOT USED (low confidence) Y. Pu, C. Liu, Q. Li, X. Xu, and E. Huo, “Pyrolysis mechanism of HFO-1234yf with R32 by ReaxFF MD and DFT method,” International Journal of Refrigeration-revue Internationale Du Froid. 2020. link Times cited: 29 NOT USED (low confidence) H.-ran Li, D. Ren, and X. Cheng, “The theoretical investigation of the β-crystobalite structure under the effect of electric field,” Computational Materials Science. 2015. link Times cited: 4 NOT USED (low confidence) J. Mueller, “STRUCTURES, ENERGETICS AND REACTIONS OF HYDROCARBONS ON NICKEL.” 2010. link Times cited: 1 Abstract: To better understand and improve reactive processes on nicke… read moreAbstract: To better understand and improve reactive processes on nickel surfaces such as the catalytic steam reforming of hydrocarbons, the decomposition of hydrocarbons at fuel cell
anodes, and the growth of carbon nanotubes, we have performed atomistic studies of hydrocarbon adsorption and decomposition on low index nickel surfaces and nickel catalyst nanoparticles. Quantum mechanics (QM) calculations utilizing the PBE flavor of density functional theory (DFT) were performed on all CH_x and C_2H_y species to determine their structures and energies on Ni(111). In good agreement with experiments, we find that CH is the most stable form of CH_x on Ni(111). It is a stable intermediate in both methane dehydrogenation and CO methanation, while CH(2,ad) is only stable during methanation. We also find that nickel surface atoms play an important catalytic role in C-H bond formation and cleavage. For the C_2H_y species we find a low surface coverage decomposition pathway proceeding through CHCH_(ad), the most stable intermediate, and a high surface coverage pathway which proceeds through CCH_(3,ad), the next most stable intermediate. Our enthalpies along these pathways are consistent with experimental observations.
To extend our study to larger systems and longer time scales, we have developed the ReaxFF reactive force field to describe hydrocarbon decomposition and reformation on nickel catalyst surfaces. The ReaxFF parameters were fit to geometries and energy surfaces from DFT calculations involving a large number of reaction pathways and equations of state for nickel, nickel carbides, and various hydrocarbon species chemisorbed on Ni(111), Ni(110) and Ni(100). The resulting ReaxFF description was validated against additional DFT data to demonstrate its accuracy, and used to perform reaction dynamics (RD) simulations on methyl decomposition for comparison with experiment. Finally ReaxFF RD simulations were applied to the chemisorption and decomposition of six different hydrocarbons (methane, acetylene, ethylene, benzene, cyclohexane and propylene) on a 468 atom nickel nanoparticle. These simulations realistically model hydrocarbon feedstock decomposition and provide reaction pathways relevant to this part of the carbon nanotube growth process. They show that C-C π bonds provide a low barrier pathway for chemisorption, and that the low energy of subsurface C is an important driving force in breaking C-C bonds. read less NOT USED (low confidence) J. Gale and K. Wright, “Lattice Dynamics from Force-Fields as a Technique for Mineral Physics,” Reviews in Mineralogy & Geochemistry. 2010. link Times cited: 7 Abstract: Theory and computation play an increasingly important role i… read moreAbstract: Theory and computation play an increasingly important role in the field of mineral physics by allowing the scientist to probe environments, such as the deep Earth, that are challenging or impossible to access extensively by experiment. Quantum mechanical methods are often the technique of choice, usually based on Kohn-Sham density functional theory as the computationally most practical approach for solids. Although calculations at this level can already be performed on thousands of atoms (Soler et al. 2002; Cankurtaran et al. 2008), the ability to sample nuclear configuration space is often restricted. While density functional theory is typically considered the defacto standard, it is important to remember that with current functionals the results will typically be quantitatively in error with respect to experiment, with occasional qualitative errors (Bilic and Gale 2009). The strength of the method is that the errors are generally systematic and can be anticipated a priori .
Despite the ever-increasing scope of electronic structure theory for condensed phases, there are still many problems that will lie beyond their reach for the foreseeable future. Consequently, there remains a need for more approximate, but efficient, techniques to complement quantum mechanical studies. Semi-empirical Hamiltonians and tight binding represent one possibility, but if even greater speed is required then force-field methods are a valuable option. As will be discussed later, the boundaries between the aforementioned approaches are continually becoming blurred as the sophistication of force-fields increases. Beside the greater speed, force-field methods have the advantage of a clear conceptual connection between the functional form and the underlying physics. Hence much can be learnt about what physical interactions are important to describe the properties of a system.
The use of force-field methods is widespread from biological modelling to mineralogy, aided by the availability of many different programs for interatomic potential simulation. By … read less NOT USED (low confidence) S. Keten, J. Bertaud, D. Sen, Z. Xu, T. Ackbarow, and M. Buehler, “Multiscale Modeling of Biological Protein Materials – Deformation and Failure.” 2010. link Times cited: 1 NOT USED (high confidence) S. Eskandari, J. Koltai, I. László, M. Vaezi, and J. Kürti, “Formation of nanoribbons by carbon atoms confined in a single-walled carbon nanotube-A molecular dynamics study.,” The Journal of chemical physics. 2023. link Times cited: 0 Abstract: Carbon nanotubes can serve as one-dimensional nanoreactors f… read moreAbstract: Carbon nanotubes can serve as one-dimensional nanoreactors for the in-tube synthesis of various nanostructures. Experimental observations have shown that chains, inner tubes, or nanoribbons can grow by the thermal decomposition of organic/organometallic molecules encapsulated in carbon nanotubes. The result of the process depends on the temperature, the diameter of the nanotube, and the type and amount of material introduced inside the tube. Nanoribbons are particularly promising materials for nanoelectronics. Motivated by recent experimental results observing the formation of carbon nanoribbons inside carbon nanotubes, molecular dynamics calculations were performed with the open source LAMMPS code to investigate the reactions between carbon atoms confined within a single-walled carbon nanotube. Our results show that the interatomic potentials behave differently in quasi-one-dimensional simulations of nanotube-confined space than in three-dimensional simulations. In particular, the Tersoff potential performs better than the widely used Reactive Force Field potential in describing the formation of carbon nanoribbons inside nanotubes. We also found a temperature window where the nanoribbons were formed with the fewest defects, i.e., with the largest flatness and the most hexagons, which is in agreement with the experimental temperature range. read less NOT USED (high confidence) J. Hu, Z. Wilde, P. Peralta, C. Muhich, and J. Oswald, “Predicting Hugoniot equation of state in erythritol with ab initio and reactive molecular dynamics,” Journal of Applied Physics. 2021. link Times cited: 0 Abstract: Erythritol has been proposed as an inert surrogate for devel… read moreAbstract: Erythritol has been proposed as an inert surrogate for developing theoretical and computational models to study aging in energetic materials. In this work, we present a comparison of mechanical and shock properties of erythritol computed using the ReaxFF reactive force field and from ab initio calculations employing density functional theory (DFT). We screened eight different ReaxFF parameterizations, of which the CHO parameters developed for hydrocarbon oxidation provide the most accurate predictions of mechanical properties and the crystal structure of erythritol. Further validation of the applicability of this ReaxFF parameterization for modeling erythritol is demonstrated by comparing predictions of the elastic constants, crystal structure, vibrational density of states, and Hugoniot curves against DFT calculations. The ReaxFF predictions are in close agreement with the DFT simulations for the elastic constants and shock Hugoniot when the crystal is loaded along its c axis but show as much as 30% disagreement in the elastic constants in the a b plane and 12% difference in shock pressures when shocked along the a or b crystal axes. Last, we compare thermomechanical properties predicted from classical molecular dynamics with those calculated using the quasi-harmonic approximation and show that quantum mechanical effects produce large discrepancies in the computed values of heat capacity and thermal expansion coefficients compared with classical assumptions. Combining classical molecular dynamics predictions of mechanical behavior with phonon-based calculations of thermal behaviors, we show that predicted shock-induced temperatures for pressures up to 6.5 GPa do not exceed the pressure-dependent melting point of erythritol. read less NOT USED (high confidence) R. K. Shayakhmetova and E. Khamitov, “ReaxFF Molecular Dynamics Simulation of the Cracking of Components of Vacuum Gasoil in the Presence of a Nickel Nanocluster,” Russian Journal of Physical Chemistry A. 2021. link Times cited: 0 NOT USED (high confidence) X.-K. Wang, Y. Zhao, F. Zhao, S. Xu, and X. Ju, “Reactive molecular dynamics simulation of thermal decomposition for nitromethane/nano-aluminum composites,” Journal of Molecular Modeling. 2020. link Times cited: 2 NOT USED (high confidence) X. Huang et al., “Comparison study of carbon clusters formation during thermal decomposition of 1,3,5-triamino-2,4,6-trinitrobenzene and benzotrifuroxan: a ReaxFF based sequential molecular dynamics simulation.,” Physical chemistry chemical physics : PCCP. 2020. link Times cited: 4 Abstract: Carbon rich clusters are usually found after the detonation … read moreAbstract: Carbon rich clusters are usually found after the detonation of explosives, which greatly hinder their further decomposition into small molecules. A comparison study of thermal decomposition and clusters formation between 1,3,5-triamino-2,4,6-trinitrobenzene (TATB) and benzotrifuroxan (BTF) crystals was conducted to uncover the mechanisms behind their distinct differences in sensitivity and reaction violence, which has not been investigated in detail. The simulations of heating at 3500 K, then expansion and cooling were conducted through reactive molecular dynamics using the ReaxFF-lg force field. As a result, the initial low decay rate indicates that TATB is more stable than BTF under high temperatures, while once ignited it decays faster than BTF. Nevertheless, BTF decomposes more completely with a higher potential energy release, a greater amount of final products, and higher reaction frequencies, and shows higher reaction violence than TATB. More and heavier clusters occur in TATB crystals compared with those in BTF. Large clusters form during the heating process and then partly dissociate during expansion and cooling. A faster cooling rate facilitates larger clusters formation. Graphitic geometries as well as carbon rings and carbon chains are common in the stable clusters. Besides, further simulations show that a lower heating temperature facilitates larger clusters formation both in TATB and BTF. Our results are expected to deepen the insight into the mechanisms of carbon clusters formation and the different performances of TATB and BTF. read less NOT USED (high confidence) S. M. Handrigan, L. Morrissey, and S. Nakhla, “Investigating various many-body force fields for their ability to predict reduction in elastic modulus due to vacancies using molecular dynamics simulations,” Molecular Simulation. 2019. link Times cited: 6 Abstract: ABSTRACT Molecular dynamics simulations are more frequently … read moreAbstract: ABSTRACT Molecular dynamics simulations are more frequently being utilised to predict macroscale mechanical properties as a result of atomistic defects. However, the interatomic force field can significantly affect the resulting mechanical properties. While several studies exist which demonstrate the ability of various force fields to predict mechanical properties, the investigation into which is most accurate for the investigation of vacancies is limited. To obtain meaningful predictions of mechanical properties, a clear understanding of force field parameterisation is required. As such, the current study evaluates various many-body force fields to demonstrate the reduction in mechanical properties of iron and iron–chromium due to the presence of vacancies while undergoing room temperature atomistic uniaxial tension. Reduction was normalised in each case with the zero-vacancy elastic modulus, removing the need to predict an accurate nominal elastic modulus. Comparisons were made to experimental data and an empirical model from literature. It was demonstrated that accurate fitting to vacancy formation and migration energy allowed for accurate predictions. In addition, bond-order based force fields showed enhanced predictions regardless of fitting procedure. Overall, these findings highlight the need to understand capabilities and limitations of available force fields, as well as the need for enhanced parameterisation of force fields. read less NOT USED (high confidence) Z. Mei, C. Li, F. Zhao, S. Xu, and X. Ju, “Reactive molecular dynamics simulation of thermal decomposition for nano-AlH3/TNT and nano-AlH3/CL-20 composites,” Journal of Materials Science. 2019. link Times cited: 20 NOT USED (high confidence) R. V. van Santen, A. Sengar, and E. Steur, “The challenge of catalyst prediction.,” Faraday discussions. 2018. link Times cited: 8 Abstract: New insights and successful use of computational catalysis a… read moreAbstract: New insights and successful use of computational catalysis are highlighted. This is within the context of remaining issues that prevent theoretical catalysis to be fully predictive of catalyst performance. A major challenge is to include in modelling studies the transient initiation as well as deactivation processes of the catalyst. We will illustrate this using as an example for solid acid catalysis, the alkylation process, and for transition metal catalysis, the Fischer-Tropsch reaction. For the alkylation reaction of isobutane and alkene, an important reaction for high octane gasoline, we will present a deactivation model. For the Fischer-Tropsch reaction, which converts synthesis gas into gasoline grade molecules, we discuss structural reorganization of the catalyst induced by reaction. read less NOT USED (high confidence) Y. Chen, H. Xiao, Y. Liu, and X. Chen, “Effects of temperature and strain rate on mechanical behaviors of Stone-Wales defective monolayer black phosphorene,” Journal of Physical Chemistry C. 2017. link Times cited: 15 Abstract: The mechanical behaviors of monolayer black phosphorene (MBP… read moreAbstract: The mechanical behaviors of monolayer black phosphorene (MBP) are explored by molecular dynamics (MD) simulations using a reactive force field. It is revealed that the temperature and strain rate have a significant influence on the mechanical behavior of MBP, and they are further weakened by SW (Stone–Wales) defects. In general, the tensile strength for both the pristine and SW defective MBP decreases with the increase of temperature or decrease of strain rate. Surprisingly, for relatively high temperature (>300 K) and low strain rate (<5.0 × 10–8 fs–1), a phase transition from the black phosphorene to a mixture of β-phase (β-P) and γ-phase (γ-P) is observed for the SW-2 defective MBP under armchair tension, while self-healing of the SW-2 defect is observed under zigzag tension. A deformation map of SW-2 defective MBP under armchair tension at different temperature and strain rate is established, which is useful for the design of phosphorene allotropes by strain. The results presented herein yield useful ... read less NOT USED (high confidence) S. Reddivari, C. Lastoskie, R. Wu, and J. Zhang, “Chemical composition and formation mechanisms in the cathode-electrolyte interface layer of lithium manganese oxide batteries from reactive force field (ReaxFF) based molecular dynamics,” Frontiers in Energy. 2017. link Times cited: 8 NOT USED (high confidence) H. Chu, L. Cao, X. Peng, and G. Li, “Polarizable force field development for lipids and their efficient applications in membrane proteins,” Wiley Interdisciplinary Reviews: Computational Molecular Science. 2017. link Times cited: 9 Abstract: Polarizable force fields have been developed due to the intr… read moreAbstract: Polarizable force fields have been developed due to the intrinsic problem of additive force fields in modeling electrostatic interactions. Because of the capability to accurately describe the behavior of systems with significant changes in their electrostatic environments, polarizable force fields might be a decent tool to study membrane‐related systems, such as lipid bilayers, though not so much progresses have been made. In this overview article we described the developments of a variety of polarizable force fields, including the corresponding theories, benchmark examples, and more specifically we were focused on the applications on lipid membranes. WIREs Comput Mol Sci 2017, 7:e1312. doi: 10.1002/wcms.1312 read less NOT USED (high confidence) S. Reddivari, C. Lastoskie, R. Wu, and J. Zhang, “Chemical composition and formation mechanisms in the cathode-electrolyte interface layer of lithium manganese oxide batteries from reactive force field (ReaxFF) based molecular dynamics,” Frontiers in Energy. 2017. link Times cited: 0 NOT USED (high confidence) X. Zhang, Y. Wu, X. Chen, H. Wen, and S. Xiao, “Theoretical Study on Decomposition Mechanism of Insulating Epoxy Resin Cured by Anhydride,” Polymers. 2017. link Times cited: 33 Abstract: High temperatures caused by partial discharge results in the… read moreAbstract: High temperatures caused by partial discharge results in the decomposition of insulating epoxy resins in electrical equipment. In this paper, the ReaxFF force field is used to investigate the decomposition process of epoxy resins cured by anhydride and the formation mechanisms of small-molecule gases. Results show that the initiation reaction is the cleavage of an ester bond linked with an epoxy resin. Produced by the decomposition of ester groups, CO2 is the first and most abundant product. Meanwhile, CH2O can be generated through three main ways, although the process still depends on the decomposition of epoxy functional groups. H2O is produced by free radical collision and dehydration. The production of small-molecule gases has the following sequence: CO2, CH2O, CO, and H2O. The produced gases have the following order according to amount: CO2, CH2O, H2O, and CO. read less NOT USED (high confidence) E. Neyts and K. M. Bal, “Effect of electric fields on plasma catalytic hydrocarbon oxidation from atomistic simulations,” Plasma Processes and Polymers. 2017. link Times cited: 9 NOT USED (high confidence) P. Li and K. Merz, “Metal Ion Modeling Using Classical Mechanics,” Chemical Reviews. 2017. link Times cited: 230 Abstract: Metal ions play significant roles in numerous fields includi… read moreAbstract: Metal ions play significant roles in numerous fields including chemistry, geochemistry, biochemistry, and materials science. With computational tools increasingly becoming important in chemical research, methods have emerged to effectively face the challenge of modeling metal ions in the gas, aqueous, and solid phases. Herein, we review both quantum and classical modeling strategies for metal ion-containing systems that have been developed over the past few decades. This Review focuses on classical metal ion modeling based on unpolarized models (including the nonbonded, bonded, cationic dummy atom, and combined models), polarizable models (e.g., the fluctuating charge, Drude oscillator, and the induced dipole models), the angular overlap model, and valence bond-based models. Quantum mechanical studies of metal ion-containing systems at the semiempirical, ab initio, and density functional levels of theory are reviewed as well with a particular focus on how these methods inform classical modeling efforts. Finally, conclusions and future prospects and directions are offered that will further enhance the classical modeling of metal ion-containing systems. read less NOT USED (high confidence) Y. Shin, L. Gai, S. Raman, and A. V. van Duin, “Development of a ReaxFF Reactive Force Field for the Pt-Ni Alloy Catalyst.,” The journal of physical chemistry. A. 2016. link Times cited: 59 Abstract: We developed the ReaxFF force field for Pt/Ni/C/H/O interact… read moreAbstract: We developed the ReaxFF force field for Pt/Ni/C/H/O interactions, specifically targeted for heterogeneous catalysis application of the Pt-Ni alloy. The force field is trained using the DFT data for equations of state of Pt3Ni, PtNi3 and PtNi alloys, the surface energy of the PtxNi1-x(111) (x = 0.67-0.83), and binding energies of various atomic and molecular species (O, H, C, CH, CH2, CH3, CO, OH, and H2O) on these surfaces. The ReaxFF force field shows a Pt surface segregation at x ≥ 0.67 for the (111) surface and x ≥ 0.62 for the (100) surface in vacuum. In addition, from the investigation of the preferential alloy component of the adsorbates, it is expected that H and CH3 on the alloy surface to induce a segregation of Pt whereas the oxidation intermediates and products such as C, O, OH, H2O, CO, CH, and CH2 are found to induce Ni segregation. The relative order of binding strengths among adsorbates is a function of alloy composition and the force field is trained to describe the trend observed in DFT calculations, namely, H2 < H2O < CH3 ≈ O2 ≈ CO < OH < CH2 < C ≈ CH on Pt8Ni4, H2 < H2O < CO ≈ O2 < CH3 < OH < CH2 < CH < C on Pt9Ni3, and H2 < H2O < O2 < CO < CH3 < OH < CH2 < C ≈ CH on Pt10Ni2. Using this force field, we performed the grand-canonical Monte Carlo (GCMC) and molecular dynamics (MD) simulations for a Pt3Ni slab and a truncated cuboctahedral nanoparticle terminated by (111) and (100) faces, to examine the surface segregation trend under different gas environments. It is found that Pt segregates to the alloy surface when the surface is exposed to vacuum and/or H2 environment while Ni segregates under the O2 environment. These results suggest that the Pt/Ni alloy force field can be successfully used for the preparation of Pt-Ni nanobimetallic catalysts structure using GCMC and run MD simulations to investigate its role and the catalytic chemistry in catalytic oxidation, dehydrogenation and coupling reactions. The current Pt/Ni force field still is found to have difficulties in describing the observed segregation trend in Ni-rich alloy compositions (x < 0.6), suggesting the need for additional force field training and evaluation for its application to describe the characteristics and chemistry of Ni-rich alloys. read less NOT USED (high confidence) B. Koo, N. Subramanian, and A. Chattopadhyay, “Molecular dynamics study of brittle fracture in epoxy-based thermoset polymer,” Composites Part B-engineering. 2016. link Times cited: 52 NOT USED (high confidence) P. Shamberger, J. Wohlwend, A. Roy, and A. Voevodin, “Investigating Grain Boundary Structures and Energetics of Rutile with Reactive Molecular Dynamics,” Journal of Physical Chemistry C. 2016. link Times cited: 4 Abstract: Determining quantitative grain boundary (GB) energies as a f… read moreAbstract: Determining quantitative grain boundary (GB) energies as a function of microscopic orientation parameters is essential in order to understand the population of boundaries present in polycrystalline ceramics and films, and the physical properties that result from these boundaries. Here, we investigate the use of two reactive potentials, COMB3 and ReaxFF, to predict free surface and grain boundary structures and energies in the TiO2 rutile system, and compare these results against previously reported ab initio surface and interfacial energies. We demonstrate reactive MD potentials to be generally capable of reproducing key features anticipated for GB structures and energetics, including relative GB and surface energy, charge distributions and potential for different polar and nonpolar terminations, and energy cusps at low-energy interfaces (e.g., coherent twin boundaries, coherent site lattice boundaries). This work establishes the foundation for further use of reactive MD to simulate libraries of oxide GBs... read less NOT USED (high confidence) A. Pathak, S. Nedea, A. V. van Duin, H. Zondag, C. Rindt, and D. Smeulders, “Reactive force field development for magnesium chloride hydrates and its application for seasonal heat storage.,” Physical chemistry chemical physics : PCCP. 2016. link Times cited: 21 Abstract: MgCl2 hydrates are considered as high-potential candidates f… read moreAbstract: MgCl2 hydrates are considered as high-potential candidates for seasonal heat storage materials. These materials have high storage capacity and fast dehydration kinetics. However, as a side reaction to dehydration, hydrolysis may occur. Hydrolysis is an irreversible reaction, which produces HCl gas thus affecting the durability of heat storage systems. In this study, we present the parameterization of a reactive force field (ReaxFF) for MgCl2 hydrates to study the dehydration and hydrolysis kinetics of MgCl2·H2O and MgCl2·2H2O. The ReaxFF parameters have been derived by training against quantum mechanics data obtained from Density Functional Theory (DFT) calculations consisting of bond dissociation curves, angle bending curves, reaction enthalpies, and equation of state. A single-parameter search algorithm in combination with a Metropolis Monte Carlo algorithm is successfully used for this ReaxFF parameterization. The newly developed force field is validated by examining the elastic properties of MgCl2 hydrates and the proton transfer reaction barrier, which is important for the hydrolysis reaction. The bulk moduli of MgCl2·H2O and MgCl2·2H2O obtained from ReaxFF are in close agreement with the bulk moduli obtained from DFT. A barrier of 20.24 kcal mol(-1) for the proton transfer in MgCl2·2H2O is obtained, which is in good agreement with the barrier (19.55 kcal mol(-1)) obtained from DFT. Molecular dynamics simulations using the newly developed ReaxFF on 2D-periodic slabs of MgCl2·H2O and MgCl2·2H2O show that the dehydration rate increases more rapidly with temperature in MgCl2·H2O than in MgCl2·2H2O, in the temperature range 300-500 K. The onset temperature of HCl formation, a crucial design parameter in seasonal heat storage systems, is observed at 340 K for MgCl2·H2O, which is in agreement with experiments. The HCl formation is not observed for MgCl2·2H2O. The diffusion coefficient of H2O through MgCl2·H2O is lower than through MgCl2·2H2O, and can become a rate-limiting step. The diffusion coefficient increases with temperature and follows the Arrhenius law both for MgCl2·H2O and MgCl2·2H2O. These results indicate the validity of the ReaxFF approach for studying MgCl2 hydrates and provide important atomistic-scale insight of reaction kinetics and H2O transport in these materials. read less NOT USED (high confidence) Y. Han, D. D. Jiang, J. Zhang, W. Li, Z. Gan, and J. Gu, “Development, applications and challenges of ReaxFF reactive force field in molecular simulations,” Frontiers of Chemical Science and Engineering. 2016. link Times cited: 87 NOT USED (high confidence) F. Tielens et al., “Characterization of Phosphate Species on Hydrated Anatase TiO2 Surfaces.,” Langmuir : the ACS journal of surfaces and colloids. 2016. link Times cited: 19 Abstract: The adsorption/interaction of KH2PO4 with solvated (100) and… read moreAbstract: The adsorption/interaction of KH2PO4 with solvated (100) and (101) TiO2 anatase surfaces is investigated using periodic DFT calculations in combination with GIPAW NMR calculations and experimental IR and solid state (17)O, and (31)P NMR spectroscopies. A complete and realistic model has been used to simulate the solvent by individual water molecules. The most stable adsorption configurations are characterized theoretically at the atomic scale, and experimentally supported by NMR and IR spectroscopies. It is shown that H2PO4(-) chemisorbs on the (100) and (101) anatase surfaces, preferentially via a bidentate geometry. Dimer (H3P2O7(-)) and trimer (H4P3O10(-)) adsorption models are confronted with monomer adsorption models, in order to rationalize their occurrence. read less NOT USED (high confidence) C. Chiu, T. Vogt, L. Zhao, A. Genest, and N. Rösch, “Structure and electronic properties of MoVO type mixed-metal oxides - a combined view by experiment and theory.,” Dalton transactions. 2015. link Times cited: 14 Abstract: In this review we address recent efforts from experimental a… read moreAbstract: In this review we address recent efforts from experimental and theoretical side to study MoVO-type mixed metal oxides (MMOs) and their properties. We illustrate how structures of MMOs have been evaluated using a large variety of experimental techniques, such as electron microscopy, neutron diffraction, and X-ray diffraction. Furthermore, we discuss the current view on structure-catalysis correlations, derived from recent experiments. In a second part, we examine useful tools of theoretical chemistry for exploring MoVO-type systems. We discuss the need for using hybrid DFT methods and we analyze how, in the context of MMOs studies, semi-local DFT approximations can encounter problems due to a notable self-interaction error when describing oxidic species and reactions on them. In addition, we discuss various aspects of the model that are important when attempting to map complex MMO systems. read less NOT USED (high confidence) K. L. Joshi, G. Psofogiannakis, A. V. van Duin, and S. Raman, “Reactive molecular simulations of protonation of water clusters and depletion of acidity in H-ZSM-5 zeolite.,” Physical chemistry chemical physics : PCCP. 2014. link Times cited: 40 Abstract: Using reactive molecular dynamics (RMD), we present an atomi… read moreAbstract: Using reactive molecular dynamics (RMD), we present an atomistic insight into the interaction between water molecules and acidic centers of H-ZSM-5 zeolite. The reactive force field method, ReaxFF, was used to evaluate the adsorption and diffusion of water as well as to study the protonation of water molecules inside zeolite channels. The existing Si/Al/O/H parameters were refitted against DFT calculations to improve the ReaxFF description of interaction between water molecules and the acidic sites of zeolites. The diffusion coefficient of water in the zeolite obtained from refitted parameters is in excellent agreement with experimental results. The molecular dynamics (MD) simulations indicate that protonation of water molecules and acidity of the zeolite catalyst depend on water loadings and temperature and the observed trends compare favorably with existing experimental and theoretical studies. At higher water loadings, protonation of water molecules is more frequent leading to formation and growth of protonated water clusters inside zeolite channels. From the analysis of various reaction channels that were observed during the simulations, we found that such water clusters have relatively short life due to frequent interchange of protons and water molecules among the water clusters. Such proton hopping events play a key role in moving the protons between different acidic centers of zeolite. These simulations show the capability of ReaxFF in providing atomistic details of complex chemical interactions between the water phase and solid acid zeolites. read less NOT USED (high confidence) M. Cheng, W. Goddard, and R. Fu, “The Reduction-Coupled Oxo Activation (ROA) Mechanism Responsible for the Catalytic Selective Activation and Functionalization of n-Butane to Maleic Anhydride by Vanadium Phosphate Oxide,” Topics in Catalysis. 2014. link Times cited: 35 NOT USED (high confidence) E. Neyts and A. Bogaerts, “Understanding plasma catalysis through modelling and simulation—a review,” Journal of Physics D: Applied Physics. 2014. link Times cited: 244 Abstract: Plasma catalysis holds great promise for environmental appli… read moreAbstract: Plasma catalysis holds great promise for environmental applications, provided that the process viability can be maximized in terms of energy efficiency and product selectivity. This requires a fundamental understanding of the various processes taking place and especially the mutual interactions between plasma and catalyst. In this review, we therefore first examine the various effects of the plasma on the catalyst and of the catalyst on the plasma that have been described in the literature. Most of these studies are purely experimental. The urgently needed fundamental understanding of the mechanisms underpinning plasma catalysis, however, may also be obtained through modelling and simulation. Therefore, we also provide here an overview of the modelling efforts that have been developed already, on both the atomistic and the macroscale, and we identify the data that can be obtained with these models to illustrate how modelling and simulation may contribute to this field. Last but not least, we also identify future modelling opportunities to obtain a more complete understanding of the various underlying plasma catalytic effects, which is needed to provide a comprehensive picture of plasma catalysis. read less NOT USED (high confidence) B. Ward and R. B. Getman, “Molecular simulations of physical and chemical adsorption under gas and liquid environments using force field- and quantum mechanics-based methods,” Molecular Simulation. 2014. link Times cited: 9 Abstract: Here we review our simulations of adsorption on metal–organi… read moreAbstract: Here we review our simulations of adsorption on metal–organic frameworks (MOFs) and platinum (Pt) catalysts, focusing on the modelling methods required to understand these two very different systems. MOFs are porous, crystalline materials with large surface areas, which are promising for a variety of adsorption applications. We review our simulations of gas uptake in PCN-53 (porous coordination network) as well as gas storage in MOFs functionalised with metal alkoxide sites. While fluid–solid interactions in both systems can be modelled quite well using algebraic force fields, the alkoxide sites in the functionalised MOFs require specialised versions, in order to describe the stronger adsorption energies. We discuss grand canonical Monte Carlo (GCMC) simulations of both systems. Pt is a common catalyst, and simulations have proven quite useful for providing molecular level details to understand its functionality. This involves understanding adsorption phenomena, which often requires quantum mechanical calculations. We describe our periodic boundary condition density functional theory (DFT) simulations of Pt-catalysed NO oxidation, focusing on adsorbate geometries and coverage effects. Finally, we describe one of the current ‘grand challenges’ in molecular simulations of adsorption, modelling catalytic activity in aqueous phase, which requires a combination of algebraic force fields, DFT and GCMC. read less NOT USED (high confidence) M. Yan et al., “Nanowire templated semihollow bicontinuous graphene scrolls: designed construction, mechanism, and enhanced energy storage performance.,” Journal of the American Chemical Society. 2013. link Times cited: 175 Abstract: Graphene scrolls have been widely investigated for applicati… read moreAbstract: Graphene scrolls have been widely investigated for applications in electronics, sensors, energy storage, etc. However, graphene scrolls with tens of micrometers in length and with other materials in their cavities have not been obtained. Here nanowire templated semihollow bicontinuous graphene scroll architecture is designed and constructed through "oriented assembly" and "self-scroll" strategy. These obtained nanowire templated graphene scrolls can achieve over 30 μm in length with interior cavities between the nanowire and scroll. It is demonstrated through experiments and molecular dynamic simulations that the semihollow bicontinuous structure construction processes depend on the systemic energy, the curvature of nanowires, and the reaction time. Lithium batteries based on V3O7 nanowire templated graphene scrolls (VGSs) exhibit an optimal performance with specific capacity of 321 mAh/g at 100 mA/g and 87.3% capacity retention after 400 cycles at 2000 mA/g. The VGS also shows a high conductivity of 1056 S/m and high capacity of 162 mAh/g at a large density of 3000 mA/g with only 5 wt % graphene added which are 27 and 4.5 times as high as those of V3O7 nanowires, respectively. A supercapacitor made of MnO2 nanowire templated graphene scrolls (MGSs) also shows a high capacity of 317 F/g at 1A/g, which is over 1.5 times than that of MnO2 nanowires without graphene scrolls. These excellent energy storage capacities and cycling performance are attributed to the unique structure of the nanowire templated graphene scroll, which provides continuous electron and ion transfer channels and space for free volume expansion of nanowires during cycling. This strategy and understanding can be used to synthesize other nanowire templated graphene scroll architectures, which can be extended to other fabrication processes and fields. read less NOT USED (high confidence) L. Huang, M. Seredych, T. Bandosz, A. V. van Duin, X. Lu, and K. Gubbins, “Controllable atomistic graphene oxide model and its application in hydrogen sulfide removal.,” The Journal of chemical physics. 2013. link Times cited: 22 Abstract: The determination of an atomistic graphene oxide (GO) model … read moreAbstract: The determination of an atomistic graphene oxide (GO) model has been challenging due to the structural dependence on different synthesis methods. In this work we combine temperature-programmed molecular dynamics simulation techniques and the ReaxFF reactive force field to generate realistic atomistic GO structures. By grafting a mixture of epoxy and hydroxyl groups to the basal graphene surface and fine-tuning their initial concentrations, we produce in a controllable manner the GO structures with different functional groups and defects. The models agree with structural experimental data and with other ab initio quantum calculations. Using the generated atomistic models, we perform reactive adsorption calculations for H2S and H2O∕H2S mixtures on GO materials and compare the results with experiment. We find that H2S molecules dissociate on the carbonyl functional groups, and H2O, CO2, and CO molecules are released as reaction products from the GO surface. The calculation reveals that for the H2O∕H2S mixtures, H2O molecules are preferentially adsorbed to the carbonyl sites and block the potential active sites for H2S decomposition. The calculation agrees well with the experiments. The methodology and the procedure applied in this work open a new door to the theoretical studies of GO and can be extended to the research on other amorphous materials. read less NOT USED (high confidence) K. L. Joshi, S. Raman, and A. Duin, “Connectivity-Based Parallel Replica Dynamics for Chemically Reactive Systems: From Femtoseconds to Microseconds,” Journal of Physical Chemistry Letters. 2013. link Times cited: 57 Abstract: Reactive force field methods such as AIREBO, ReaxFF and COMB… read moreAbstract: Reactive force field methods such as AIREBO, ReaxFF and COMB, are extremely useful for studying physical and chemical interactions between molecules and materials. However, many chemical reactions have relatively high activation energies, putting them beyond the times-scale of conventional molecular dynamics (MD) at modest temperatures. To capture the low-temperature long-lived radical chemistry in atomistic simulations, we have developed a new transition detection scheme for performing Reactive Parallel Replica Dynamics (RPRD) simulation enabling an extended MD time-scales, essentially up to a microsecond using ReaxFF. In the newly implemented event detection scheme, the transition events are identified whenever there is a change in connectivity of any atom. 1-Heptene pyrolysis is chosen as a model system, and RPRD simulations are performed at temperatures as low as 1350K for up to 1 μs for a system consisting of 40 heptene molecules. The chemical mechanism and the product distribution that were obtained... read less NOT USED (high confidence) H. Larsson, A. Duin, and B. Hartke, “Global optimization of parameters in the reactive force field ReaxFF for SiOH,” Journal of Computational Chemistry. 2013. link Times cited: 78 Abstract: We have used unbiased global optimization to fit a reactive … read moreAbstract: We have used unbiased global optimization to fit a reactive force field to a given set of reference data. Specifically, we have employed genetic algorithms (GA) to fit ReaxFF to SiOH data, using an in‐house GA code that is parallelized across reference data items via the message‐passing interface (MPI). Details of GA tuning turn‐ed out to be far less important for global optimization efficiency than using suitable ranges within which the parameters are varied. To establish these ranges, either prior knowledge can be used or successive stages of GA optimizations, each building upon the best parameter vectors and ranges found in the previous stage. We have finally arrive‐ed at optimized force fields with smaller error measures than those published previously. Hence, this optimization approach will contribute to converting force‐field fitting from a specialist task to an everyday commodity, even for the more difficult case of reactive force fields. © 2013 Wiley Periodicals, Inc. read less NOT USED (high confidence) O. Verners, Y. Shin, and A. Duin, “Molecular dynamics simulation of Al grain mixing in Fe/Ni matrices and its influence on oxidation,” Journal of Applied Physics. 2013. link Times cited: 1 Abstract: AlxNiyFe(1−x−y) alloys are structural materials with potenti… read moreAbstract: AlxNiyFe(1−x−y) alloys are structural materials with potential application in high-temperature oxidizing environments. These materials are of specific interest as they have the ability to develop an oxidation resistant surface layer. To study diffusion and oxidation processes related to this surface layer formation, the mixing behavior of different sized Al grains in pure Ni and Fe matrices, with approximate grain/matrix atom ratio of 1:3, at temperatures above and below the structure melting point, was studied using ReaxFF-based molecular dynamics simulations. The simulations have been carried out at constant pressure, with temperatures being stepwise ramped over the range of 300-3000 K. For the Ni matrix, our results indicated lower chemical strain energy for Al in the mixed alloy and completion of mixing at a lower temperature for the Fe matrix. These results confirm that the Al-Ni alloy is energetically more stable than the Al-Fe alloy, which is in agreement with experiment. Further, larger Al grains ... read less NOT USED (high confidence) M. Zheng, X. Li, and L. Guo, “Algorithms of GPU-enabled reactive force field (ReaxFF) molecular dynamics.,” Journal of molecular graphics & modelling. 2013. link Times cited: 80 NOT USED (high confidence) K. L. Joshi and A. Duin, “Molecular Dynamics Study on the Influence of Additives on the High-Temperature Structural and Acidic Properties of ZSM-5 Zeolite,” Energy & Fuels. 2013. link Times cited: 14 Abstract: The ReaxFF reactive force field method was used to study the… read moreAbstract: The ReaxFF reactive force field method was used to study the effect of various dopants on the thermal stability and melting process of the zeolites. The force field parameters were fitted against quantum mechanical data for Si/Al/Fe/O/H interactions. Molecular dynamics (MD) simulations were performed using an isothermal–isobaric (NPT) ensemble to investigate the thermal stability of different zeolite frameworks. The zeolite frameworks simulated consisted of silicalite, Al-doped HZSM-5, Fe-doped ZSM5, hydrated ZSM5, and Al- and Fe-doped hydrated HZSM-5. The Lindemann index was used to characterize the melting process. MD results indicate that most of the zeolite frameworks remain stable until 3500 K on the nanosecond time scales accessible to MD simulations. Above 3500 K, the frameworks start to collapse inward, indicating the loss of porous channels. The melting process is initiated due to the disruption of the Si–O–Si network. The presence of water weakens this network due to the hydrogen transfer from w... read less NOT USED (high confidence) S. Naserifar, L. Liu, W. Goddard, T. Tsotsis, and M. Sahimi, “Toward a Process-Based Molecular Model of SiC Membranes. 1. Development of a Reactive Force Field,” Journal of Physical Chemistry C. 2013. link Times cited: 38 Abstract: A broad class of important materials, such as carbon molecul… read moreAbstract: A broad class of important materials, such as carbon molecular sieves, silicon carbide (SiC), and silicon nitride, are fabricated by temperature-controlled pyrolysis of preceramic polymers. In particular, the fabrication of SiC membranes by pyrolysis of a polymer precursor that contains Si is quite attractive for separation of hydrogen from other gases. It has been quite difficult to extract atomistic-scale information about such SiC membranes since they are amorphous. In principle, ab initio quantum mechanics (QM) can provide information about the structure of the amorphous systems. However, to determine the structure of the SiC membrane layer one should capture in the simulations the various reactive processes involved in forming the layer. This requires QM simulations on systems with about 3000 atoms per cell at temperature of 1200 K for microseconds, which are far beyond the current QM capabilities. Instead, this paper extends the ReaxFF reactive force field, validated for high temperature reactions of other materials, to describe the processes involved in the thermal decomposition of hydridopolycarbosilane (HPCS) to form SiC nanoporous membranes. First, we carry out QM calculations on models meant to capture important reaction steps and structures. Then, we develop a model of the HPCS polymer and utilize ReaxFF to describe the thermal degradation and decomposition of the polymer as the system is heated in the molecular dynamics (MD) simulations. Analysis of the pyrolysis studies and their results leads to various quantities that can be compared with experimental data. Good agreement is found between the data and the results of the MD simulations. read less NOT USED (high confidence) Y. Shin, H. Kwak, C. Zou, A. Vasenkov, and A. V. van Duin, “Development and validation of a ReaxFF reactive force field for Fe/Al/Ni alloys: molecular dynamics study of elastic constants, diffusion, and segregation.,” The journal of physical chemistry. A. 2012. link Times cited: 59 Abstract: We have developed a ReaxFF force field for Fe/Al/Ni binary a… read moreAbstract: We have developed a ReaxFF force field for Fe/Al/Ni binary alloys based on quantum mechanical (QM) calculations. In addition to the various bulk phases of the binary alloys, the (100), (110) and (111) surface energies and adatom binding energies were included in the training set for the force field parametrization of the Fe/Al/Ni binary alloys. To validate these optimized force fields, we studied (i) elastic constants of the binary alloys at finite temperatures, (ii) diffusivity of alloy components in Al/Ni alloy, and (iii) segregation on the binary alloy surfaces. First, we calculated linear elastic constants of FeAl, FeNi(3), and Ni(3)Al in the temperature range 300 to 1100 K. The temperature dependences of the elastic constants of these three alloys, showing a decrease in C(11), C(12), and C(44) as temperature increases, were in good agreement with the experimental results. We also performed ReaxFF molecular dynamics (MD) simulations for Al or Ni diffusion in the system modeled as Al/Ni mixed layers with the linear composition gradients. At 1000 K, Al diffusivity at the pure Al end was 2 orders of magnitude larger than that in the Al trace layers, probably explaining the nature of different diffusion behavior between molten metals and alloys. However, the diffusivity of Ni at the pure Ni end was only slightly larger than that in the Ni trace layers at the system temperature much lower than the melting temperature of Ni. Third, we investigated the surface segregation in L1(2)-Fe(3)Al, Fe(3)Ni, and Ni(3)Al clusters at high temperature (2500 K). From the analysis of composition distribution of the alloy components from the bulk to the surface layer, it was found that the degree of segregation depended on the chemical composition of the alloy. Al surface segregation occurred most strongly in Fe(3)Al, whereas it occurred most weakly in Ni(3)Al. These results may support the segregation mechanism that surface segregation results from the interplay between the energetic stability of the ordered bulk phase and the surface reconstruction. In addition, the surface segregation induced the depletion layers of segregating metal species (Al in Fe(3)Al and Ni(3)Al, and Ni in Fe(3)Ni) next to the segregation layers. These simulation results qualitatively agreed with early experimental observations of segregation in Fe/Al/Ni binary alloys. read less NOT USED (high confidence) Y. Shin et al., “Variable charge many-body interatomic potentials,” MRS Bulletin. 2012. link Times cited: 56 Abstract: Recent developments in reactive potentials for the simulatio… read moreAbstract: Recent developments in reactive potentials for the simulation of complex bonding and complex chemistry are reviewed. In particular, the reactive force field and charged optimized many-body methods are two paradigms that enable atoms to autonomously determine their charge state and the nature of their local bonding environments. The capabilities of these methods are illustrated by examples involving ionic-covalent systems, a metal-covalent system, a high- k dielectric gate stack, and the interaction of water with an oxide. Prospects for future development and applications are also discussed. read less NOT USED (high confidence) L. Liu, A. Jaramillo-Botero, W. Goddard, and H. Sun, “Development of a ReaxFF reactive force field for ettringite and study of its mechanical failure modes from reactive dynamics simulations.,” The journal of physical chemistry. A. 2012. link Times cited: 81 Abstract: Ettringite is a hexacalcium aluminate trisulfate hydrate min… read moreAbstract: Ettringite is a hexacalcium aluminate trisulfate hydrate mineral that forms during Portland cement hydration. Its presence plays an important role in controlling the setting rate of the highly reactive aluminate phases in cement paste and has also been associated with severe cracking in cured hardened cement. To understand how it forms and how its properties influence those of hardened cement and concrete, we have developed a first-principles-based ReaxFF reactive force field for Ca/Al/H/O/S. Here, we report on the development of this ReaxFF force field and on its validation and application using reactive molecular dynamics (RMD) simulations to characterize and understand the elastic, plastic, and failure response of ettringite at the atomic scale. The ReaxFF force field was validated by comparing the lattice parameters, pairwise distribution functions, and elastic constants of an ettringite crystal model obtained from RMD simulations with those from experiments. The predicted results are in close agreement with published experimental data. To characterize the atomistic failure modes of ettringite, we performed stress-strain simulations to find that Ca-O bonds are responsible for failure of the calcium sulfate and tricalcium aluminate (C3A) column in ettringite during uniaxial compression and tension and that hydrogen bond re-formation during compression induces an increase in plastic strain beyond the material's stress-strain proportionality limit. These results provide essential insight into understanding the mechanistic role of this mineral in cement and concrete degradation, and the ReaxFF potential developed in this work serves as a fundamental tool to further study the kinetics of hydration in cement and concrete. read less NOT USED (high confidence) S. Kumar, K. Joshi, A. V. van Duin, and M. Haque, “Can amorphization take place in nanoscale interconnects?,” Nanotechnology. 2012. link Times cited: 7 Abstract: The trend of miniaturization has highlighted the problems of… read moreAbstract: The trend of miniaturization has highlighted the problems of heat dissipation and electromigration in nanoelectronic device interconnects, but not amorphization. While amorphization is known to be a high pressure and/or temperature phenomenon, we argue that defect density is the key factor, while temperature and pressure are only the means. For nanoscale interconnects carrying modest current density, large vacancy concentrations may be generated without the necessity of high temperature or pressure due to the large fraction of grain boundaries and triple points. To investigate this hypothesis, we performed in situ transmission electron microscope (TEM) experiments on 200 nm thick (80 nm average grain size) aluminum specimens. Electron diffraction patterns indicate partial amorphization at modest current density of about 105 A cm−2, which is too low to trigger electromigration. Since amorphization results in drastic decrease in mechanical ductility as well as electrical and thermal conductivity, further increase in current density to about 7 × 105 A cm−2 resulted in brittle fracture failure. Our molecular dynamics (MD) simulations predict the formation of amorphous regions in response to large mechanical stresses (due to nanoscale grain size) and excess vacancies at the cathode side of the thin films. The findings of this study suggest that amorphization can precede electromigration and thereby play a vital role in the reliability of micro/nanoelectronic devices. read less NOT USED (high confidence) B. Chen et al., “ReaxFF Reactive Force Field for Molecular Dynamics Simulations of Lignite Depolymerization in Supercritical Methanol with Lignite-Related Model Compounds,” Energy & Fuels. 2012. link Times cited: 34 Abstract: To investigate the detailed mechanisms for lignite methanoly… read moreAbstract: To investigate the detailed mechanisms for lignite methanolysis, we used ReaxFF reactive force field to perform a series of molecular dynamics simulations (MDSs) on a unimolecular model compound. The α-O-4 and β-O-4 types of lignite-related model compounds were selected as representatives of linkages in lignites. The reaction products predicted by ReaxFF MDSs are consistent with those from experimental results reported. The initiation reaction observed in ReaxFF MDSs involving the ether linkage cleavage and methanol participation closely matches the results observed from previously reported experiments. The agreement of these results with available experimental observations demonstrates that ReaxFF MDSs can give an atomistic description of the initiation mechanism for methanolysis and provide useful insights into the complicated reaction processes. read less NOT USED (high confidence) B. Devine et al., “Atomistic simulations of copper oxidation and Cu/Cu2O interfaces using charge-optimized many-body potentials,” Physical Review B. 2011. link Times cited: 64 Abstract: Bryce Devine,1 Tzu-Ray Shan( ),1 Yu-Ting Cheng( ),1 Alan J. … read moreAbstract: Bryce Devine,1 Tzu-Ray Shan( ),1 Yu-Ting Cheng( ),1 Alan J. H. McGaughey,1,2 Minyoung Lee,2 Simon R. Phillpot,1 and Susan B. Sinnott1,* 1Department of Materials Science and Engineering, University of Florida, Gainesville, FL 32611-6400, USA 2Department of Mechanical Engineering, Carnegie-Mellon University, Pittsburgh, PA, 15213, USA (Received 14 February 2011; revised manuscript received 21 July 2011; published 12 September 2011) read less NOT USED (high confidence) W. Goddard, L. Liu, J. Mueller, S. Pudar, and R. J. Nielsen, “Structures, Mechanisms, and Kinetics of Ammoxidation and Selective Oxidation of Propane Over the M2 Phase of MoVNbTeO Catalysts,” Topics in Catalysis. 2011. link Times cited: 19 NOT USED (high confidence) K. L. Joshi, A. Duin, and T. Jacob, “Development of a ReaxFF description of gold oxides and initial application to cold welding of partially oxidized gold surfaces,” Journal of Materials Chemistry. 2010. link Times cited: 30 Abstract: We present the ReaxFF reactive force field methodology for m… read moreAbstract: We present the ReaxFF reactive force field methodology for modeling a gold–oxygen binary system. The force field parameters were fitted against a data set including equations of state, heats of formation and binding energies derived from DFT calculations. The trained force field was then used to study the diffusion properties of oxygen on a gold surface. The diffusion study shows that oxygen atoms have a relatively low mobility on the gold surface. We also present a prospective application of this force field by performing molecular dynamics simulations studying the effect of oxidation level on contact strength of a cold welded joint. The results indicate that low levels of oxidation can significantly impact the joint cohesive energy. read less NOT USED (high confidence) D. Raymand, A. Duin, D. Spångberg, W. Goddard, and K. Hermansson, “Water adsorption on stepped ZnO surfaces from MD simulation,” Surface Science. 2010. link Times cited: 135 NOT USED (high confidence) J. Mueller, A. Duin, and W. Goddard, “Development and Validation of ReaxFF Reactive Force Field for Hydrocarbon Chemistry Catalyzed by Nickel,” Journal of Physical Chemistry C. 2010. link Times cited: 285 Abstract: To enable the study of hydrocarbon reactions catalyzed by ni… read moreAbstract: To enable the study of hydrocarbon reactions catalyzed by nickel surfaces and particles using reactive molecular dynamics on thousands of atoms as a function of temperature and pressure, we have developed the ReaxFF reactive force field to describe adsorption, decomposition, reformation and desorption of hydrocarbons as they interact with the nickel surface. The ReaxFF parameters were determined by fitting to the geometries and energy surfaces from quantum mechanics (QM) calculations for a large number of reaction pathways for hydrocarbon molecules chemisorbed onto nickel (111), (100) and (110) surfaces, supplemented with QM equations of state for nickel and nickel carbides. We demonstrate the validity and accuracy of ReaxFF by applying it to study the reaction dynamics of hydrocarbons as catalyzed by nickel particles and surfaces. For the dissociation of methyl on the (111), (100), and stepped (111) surfaces of nickel, we observe the formation of chemisorbed CH plus subsurface carbide. We observe that th... read less NOT USED (high confidence) L. Sun and W. Deng, “Recent developments of first‐principles force fields,” Wiley Interdisciplinary Reviews: Computational Molecular Science. 2017. link Times cited: 18 Abstract: Molecular mechanics force fields derived from first‐principl… read moreAbstract: Molecular mechanics force fields derived from first‐principles calculations represent the next generation of force fields for molecular dynamics simulations. In recent years, a large amount of first‐principles force fields have been developed in the fields of physical and biological fields. Here, we review the first‐principles force fields especially for simulating the adsorption of small molecules in nanoporous materials and on surfaces. We describe the latest developments in force field parameterization and application, primarily in the last 10 years. Emphasis is placed on the procedure in developing these first‐principles force fields. We discuss the selections of first‐principles methods and fragment models during the parameterization. As the first‐principles force fields are available in a wide range of simulation packages, it is anticipated that use of these force fields will lead to new discoveries of the adsorption phenomena in nanoporous materials and on surfaces. WIREs Comput Mol Sci 2017, 7:e1282. doi: 10.1002/wcms.1282 read less NOT USED (high confidence) P. Song, Y. Ding, and D. Wen, “A reactive molecular dynamic simulation of oxidation of a silicon nanocluster,” Journal of Nanoparticle Research. 2012. link Times cited: 6 NOT USED (high confidence) F. Keil, “Multiscale modelling in computational heterogeneous catalysis.,” Topics in current chemistry. 2012. link Times cited: 54 |